7.4.1 二项分布 教学课件(共38张PPT)高中数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.4.1 二项分布 教学课件(共38张PPT)高中数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 56.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 12:53:01 | ||
图片预览










文档简介
(共38张PPT)
7.4.1 二项分布
人教A版(2019)选择性必修三
素养目标
1.通过具体实例,了解伯努利试验与n重伯努利试验,提升逻辑推理能力(重点)
2. 掌握二项分布及其数字特征,并能解决简单的实际问题,提升数学运算能力(难点)
新课导入
考虑下面的事件:
(1)抛掷一枚质地均匀的硬币10次.
(2)某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.
(3)一批产品的次品率为 5%, 有放回地随机抽取20件.
这些事件有什么相同的特征?
新课学习
伯努利试验的概念
在实际问题中, 有许多随机试验与郑硬币试验具有相同的特征, 它们只包含两个可能结果. 例如,检验一件产品结果为合格或不合格,飞碟射击时中靶或脱靶,医学检验结果为阳性或阴性等. 我们把只包含两个可能结果的试验叫做伯努利试验.
新课学习
n重伯努利试验的概念
将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验.显然,n重伯努利试验具有如下共同特征:
(1)同一个伯努利试验重复做n次;
(2)各次试验的结果相互独立.
重复意味着各次试验成功的概念相同
新课学习
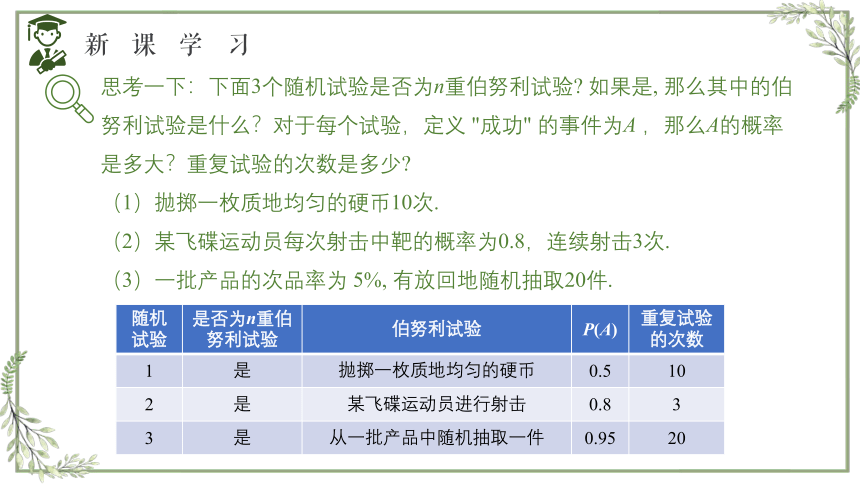
思考一下:下面3个随机试验是否为n重伯努利试验 如果是, 那么其中的伯努利试验是什么?对于每个试验,定义 "成功" 的事件为A ,那么A的概率是多大?重复试验的次数是多少
(1)抛掷一枚质地均匀的硬币10次.
(2)某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.
(3)一批产品的次品率为 5%, 有放回地随机抽取20件.
随机试验 是否为n重伯努利试验 伯努利试验 P(A) 重复试验的次数
1 是 抛掷一枚质地均匀的硬币 0.5 10
2 是 某飞碟运动员进行射击 0.8 3
3 是 从一批产品中随机抽取一件 0.95 20
新课学习
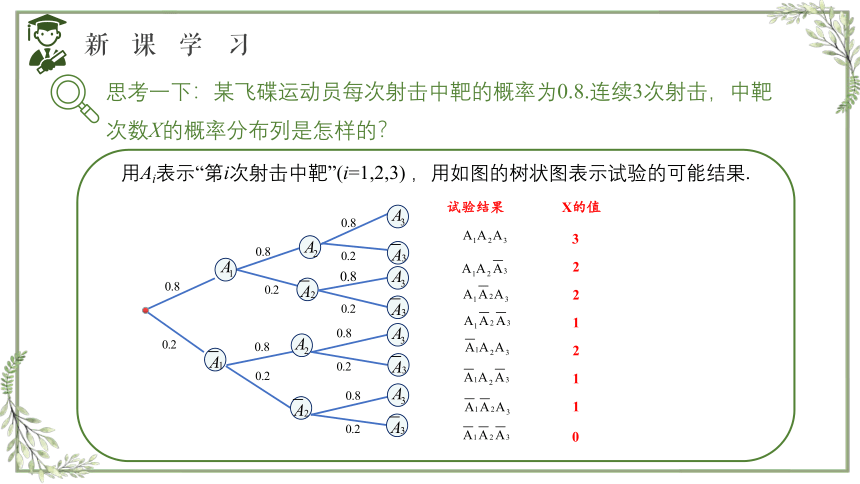
思考一下:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数X的概率分布列是怎样的?
用Ai表示“第i次射击中靶”(i=1,2,3) ,用如图的树状图表示试验的可能结果.
3
2
2
1
2
1
1
0
试验结果 X的值
新课学习
由分步乘法计数原理,3次独立重复试验共有23=8种可能结果,它们两两互斥,每个结果都是3个相互独立事件的积.由概率的加法公式和乘法公式得
思考一下:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数X的概率分布列是怎样的?
新课学习
思考一下:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数X的概率分布列是怎样的?
为了简化表示,每次射击用1表示中靶,用0表示脱靶,那么3次射击恰好2次中靶的所有可能结果可表示为011,110,101,这三个结果发生的概率都相等,均为0.82×0.2,并且与哪两次中靶无关.
新课学习
思考一下:如果连续射击 4 次, 类比上面的分析, 表示中靶次数X等于 2 的结果有哪些 写出中靶次数X的分布列?
表示中靶次数X等于2的结果有:
中靶次数X的分布列为
新课学习
二项分布的概念
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0如果随机变量X的分布列具有上式的形式,则称随机变量X服从二项分布,记作X~B(n,p) .
由二项式定理,容易得到
新课学习
例1 将一枚质地均匀的硬币重复抛掷10次,求:
(1)恰好出现5次正面朝上的概率;
分析:抛掷一枚质地均匀的硬币,出现“正面朝上”和“反面朝上”两种结果且可能性相等,这是一个10重伯努利试验.因此,正面朝上的次数服从二项分布.
设A= “正面朝上”,则P(A)=0.5.用X表示事件A发生的次数,则X~B(10,0.5) .
恰好出现5次正面朝上等价于X=5 ,于是
新课学习
(2)正面朝上出现的频率在[0.4,0.6]内的概率.
新课学习
例2 图中是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃.将小球从顶端放入,小球下落的过程中,每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中.格子从左到右分别编号为0,1,2,..,10,用X表示小球最后落入格子的号码,求X的分布列.
分析:小球落入哪个格子取决于在下落过程中与各小木钉碰撞的结果.设试验为观察小球碰到小木钉后下落的方向,有“向左下落”和“向右下落”两种可能结果,且概率都是0.5.在下落的过程中,小球共碰撞小木钉10次,且每次碰撞后下落方向不受上一次下落方向的影响,因此这是一个10重伯努利试验.小球最后落入格子的号码等于向右落下的次数,因此X服从二项分布.
新课学习
设A=”向右下落”,则=“向左下落”,则P(A)=P()=0.5.
因为小球最后落入格子的号码X等于事件A发生的次数,而小球在下落的过程中共碰撞小木钉10次,所以X~B(10,0.5),于是X的分布列为
X的概率分布图如图所示:
新课学习
例3 甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利?
分析:判断哪个赛制对甲有利,就是看在哪个赛制中甲最终获胜的概率大.可以把“甲最终获胜”这个事件,按可能的比分情况表示为若干事件的和,再利用各局比赛结果的独立性逐个求概率;也可以假定赛完所有n局,把n局比赛看成n重伯努利试验,利用二项分布求“甲最终获胜”的概率.
新课学习
解法一:采用3局2胜制,甲最终获胜有两种可能的比分2:0或2:1,前者是前两局甲连胜,后者是前两局甲、乙各胜一局且第3局甲胜.因为每局比赛的结果是独立的,甲最终获胜的概率为
类似地,采用5局3胜制,甲最终获胜有3种比分3:0,3:1或3:2 .因为每局比赛的结果是独立的,所以甲最终获胜的概率为
新课学习
解法二:采用3局2胜制,不妨设赛满3局,用X表示3局比赛中甲胜的局数,则 X~B(3,0.6). 甲最终获胜的概率为
采用 5局3胜制,不妨设赛满5局,用 X 表示5局比赛中甲胜的局数, 则X~B(5,0.6). 甲最终获胜的概率为
因为 p2>p1, 所以5局3胜制对甲有利. 实际上, 比赛局数越多, 对实力较强者越有利.
新课学习
思考一下:为什么假定赛满3局或5局,不满足甲最终获胜的概率?
从比分上看: 3 局 2 胜的比分应为2:0 或2:1, 对 " 2:0 ", 若设赛满3局, 则第3局甲无论胜、负总体都是甲胜, 故这个 " 2:0 " 可分为 " 3:0 " 与 "2: 1" 两种情况; 对 " 2:1 "本身就赛满 3 局, 故p1=P(X=2)+P(X =3).
从甲获胜对应的概率值上看: 2:0对应概率 0.62=(0.6+0.4) ×0.62=0.63+0.62×0.4,
2:1 对应概率为
对5局3胜可定赛满5局与此类似.
新课学习
归纳:一般地,确定一个二项分布模型的步骤如下:
1.明确伯努利试验及事件A的意义,确定事件A发生的概率p;
2.确定重复试验的次数n,并判断各次试验的独立性;
3.设X为n次独立重复试验中事件A发生的次数,则X~B(n,p) .
新课学习
思考一下:假设随机变量X服从二项分布B(n,p),那么X的均值和方差各是什么?
我们知道,抛掷一枚质地均匀的硬币,“正面朝上”的概率为0.5,如果掷100次硬币,期望有100×0.5=50次正面朝上.根据均值的含义,对于服从二项分布的随机变量X,我们猜想E(X) =np.
先考察n较小的情况.
(1)当n=1时,X服从两点分布,分布列为 P(X=0)=1-p,P(X=1)=p.均值和方差分别为 E(X)=p,D(X)=p(1-p).
(2)当n=2时,X的分布列为P(X=0)=(1-p)2, P(X=1)=2p(1-p),P(X=2)=p2.均值和方差分别为E(X)=0×(1-p)2+1×2p(1-p)+2×p2=2p,D(X)=02×(1-p)2+12×2p(1-p)+22×p2-(2p)2=2p(1-p).
新课学习
归纳:对均值进行证明:
新课学习
归纳:对方差进行证明:
又
新课学习
归纳:对方差进行证明:
因此 D(X)=n(n-1)p2+np-(np)2=np-np2=np(1-p)
新课学习
思考一下:二项分布在实际问题中有什么应用?
二项分布的应用非常广泛.
例如,生产过程中的质量控制和抽样方案,都是以二项分布为基础的;参加某保险人群中发生保险事故的人数,试制药品治愈某种疾病的人数,感染某种病毒的家禽数等,都可以用二项分布来描述.
课堂巩固
D
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
9
总结一下
1.伯努利试验
2.n重伯努利试验
3.二项分布
4.二项分布的均值与方差
感谢同学们观看
7.4.1 二项分布
人教A版(2019)选择性必修三
素养目标
1.通过具体实例,了解伯努利试验与n重伯努利试验,提升逻辑推理能力(重点)
2. 掌握二项分布及其数字特征,并能解决简单的实际问题,提升数学运算能力(难点)
新课导入
考虑下面的事件:
(1)抛掷一枚质地均匀的硬币10次.
(2)某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.
(3)一批产品的次品率为 5%, 有放回地随机抽取20件.
这些事件有什么相同的特征?
新课学习
伯努利试验的概念
在实际问题中, 有许多随机试验与郑硬币试验具有相同的特征, 它们只包含两个可能结果. 例如,检验一件产品结果为合格或不合格,飞碟射击时中靶或脱靶,医学检验结果为阳性或阴性等. 我们把只包含两个可能结果的试验叫做伯努利试验.
新课学习
n重伯努利试验的概念
将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验.显然,n重伯努利试验具有如下共同特征:
(1)同一个伯努利试验重复做n次;
(2)各次试验的结果相互独立.
重复意味着各次试验成功的概念相同
新课学习
思考一下:下面3个随机试验是否为n重伯努利试验 如果是, 那么其中的伯努利试验是什么?对于每个试验,定义 "成功" 的事件为A ,那么A的概率是多大?重复试验的次数是多少
(1)抛掷一枚质地均匀的硬币10次.
(2)某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.
(3)一批产品的次品率为 5%, 有放回地随机抽取20件.
随机试验 是否为n重伯努利试验 伯努利试验 P(A) 重复试验的次数
1 是 抛掷一枚质地均匀的硬币 0.5 10
2 是 某飞碟运动员进行射击 0.8 3
3 是 从一批产品中随机抽取一件 0.95 20
新课学习
思考一下:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数X的概率分布列是怎样的?
用Ai表示“第i次射击中靶”(i=1,2,3) ,用如图的树状图表示试验的可能结果.
3
2
2
1
2
1
1
0
试验结果 X的值
新课学习
由分步乘法计数原理,3次独立重复试验共有23=8种可能结果,它们两两互斥,每个结果都是3个相互独立事件的积.由概率的加法公式和乘法公式得
思考一下:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数X的概率分布列是怎样的?
新课学习
思考一下:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数X的概率分布列是怎样的?
为了简化表示,每次射击用1表示中靶,用0表示脱靶,那么3次射击恰好2次中靶的所有可能结果可表示为011,110,101,这三个结果发生的概率都相等,均为0.82×0.2,并且与哪两次中靶无关.
新课学习
思考一下:如果连续射击 4 次, 类比上面的分析, 表示中靶次数X等于 2 的结果有哪些 写出中靶次数X的分布列?
表示中靶次数X等于2的结果有:
中靶次数X的分布列为
新课学习
二项分布的概念
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0
由二项式定理,容易得到
新课学习
例1 将一枚质地均匀的硬币重复抛掷10次,求:
(1)恰好出现5次正面朝上的概率;
分析:抛掷一枚质地均匀的硬币,出现“正面朝上”和“反面朝上”两种结果且可能性相等,这是一个10重伯努利试验.因此,正面朝上的次数服从二项分布.
设A= “正面朝上”,则P(A)=0.5.用X表示事件A发生的次数,则X~B(10,0.5) .
恰好出现5次正面朝上等价于X=5 ,于是
新课学习
(2)正面朝上出现的频率在[0.4,0.6]内的概率.
新课学习
例2 图中是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃.将小球从顶端放入,小球下落的过程中,每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中.格子从左到右分别编号为0,1,2,..,10,用X表示小球最后落入格子的号码,求X的分布列.
分析:小球落入哪个格子取决于在下落过程中与各小木钉碰撞的结果.设试验为观察小球碰到小木钉后下落的方向,有“向左下落”和“向右下落”两种可能结果,且概率都是0.5.在下落的过程中,小球共碰撞小木钉10次,且每次碰撞后下落方向不受上一次下落方向的影响,因此这是一个10重伯努利试验.小球最后落入格子的号码等于向右落下的次数,因此X服从二项分布.
新课学习
设A=”向右下落”,则=“向左下落”,则P(A)=P()=0.5.
因为小球最后落入格子的号码X等于事件A发生的次数,而小球在下落的过程中共碰撞小木钉10次,所以X~B(10,0.5),于是X的分布列为
X的概率分布图如图所示:
新课学习
例3 甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利?
分析:判断哪个赛制对甲有利,就是看在哪个赛制中甲最终获胜的概率大.可以把“甲最终获胜”这个事件,按可能的比分情况表示为若干事件的和,再利用各局比赛结果的独立性逐个求概率;也可以假定赛完所有n局,把n局比赛看成n重伯努利试验,利用二项分布求“甲最终获胜”的概率.
新课学习
解法一:采用3局2胜制,甲最终获胜有两种可能的比分2:0或2:1,前者是前两局甲连胜,后者是前两局甲、乙各胜一局且第3局甲胜.因为每局比赛的结果是独立的,甲最终获胜的概率为
类似地,采用5局3胜制,甲最终获胜有3种比分3:0,3:1或3:2 .因为每局比赛的结果是独立的,所以甲最终获胜的概率为
新课学习
解法二:采用3局2胜制,不妨设赛满3局,用X表示3局比赛中甲胜的局数,则 X~B(3,0.6). 甲最终获胜的概率为
采用 5局3胜制,不妨设赛满5局,用 X 表示5局比赛中甲胜的局数, 则X~B(5,0.6). 甲最终获胜的概率为
因为 p2>p1, 所以5局3胜制对甲有利. 实际上, 比赛局数越多, 对实力较强者越有利.
新课学习
思考一下:为什么假定赛满3局或5局,不满足甲最终获胜的概率?
从比分上看: 3 局 2 胜的比分应为2:0 或2:1, 对 " 2:0 ", 若设赛满3局, 则第3局甲无论胜、负总体都是甲胜, 故这个 " 2:0 " 可分为 " 3:0 " 与 "2: 1" 两种情况; 对 " 2:1 "本身就赛满 3 局, 故p1=P(X=2)+P(X =3).
从甲获胜对应的概率值上看: 2:0对应概率 0.62=(0.6+0.4) ×0.62=0.63+0.62×0.4,
2:1 对应概率为
对5局3胜可定赛满5局与此类似.
新课学习
归纳:一般地,确定一个二项分布模型的步骤如下:
1.明确伯努利试验及事件A的意义,确定事件A发生的概率p;
2.确定重复试验的次数n,并判断各次试验的独立性;
3.设X为n次独立重复试验中事件A发生的次数,则X~B(n,p) .
新课学习
思考一下:假设随机变量X服从二项分布B(n,p),那么X的均值和方差各是什么?
我们知道,抛掷一枚质地均匀的硬币,“正面朝上”的概率为0.5,如果掷100次硬币,期望有100×0.5=50次正面朝上.根据均值的含义,对于服从二项分布的随机变量X,我们猜想E(X) =np.
先考察n较小的情况.
(1)当n=1时,X服从两点分布,分布列为 P(X=0)=1-p,P(X=1)=p.均值和方差分别为 E(X)=p,D(X)=p(1-p).
(2)当n=2时,X的分布列为P(X=0)=(1-p)2, P(X=1)=2p(1-p),P(X=2)=p2.均值和方差分别为E(X)=0×(1-p)2+1×2p(1-p)+2×p2=2p,D(X)=02×(1-p)2+12×2p(1-p)+22×p2-(2p)2=2p(1-p).
新课学习
归纳:对均值进行证明:
新课学习
归纳:对方差进行证明:
又
新课学习
归纳:对方差进行证明:
因此 D(X)=n(n-1)p2+np-(np)2=np-np2=np(1-p)
新课学习
思考一下:二项分布在实际问题中有什么应用?
二项分布的应用非常广泛.
例如,生产过程中的质量控制和抽样方案,都是以二项分布为基础的;参加某保险人群中发生保险事故的人数,试制药品治愈某种疾病的人数,感染某种病毒的家禽数等,都可以用二项分布来描述.
课堂巩固
D
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
9
总结一下
1.伯努利试验
2.n重伯努利试验
3.二项分布
4.二项分布的均值与方差
感谢同学们观看
