7.4.2 超几何分布 教学课件(共32张PPT)高中数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.4.2 超几何分布 教学课件(共32张PPT)高中数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 48.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 12:53:23 | ||
图片预览











文档简介
(共32张PPT)
7.4.2 超几何分布
人教A版(2019)选择性必修三
素养目标
1.通过具体实例,了解超几何分布,提升逻辑推理能力
2. 掌握超几何分布及其均值,并能解决简单的实际问题,提升数学运算能力
重点
难点
新课导入
思考一下:已知100件产品中有8件次品,分别采用有放回和不放回的方式随机抽取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列.
如果采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时X服从二项分布,即
X~B(4,0.08)
思考一下:如果采用不放回抽样,那么抽取的4件产品中次品数X是否也服从二项分布?如果不服从,那么X的分布列是什么?
新课学习
采用不放回抽样,虽然每次抽到次品的概率都是0.08,但每次抽取不是同一个试验,而且各次抽取的结果也不独立,不符合n重伯努利试验的特征,因此X不服从二项分布.
新课学习
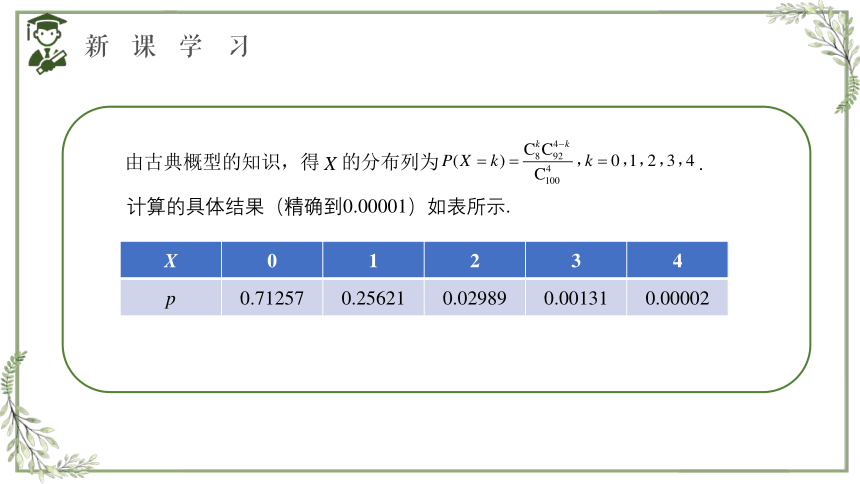
计算的具体结果(精确到0.00001)如表所示.
X 0 1 2 3 4
p 0.71257 0.25621 0.02989 0.00131 0.00002
新课学习
思考一下:计算结果数时, 考虑抽取的次序和不考虑抽取的次序, 对分布列的计算有影响吗 为什么
不影响
因为不考虑抽取次序时
考虑抽取次序时
故是否考虑抽取次序对分布列的计算没有影响.
新课学习
超几何分布的概念
一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为
如果随机变量X的分布列具有上式的形式,那么称随机变量X 服从超几何分布.
新课学习
超几何分布的符号表示
若随机变量 X 服从超几何分布, 则记为 X~H(n,M,N), 并将
记为 H(k;n,M,N) ,其中k 表示样本中的次品数, n 表示样本容量, M 表示次品总数, N表示总体中的个体总数.
新课学习
例1 从50名学生中随机选出5名学生代表,求甲被选中的概率.
设X表示选出的5名学生中含甲的人数(只能取0或1),则X服从超几何分布,且因此甲被选中的概率N=50,M=1,n=5.因此甲被选中的概率为
新课学习
例2 一批零件共有 30 个, 其中有 3 个不合格. 随机抽取 10 个零件进行检测, 求至少有 1 件不合格的概率.
设抽取的 10 个零件中不合格品数为 X, 则 X 服从超几何分布, 且 N=30, M=3, n=10.X 的分布列为
至少有 1 件不合格的概率为
也可以按如下方法求解:
新课学习
探究思考:服从超几何分布的随机变量的均值是什么?
随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,不放回地随机抽取n件产品中的次品数.
新课学习
探究思考:服从超几何分布的随机变量的均值是什么?
因为
所以
新课学习
例3 一个袋子中有100个大小相同的球,其中有40个黄球、60个白球,从中随机地摸出20个球作为样本.用X表示样本中黄球的个数.
(1)分别就有放回摸球和不放回摸球,求X的分布列;
分析:因为只有两种颜色的球,每次摸球都是一个伯努利试验. 摸出 20 个球,采用有放回摸球,各次试验的结果相互独立, X~B(20,0.4) ;而采用不放回摸球,各次试验的结果不独立, X 服从超几何分布.
新课学习
对于有放回摸球,每次摸到黄球的概率为0.4,且各次试验之间的结果是独立的,因此X~B(20,0.4),X的分布列为
对于不放回摸球,各次试验的结果不独立,X服从超几何分布,X的分布列为
新课学习
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差不超过0.1的概率.
利用统计软件可以计算出两个分布列具体的概率值(精确到0.00001),如表所示.
新课学习
样本中黄球的比例 f20= 是一个随机变量,根据表计算得
有放回摸球:
P(|f20-0.4|≤0.1)=P(6≤X≤10)=P(X=6)+P(X=7)+P(X=8)+P(X=9)+P(X=10)≈0.7469
不放回摸球:P(|f20-0.4|≤0.1)=P(6≤X≤10)≈0.7988
因此,在相同的误差限制下,采用不放回摸球估计的结果更可靠些.
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差不超过0.1的概率.
新课学习
思考一下:对于上述问题,超几何分布相比二项分布有什么关系?
两种摸球方式下,随机变量X分别服从二项分布和超几何分布.
虽然这两种分布有相等的均值(都是8),但从两种分布的概率分布图(下图)看,超几何分布更集中在均值附近.
新课学习
思考一下:对于上述问题,超几何分布相比二项分布有什么优点?
二项分布和超几何分布都可以描述随机抽取的n件产品中次品数的分布规律,并且二者的均值相同.对于不放回抽样,当n远远小于N时,每抽取一次后,对N的影响很小,此时,超几何分布可以用二项分布近似.
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
1.5
课堂巩固
总结一下
1.超几何分布的概念
2.超几何分布的符号表示
3.超几何分布的均值
感谢同学们观看
7.4.2 超几何分布
人教A版(2019)选择性必修三
素养目标
1.通过具体实例,了解超几何分布,提升逻辑推理能力
2. 掌握超几何分布及其均值,并能解决简单的实际问题,提升数学运算能力
重点
难点
新课导入
思考一下:已知100件产品中有8件次品,分别采用有放回和不放回的方式随机抽取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列.
如果采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时X服从二项分布,即
X~B(4,0.08)
思考一下:如果采用不放回抽样,那么抽取的4件产品中次品数X是否也服从二项分布?如果不服从,那么X的分布列是什么?
新课学习
采用不放回抽样,虽然每次抽到次品的概率都是0.08,但每次抽取不是同一个试验,而且各次抽取的结果也不独立,不符合n重伯努利试验的特征,因此X不服从二项分布.
新课学习
计算的具体结果(精确到0.00001)如表所示.
X 0 1 2 3 4
p 0.71257 0.25621 0.02989 0.00131 0.00002
新课学习
思考一下:计算结果数时, 考虑抽取的次序和不考虑抽取的次序, 对分布列的计算有影响吗 为什么
不影响
因为不考虑抽取次序时
考虑抽取次序时
故是否考虑抽取次序对分布列的计算没有影响.
新课学习
超几何分布的概念
一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为
如果随机变量X的分布列具有上式的形式,那么称随机变量X 服从超几何分布.
新课学习
超几何分布的符号表示
若随机变量 X 服从超几何分布, 则记为 X~H(n,M,N), 并将
记为 H(k;n,M,N) ,其中k 表示样本中的次品数, n 表示样本容量, M 表示次品总数, N表示总体中的个体总数.
新课学习
例1 从50名学生中随机选出5名学生代表,求甲被选中的概率.
设X表示选出的5名学生中含甲的人数(只能取0或1),则X服从超几何分布,且因此甲被选中的概率N=50,M=1,n=5.因此甲被选中的概率为
新课学习
例2 一批零件共有 30 个, 其中有 3 个不合格. 随机抽取 10 个零件进行检测, 求至少有 1 件不合格的概率.
设抽取的 10 个零件中不合格品数为 X, 则 X 服从超几何分布, 且 N=30, M=3, n=10.X 的分布列为
至少有 1 件不合格的概率为
也可以按如下方法求解:
新课学习
探究思考:服从超几何分布的随机变量的均值是什么?
随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,不放回地随机抽取n件产品中的次品数.
新课学习
探究思考:服从超几何分布的随机变量的均值是什么?
因为
所以
新课学习
例3 一个袋子中有100个大小相同的球,其中有40个黄球、60个白球,从中随机地摸出20个球作为样本.用X表示样本中黄球的个数.
(1)分别就有放回摸球和不放回摸球,求X的分布列;
分析:因为只有两种颜色的球,每次摸球都是一个伯努利试验. 摸出 20 个球,采用有放回摸球,各次试验的结果相互独立, X~B(20,0.4) ;而采用不放回摸球,各次试验的结果不独立, X 服从超几何分布.
新课学习
对于有放回摸球,每次摸到黄球的概率为0.4,且各次试验之间的结果是独立的,因此X~B(20,0.4),X的分布列为
对于不放回摸球,各次试验的结果不独立,X服从超几何分布,X的分布列为
新课学习
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差不超过0.1的概率.
利用统计软件可以计算出两个分布列具体的概率值(精确到0.00001),如表所示.
新课学习
样本中黄球的比例 f20= 是一个随机变量,根据表计算得
有放回摸球:
P(|f20-0.4|≤0.1)=P(6≤X≤10)=P(X=6)+P(X=7)+P(X=8)+P(X=9)+P(X=10)≈0.7469
不放回摸球:P(|f20-0.4|≤0.1)=P(6≤X≤10)≈0.7988
因此,在相同的误差限制下,采用不放回摸球估计的结果更可靠些.
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差不超过0.1的概率.
新课学习
思考一下:对于上述问题,超几何分布相比二项分布有什么关系?
两种摸球方式下,随机变量X分别服从二项分布和超几何分布.
虽然这两种分布有相等的均值(都是8),但从两种分布的概率分布图(下图)看,超几何分布更集中在均值附近.
新课学习
思考一下:对于上述问题,超几何分布相比二项分布有什么优点?
二项分布和超几何分布都可以描述随机抽取的n件产品中次品数的分布规律,并且二者的均值相同.对于不放回抽样,当n远远小于N时,每抽取一次后,对N的影响很小,此时,超几何分布可以用二项分布近似.
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
1.5
课堂巩固
总结一下
1.超几何分布的概念
2.超几何分布的符号表示
3.超几何分布的均值
感谢同学们观看
