8.2 一元线性回归模型及其应用(第二课时) 教学课件(共40张PPT)高中数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 8.2 一元线性回归模型及其应用(第二课时) 教学课件(共40张PPT)高中数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 47.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 12:55:47 | ||
图片预览



文档简介
(共40张PPT)
8.2 一元线性回归模型及其应用
(第二课时)
人教A版(2019)选择性必修三
素养目标
1.针对实际问题,会用一元线性回归模型进行预测,提升逻辑推理能力(重点)
2.通过对具体问题的进一步分析,能将某些非线性回归问题转化为线性回归问题并加以解决,提升数学运算能力(重点)
3.通过具体实例,了解决定系数R2的意义和作用,提升逻辑推理能力(难点)
新课导入
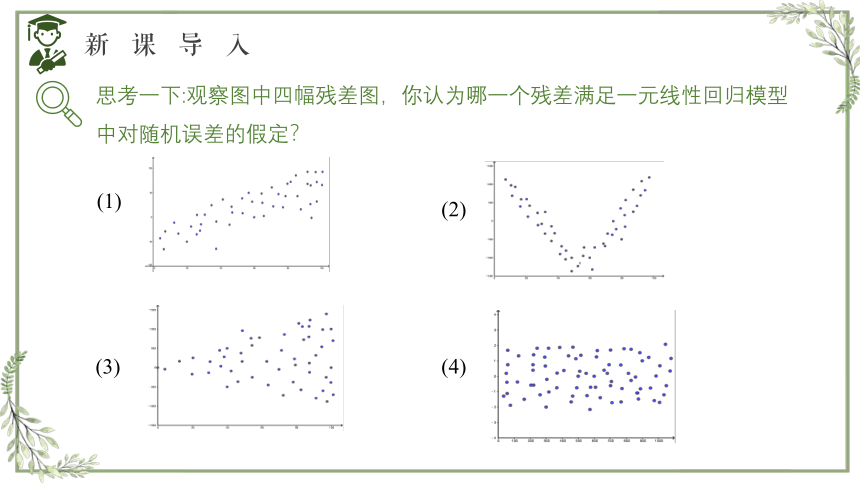
思考一下:观察图中四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定?
(1)
(2)
(3)
(4)
新课学习
根据一元线性回归模型中对随机误差的假定,残差应是均值为0 ,方差为σ2 的随机变量的观测值.
图(1)显示残差与观测时间有线性关系,应将时间变量纳入模型;
图(2)显示残差与观测时间有非线性关系,应在模型中加入时间的非线性函数部分;
图(3)说明残差的方差不是一个常数,随观测时间变大而变大;
图(4)的残差比较均匀地分布在以取值为0的横轴为对称轴的水平带状区域内.
可见,在图中,只有图(4)满足一元线性回归模型对随机误差的假设.
新课学习
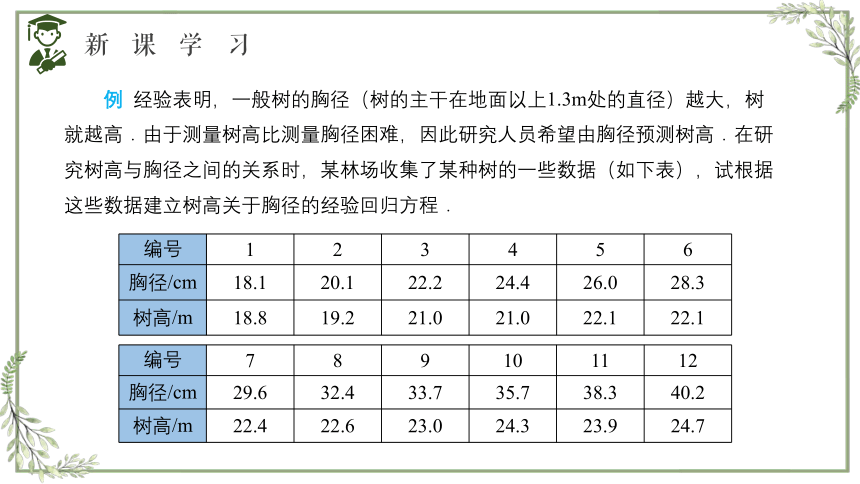
例 经验表明,一般树的胸径(树的主干在地面以上1.3m处的直径)越大,树就越高.由于测量树高比测量胸径困难,因此研究人员希望由胸径预测树高.在研究树高与胸径之间的关系时,某林场收集了某种树的一些数据(如下表),试根据这些数据建立树高关于胸径的经验回归方程.
编号 1 2 3 4 5 6
胸径/cm 18.1 20.1 22.2 24.4 26.0 28.3
树高/m 18.8 19.2 21.0 21.0 22.1 22.1
编号 7 8 9 10 11 12
胸径/cm 29.6 32.4 33.7 35.7 38.3 40.2
树高/m 22.4 22.6 23.0 24.3 23.9 24.7
新课学习
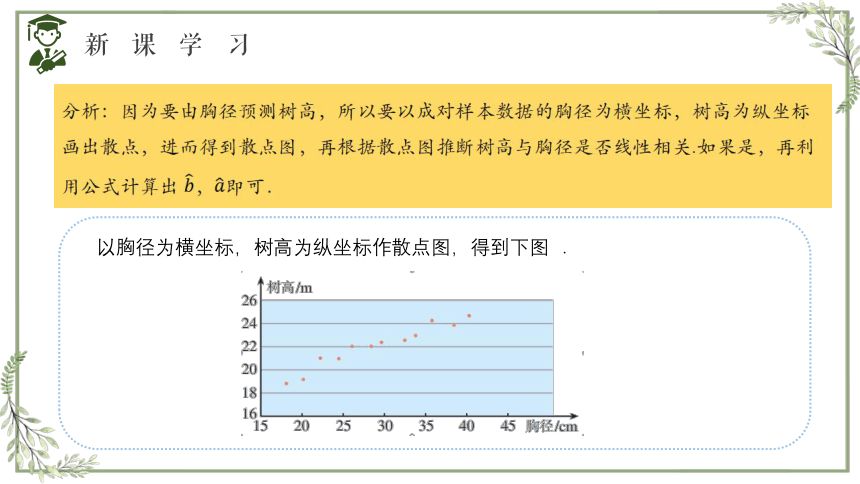
分析:因为要由胸径预测树高,所以要以成对样本数据的胸径为横坐标,树高为纵坐标画出散点,进而得到散点图,再根据散点图推断树高与胸径是否线性相关.如果是,再利用公式计算出 ,即可.
以胸径为横坐标,树高为纵坐标作散点图,得到下图 .
新课学习
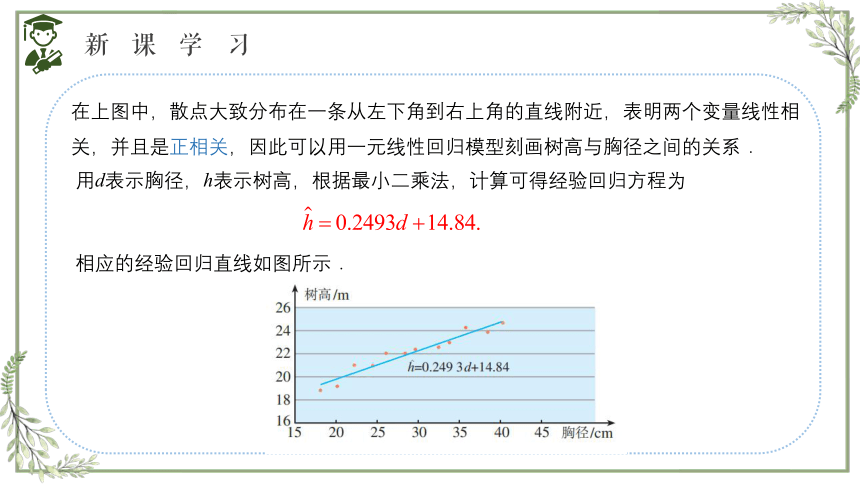
在上图中,散点大致分布在一条从左下角到右上角的直线附近,表明两个变量线性相关,并且是正相关,因此可以用一元线性回归模型刻画树高与胸径之间的关系.
用d表示胸径,h表示树高,根据最小二乘法,计算可得经验回归方程为
相应的经验回归直线如图所示.
新课学习
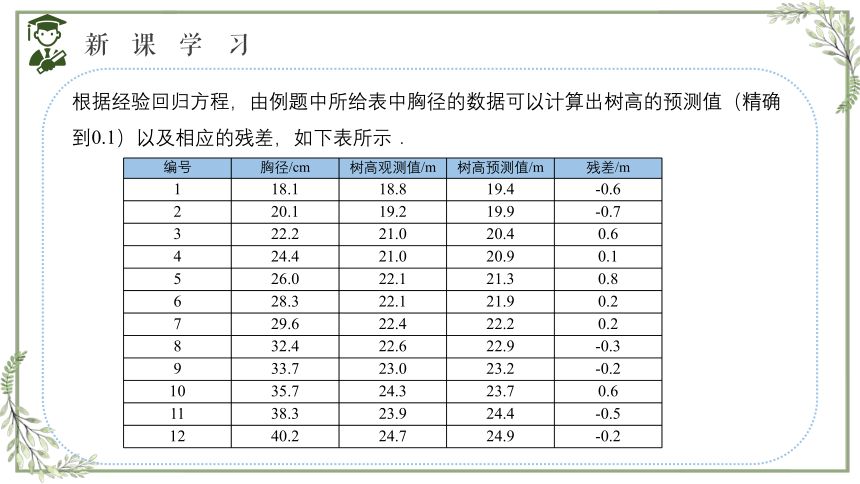
根据经验回归方程,由例题中所给表中胸径的数据可以计算出树高的预测值(精确到0.1)以及相应的残差,如下表所示.
编号 胸径/cm 树高观测值/m 树高预测值/m 残差/m
1 18.1 18.8 19.4 -0.6
2 20.1 19.2 19.9 -0.7
3 22.2 21.0 20.4 0.6
4 24.4 21.0 20.9 0.1
5 26.0 22.1 21.3 0.8
6 28.3 22.1 21.9 0.2
7 29.6 22.4 22.2 0.2
8 32.4 22.6 22.9 -0.3
9 33.7 23.0 23.2 -0.2
10 35.7 24.3 23.7 0.6
11 38.3 23.9 24.4 -0.5
12 40.2 24.7 24.9 -0.2
新课学习
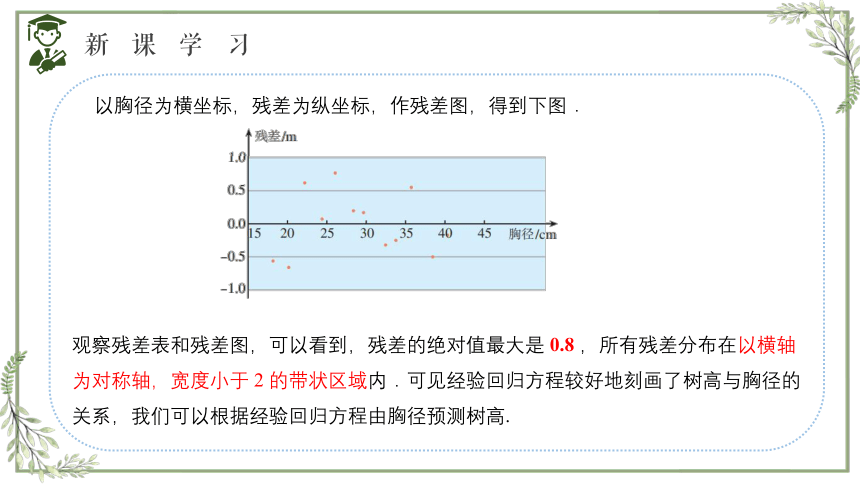
以胸径为横坐标,残差为纵坐标,作残差图,得到下图.
观察残差表和残差图,可以看到,残差的绝对值最大是 0.8 ,所有残差分布在以横轴为对称轴,宽度小于 2 的带状区域内.可见经验回归方程较好地刻画了树高与胸径的关系,我们可以根据经验回归方程由胸径预测树高.
新课学习
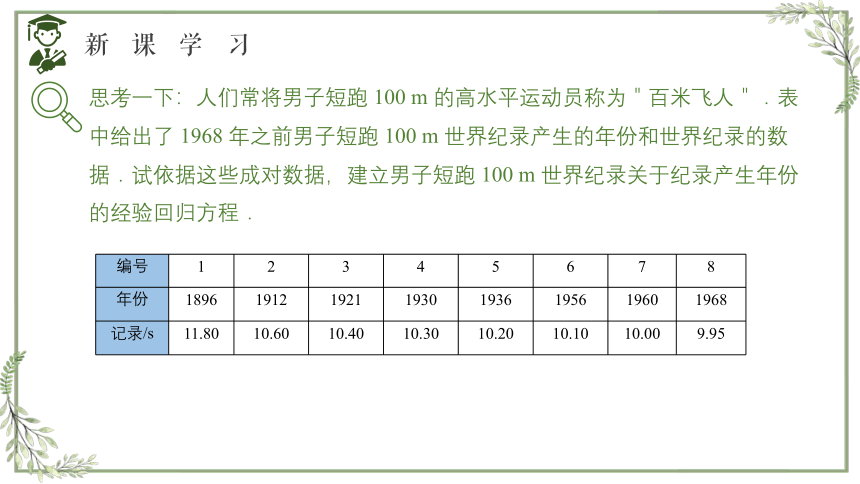
思考一下:人们常将男子短跑 100 m 的高水平运动员称为"百米飞人".表中给出了 1968 年之前男子短跑 100 m 世界纪录产生的年份和世界纪录的数据.试依据这些成对数据,建立男子短跑 100 m 世界纪录关于纪录产生年份的经验回归方程.
编号 1 2 3 4 5 6 7 8
年份 1896 1912 1921 1930 1936 1956 1960 1968
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
新课学习
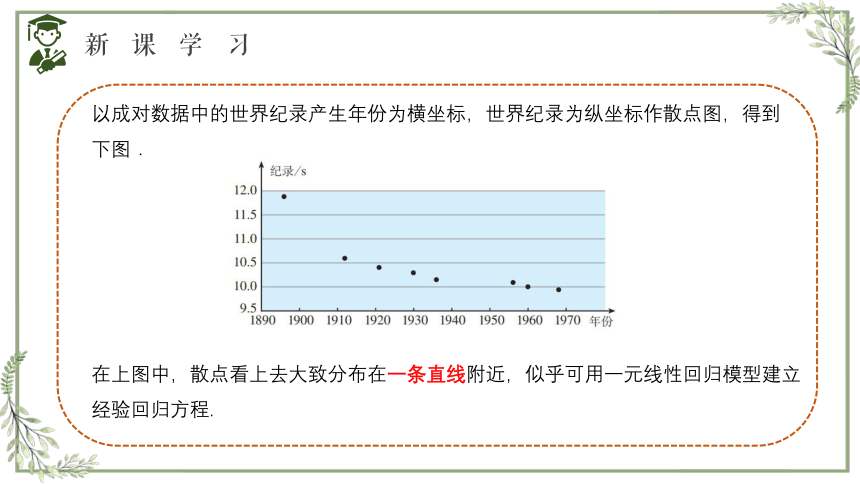
以成对数据中的世界纪录产生年份为横坐标,世界纪录为纵坐标作散点图,得到下图.
在上图中,散点看上去大致分布在一条直线附近,似乎可用一元线性回归模型建立经验回归方程.
新课学习
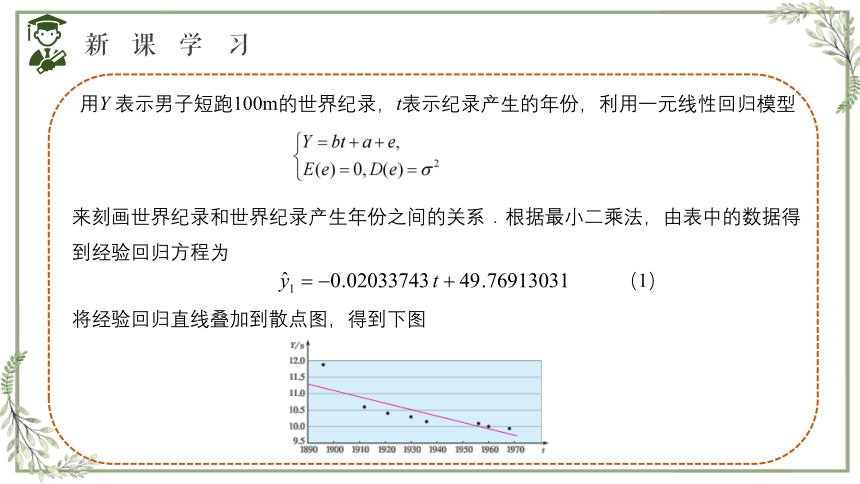
用Y 表示男子短跑100m的世界纪录,t表示纪录产生的年份,利用一元线性回归模型
来刻画世界纪录和世界纪录产生年份之间的关系.根据最小二乘法,由表中的数据得到经验回归方程为
将经验回归直线叠加到散点图,得到下图
(1)
新课学习
探究思考:从上图中可以看到,经验回归方程(1)较好地刻画了散点的变化趋势.请再仔细观察图形,你能看出其中存在的问题吗?
以经验回归直线为参照,可以发现经验回归方程的不足之处,以及散点的更为精细的分布特征.
例如,第一个世界纪录所对应的散点远离经验回归直线,并且前后两时间段中的散点都在经验回归直线的上方,中间时间段的散点都在经验回归直线的下方.这说明散点并不是随机分布在经验回归直线的周围,而是围绕着经验回归直线有一定的变化规律,即成对样本数据呈现出明显的非线性相关的特征.
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
仔细观察下图,可以发现散点更趋向于落在中间下凸且递减的某条曲线附近.
可以发现函数 y=-lnx的图象具有类似的形状特征.注意到 100m短跑的第一个世界纪录产生于1896年,因此可以认为散点是集中在曲线
y=f(t)=c1+c2 ln(t-1895)
的周围,其中c1和c2 为未知的参数,且c2 <0 .
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
用上述函数刻画数据变化的趋势,这是一个非线性经验回归函数,其中c1,c2 是待定参数.现在问题转化为如何利用成对数据估计参数c1 和c2.
为了利用一元线性回归模型估计参数c1和c2 ,我们引进一个中间变量x ,令 x= ln(t-1895)
通过 x=ln(t-1895) ,将年份变量数据进行变换,得到新的成对数据(精确到0.01),如下表所示.
编号 1 2 3 4 5 6 7 8
x 0.00 2.83 3.26 3.56 3.71 4.11 4.17 4.29
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
如果上表对应的散点图呈现出很强的线性相关特征,我们就可以借助一元线性回归模型和新的成对数据,对参数c1和c2作出估计,进而可以得到Y关于t的非线性经验回归方程.
得到散点图,如下图所示,散点的分布呈现出很强的线性相关特征.
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
因此,用一元线性回归模型
得到经验回归方程
2=-0.4264398x+11.8012653
再在上图中画出(*)式所对应的经验回归直线,得到下图.
(*)
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
由上图表明,经验回归方程(*)对于上表中的成对数据具有非常好的拟合精度.将上图与下图进行对比,可以发现 x 和 Y之间的线性相关程度比原始样本数据的线性相关程度强得多.
将 x=ln(t-1895) 代人(*)式,得到由创纪录年份预报世界纪录的经验回归方程
2=-0.4264398ln(t-1895)+11.8012653
在同一直角坐标系中画出成对数据散点图,非线性经验回归方程(2)的图象以及经验回归方程(1)的图象,如下图所示.
(2)
新课学习
我们发现,散点图中各散点都非常靠近(2)的图象,表明非线性经验回归方程(2)对于原始数据的拟合效果远远好于经验回归方程(1).
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
下面通过残差来比较这两个经验回归方程对数据刻画的好坏.在表中,用ti表示编号为i的年份数据,用yi 表示编号为i的纪录数据,则经验回归方程(1)和(2)的残差计算公式分别为
2=yi+0.02033743ti-49.76913031,i=1,2, ,8;
2=yi+0.4264398ln(ti-1895)-11.8012653,i=1,2, ,8.
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
①
②
散点图中各散点都非常靠近②的图象, 表明非线性经验回归方程②对于原始数据的拟合效果远远好于经验回归方程①.
编号 1 2 3 4 5 6 7 8
t 1896 1912 1921 1930 1936 1956 1960 1960
0.591 -0.284 -0.301 -0.218 -0.196 0.111 0.092 0.205
-0.001 0.007 -0.012 0.015 -0.018 0.052 -0.021 -0.022
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
在一般情况下,直接比较两个模型的残差比较困难,因为在某些散点上一个模型的残差的绝对值比另一个模型的小,而另一些散点的情况则相反.可以通过比较残差的平方和来比较两个模型的效果.由
可知Q2 小于 Q1 .
的拟合效果要优于一元线性回归模型的拟合效果.
因此在残差平方和最小的标准下,非线性回归模型
新课学习
用R2比较模型的拟合效果
也可以用决定系数 R2 来比较两个模型的拟合效果,R2的计算公式为
新课学习
思考一下:根据上面的公式计算一下回归方程(1)和回归方程(2),哪个拟合效果更好?
由上表容易算出经验回归方程(1)和(2)的 R2 分别约为 0.7325 和 0.9983 ,因此经验回归方程(2)的刻画效果比经验回归方程(1)的好很多.
另外,我们还可以用新的观测数据来检验模型的拟合效果.事实上,我们还有1968年之后的男子短跑100 m世界纪录数据,如下表所示.
编号 9 10 11 12 13 14 15 16 17 18 19 20 21
t 1983 1988 1991 1991 1994 1996 1999 2002 2005 2007 2008 2008 2009
Y/s 9.93 9.92 9.90 9.86 9.85 9.84 9.79 9.78 9.77 9.74 9.72 9.69 9.58
新课学习
在下面的散点图中,绘制上表中的散点(绿色),再添加经验回归方程(1)所对应的经验回归直线(红色),以及经验回归方程(2)所对应的经验回归曲线(蓝色),得到下图 .显然绿色散点分布在蓝色经验回归曲线的附近,远离红色经验回归直线,表明经验回归方程(2)对于新数据的预报效果远远好于(1).
新课学习
在使用经验回归方程进行预测时,需要注意下列问题
(1)经验回归方程只适用于所研究的样本的总体.例如,根据我国父亲身高与儿子身高的数据建立的经验回归方程,不能用来描述美国父亲身高与儿子身高之间的关系.同样,根据生长在南方多雨地区的树高与胸径的数据建立的经验回归方程,不能用来描述北方干旱地区的树高与胸径之间的关系.
(2)经验回归方程一般都有时效性.例如,根据 20 世纪 80 年代的父亲身高与儿子身高的数据建立的经验回归方程,不能用来描述现在的父亲身高与儿子身高之间的关系.
新课学习
在使用经验回归方程进行预测时,需要注意下列问题
(3)解释变量的取值不能离样本数据的范围太远.一般解释变量的取值在样本数据范围内,经验回归方程的预报效果会比较好,超出这个范围越远,预报的效果越差.
(4)不能期望经验回归方程得到的预报值就是响应变量的精确值.事实上,它是响应变量的可能取值的平均值.
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
0.5
课堂巩固
总结一下
2.用R2比较模型的拟合效果
3.在使用经验回归方程进行预测时,需要注意的问题
1.非线性回归分析
感谢同学们观看
8.2 一元线性回归模型及其应用
(第二课时)
人教A版(2019)选择性必修三
素养目标
1.针对实际问题,会用一元线性回归模型进行预测,提升逻辑推理能力(重点)
2.通过对具体问题的进一步分析,能将某些非线性回归问题转化为线性回归问题并加以解决,提升数学运算能力(重点)
3.通过具体实例,了解决定系数R2的意义和作用,提升逻辑推理能力(难点)
新课导入
思考一下:观察图中四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定?
(1)
(2)
(3)
(4)
新课学习
根据一元线性回归模型中对随机误差的假定,残差应是均值为0 ,方差为σ2 的随机变量的观测值.
图(1)显示残差与观测时间有线性关系,应将时间变量纳入模型;
图(2)显示残差与观测时间有非线性关系,应在模型中加入时间的非线性函数部分;
图(3)说明残差的方差不是一个常数,随观测时间变大而变大;
图(4)的残差比较均匀地分布在以取值为0的横轴为对称轴的水平带状区域内.
可见,在图中,只有图(4)满足一元线性回归模型对随机误差的假设.
新课学习
例 经验表明,一般树的胸径(树的主干在地面以上1.3m处的直径)越大,树就越高.由于测量树高比测量胸径困难,因此研究人员希望由胸径预测树高.在研究树高与胸径之间的关系时,某林场收集了某种树的一些数据(如下表),试根据这些数据建立树高关于胸径的经验回归方程.
编号 1 2 3 4 5 6
胸径/cm 18.1 20.1 22.2 24.4 26.0 28.3
树高/m 18.8 19.2 21.0 21.0 22.1 22.1
编号 7 8 9 10 11 12
胸径/cm 29.6 32.4 33.7 35.7 38.3 40.2
树高/m 22.4 22.6 23.0 24.3 23.9 24.7
新课学习
分析:因为要由胸径预测树高,所以要以成对样本数据的胸径为横坐标,树高为纵坐标画出散点,进而得到散点图,再根据散点图推断树高与胸径是否线性相关.如果是,再利用公式计算出 ,即可.
以胸径为横坐标,树高为纵坐标作散点图,得到下图 .
新课学习
在上图中,散点大致分布在一条从左下角到右上角的直线附近,表明两个变量线性相关,并且是正相关,因此可以用一元线性回归模型刻画树高与胸径之间的关系.
用d表示胸径,h表示树高,根据最小二乘法,计算可得经验回归方程为
相应的经验回归直线如图所示.
新课学习
根据经验回归方程,由例题中所给表中胸径的数据可以计算出树高的预测值(精确到0.1)以及相应的残差,如下表所示.
编号 胸径/cm 树高观测值/m 树高预测值/m 残差/m
1 18.1 18.8 19.4 -0.6
2 20.1 19.2 19.9 -0.7
3 22.2 21.0 20.4 0.6
4 24.4 21.0 20.9 0.1
5 26.0 22.1 21.3 0.8
6 28.3 22.1 21.9 0.2
7 29.6 22.4 22.2 0.2
8 32.4 22.6 22.9 -0.3
9 33.7 23.0 23.2 -0.2
10 35.7 24.3 23.7 0.6
11 38.3 23.9 24.4 -0.5
12 40.2 24.7 24.9 -0.2
新课学习
以胸径为横坐标,残差为纵坐标,作残差图,得到下图.
观察残差表和残差图,可以看到,残差的绝对值最大是 0.8 ,所有残差分布在以横轴为对称轴,宽度小于 2 的带状区域内.可见经验回归方程较好地刻画了树高与胸径的关系,我们可以根据经验回归方程由胸径预测树高.
新课学习
思考一下:人们常将男子短跑 100 m 的高水平运动员称为"百米飞人".表中给出了 1968 年之前男子短跑 100 m 世界纪录产生的年份和世界纪录的数据.试依据这些成对数据,建立男子短跑 100 m 世界纪录关于纪录产生年份的经验回归方程.
编号 1 2 3 4 5 6 7 8
年份 1896 1912 1921 1930 1936 1956 1960 1968
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
新课学习
以成对数据中的世界纪录产生年份为横坐标,世界纪录为纵坐标作散点图,得到下图.
在上图中,散点看上去大致分布在一条直线附近,似乎可用一元线性回归模型建立经验回归方程.
新课学习
用Y 表示男子短跑100m的世界纪录,t表示纪录产生的年份,利用一元线性回归模型
来刻画世界纪录和世界纪录产生年份之间的关系.根据最小二乘法,由表中的数据得到经验回归方程为
将经验回归直线叠加到散点图,得到下图
(1)
新课学习
探究思考:从上图中可以看到,经验回归方程(1)较好地刻画了散点的变化趋势.请再仔细观察图形,你能看出其中存在的问题吗?
以经验回归直线为参照,可以发现经验回归方程的不足之处,以及散点的更为精细的分布特征.
例如,第一个世界纪录所对应的散点远离经验回归直线,并且前后两时间段中的散点都在经验回归直线的上方,中间时间段的散点都在经验回归直线的下方.这说明散点并不是随机分布在经验回归直线的周围,而是围绕着经验回归直线有一定的变化规律,即成对样本数据呈现出明显的非线性相关的特征.
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
仔细观察下图,可以发现散点更趋向于落在中间下凸且递减的某条曲线附近.
可以发现函数 y=-lnx的图象具有类似的形状特征.注意到 100m短跑的第一个世界纪录产生于1896年,因此可以认为散点是集中在曲线
y=f(t)=c1+c2 ln(t-1895)
的周围,其中c1和c2 为未知的参数,且c2 <0 .
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
用上述函数刻画数据变化的趋势,这是一个非线性经验回归函数,其中c1,c2 是待定参数.现在问题转化为如何利用成对数据估计参数c1 和c2.
为了利用一元线性回归模型估计参数c1和c2 ,我们引进一个中间变量x ,令 x= ln(t-1895)
通过 x=ln(t-1895) ,将年份变量数据进行变换,得到新的成对数据(精确到0.01),如下表所示.
编号 1 2 3 4 5 6 7 8
x 0.00 2.83 3.26 3.56 3.71 4.11 4.17 4.29
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
如果上表对应的散点图呈现出很强的线性相关特征,我们就可以借助一元线性回归模型和新的成对数据,对参数c1和c2作出估计,进而可以得到Y关于t的非线性经验回归方程.
得到散点图,如下图所示,散点的分布呈现出很强的线性相关特征.
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
因此,用一元线性回归模型
得到经验回归方程
2=-0.4264398x+11.8012653
再在上图中画出(*)式所对应的经验回归直线,得到下图.
(*)
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
由上图表明,经验回归方程(*)对于上表中的成对数据具有非常好的拟合精度.将上图与下图进行对比,可以发现 x 和 Y之间的线性相关程度比原始样本数据的线性相关程度强得多.
将 x=ln(t-1895) 代人(*)式,得到由创纪录年份预报世界纪录的经验回归方程
2=-0.4264398ln(t-1895)+11.8012653
在同一直角坐标系中画出成对数据散点图,非线性经验回归方程(2)的图象以及经验回归方程(1)的图象,如下图所示.
(2)
新课学习
我们发现,散点图中各散点都非常靠近(2)的图象,表明非线性经验回归方程(2)对于原始数据的拟合效果远远好于经验回归方程(1).
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
下面通过残差来比较这两个经验回归方程对数据刻画的好坏.在表中,用ti表示编号为i的年份数据,用yi 表示编号为i的纪录数据,则经验回归方程(1)和(2)的残差计算公式分别为
2=yi+0.02033743ti-49.76913031,i=1,2, ,8;
2=yi+0.4264398ln(ti-1895)-11.8012653,i=1,2, ,8.
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
①
②
散点图中各散点都非常靠近②的图象, 表明非线性经验回归方程②对于原始数据的拟合效果远远好于经验回归方程①.
编号 1 2 3 4 5 6 7 8
t 1896 1912 1921 1930 1936 1956 1960 1960
0.591 -0.284 -0.301 -0.218 -0.196 0.111 0.092 0.205
-0.001 0.007 -0.012 0.015 -0.018 0.052 -0.021 -0.022
新课学习
思考一下:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
在一般情况下,直接比较两个模型的残差比较困难,因为在某些散点上一个模型的残差的绝对值比另一个模型的小,而另一些散点的情况则相反.可以通过比较残差的平方和来比较两个模型的效果.由
可知Q2 小于 Q1 .
的拟合效果要优于一元线性回归模型的拟合效果.
因此在残差平方和最小的标准下,非线性回归模型
新课学习
用R2比较模型的拟合效果
也可以用决定系数 R2 来比较两个模型的拟合效果,R2的计算公式为
新课学习
思考一下:根据上面的公式计算一下回归方程(1)和回归方程(2),哪个拟合效果更好?
由上表容易算出经验回归方程(1)和(2)的 R2 分别约为 0.7325 和 0.9983 ,因此经验回归方程(2)的刻画效果比经验回归方程(1)的好很多.
另外,我们还可以用新的观测数据来检验模型的拟合效果.事实上,我们还有1968年之后的男子短跑100 m世界纪录数据,如下表所示.
编号 9 10 11 12 13 14 15 16 17 18 19 20 21
t 1983 1988 1991 1991 1994 1996 1999 2002 2005 2007 2008 2008 2009
Y/s 9.93 9.92 9.90 9.86 9.85 9.84 9.79 9.78 9.77 9.74 9.72 9.69 9.58
新课学习
在下面的散点图中,绘制上表中的散点(绿色),再添加经验回归方程(1)所对应的经验回归直线(红色),以及经验回归方程(2)所对应的经验回归曲线(蓝色),得到下图 .显然绿色散点分布在蓝色经验回归曲线的附近,远离红色经验回归直线,表明经验回归方程(2)对于新数据的预报效果远远好于(1).
新课学习
在使用经验回归方程进行预测时,需要注意下列问题
(1)经验回归方程只适用于所研究的样本的总体.例如,根据我国父亲身高与儿子身高的数据建立的经验回归方程,不能用来描述美国父亲身高与儿子身高之间的关系.同样,根据生长在南方多雨地区的树高与胸径的数据建立的经验回归方程,不能用来描述北方干旱地区的树高与胸径之间的关系.
(2)经验回归方程一般都有时效性.例如,根据 20 世纪 80 年代的父亲身高与儿子身高的数据建立的经验回归方程,不能用来描述现在的父亲身高与儿子身高之间的关系.
新课学习
在使用经验回归方程进行预测时,需要注意下列问题
(3)解释变量的取值不能离样本数据的范围太远.一般解释变量的取值在样本数据范围内,经验回归方程的预报效果会比较好,超出这个范围越远,预报的效果越差.
(4)不能期望经验回归方程得到的预报值就是响应变量的精确值.事实上,它是响应变量的可能取值的平均值.
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
0.5
课堂巩固
总结一下
2.用R2比较模型的拟合效果
3.在使用经验回归方程进行预测时,需要注意的问题
1.非线性回归分析
感谢同学们观看
