8.3.1 分类变量与列联表 教学课件(共30张PPT)高中数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 8.3.1 分类变量与列联表 教学课件(共30张PPT)高中数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 46.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 12:58:42 | ||
图片预览










文档简介
(共30张PPT)
8.3.1 分类变量与列联表
人教A版(2019)选择性必修三
素养目标
1.通过对典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法,提升逻辑推理素养(重点)
2.了解独立性检验(只要求2×2列联表)的应用,提升数学运算能力(难点)
新课导入
1.就读不同学校是否对学生的成绩有影响?
2.不同班级学生用于体育锻炼的时间是否有差别?
3.吸烟是否会增加患肺癌的风险?
思考一下:思考下面的几个问题:
这些问题都是一定范围内的两种现象或性质之间是否存在关联性或相互影响的问题.
本节将要学习的独立性检验方法为我们提供了解决这类问题的方案.
新课学习
分类变量的概念
为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量.
分类变量的取值可以用实数表示,例如,学生所在的班级可以用 1,2,3 等表示,男性,女性可以用 1,0 表示,等等.在很多时候,这些数值只作为编号使用,
新课学习
思考一下:思考下面的问题:
为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查,全校学生的普查数据如下:523名女生中有331名经常锻炼;601名男生中有473名经常锻炼.你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗
新课学习
解法一:我们设
那么,只要求出 f0 和 f1 的值,通过比较这两个值的大小,就可以知道女生和男生在锻炼的经常性方面是否有差异.由所给的数据,经计算得到
由 f1-f0≈0.787-0.633=0.154
可知,男生经常锻炼的比率比女生高出15.4 个百分点,所以该校的女生和男生在体育锻炼的经常性方面有差异,而且男生更经常锻炼.
新课学习
解法二:用 Ω 表示该校全体学生构成的集合,这是我们所关心的对象的总体.考虑以 Ω 为样本空间的古典概型,并定义一对分类变量 X 和Y如下:对于 Ω 中的每一名学生,分别令
如果从该校女生和男生中各随机选取一名学生,那么该女生属于经常锻炼群体的概率是 P(Y=1∣X=0) ,而该男生属于经常锻炼群体的概率是P(Y=1∣X=1) .
因此,“性别对体育锻炼的经常性没有影响”可以描述为
P(Y=1∣X=0)=P(Y=1∣X=1);
新课学习
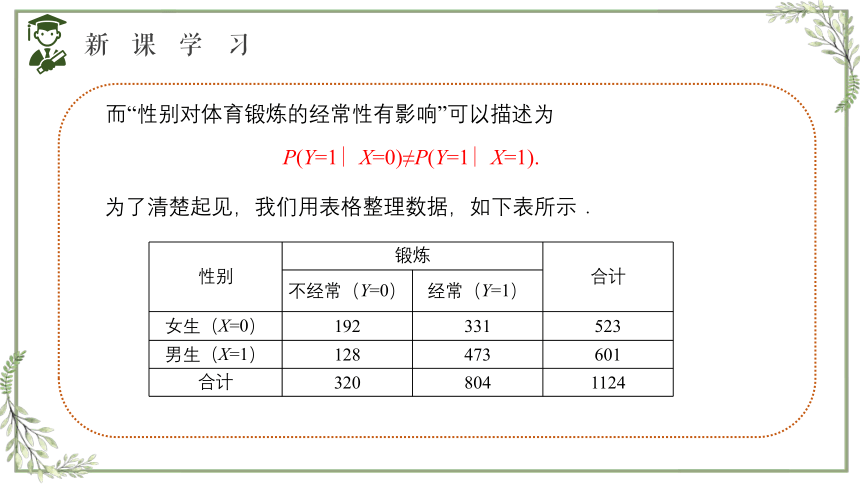
而“性别对体育锻炼的经常性有影响”可以描述为
P(Y=1∣X=0)≠P(Y=1∣X=1).
为了清楚起见,我们用表格整理数据,如下表所示.
性别 锻炼 合计
不经常(Y=0) 经常(Y=1) 女生(X=0) 192 331 523
男生(X=1) 128 473 601
合计 320 804 1124
新课学习
我们用 {X=0,Y=1} 表示事件 {X=0} 和 {Y=1} 的积事件,用 {X=1,Y=1} 表示事件 {X=1} 和 {Y=1} 的积事件.根据古典概型和条件概率的计算公式,我们有
由 P(Y=1∣X=1) 大于 P(Y=1∣X=0) 可以作出判断,在该校的学生中,性别对体育锻炼的经常性有影响,即该校的女生和男生在体育锻炼的经常性方面存在差异,而且男生更经常锻炼.
新课学习
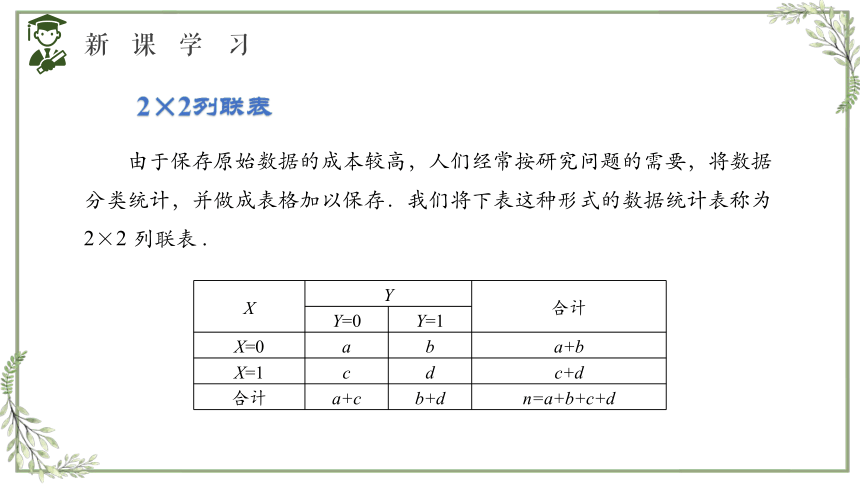
2×2列联表
由于保存原始数据的成本较高,人们经常按研究问题的需要,将数据分类统计,并做成表格加以保存.我们将下表这种形式的数据统计表称为 2×2 列联表 .
X Y 合计
Y=0 Y=1 X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
新课学习
2×2列联表表示的意义
2×2 列联表给出了成对分类变量数据的交叉分类频数.
以上表为例,它包含了X 和Y的如下信息:最后一行的前两个数分别是事件{Y=0}和{Y=1} 中样本点的个数;最后一列的前两个数分别是事件{X=0} 和 {X=1} 中样本点的个数;中间的四个格中的数是表格的核心部分,给出了事件{X=x,Y=y}
(x,y=0,1) 中样本点的个数;右下角格中的数是样本空间中样本点的总数.
新课学习
统计案例常用方法
对于大多数实际问题,我们无法获得所关心的全部对象的数据,因此无法准确计算出有关的比率或条件概率.在这种情况下,上述古典概型和条件概率的观点为我们提供了一个解决问题的思路.比较简单的做法是利用随机抽样获得一定数量的样本数据,再利用随机事件发生的频率稳定于概率的原理对问题答案作出推断.
新课学习
例 1 为比较甲,乙两所学校学生的数学水平,采用简单随机抽样的方法抽取 88 名学生.通过测验得到了如下数据:甲校 43 名学生中有 10 名数学成绩优秀;乙校 45 名学生中有 7 名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
用 Ω 表示两所学校的全体学生构成的集合.考虑以 Ω 为样本空间的古典概型.对于 Ω 中每一名学生,定义分类变量 X 和 Y 如下:
我们将所给数据整理成下表
新课学习
学校 数学成绩 合计
不优秀(Y=0) 优秀(Y=1) 甲校(X=0) 33 10 43
乙校(X=1) 38 7 45
合计 71 17 88
表中的数据是关于分类变量 X 和Y的抽样数据的2×2 列联表:最后一行的前两个数分别是事件{Y=0}和{Y=1}的频数;最后一列的前两个数分别是事件{X=0} 和{X=1}的频数;中间的四个格中的数是事件 {X=x,Y=y}(x,y=0,1) 的频数;右下角格中的数是样本容量.
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为
新课学习
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为
我们可以用等高堆积条形图直观地展示上述计算结果,如图所示.
左边的蓝色和红色条的高度分别是甲校学生中数学成绩不优秀和数学成绩优秀的频率;
右边的蓝色和红色条的高度分别是乙校学生中数学成绩不优秀和数学成绩优秀的频率.
新课学习
通过比较发现的频率明显高于乙校的频率.依据频率稳定于概率的原理,我们可以推断P(Y=1∣X=0)>P(Y=1∣X=1) .
通过比较发现,两个学校学生抽样数据中数学成绩优秀的频率存在差异,甲校的频率明显高于乙校的频率.
依据频率稳定于概率的原理,我们可以推断 P(Y=1∣X=0)>P(Y=1∣X=1) .
也就是说,如果从甲校和乙校各随机选取一名学生,那么甲校学生数学成绩优秀的概率大于乙校学生数学成绩优秀的概率.因此,可以认为两校学生的数学成绩优秀率存在差异,甲校学生的数学成绩优秀率比乙校学生的高.
新课学习
思考一下:你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
事实上,"两校学生的数学成绩优秀率存在差异"这个结论是根据两个频率间存在差异推断出来的.有可能出现这种情况:在随机抽取的这个样本中,两个频率间确实存在差异,但两校学生的数学成绩优秀率实际上是没有差别的.
这就是说,样本的随机性导致了两个频率间出现较大差异.在这种情况下,我们推断出的结论就是错误的.
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
D
课堂巩固
课堂巩固
是
课堂巩固
课堂总结
1.分类变量的概念
2.2×2列联表
3.统计案例常用方法
感谢同学们观看
8.3.1 分类变量与列联表
人教A版(2019)选择性必修三
素养目标
1.通过对典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法,提升逻辑推理素养(重点)
2.了解独立性检验(只要求2×2列联表)的应用,提升数学运算能力(难点)
新课导入
1.就读不同学校是否对学生的成绩有影响?
2.不同班级学生用于体育锻炼的时间是否有差别?
3.吸烟是否会增加患肺癌的风险?
思考一下:思考下面的几个问题:
这些问题都是一定范围内的两种现象或性质之间是否存在关联性或相互影响的问题.
本节将要学习的独立性检验方法为我们提供了解决这类问题的方案.
新课学习
分类变量的概念
为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量.
分类变量的取值可以用实数表示,例如,学生所在的班级可以用 1,2,3 等表示,男性,女性可以用 1,0 表示,等等.在很多时候,这些数值只作为编号使用,
新课学习
思考一下:思考下面的问题:
为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查,全校学生的普查数据如下:523名女生中有331名经常锻炼;601名男生中有473名经常锻炼.你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗
新课学习
解法一:我们设
那么,只要求出 f0 和 f1 的值,通过比较这两个值的大小,就可以知道女生和男生在锻炼的经常性方面是否有差异.由所给的数据,经计算得到
由 f1-f0≈0.787-0.633=0.154
可知,男生经常锻炼的比率比女生高出15.4 个百分点,所以该校的女生和男生在体育锻炼的经常性方面有差异,而且男生更经常锻炼.
新课学习
解法二:用 Ω 表示该校全体学生构成的集合,这是我们所关心的对象的总体.考虑以 Ω 为样本空间的古典概型,并定义一对分类变量 X 和Y如下:对于 Ω 中的每一名学生,分别令
如果从该校女生和男生中各随机选取一名学生,那么该女生属于经常锻炼群体的概率是 P(Y=1∣X=0) ,而该男生属于经常锻炼群体的概率是P(Y=1∣X=1) .
因此,“性别对体育锻炼的经常性没有影响”可以描述为
P(Y=1∣X=0)=P(Y=1∣X=1);
新课学习
而“性别对体育锻炼的经常性有影响”可以描述为
P(Y=1∣X=0)≠P(Y=1∣X=1).
为了清楚起见,我们用表格整理数据,如下表所示.
性别 锻炼 合计
不经常(Y=0) 经常(Y=1) 女生(X=0) 192 331 523
男生(X=1) 128 473 601
合计 320 804 1124
新课学习
我们用 {X=0,Y=1} 表示事件 {X=0} 和 {Y=1} 的积事件,用 {X=1,Y=1} 表示事件 {X=1} 和 {Y=1} 的积事件.根据古典概型和条件概率的计算公式,我们有
由 P(Y=1∣X=1) 大于 P(Y=1∣X=0) 可以作出判断,在该校的学生中,性别对体育锻炼的经常性有影响,即该校的女生和男生在体育锻炼的经常性方面存在差异,而且男生更经常锻炼.
新课学习
2×2列联表
由于保存原始数据的成本较高,人们经常按研究问题的需要,将数据分类统计,并做成表格加以保存.我们将下表这种形式的数据统计表称为 2×2 列联表 .
X Y 合计
Y=0 Y=1 X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
新课学习
2×2列联表表示的意义
2×2 列联表给出了成对分类变量数据的交叉分类频数.
以上表为例,它包含了X 和Y的如下信息:最后一行的前两个数分别是事件{Y=0}和{Y=1} 中样本点的个数;最后一列的前两个数分别是事件{X=0} 和 {X=1} 中样本点的个数;中间的四个格中的数是表格的核心部分,给出了事件{X=x,Y=y}
(x,y=0,1) 中样本点的个数;右下角格中的数是样本空间中样本点的总数.
新课学习
统计案例常用方法
对于大多数实际问题,我们无法获得所关心的全部对象的数据,因此无法准确计算出有关的比率或条件概率.在这种情况下,上述古典概型和条件概率的观点为我们提供了一个解决问题的思路.比较简单的做法是利用随机抽样获得一定数量的样本数据,再利用随机事件发生的频率稳定于概率的原理对问题答案作出推断.
新课学习
例 1 为比较甲,乙两所学校学生的数学水平,采用简单随机抽样的方法抽取 88 名学生.通过测验得到了如下数据:甲校 43 名学生中有 10 名数学成绩优秀;乙校 45 名学生中有 7 名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
用 Ω 表示两所学校的全体学生构成的集合.考虑以 Ω 为样本空间的古典概型.对于 Ω 中每一名学生,定义分类变量 X 和 Y 如下:
我们将所给数据整理成下表
新课学习
学校 数学成绩 合计
不优秀(Y=0) 优秀(Y=1) 甲校(X=0) 33 10 43
乙校(X=1) 38 7 45
合计 71 17 88
表中的数据是关于分类变量 X 和Y的抽样数据的2×2 列联表:最后一行的前两个数分别是事件{Y=0}和{Y=1}的频数;最后一列的前两个数分别是事件{X=0} 和{X=1}的频数;中间的四个格中的数是事件 {X=x,Y=y}(x,y=0,1) 的频数;右下角格中的数是样本容量.
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为
新课学习
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为
我们可以用等高堆积条形图直观地展示上述计算结果,如图所示.
左边的蓝色和红色条的高度分别是甲校学生中数学成绩不优秀和数学成绩优秀的频率;
右边的蓝色和红色条的高度分别是乙校学生中数学成绩不优秀和数学成绩优秀的频率.
新课学习
通过比较发现的频率明显高于乙校的频率.依据频率稳定于概率的原理,我们可以推断P(Y=1∣X=0)>P(Y=1∣X=1) .
通过比较发现,两个学校学生抽样数据中数学成绩优秀的频率存在差异,甲校的频率明显高于乙校的频率.
依据频率稳定于概率的原理,我们可以推断 P(Y=1∣X=0)>P(Y=1∣X=1) .
也就是说,如果从甲校和乙校各随机选取一名学生,那么甲校学生数学成绩优秀的概率大于乙校学生数学成绩优秀的概率.因此,可以认为两校学生的数学成绩优秀率存在差异,甲校学生的数学成绩优秀率比乙校学生的高.
新课学习
思考一下:你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
事实上,"两校学生的数学成绩优秀率存在差异"这个结论是根据两个频率间存在差异推断出来的.有可能出现这种情况:在随机抽取的这个样本中,两个频率间确实存在差异,但两校学生的数学成绩优秀率实际上是没有差别的.
这就是说,样本的随机性导致了两个频率间出现较大差异.在这种情况下,我们推断出的结论就是错误的.
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
D
课堂巩固
课堂巩固
是
课堂巩固
课堂总结
1.分类变量的概念
2.2×2列联表
3.统计案例常用方法
感谢同学们观看
