【备考2025】中考数学真题2022-2024分类精编精练6坐标系与一次函数(含解析)
文档属性
| 名称 | 【备考2025】中考数学真题2022-2024分类精编精练6坐标系与一次函数(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-04 22:01:35 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【备考2025】中考数学真题2022-2024分类精编精练6坐标系与一次函数
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.(2023·浙江·)在平面直角坐标系中,点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2022·浙江温州·)小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图像,能近似刻画s与t之间关系的是( )
A. B.
C. D.
3.(2023·浙江·)一个球从地面竖直向上弹起时的速度为10米/秒,经过(秒)时球距离地面的高度(米)适用公式,那么球弹起后又回到地面所花的时间(秒)是( )
A.5 B.10 C.1 D.2
4.(2023·浙江嘉兴·)下图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )
A. B.
C. D.
5.(2023·浙江台州·)如图是中国象棋棋盘的一部分,建立如图所示的平面直角坐标系,已知“车”所在位置的坐标为,则“炮”所在位置的坐标为( ).
A. B. C. D.
6.(2022·浙江绍兴·)已知为直线上的三个点,且,则以下判断正确的是( ).
A.若,则 B.若,则
C.若,则 D.若,则
7.(2022·浙江金华·)如图是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是,下列各地点中,离原点最近的是( )
A.超市 B.医院 C.体育场 D.学校
8.(2022·浙江舟山·)已知点,在直线(k为常数,)上,若的最大值为9,则c的值为( )
A. B.2 C. D.1
9.(2022·浙江衢州·)西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端(人眼)望点,使视线通过点,记人站立的位置为点,量出长,即可算得物高.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则关于的函数表达式为( )
A. B. C. D.
10.(2023·浙江温州·)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.
【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟.小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.
【问题】路线①③⑥⑦⑧各路段路程之和为( )
A.4200米 B.4800米 C.5200米 D.5400米
二、填空题
11.(2022·浙江杭州·)已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组的解是 .
12.(2023·浙江衢州·)在如图所示的方格纸上建立适当的平面直角坐标系,若点A的坐标为,点B的坐标为,则点C的坐标为 .
13.(2022·浙江丽水·)三个能够重合的正六边形的位置如图.已知B点的坐标是,则A点的坐标是 .
14.(2023·浙江杭州·)在“ “探索一次函数的系数与图像的关系”活动中,老师给出了直角坐标系中的三个点:.同学们画出了经过这三个点中每两个点的一次函数的图像,并得到对应的函数表达式.分别计算,的值,其中最大的值等于 .
三、解答题
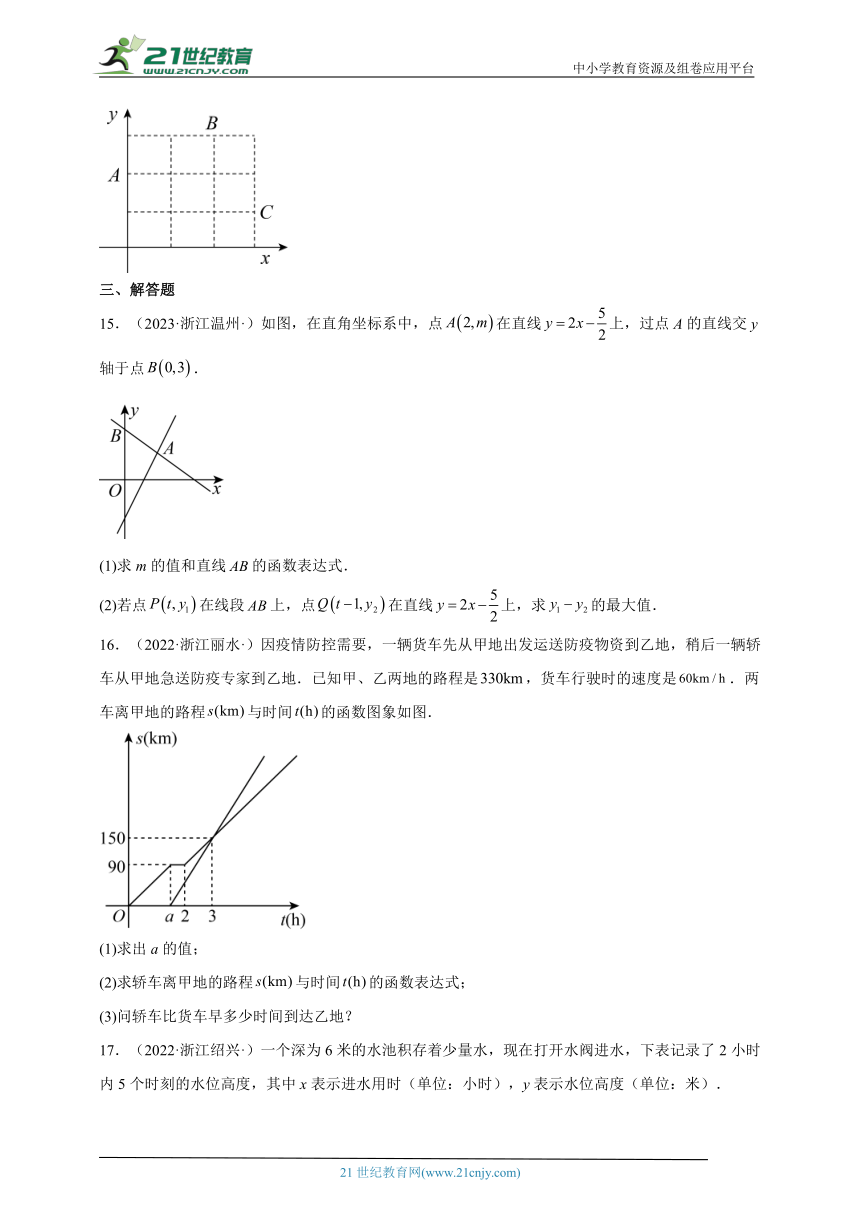
15.(2023·浙江温州·)如图,在直角坐标系中,点在直线上,过点A的直线交y轴于点.
(1)求m的值和直线的函数表达式.
(2)若点在线段上,点在直线上,求的最大值.
16.(2022·浙江丽水·)因疫情防控需要,一辆货车先从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地.已知甲、乙两地的路程是,货车行驶时的速度是.两车离甲地的路程与时间的函数图象如图.
(1)求出a的值;
(2)求轿车离甲地的路程与时间的函数表达式;
(3)问轿车比货车早多少时间到达乙地?
17.(2022·浙江绍兴·)一个深为6米的水池积存着少量水,现在打开水阀进水,下表记录了2小时内5个时刻的水位高度,其中x表示进水用时(单位:小时),y表示水位高度(单位:米).
x 0 0.5 1 1.5 2
y 1 1.5 2 2.5 3
为了描述水池水位高度与进水用时的关系,现有以下三种函数模型供选择:(),y=ax2+bx+c (),().
(1)在平面直角坐标系中描出表中数据对应的点,再选出最符合实际的函数模型,求出相应的函数表达式,并画出这个函数的图像.
(2)当水位高度达到5米时,求进水用时x.
18.(2023·浙江绍兴·)一条笔直的路上依次有三地,其中两地相距1000米.甲、乙两机器人分别从两地同时出发,去目的地,匀速而行.图中分别表示甲、乙机器人离地的距离(米)与行走时间(分钟)的函数关系图象.
(1)求所在直线的表达式.
(2)出发后甲机器人行走多少时间,与乙机器人相遇?
(3)甲机器人到地后,再经过1分钟乙机器人也到地,求两地间的距离.
19.(2023·浙江·)我市“共富工坊”问海借力,某公司产品销售量得到大幅提升.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.看图解答下列问题:
(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2)求方案二y关于x的函数表达式;
(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.
20.(2023·浙江金华·)兄妹俩放学后沿图1中的马路从学校出发,到书吧看书后回家,哥哥步行先出发,途中速度保持不变;妺妺骑车,到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程(米)与哥哥离开学校的时间(分)的函数关系.
(1)求哥哥步行的速度.
(2)已知妺妺比哥哥迟2分钟到书吧.
①求图中的值;
②妺妺在书吧待了10分钟后回家,速度是哥哥的倍,能否在哥哥到家前追上哥哥?若能,求追上时兄妺俩离家还有多远;若不能,说明理由.
21.(2023·浙江宁波·)某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学,上午8:00,军车在离营地的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.
(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值,
(2)求部队官兵在仓库领取物资所用的时间.
22.(2024·浙江·)小明和小丽在跑步机上慢跑锻炼.小明先跑,10分钟后小丽才开始跑,小丽跑步时中间休息了两次.跑步机上C档比B档快40米/分、B档比A档快40米/分.小明与小丽的跑步相关信息如表所示,跑步累计里程s(米)与小明跑步时间t(分)的函数关系如图所示.
时间 里程分段 速度档 跑步里程
小明 不分段 A档 4000米
小丽 第一段 B档 1800米
第一次休息
第二段 B档 1200米
第二次休息
第三段 C档 1600米
(1)求A,B,C各档速度(单位:米/分);
(2)求小丽两次休息时间的总和(单位:分);
(3)小丽第二次休息后,在a分钟时两人跑步累计里程相等,求a的值.
23.(2023·浙江绍兴·)如果两点到一条直线的距离相等,则称该直线为“两点的等距线”.
(1) 如图1,直线经过线段的中点P,试说明直线是点A,B的一条等距线.
(2)如图2,是正方形网格中的三个格点,请在网格中作出所有的直线m,使直线m过点C且直线m是“两点的等距线”.
(3)如图3,中,,则在坐标轴上是否存在点P,使?若存在,试求出点P的坐标;若不存在,请说明理由.
参考答案
1.【考点】判断点所在的象限
【分析】根据点坐标分别判断出横坐标和纵坐标的符号,从而就可以判断改点所在的象限.
解:,
,,
满足第二象限的条件.
故选:B.
【点评】本题考查的是平面直角坐标系中点的坐标以及象限知识,解题的关键在于熟练掌握各个象限的横纵坐标点的符号特点.
2.【考点】函数图象识别
【分析】分别对每段时间的路程与时间的变化情况进行分析,画出路程与时间图像,再与选项对比判断即可.
解:对各段时间与路程的关系进行分析如下:
从家到凉亭,用时10分钟,路程600米,s从0增加到600米,t从0到10分,对应图像为
在凉亭休息10分钟,t从10分到20分,s保持600米不变,对应图像为
从凉亭到公园,用时间10分钟,路程600米,t从20分到30分,s从600米增加到1200米,对应图像为
故选:A.
【点评】本题考查了一次折线图像与实际结合的问题,注意正确理解每段时间与路程的变化情况是解题关键.
3.【考点】求自变量的值或函数值、投球问题(实际问题与二次函数)
【分析】根据球弹起后又回到地面时,得到,解方程即可得到答案.
解:球弹起后又回到地面时,即,
解得(不合题意,舍去),,
∴球弹起后又回到地面所花的时间(秒)是2,
故选:D
【点评】此题考查了求二次函数自变量的值,读懂题意,得到方程是解题的关键.
4.【考点】函数图象识别
【分析】根据蓄水池的横断面示意图,可知水的深度增长的速度由慢到快,然后再由快到慢,最后不变,进而求解即可.
解:由蓄水池的横断面示意图可得,
水的深度增长的速度由慢到快,然后再由快到慢,最后不变,
故选:D.
【点评】主要考查了函数图象的读图能力和函数与实际问题结合的应用.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
5.【考点】写出直角坐标系中点的坐标
【分析】根据已知条件,确定平面直角坐标系原点,最后即可求出答案.
解:“车”所在位置的坐标为,
确定点即是平面直角坐标系的原点,且每一格的单位长度是1,
“炮”所在位置的坐标为.
故选:A.
【点评】本题考查了平面直角坐标系,解题的关键在于根据已知条件确定原点.
6.【考点】一次函数图象与坐标轴的交点问题、判断一次函数的增减性
【分析】根据一次函数的性质和各个选项中的条件,可以判断是否正确,从而可以解答本题.
解:∵直线y= 2x+3
∴y随x增大而减小,当y=0时,x=1.5
∵(x1,y1),(x2,y2),(x3,y3)为直线y= 2x+3上的三个点,且x1∴若x1x2>0,则x1,x2同号,但不能确定y1y3的正负,故选项A不符合题意;
若x1x3<0,则x1,x3异号,但不能确定y1y2的正负,故选项B不符合题意;
若x2x3>0,则x2,x3同号,但不能确定y1y3的正负,故选项C不符合题意;
若x2x3<0,则x2,x3异号,则x1,x2同时为负,故y1,y2同时为正,故y1y2>0,故选项D符合题意.
故选:D.
【点评】本题考查一次函数图象上点的坐标特征,解题的关键是明确题意,利用一次函数的性质解答.
7.【考点】坐标与图形、用勾股定理解三角形
【分析】根据学校和体育场的坐标建立直角坐标系,利用勾股定理求出各点到原点的距离,由此得到答案.
解:根据学校和体育场的坐标建立直角坐标系,
超市到原点的距离为,
医院到原点的距离为,
学校到原点的距离为,
体育场到原点的距离为,
故选:A.
【点评】此题考查了根据点坐标确定原点,勾股定理,正确理解点坐标得到原点的位置及正确展望勾股定理的计算是解题的关键.
8.【考点】求一次函数解析式、y=ax +bx+c的最值
【分析】把代入后表示出,再根据最大值求出k,最后把代入即可.
把代入得:
∴
∵的最大值为9
∴,且当时,有最大值,此时
解得
∴直线解析式为
把代入得
故选:B.
【点评】本题考查一次函数上点的特点、二次函数最值,解题的关键是根据的最大值为9求出k的值.
9.【考点】一次函数与几何综合、根据矩形的性质与判定求线段长、相似三角形的判定与性质综合
【分析】先根据矩形的判定与性质可得,从而可得,再根据相似三角形的判定证出,然后根据相似三角形的性质即可得出结论.
解:由题意可知,四边形是矩形,
,
,
,
又,
,
,
,
,
,
整理得:,
故选:B.
【点评】本题考查了矩形的判定与性质、相似三角形的判定与性质、一次函数的几何应用,熟练掌握相似三角形的判定与性质是解题关键.
10.【考点】三元一次方程组的应用、从函数的图象获取信息
【分析】设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟.小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.
解:由图象可知:小州游玩行走的时间为(分钟),小温游玩行走的时间为(分钟);
设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由图象可得:
,
解得:,
∴游玩行走的速度为(米/分),
由于游玩行走速度恒定,则小温游路线①④⑤⑥⑦⑧的路程为,
∴,
∴路线①③⑥⑦⑧各路段路程之和为(米);
故选B.
【点评】本题主要考查三元一次方程组的应用及函数图象,解题的关键是理解题中所给信息,找到它们之间的等量关系.
11.【考点】两直线的交点与二元一次方程组的解
【分析】根据一次函数的交点坐标即可确定以两个一次函数解析式组成的二元一次方程组的解.
解:∵一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),
∴联立y=3x-1与y=kx的方程组的解为:,
即的解为:,
故答案为:.
【点评】本题考查了一次函数与二元一次方程组,熟练掌握一次函数的交点坐标与二元一次方程组的解的关系是解题的关键.
12.【考点】写出直角坐标系中点的坐标
【分析】根据点A、B的坐标可确定原点的位置,再作平面直角坐标系即可,从而可确定点C的坐标.
解:建立平面直角坐标系如图所示:
∴点C的坐标为,
故答案为:.
【点评】本题考查平面直角坐标系、在坐标系中确定点的坐标,根据点A、B的坐标确定原点的位置是解题的关键.
13.【考点】坐标与图形、全等的性质和SAS综合(SAS)、正多边形和圆的综合、求关于原点对称的点的坐标
【分析】如图,延长正六边形的边BM与x轴交于点E,过A作轴于N,连接AO,BO,证明可得三点共线,可得关于O对称,从而可得答案.
解:如图,延长正六边形的边BM与x轴交于点E,过A作轴于N,连接AO,BO,
三个正六边形,O为原点,
同理:
三点共线,
关于O对称,
故答案为:
【点评】本题考查的是坐标与图形的性质,全等三角形的判定与性质,关于原点成中心对称的两个点的坐标特点,正多边形的性质,熟练的应用正多边形的性质解题是解本题的关键.
14.【考点】求一次函数解析式
【分析】分别求出三个函数解析式,然后求出,进行比较即可解答.
解:设过,则有:
,解得:,则;
同理:,
则分别计算,的最大值为值.
故答案为5.
【点评】本题主要考查了求一次函数解析式,掌握待定系数法是解答本题的关键.
15.【考点】求一次函数解析式、其他问题(一次函数的实际应用)
【分析】(1)把点A的坐标代入直线解析式可求解m,然后设直线的函数解析式为,进而根据待定系数法可进行求解函数解析式;
(2)由(1)及题意易得,,则有,然后根据一次函数的性质可进行求解.
(1)解:把点代入,得.
设直线的函数表达式为,把点,代入得
,解得,
∴直线的函数表达式为.
(2)解:∵点在线段上,点在直线上,
∴,,
∴.
∵,
∴的值随的增大而减小,
∴当时,的最大值为.
【点评】本题主要考查一次函数的图象与性质,熟练掌握一次函数的图象与性质是解题的关键.
16.【考点】从函数的图象获取信息、行程问题(一次函数的实际应用)
【分析】(1)根据货车行驶的路程和速度求出a的值;
(2)将(a,0)和(3,150)代入s=kt+b中,待定系数法解出k和b的值即可;
(3)求出汽车和货车到达乙地的时间,作差即可求得答案.
(1)由图中可知,货车a小时走了90km,
∴a=;
(2)设轿车离甲地的路程与时间的函数表达式为s=kt+b,
将(1.5,0)和(3,150)代入得,
,
解得,,
∴轿车离甲地的路程与时间的函数表达式为s=100t-150;
(3)将s=330代入s=100t-150,
解得t=4.8,
两车相遇后,货车还需继续行驶:(h),
到达乙地一共:3+3=6(h),
6-4.8=1.2(h),
∴轿车比货车早1.2h时间到达乙地.
【点评】本题考查了一次函数的应用,主要利用待定系数法求函数解析式,路程、速度、时间三者之间的关系,从图中准确获取信息是解题的关键.
17.【考点】求一次函数解析式、画一次函数图象、其他问题(一次函数的实际应用)
【分析】(1)观察表格数据,的增长量是固定的,故符合一次函数模型,建立模型待定系数法求解析式,画出函数图像即可求解;
(2)根据,代入解析式求得的值即可求解.
(1)(1)选择y=kx+b,将(0,1),(1,2)代入,
得解得
∴y=x+1(0≤x≤5).
(2)当y=5时,x+1=5,
∴x=4.
答:当水位高度达到5米时,进水用时x为4小时.
【点评】本题考查了一次函数的性质,画一次函数图像,求一次函数的解析式,根据题意建立模型是解题的关键.
18.【考点】求一次函数解析式、行程问题(一次函数的实际应用)
【分析】(1)利用待定系数法即可求解;
(2)利用待定系数法求出所在直线的表达式,再列方程组求出交点坐标,即可;
(3)列出方程即可解决.
(1)∵,
∴所在直线的表达式为.
(2)设所在直线的表达式为,
∵,
∴解得
∴.
甲、乙机器人相遇时,即,解得,
∴出发后甲机器人行走分钟,与乙机器人相遇.
(3)设甲机器人行走分钟时到地,地与地距离,
则乙机器人分钟后到地,地与地距离,
由,得.
∴.
答:两地间的距离为600米.
【点评】本题考查了一次函数的图象与性质,用待定系数法可求出函数表达式,要利用方程组的解,求出两个函数的交点坐标,充分应用数形结合思想是解题的关键.
19.【考点】从函数的图象获取信息、求一次函数解析式、其他问题(一次函数的实际应用)
【分析】(1)由图象的交点坐标即可得到解答;
(2)由图象可得点,设方案二的函数表达式为,利用待定系数法即可得到方案二y关于x的函数表达式;
(3)利用图象的位置关系,结合交点的横坐标即可得到结论.
(1)解:由图象可知交点坐标为,即员工生产30件产品时,两种方案付给的报酬一样多;
(2)由图象可得点,设方案二的函数表达式为,
把代入上式,得
解得
∴方案二的函数表达式为.
(3)若每月生产产品件数不足30件,则选择方案二;
若每月生产产品件数就是30件,两种方案报酬相同,可以任选一种;
若每月生产产品件数超过30件,则选择方案一.
【点评】此题考查了从函数图像获取信息、一次函数的应用等知识,从函数图象获取正确信息和掌握待定系数法是解题的关键.
20.【考点】从函数的图象获取信息、行程问题(一次函数的实际应用)
【分析】(1)结合图表可得,根据速度等于路程除以时间,即可解答;
(2)①根据时间=路程÷速度可知妹妹到书吧所用的时间,再根据题意确定a得值即可;
②如图,将妹妹走完全程的图象画出,将和的解析式求出,求两个函数的交点即可.
(1)解:由图可得,
(米/分),
∴哥哥步行速度为100米/分.
(2)①根据妺妺到书吧前的速度为200米/分,
∴妹妹所用时间t为:(min).
∵妹妹比哥哥迟2分钟到书吧,
∴.
②能追上.
如图,根据哥哥的速度没变,可得的解析式的k值相同,妹妹的速度减小但仍大于哥哥的速度,将妹妹的行程图象补充完整,
设所在直线为,将代入,得,
解得,
∴.
∵妺妺的速度是160米/分.
设所在直线为,将代入,得,
解得,
∴.
联立方程,
解得,
∴米,即追上时兄妺俩离家300米远.
【点评】本题考查了一次函数的实际应用(行程问题),从图像中获得正确的信息是解题的关键.
21.【考点】从函数的图象获取信息、行程问题(一次函数的实际应用)
【分析】(1)设出函数解析式,利用待定系数法求出函数解析式,将,代入解析式求出的值即可;
(2)先求出军车的速度,然后分别求出军车到达仓库,和从仓库出发到达基地的时间,用总时间减去两段时间即可得解.
(1)解:设大巴离营地的路程s与所用时间t的函数表达式为,由图象可知,直线过点,
∴,解得:,
∴;
当时:,解得:,
∴;
(2)由图象可知,军车的速度为:,
∴军车到达仓库所用时间为:,
从仓库到达基地所用时间为:,
∴部队官兵在仓库领取物资所用的时间为.
【点评】本题考查一次函数的实际应用.从函数图象上有效的获取信息,正确的求出函数解析式,是解题的关键.
22.【考点】行程问题(一元一次方程的应用)、从函数的图象获取信息
【分析】此题考查函数图象获取信息,一元一次方程的应用,读懂图象中的数据是解本题的关键.
(1)由小明的跑步里程及时间可得档速度,再根据C档比B档快40米/分、B档比A档快40米/分可得B,C档速度;
(2)结合图象求出小丽每段跑步所用时间,再根据总时间即可求解;
(3)由题意可得,此时小丽在跑第三段,所跑时间为(分),可得方程,求解即可.
(1)解:由题意可知,档速度为米/分,
则档速度为米/分,档速度为米/分;
(2)小丽第一段跑步时间为分,
小丽第二段跑步时间为分,
小丽第三段跑步时间为分,
则小丽两次休息时间的总和分;
(3)由题意可得:小丽第二次休息后,在分钟时两人跑步累计里程相等,
此时小丽在跑第三段,所跑时间为:(分)
可得:,
解得:.
23.【考点】求一次函数解析式、已知直线与坐标轴交点求方程的解、点到直线的距离、全等的性质和ASA(AAS)综合(ASA或者AAS)
【分析】本题是三角形综合题,考查了点到直线的距离、全等三角形的判定与性质,待定系数法,一次函数解析式与坐标轴的交点等知识.
(1)分别作,,垂足为E,F,利用证明,得到即可证明直线是点A、B的一条等距线;
(2)根据两点等距线的定义作图,连接中点与组成的直线或者过作的平行线即可;
(3)由可得A、B两点到直线的距离相等,再分两类进行讨论,由待定系数求出直线解析式即可求出点P的坐标.
(1)证明:分别过A,B两点作,垂足分别为E,F.
,
是的中点,
,
在和中,
,
,
即直线是点A,B的一条等距线;
(2)如图,直线就是所有的直线,
(3)设直线的解析式为,
,
∴解得:
∴直线的解析式为.
,
两点到直线的距离相等,
∴或过中点,
如图,当时,可设直线的解析式为,代入得,解得,
∴直线的解析式为,
∴直线与坐标轴的交点为;
②当直线过中点时,
,
∴中点E的坐标为,
∴设直线的函数解析式为,
代入,得,解得:,
∴直线的函数解析式为,
∴直线与坐标轴的交点为.
综上所述,满足条件的点P的坐标为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【备考2025】中考数学真题2022-2024分类精编精练6坐标系与一次函数
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.(2023·浙江·)在平面直角坐标系中,点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2022·浙江温州·)小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图像,能近似刻画s与t之间关系的是( )
A. B.
C. D.
3.(2023·浙江·)一个球从地面竖直向上弹起时的速度为10米/秒,经过(秒)时球距离地面的高度(米)适用公式,那么球弹起后又回到地面所花的时间(秒)是( )
A.5 B.10 C.1 D.2
4.(2023·浙江嘉兴·)下图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )
A. B.
C. D.
5.(2023·浙江台州·)如图是中国象棋棋盘的一部分,建立如图所示的平面直角坐标系,已知“车”所在位置的坐标为,则“炮”所在位置的坐标为( ).
A. B. C. D.
6.(2022·浙江绍兴·)已知为直线上的三个点,且,则以下判断正确的是( ).
A.若,则 B.若,则
C.若,则 D.若,则
7.(2022·浙江金华·)如图是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是,下列各地点中,离原点最近的是( )
A.超市 B.医院 C.体育场 D.学校
8.(2022·浙江舟山·)已知点,在直线(k为常数,)上,若的最大值为9,则c的值为( )
A. B.2 C. D.1
9.(2022·浙江衢州·)西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端(人眼)望点,使视线通过点,记人站立的位置为点,量出长,即可算得物高.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则关于的函数表达式为( )
A. B. C. D.
10.(2023·浙江温州·)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.
【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟.小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.
【问题】路线①③⑥⑦⑧各路段路程之和为( )
A.4200米 B.4800米 C.5200米 D.5400米
二、填空题
11.(2022·浙江杭州·)已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组的解是 .
12.(2023·浙江衢州·)在如图所示的方格纸上建立适当的平面直角坐标系,若点A的坐标为,点B的坐标为,则点C的坐标为 .
13.(2022·浙江丽水·)三个能够重合的正六边形的位置如图.已知B点的坐标是,则A点的坐标是 .
14.(2023·浙江杭州·)在“ “探索一次函数的系数与图像的关系”活动中,老师给出了直角坐标系中的三个点:.同学们画出了经过这三个点中每两个点的一次函数的图像,并得到对应的函数表达式.分别计算,的值,其中最大的值等于 .
三、解答题
15.(2023·浙江温州·)如图,在直角坐标系中,点在直线上,过点A的直线交y轴于点.
(1)求m的值和直线的函数表达式.
(2)若点在线段上,点在直线上,求的最大值.
16.(2022·浙江丽水·)因疫情防控需要,一辆货车先从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地.已知甲、乙两地的路程是,货车行驶时的速度是.两车离甲地的路程与时间的函数图象如图.
(1)求出a的值;
(2)求轿车离甲地的路程与时间的函数表达式;
(3)问轿车比货车早多少时间到达乙地?
17.(2022·浙江绍兴·)一个深为6米的水池积存着少量水,现在打开水阀进水,下表记录了2小时内5个时刻的水位高度,其中x表示进水用时(单位:小时),y表示水位高度(单位:米).
x 0 0.5 1 1.5 2
y 1 1.5 2 2.5 3
为了描述水池水位高度与进水用时的关系,现有以下三种函数模型供选择:(),y=ax2+bx+c (),().
(1)在平面直角坐标系中描出表中数据对应的点,再选出最符合实际的函数模型,求出相应的函数表达式,并画出这个函数的图像.
(2)当水位高度达到5米时,求进水用时x.
18.(2023·浙江绍兴·)一条笔直的路上依次有三地,其中两地相距1000米.甲、乙两机器人分别从两地同时出发,去目的地,匀速而行.图中分别表示甲、乙机器人离地的距离(米)与行走时间(分钟)的函数关系图象.
(1)求所在直线的表达式.
(2)出发后甲机器人行走多少时间,与乙机器人相遇?
(3)甲机器人到地后,再经过1分钟乙机器人也到地,求两地间的距离.
19.(2023·浙江·)我市“共富工坊”问海借力,某公司产品销售量得到大幅提升.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.看图解答下列问题:
(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2)求方案二y关于x的函数表达式;
(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.
20.(2023·浙江金华·)兄妹俩放学后沿图1中的马路从学校出发,到书吧看书后回家,哥哥步行先出发,途中速度保持不变;妺妺骑车,到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程(米)与哥哥离开学校的时间(分)的函数关系.
(1)求哥哥步行的速度.
(2)已知妺妺比哥哥迟2分钟到书吧.
①求图中的值;
②妺妺在书吧待了10分钟后回家,速度是哥哥的倍,能否在哥哥到家前追上哥哥?若能,求追上时兄妺俩离家还有多远;若不能,说明理由.
21.(2023·浙江宁波·)某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学,上午8:00,军车在离营地的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.
(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值,
(2)求部队官兵在仓库领取物资所用的时间.
22.(2024·浙江·)小明和小丽在跑步机上慢跑锻炼.小明先跑,10分钟后小丽才开始跑,小丽跑步时中间休息了两次.跑步机上C档比B档快40米/分、B档比A档快40米/分.小明与小丽的跑步相关信息如表所示,跑步累计里程s(米)与小明跑步时间t(分)的函数关系如图所示.
时间 里程分段 速度档 跑步里程
小明 不分段 A档 4000米
小丽 第一段 B档 1800米
第一次休息
第二段 B档 1200米
第二次休息
第三段 C档 1600米
(1)求A,B,C各档速度(单位:米/分);
(2)求小丽两次休息时间的总和(单位:分);
(3)小丽第二次休息后,在a分钟时两人跑步累计里程相等,求a的值.
23.(2023·浙江绍兴·)如果两点到一条直线的距离相等,则称该直线为“两点的等距线”.
(1) 如图1,直线经过线段的中点P,试说明直线是点A,B的一条等距线.
(2)如图2,是正方形网格中的三个格点,请在网格中作出所有的直线m,使直线m过点C且直线m是“两点的等距线”.
(3)如图3,中,,则在坐标轴上是否存在点P,使?若存在,试求出点P的坐标;若不存在,请说明理由.
参考答案
1.【考点】判断点所在的象限
【分析】根据点坐标分别判断出横坐标和纵坐标的符号,从而就可以判断改点所在的象限.
解:,
,,
满足第二象限的条件.
故选:B.
【点评】本题考查的是平面直角坐标系中点的坐标以及象限知识,解题的关键在于熟练掌握各个象限的横纵坐标点的符号特点.
2.【考点】函数图象识别
【分析】分别对每段时间的路程与时间的变化情况进行分析,画出路程与时间图像,再与选项对比判断即可.
解:对各段时间与路程的关系进行分析如下:
从家到凉亭,用时10分钟,路程600米,s从0增加到600米,t从0到10分,对应图像为
在凉亭休息10分钟,t从10分到20分,s保持600米不变,对应图像为
从凉亭到公园,用时间10分钟,路程600米,t从20分到30分,s从600米增加到1200米,对应图像为
故选:A.
【点评】本题考查了一次折线图像与实际结合的问题,注意正确理解每段时间与路程的变化情况是解题关键.
3.【考点】求自变量的值或函数值、投球问题(实际问题与二次函数)
【分析】根据球弹起后又回到地面时,得到,解方程即可得到答案.
解:球弹起后又回到地面时,即,
解得(不合题意,舍去),,
∴球弹起后又回到地面所花的时间(秒)是2,
故选:D
【点评】此题考查了求二次函数自变量的值,读懂题意,得到方程是解题的关键.
4.【考点】函数图象识别
【分析】根据蓄水池的横断面示意图,可知水的深度增长的速度由慢到快,然后再由快到慢,最后不变,进而求解即可.
解:由蓄水池的横断面示意图可得,
水的深度增长的速度由慢到快,然后再由快到慢,最后不变,
故选:D.
【点评】主要考查了函数图象的读图能力和函数与实际问题结合的应用.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
5.【考点】写出直角坐标系中点的坐标
【分析】根据已知条件,确定平面直角坐标系原点,最后即可求出答案.
解:“车”所在位置的坐标为,
确定点即是平面直角坐标系的原点,且每一格的单位长度是1,
“炮”所在位置的坐标为.
故选:A.
【点评】本题考查了平面直角坐标系,解题的关键在于根据已知条件确定原点.
6.【考点】一次函数图象与坐标轴的交点问题、判断一次函数的增减性
【分析】根据一次函数的性质和各个选项中的条件,可以判断是否正确,从而可以解答本题.
解:∵直线y= 2x+3
∴y随x增大而减小,当y=0时,x=1.5
∵(x1,y1),(x2,y2),(x3,y3)为直线y= 2x+3上的三个点,且x1
若x1x3<0,则x1,x3异号,但不能确定y1y2的正负,故选项B不符合题意;
若x2x3>0,则x2,x3同号,但不能确定y1y3的正负,故选项C不符合题意;
若x2x3<0,则x2,x3异号,则x1,x2同时为负,故y1,y2同时为正,故y1y2>0,故选项D符合题意.
故选:D.
【点评】本题考查一次函数图象上点的坐标特征,解题的关键是明确题意,利用一次函数的性质解答.
7.【考点】坐标与图形、用勾股定理解三角形
【分析】根据学校和体育场的坐标建立直角坐标系,利用勾股定理求出各点到原点的距离,由此得到答案.
解:根据学校和体育场的坐标建立直角坐标系,
超市到原点的距离为,
医院到原点的距离为,
学校到原点的距离为,
体育场到原点的距离为,
故选:A.
【点评】此题考查了根据点坐标确定原点,勾股定理,正确理解点坐标得到原点的位置及正确展望勾股定理的计算是解题的关键.
8.【考点】求一次函数解析式、y=ax +bx+c的最值
【分析】把代入后表示出,再根据最大值求出k,最后把代入即可.
把代入得:
∴
∵的最大值为9
∴,且当时,有最大值,此时
解得
∴直线解析式为
把代入得
故选:B.
【点评】本题考查一次函数上点的特点、二次函数最值,解题的关键是根据的最大值为9求出k的值.
9.【考点】一次函数与几何综合、根据矩形的性质与判定求线段长、相似三角形的判定与性质综合
【分析】先根据矩形的判定与性质可得,从而可得,再根据相似三角形的判定证出,然后根据相似三角形的性质即可得出结论.
解:由题意可知,四边形是矩形,
,
,
,
又,
,
,
,
,
,
整理得:,
故选:B.
【点评】本题考查了矩形的判定与性质、相似三角形的判定与性质、一次函数的几何应用,熟练掌握相似三角形的判定与性质是解题关键.
10.【考点】三元一次方程组的应用、从函数的图象获取信息
【分析】设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟.小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.
解:由图象可知:小州游玩行走的时间为(分钟),小温游玩行走的时间为(分钟);
设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由图象可得:
,
解得:,
∴游玩行走的速度为(米/分),
由于游玩行走速度恒定,则小温游路线①④⑤⑥⑦⑧的路程为,
∴,
∴路线①③⑥⑦⑧各路段路程之和为(米);
故选B.
【点评】本题主要考查三元一次方程组的应用及函数图象,解题的关键是理解题中所给信息,找到它们之间的等量关系.
11.【考点】两直线的交点与二元一次方程组的解
【分析】根据一次函数的交点坐标即可确定以两个一次函数解析式组成的二元一次方程组的解.
解:∵一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),
∴联立y=3x-1与y=kx的方程组的解为:,
即的解为:,
故答案为:.
【点评】本题考查了一次函数与二元一次方程组,熟练掌握一次函数的交点坐标与二元一次方程组的解的关系是解题的关键.
12.【考点】写出直角坐标系中点的坐标
【分析】根据点A、B的坐标可确定原点的位置,再作平面直角坐标系即可,从而可确定点C的坐标.
解:建立平面直角坐标系如图所示:
∴点C的坐标为,
故答案为:.
【点评】本题考查平面直角坐标系、在坐标系中确定点的坐标,根据点A、B的坐标确定原点的位置是解题的关键.
13.【考点】坐标与图形、全等的性质和SAS综合(SAS)、正多边形和圆的综合、求关于原点对称的点的坐标
【分析】如图,延长正六边形的边BM与x轴交于点E,过A作轴于N,连接AO,BO,证明可得三点共线,可得关于O对称,从而可得答案.
解:如图,延长正六边形的边BM与x轴交于点E,过A作轴于N,连接AO,BO,
三个正六边形,O为原点,
同理:
三点共线,
关于O对称,
故答案为:
【点评】本题考查的是坐标与图形的性质,全等三角形的判定与性质,关于原点成中心对称的两个点的坐标特点,正多边形的性质,熟练的应用正多边形的性质解题是解本题的关键.
14.【考点】求一次函数解析式
【分析】分别求出三个函数解析式,然后求出,进行比较即可解答.
解:设过,则有:
,解得:,则;
同理:,
则分别计算,的最大值为值.
故答案为5.
【点评】本题主要考查了求一次函数解析式,掌握待定系数法是解答本题的关键.
15.【考点】求一次函数解析式、其他问题(一次函数的实际应用)
【分析】(1)把点A的坐标代入直线解析式可求解m,然后设直线的函数解析式为,进而根据待定系数法可进行求解函数解析式;
(2)由(1)及题意易得,,则有,然后根据一次函数的性质可进行求解.
(1)解:把点代入,得.
设直线的函数表达式为,把点,代入得
,解得,
∴直线的函数表达式为.
(2)解:∵点在线段上,点在直线上,
∴,,
∴.
∵,
∴的值随的增大而减小,
∴当时,的最大值为.
【点评】本题主要考查一次函数的图象与性质,熟练掌握一次函数的图象与性质是解题的关键.
16.【考点】从函数的图象获取信息、行程问题(一次函数的实际应用)
【分析】(1)根据货车行驶的路程和速度求出a的值;
(2)将(a,0)和(3,150)代入s=kt+b中,待定系数法解出k和b的值即可;
(3)求出汽车和货车到达乙地的时间,作差即可求得答案.
(1)由图中可知,货车a小时走了90km,
∴a=;
(2)设轿车离甲地的路程与时间的函数表达式为s=kt+b,
将(1.5,0)和(3,150)代入得,
,
解得,,
∴轿车离甲地的路程与时间的函数表达式为s=100t-150;
(3)将s=330代入s=100t-150,
解得t=4.8,
两车相遇后,货车还需继续行驶:(h),
到达乙地一共:3+3=6(h),
6-4.8=1.2(h),
∴轿车比货车早1.2h时间到达乙地.
【点评】本题考查了一次函数的应用,主要利用待定系数法求函数解析式,路程、速度、时间三者之间的关系,从图中准确获取信息是解题的关键.
17.【考点】求一次函数解析式、画一次函数图象、其他问题(一次函数的实际应用)
【分析】(1)观察表格数据,的增长量是固定的,故符合一次函数模型,建立模型待定系数法求解析式,画出函数图像即可求解;
(2)根据,代入解析式求得的值即可求解.
(1)(1)选择y=kx+b,将(0,1),(1,2)代入,
得解得
∴y=x+1(0≤x≤5).
(2)当y=5时,x+1=5,
∴x=4.
答:当水位高度达到5米时,进水用时x为4小时.
【点评】本题考查了一次函数的性质,画一次函数图像,求一次函数的解析式,根据题意建立模型是解题的关键.
18.【考点】求一次函数解析式、行程问题(一次函数的实际应用)
【分析】(1)利用待定系数法即可求解;
(2)利用待定系数法求出所在直线的表达式,再列方程组求出交点坐标,即可;
(3)列出方程即可解决.
(1)∵,
∴所在直线的表达式为.
(2)设所在直线的表达式为,
∵,
∴解得
∴.
甲、乙机器人相遇时,即,解得,
∴出发后甲机器人行走分钟,与乙机器人相遇.
(3)设甲机器人行走分钟时到地,地与地距离,
则乙机器人分钟后到地,地与地距离,
由,得.
∴.
答:两地间的距离为600米.
【点评】本题考查了一次函数的图象与性质,用待定系数法可求出函数表达式,要利用方程组的解,求出两个函数的交点坐标,充分应用数形结合思想是解题的关键.
19.【考点】从函数的图象获取信息、求一次函数解析式、其他问题(一次函数的实际应用)
【分析】(1)由图象的交点坐标即可得到解答;
(2)由图象可得点,设方案二的函数表达式为,利用待定系数法即可得到方案二y关于x的函数表达式;
(3)利用图象的位置关系,结合交点的横坐标即可得到结论.
(1)解:由图象可知交点坐标为,即员工生产30件产品时,两种方案付给的报酬一样多;
(2)由图象可得点,设方案二的函数表达式为,
把代入上式,得
解得
∴方案二的函数表达式为.
(3)若每月生产产品件数不足30件,则选择方案二;
若每月生产产品件数就是30件,两种方案报酬相同,可以任选一种;
若每月生产产品件数超过30件,则选择方案一.
【点评】此题考查了从函数图像获取信息、一次函数的应用等知识,从函数图象获取正确信息和掌握待定系数法是解题的关键.
20.【考点】从函数的图象获取信息、行程问题(一次函数的实际应用)
【分析】(1)结合图表可得,根据速度等于路程除以时间,即可解答;
(2)①根据时间=路程÷速度可知妹妹到书吧所用的时间,再根据题意确定a得值即可;
②如图,将妹妹走完全程的图象画出,将和的解析式求出,求两个函数的交点即可.
(1)解:由图可得,
(米/分),
∴哥哥步行速度为100米/分.
(2)①根据妺妺到书吧前的速度为200米/分,
∴妹妹所用时间t为:(min).
∵妹妹比哥哥迟2分钟到书吧,
∴.
②能追上.
如图,根据哥哥的速度没变,可得的解析式的k值相同,妹妹的速度减小但仍大于哥哥的速度,将妹妹的行程图象补充完整,
设所在直线为,将代入,得,
解得,
∴.
∵妺妺的速度是160米/分.
设所在直线为,将代入,得,
解得,
∴.
联立方程,
解得,
∴米,即追上时兄妺俩离家300米远.
【点评】本题考查了一次函数的实际应用(行程问题),从图像中获得正确的信息是解题的关键.
21.【考点】从函数的图象获取信息、行程问题(一次函数的实际应用)
【分析】(1)设出函数解析式,利用待定系数法求出函数解析式,将,代入解析式求出的值即可;
(2)先求出军车的速度,然后分别求出军车到达仓库,和从仓库出发到达基地的时间,用总时间减去两段时间即可得解.
(1)解:设大巴离营地的路程s与所用时间t的函数表达式为,由图象可知,直线过点,
∴,解得:,
∴;
当时:,解得:,
∴;
(2)由图象可知,军车的速度为:,
∴军车到达仓库所用时间为:,
从仓库到达基地所用时间为:,
∴部队官兵在仓库领取物资所用的时间为.
【点评】本题考查一次函数的实际应用.从函数图象上有效的获取信息,正确的求出函数解析式,是解题的关键.
22.【考点】行程问题(一元一次方程的应用)、从函数的图象获取信息
【分析】此题考查函数图象获取信息,一元一次方程的应用,读懂图象中的数据是解本题的关键.
(1)由小明的跑步里程及时间可得档速度,再根据C档比B档快40米/分、B档比A档快40米/分可得B,C档速度;
(2)结合图象求出小丽每段跑步所用时间,再根据总时间即可求解;
(3)由题意可得,此时小丽在跑第三段,所跑时间为(分),可得方程,求解即可.
(1)解:由题意可知,档速度为米/分,
则档速度为米/分,档速度为米/分;
(2)小丽第一段跑步时间为分,
小丽第二段跑步时间为分,
小丽第三段跑步时间为分,
则小丽两次休息时间的总和分;
(3)由题意可得:小丽第二次休息后,在分钟时两人跑步累计里程相等,
此时小丽在跑第三段,所跑时间为:(分)
可得:,
解得:.
23.【考点】求一次函数解析式、已知直线与坐标轴交点求方程的解、点到直线的距离、全等的性质和ASA(AAS)综合(ASA或者AAS)
【分析】本题是三角形综合题,考查了点到直线的距离、全等三角形的判定与性质,待定系数法,一次函数解析式与坐标轴的交点等知识.
(1)分别作,,垂足为E,F,利用证明,得到即可证明直线是点A、B的一条等距线;
(2)根据两点等距线的定义作图,连接中点与组成的直线或者过作的平行线即可;
(3)由可得A、B两点到直线的距离相等,再分两类进行讨论,由待定系数求出直线解析式即可求出点P的坐标.
(1)证明:分别过A,B两点作,垂足分别为E,F.
,
是的中点,
,
在和中,
,
,
即直线是点A,B的一条等距线;
(2)如图,直线就是所有的直线,
(3)设直线的解析式为,
,
∴解得:
∴直线的解析式为.
,
两点到直线的距离相等,
∴或过中点,
如图,当时,可设直线的解析式为,代入得,解得,
∴直线的解析式为,
∴直线与坐标轴的交点为;
②当直线过中点时,
,
∴中点E的坐标为,
∴设直线的函数解析式为,
代入,得,解得:,
∴直线的函数解析式为,
∴直线与坐标轴的交点为.
综上所述,满足条件的点P的坐标为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
