2024-2025学年八年级下学期数学(北师大版)期中考试(答案+解析)
文档属性
| 名称 | 2024-2025学年八年级下学期数学(北师大版)期中考试(答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 322.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-04 21:53:41 | ||
图片预览

文档简介
保密★启用前
2024-2025学年八年级下册期中考试(北师大版)
数学
考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一个符合题目要求)
1.用反证法证明命题“在直角三角形中,至少有一个锐角不大于”时,首先应假设这个直角三角形中( )
A.两个锐角都大于 B.两个锐角都小于
C.两个锐角都不大于 D.两个锐角都等于
2.下列等式从左到右的变形,属于因式分解的是( )
A. B.
C. D.
3.若一次函数的图象如图所示,则关于x的不等式的解集是( )
A. B. C. D.
4.如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC长是( )
A.7 B.6 C.5 D.4
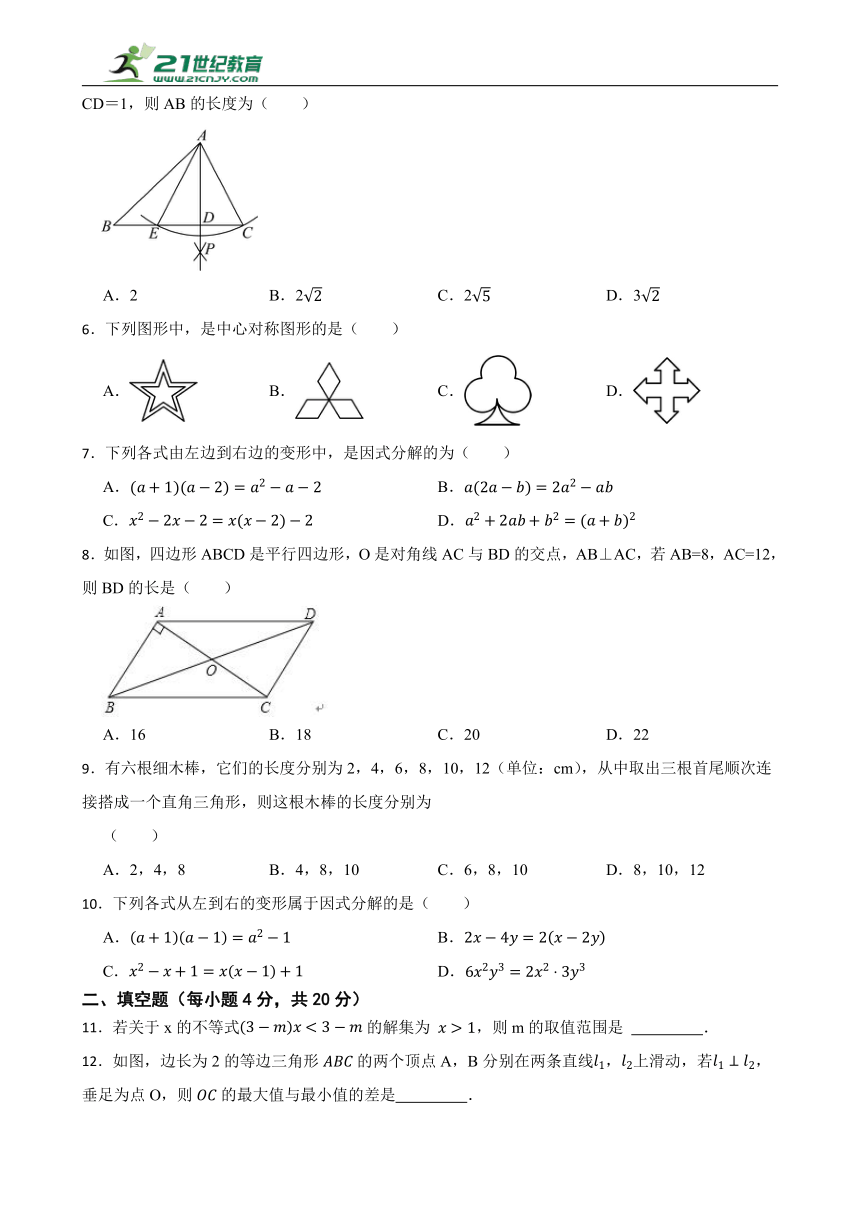
5.如图,在△ABC中,以点A为圆心,AC的长为半径作弧,与BC交于点E,分别以点E,C为圆心,大于EC的长为半径作弧,两弧相交于点P,作射线AP交BC于点D.若∠B=45°,AC=,CD=1,则AB的长度为( )
A.2 B.2 C.2 D.3
6.下列图形中,是中心对称图形的是( )
A. B. C. D.
7.下列各式由左边到右边的变形中,是因式分解的为( )
A. B.
C. D.
8.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.16 B.18 C.20 D.22
9.有六根细木棒,它们的长度分别为2,4,6,8,10,12(单位:cm),从中取出三根首尾顺次连接搭成一个直角三角形,则这根木棒的长度分别为
( )
A.2,4,8 B.4,8,10 C.6,8,10 D.8,10,12
10.下列各式从左到右的变形属于因式分解的是( )
A. B.
C. D.
二、填空题(每小题4分,共20分)
11.若关于x的不等式的解集为 ,则m的取值范围是 .
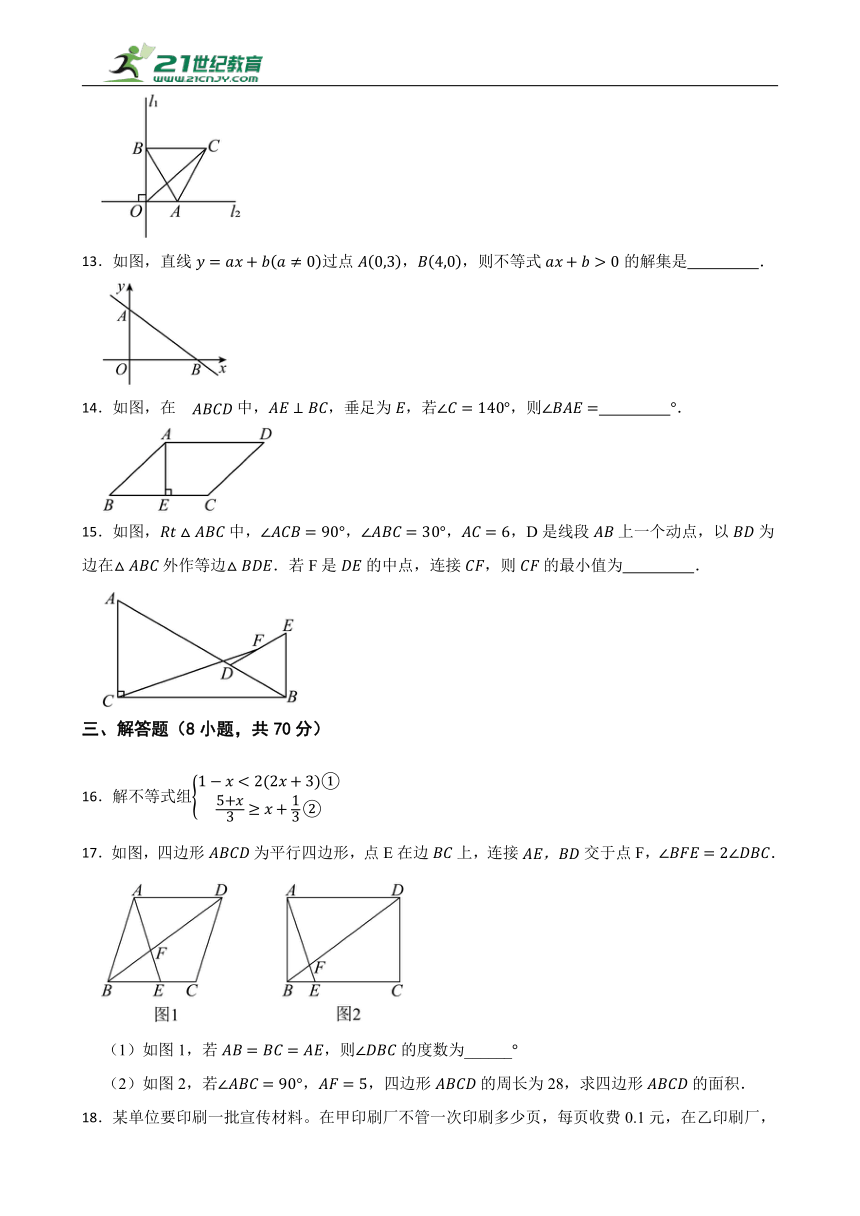
12.如图,边长为2的等边三角形的两个顶点A,B分别在两条直线,上滑动,若,垂足为点O,则的最大值与最小值的差是 .
13.如图,直线过点,,则不等式的解集是 .
14.如图,在中,,垂足为,若,则 .
15.如图,中,,,,D是线段上一个动点,以为边在外作等边.若F是的中点,连接,则的最小值为 .
三、解答题(8小题,共70分)
16.解不等式组
17.如图,四边形为平行四边形,点E在边上,连接交于点F,.
(1)如图1,若,则的度数为______
(2)如图2,若,,四边形的周长为28,求四边形的面积.
18.某单位要印刷一批宣传材料。在甲印刷厂不管一次印刷多少页,每页收费0.1元,在乙印刷厂,一次印刷页数不超过20时,每页收费0.12元,一次印刷页数超过20时,超过部分每页收费0.09元,设该单位需要印刷宣传材料的页数为x(x>20且x是整数),在甲印刷厂实际付费为(元),在乙印刷厂实际收费为(元)
(1)分别写出与x的函数关系式;
(2)你认为选择哪家印刷厂印刷这些宣传材料较好?为什么?
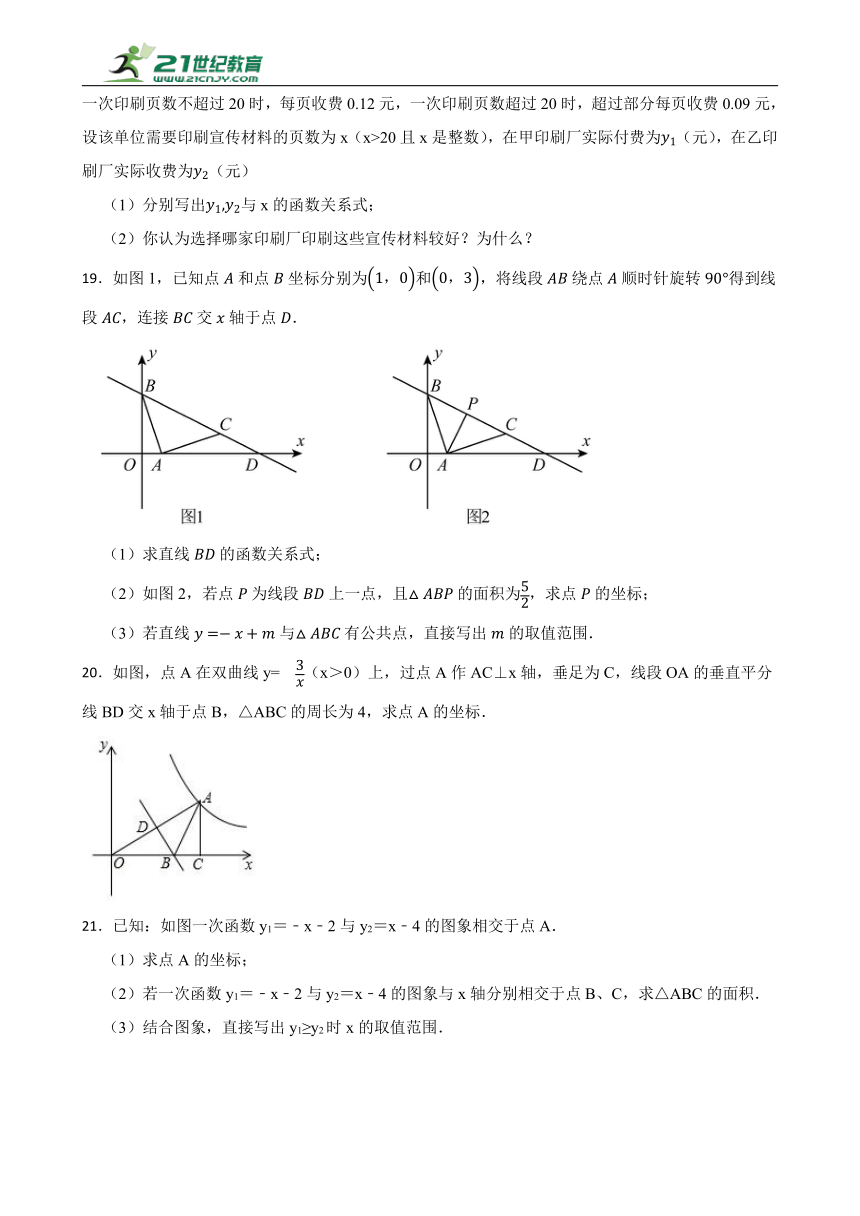
19.如图1,已知点和点坐标分别为和,将线段绕点顺时针旋转得到线段,连接交轴于点.
(1)求直线的函数关系式;
(2)如图2,若点为线段上一点,且的面积为,求点的坐标;
(3)若直线与有公共点,直接写出的取值范围.
20.如图,点A在双曲线y= (x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.
21.已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
22.在一次数学研究性学习中,小敏将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=6cm,
AC=DF=8cm,并进行如下研究活动,
探究问题:
将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
发现问题:
(1)图2中的四边形ABDE是平行四边形吗?请说明理由.
解决问题:
(2)当纸片DEF平移到某一位置时,小敏发现四边形ABDE为矩形(如图3),求AF的长.
23.阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得.又因为,所以关于x的方程的解为.
(1)理解应用:方程的解为: , ;
(2)知识迁移:若关于x的方程的解为,求的值;
(3)拓展提升:若关于x的方程的解为,求的值.
答案解析部分
1.A
解:用反证法证明命题“在直角三角形中,至少有一个锐角不大于”时,
应先假设两个锐角都大于45°.
故选:A.
顾名思义,反证法就是取原题设的相反条件进行论证.
2.C
3.C
解:观察图象可知:直线经过点(1,0)、(3,4)
∴当y=0时,x=1; 当y=4时,x=3;
∴关于x的不等式0<kx+b<4的解集为1<x<3.
故答案为:C.
根据函数值在0~4之间,结合函数图象求出x的范围.
4.D
解:∵DE=3,AB=6,
∴△ABD的面积为=9,
∵S△ABC=15,
∴△ADC的面积=15﹣9=6,
∵AD平分∠BAC,DE⊥AB于E,
∴AC边上的高=DE=3,
∴AC=6×2÷3=4,
故选D.
先求出△ABD的面积,再得出△ADC的面积,最后根据角平分线上的点到角的两边的距离相等可得AC边上的高,从而得解.
5.B
6.D
7.D
8.C
解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选C.
由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
9.C
根据勾股定理的逆定理进行分析,从而得到答案.
由勾股定理的逆定理分析得,只有C中有62+82=102,
故选C.
本题考查了直角三角形的判定
10.B
解:A、,属于整式乘法;
B、,属于因式分解;
C、,没把一个多项式转化成几个整式积的形式,不属于因式分解;
D、,等式左边不是多项式,不属于因式分解;
故答案为:B.
利用因式分解的定义(因式分解是把一个多项式转化成几个整式乘积的形式)逐个分析求解即可.
11.
12.2
13.
14.
15.9
16.解:解不等式①,得:,
解不等式②,得:,
∴原不等式组的解集为.
先分别求出每个不等式的解集,再找到它们的公共部分即可.
17.(1);
(2)四边形的面积为.
18.(1),;
(2)当时,甲、乙两个印刷厂收费相同,当时,甲印刷厂费用少,当 时,乙印刷厂费用少.
19.(1)
(2)
(3)
20.解:设A(a, ),
∵BD垂直平分OA,
∴BA=BO,
∵△ABC的周长为4,即AB+BC+AC=4,
∴OC+AC=4,
∴a+ =4,
解得a=1或a=3,
当A点为(1,3)时,AC=3,
∵△ABC的周长为4,
∴AB+BC=1,
有三角形的两边之和大于第三边,点A(1,3)不符合题意。
∴A点坐标为(3,1).
根据反比例函数图象上点的坐标特征,设设A(a, ),根据线段垂直平分线的性质得BA=BO,由于AB+BC+AC=4,则OC+AC=4,即a+ =4,然后解方程求出a即可得到A点坐标.
21.(1)(1,﹣3);(2)9;(3)x≤1
22.(1)解:四边形是平行四边形.
证明:,
,,,
四边形是平行四边形;
(2)解:如图1,连接交于点,
四边形为矩形,,
设,则,,
在中,,
,解得:,cm.
(1)证明AB和DE平行且相等,可得 四边形ABDE是平行四边形 。
(2)根据矩形的对角线相等且互相平分得出OA=OD=OB=OE,设AF=X,根据勾股定理列方程求出X即可。
23.(1)5,
(2)
(3)
2024-2025学年八年级下册期中考试(北师大版)
数学
考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一个符合题目要求)
1.用反证法证明命题“在直角三角形中,至少有一个锐角不大于”时,首先应假设这个直角三角形中( )
A.两个锐角都大于 B.两个锐角都小于
C.两个锐角都不大于 D.两个锐角都等于
2.下列等式从左到右的变形,属于因式分解的是( )
A. B.
C. D.
3.若一次函数的图象如图所示,则关于x的不等式的解集是( )
A. B. C. D.
4.如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC长是( )
A.7 B.6 C.5 D.4
5.如图,在△ABC中,以点A为圆心,AC的长为半径作弧,与BC交于点E,分别以点E,C为圆心,大于EC的长为半径作弧,两弧相交于点P,作射线AP交BC于点D.若∠B=45°,AC=,CD=1,则AB的长度为( )
A.2 B.2 C.2 D.3
6.下列图形中,是中心对称图形的是( )
A. B. C. D.
7.下列各式由左边到右边的变形中,是因式分解的为( )
A. B.
C. D.
8.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.16 B.18 C.20 D.22
9.有六根细木棒,它们的长度分别为2,4,6,8,10,12(单位:cm),从中取出三根首尾顺次连接搭成一个直角三角形,则这根木棒的长度分别为
( )
A.2,4,8 B.4,8,10 C.6,8,10 D.8,10,12
10.下列各式从左到右的变形属于因式分解的是( )
A. B.
C. D.
二、填空题(每小题4分,共20分)
11.若关于x的不等式的解集为 ,则m的取值范围是 .
12.如图,边长为2的等边三角形的两个顶点A,B分别在两条直线,上滑动,若,垂足为点O,则的最大值与最小值的差是 .
13.如图,直线过点,,则不等式的解集是 .
14.如图,在中,,垂足为,若,则 .
15.如图,中,,,,D是线段上一个动点,以为边在外作等边.若F是的中点,连接,则的最小值为 .
三、解答题(8小题,共70分)
16.解不等式组
17.如图,四边形为平行四边形,点E在边上,连接交于点F,.
(1)如图1,若,则的度数为______
(2)如图2,若,,四边形的周长为28,求四边形的面积.
18.某单位要印刷一批宣传材料。在甲印刷厂不管一次印刷多少页,每页收费0.1元,在乙印刷厂,一次印刷页数不超过20时,每页收费0.12元,一次印刷页数超过20时,超过部分每页收费0.09元,设该单位需要印刷宣传材料的页数为x(x>20且x是整数),在甲印刷厂实际付费为(元),在乙印刷厂实际收费为(元)
(1)分别写出与x的函数关系式;
(2)你认为选择哪家印刷厂印刷这些宣传材料较好?为什么?
19.如图1,已知点和点坐标分别为和,将线段绕点顺时针旋转得到线段,连接交轴于点.
(1)求直线的函数关系式;
(2)如图2,若点为线段上一点,且的面积为,求点的坐标;
(3)若直线与有公共点,直接写出的取值范围.
20.如图,点A在双曲线y= (x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.
21.已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
22.在一次数学研究性学习中,小敏将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=6cm,
AC=DF=8cm,并进行如下研究活动,
探究问题:
将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
发现问题:
(1)图2中的四边形ABDE是平行四边形吗?请说明理由.
解决问题:
(2)当纸片DEF平移到某一位置时,小敏发现四边形ABDE为矩形(如图3),求AF的长.
23.阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得.又因为,所以关于x的方程的解为.
(1)理解应用:方程的解为: , ;
(2)知识迁移:若关于x的方程的解为,求的值;
(3)拓展提升:若关于x的方程的解为,求的值.
答案解析部分
1.A
解:用反证法证明命题“在直角三角形中,至少有一个锐角不大于”时,
应先假设两个锐角都大于45°.
故选:A.
顾名思义,反证法就是取原题设的相反条件进行论证.
2.C
3.C
解:观察图象可知:直线经过点(1,0)、(3,4)
∴当y=0时,x=1; 当y=4时,x=3;
∴关于x的不等式0<kx+b<4的解集为1<x<3.
故答案为:C.
根据函数值在0~4之间,结合函数图象求出x的范围.
4.D
解:∵DE=3,AB=6,
∴△ABD的面积为=9,
∵S△ABC=15,
∴△ADC的面积=15﹣9=6,
∵AD平分∠BAC,DE⊥AB于E,
∴AC边上的高=DE=3,
∴AC=6×2÷3=4,
故选D.
先求出△ABD的面积,再得出△ADC的面积,最后根据角平分线上的点到角的两边的距离相等可得AC边上的高,从而得解.
5.B
6.D
7.D
8.C
解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选C.
由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
9.C
根据勾股定理的逆定理进行分析,从而得到答案.
由勾股定理的逆定理分析得,只有C中有62+82=102,
故选C.
本题考查了直角三角形的判定
10.B
解:A、,属于整式乘法;
B、,属于因式分解;
C、,没把一个多项式转化成几个整式积的形式,不属于因式分解;
D、,等式左边不是多项式,不属于因式分解;
故答案为:B.
利用因式分解的定义(因式分解是把一个多项式转化成几个整式乘积的形式)逐个分析求解即可.
11.
12.2
13.
14.
15.9
16.解:解不等式①,得:,
解不等式②,得:,
∴原不等式组的解集为.
先分别求出每个不等式的解集,再找到它们的公共部分即可.
17.(1);
(2)四边形的面积为.
18.(1),;
(2)当时,甲、乙两个印刷厂收费相同,当时,甲印刷厂费用少,当 时,乙印刷厂费用少.
19.(1)
(2)
(3)
20.解:设A(a, ),
∵BD垂直平分OA,
∴BA=BO,
∵△ABC的周长为4,即AB+BC+AC=4,
∴OC+AC=4,
∴a+ =4,
解得a=1或a=3,
当A点为(1,3)时,AC=3,
∵△ABC的周长为4,
∴AB+BC=1,
有三角形的两边之和大于第三边,点A(1,3)不符合题意。
∴A点坐标为(3,1).
根据反比例函数图象上点的坐标特征,设设A(a, ),根据线段垂直平分线的性质得BA=BO,由于AB+BC+AC=4,则OC+AC=4,即a+ =4,然后解方程求出a即可得到A点坐标.
21.(1)(1,﹣3);(2)9;(3)x≤1
22.(1)解:四边形是平行四边形.
证明:,
,,,
四边形是平行四边形;
(2)解:如图1,连接交于点,
四边形为矩形,,
设,则,,
在中,,
,解得:,cm.
(1)证明AB和DE平行且相等,可得 四边形ABDE是平行四边形 。
(2)根据矩形的对角线相等且互相平分得出OA=OD=OB=OE,设AF=X,根据勾股定理列方程求出X即可。
23.(1)5,
(2)
(3)
同课章节目录
