第二十七章 相似 素养提升(含答案)2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 第二十七章 相似 素养提升(含答案)2024-2025学年数学人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 379.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-04 21:46:12 | ||
图片预览


文档简介
第二十七章相似(素养提升 )
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.两个相似三角形的周长比是则其相似比是( )
A. B. C. D.
2.下列各组线段中,不是成比例线段的是( )
A. 3,6,2,4 B. 4,6,5,10
C. 1,,, D. 2,,,
3.如图,四边形ABCD∽四边形EFGH,,,,则等于
A. B. C. D.
4.如图,AB与CD相交于点O,添加一个条件,不能判断∽的是
A. B. C. D.
5.如图,在平面直角坐标系xOy中,以原点O为位似中心,把线段AB放大后得到线段若点,,,则点A的对应点C的坐标是
A. B. C. D.
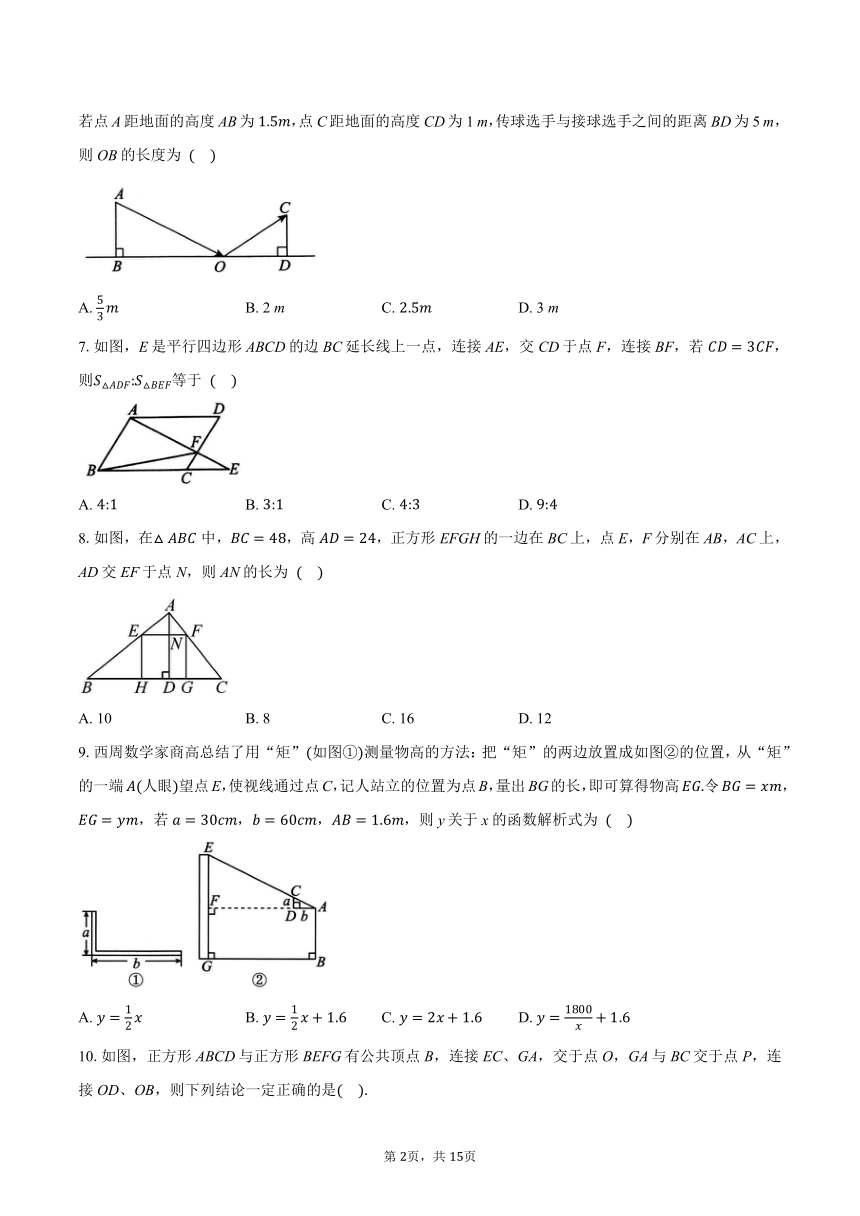
6.击地传球是篮球运动中的一种传球方式,利用击地传球可以有效地躲避对手的拦截.传球选手从点A处将球传出,经地面点O处反弹后被接球选手在点C处接住,将球所经过的路径视为直线,此时若点A距地面的高度AB为,点C距地面的高度CD为1 m,传球选手与接球选手之间的距离BD为5 m,则OB的长度为
A. B. 2 m C. D. 3 m
7.如图,E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF,若,则等于
A. B. C. D.
8.如图,在中,,高,正方形EFGH的一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为
A. 10 B. 8 C. 16 D. 12
9.西周数学家商高总结了用“矩”如图①测量物高的方法:把“矩”的两边放置成如图②的位置,从“矩”的一端人眼望点E,使视线通过点C,记人站立的位置为点B,量出BG的长,即可算得物高令,,若,,,则y关于x的函数解析式为
A. B. C. D.
10.如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是
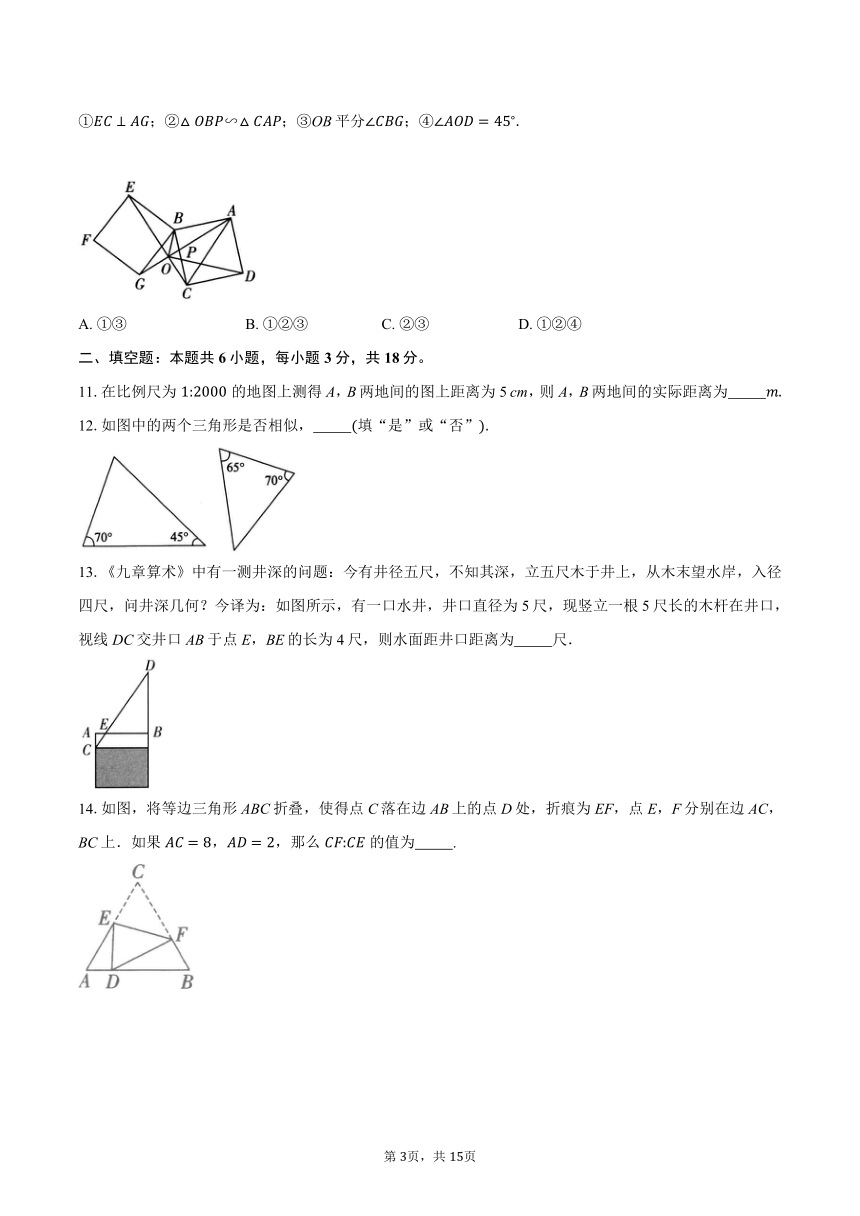
①;②∽;③OB平分;④
A. ①③ B. ①②③ C. ②③ D. ①②④
二、填空题:本题共6小题,每小题3分,共18分。
11.在比例尺为的地图上测得A,B两地间的图上距离为5 cm,则A,B两地间的实际距离为
12.如图中的两个三角形是否相似, 填“是”或“否”
13.《九章算术》中有一测井深的问题:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四尺,问井深几何?今译为:如图所示,有一口水井,井口直径为5尺,现竖立一根5尺长的木杆在井口,视线DC交井口AB于点E,BE的长为4尺,则水面距井口距离为 尺.
14.如图,将等边三角形ABC折叠,使得点C落在边AB上的点D处,折痕为EF,点E,F分别在边AC,BC上.如果,,那么的值为 .
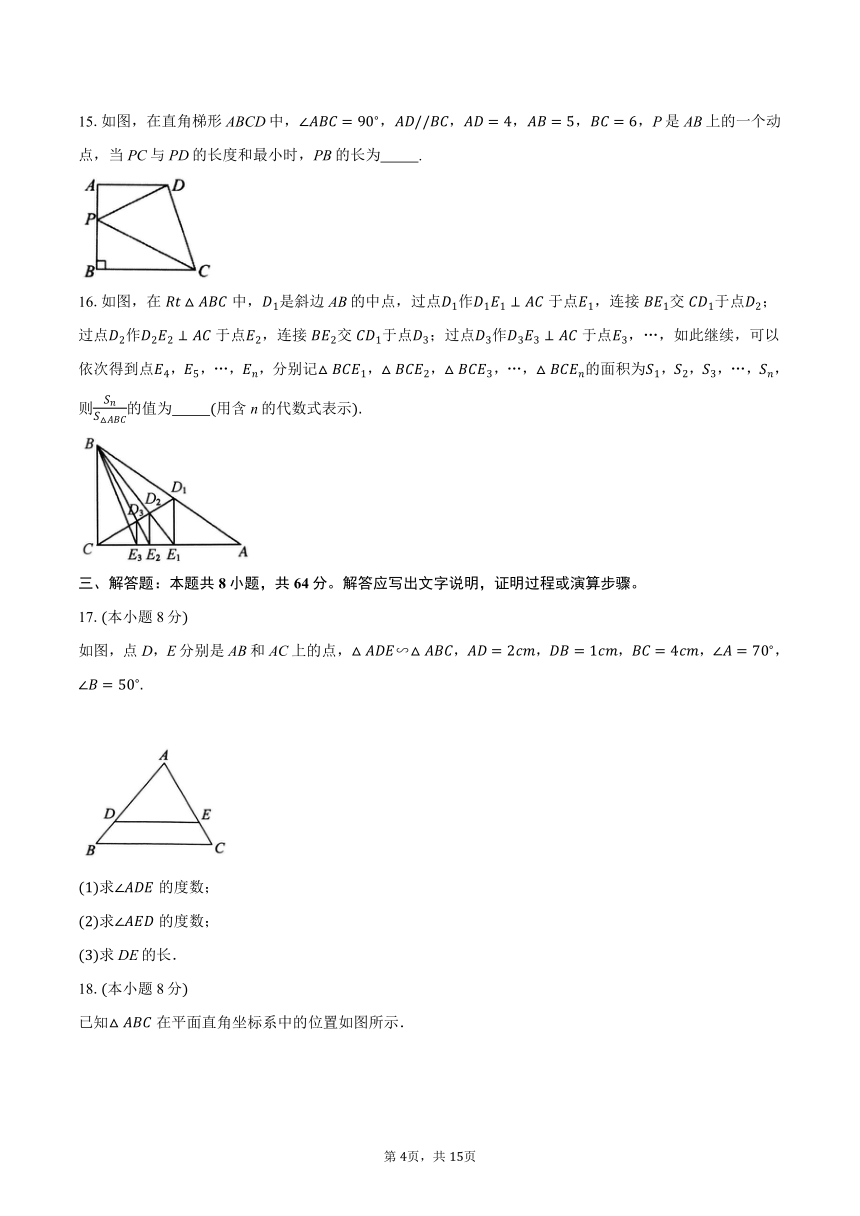
15.如图,在直角梯形ABCD中,,,,,,P是AB上的一个动点,当PC与PD的长度和最小时,PB的长为 .
16.如图,在中,是斜边AB的中点,过点作于点,连接交于点;过点作于点,连接交于点;过点作于点,…,如此继续,可以依次得到点,,…,,分别记,,,…,的面积为,,,…,,则的值为 用含n的代数式表示
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.本小题8分
如图,点D,E分别是AB和AC上的点,∽,,,,,
求的度数;
求的度数;
求DE的长.
18.本小题8分
已知在平面直角坐标系中的位置如图所示.
在图中画出沿x轴翻折后的;
以点为位似中心,作出按放大后的位似图形;
填空:点的坐标 ;与的周长比是 .
19.本小题8分
小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测倾器DC,测得古树的顶端A的视角为;再在BD的延长线上确定一点G,使米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得米,小明眼睛与地面的距离米,测倾器的高度米.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,求这棵古树的高度小平面镜的大小忽略不计
20.本小题8分
如图,在中,,点D在边BC上,已知,边DF交AC于点
求证:;
连接AD,如果,求证:
21.本小题8分
如图,以的直角边AB为直径作,交斜边AC于点D,E为OB的中点,连接CE并延长交于点F,点F恰好落在的中点,连接AF并延长与CB的延长线相交于点G,连接
求证:;
若,求DC的长.
22.本小题8分
如图,矩形ABCD中,,点P在AD上运动点P不与点A、D重合将沿直线翻折,使得点A落在矩形内的点M处包括矩形边界
求AP的取值范围;
连接DM并延长交矩形ABCD的AB边于点G,当时,求AP的长.
23.本小题8分
已知,的顶点A在ON上,顶点B在OM上,且,连接OC,与AB交于点
如图1,若,求证:OC平分;
如图2,若CA与ON不垂直,OC是否仍平分?请给出结论,并说明理由;
如图3,若,,求AD的长.
24.本小题8分
如图,在矩形ABCD中,BE平分交AD于点E,连接CE,F在BC边上,且,过点C作EF的垂线交BE于点G,垂足为点H,连接
若,求的度数;
求证:;
若F为BC的中点,求的值.
答案和解析
1.【答案】B
【解析】略
2.【答案】B
【解析】解:A、,成比例线段,故本选项不符合题意;
B、,不是成比例线段,故本选项符合题意;
C、,成比例线段,故本选项不符合题意;
D、,成比例线段,故本选项不符合题意.
故选:
只要判断四个数中最大的和最小的两个数的乘积等于中间两个数的乘积即可判断.
本题考查了比例线段,理解判断的方法:最大的和最小的两个数的乘积等于中间两个数的乘积是关键.
3.【答案】D
【解析】略
4.【答案】D
【解析】略
5.【答案】B
【解析】略
6.【答案】D
【解析】略
7.【答案】C
【解析】略
8.【答案】B
【解析】略
9.【答案】B
【解析】略
10.【答案】D
【解析】由四边形ABCD、四边形BEFG是正方形,可得≌,即得,即可证明,可判断①正确;取AC的中点K,可得,即可得,从而∽,判断②正确;由,可得点A、O、C、D四点共圆,而,故,判断④正确;不能证明OB平分,即可得答案.
11.【答案】100
【解析】略
12.【答案】是
【解析】略
13.【答案】
【解析】井口直径为5尺,,竖立一根5尺长的木杆在井口,,∽,,,解得
14.【答案】
【解析】略
15.【答案】3
【解析】略
16.【答案】
【解析】提示:根据直角三角形的性质以及相似三角形的性质可知,,,因为在中,为其重心,所以,所以,,所以,所以根据图中的变化规律,易得,,,…,所以
17.【答案】【小题1】
解:∽,
【小题2】
,,∽,
【小题3】
∽,,,
【解析】 略
略
略
18.【答案】【小题1】
如图,为所作;
【小题2】
如图,为所作;
【小题3】
【解析】 略
略
沿x轴翻折后得到,≌按放大后的位似图形,与的相似比为,与的相似比为,与的周长比为
19.【答案】解:如图,过点C作于点H
则,
在中,
,
又
∽
,即
解得
经检验:是原方程的解
这棵古树的高AB为18m
【解析】本题考查了相似三角形的应用,过点C作于点H,则,,由等腰直角三角形的性质,得出,那么,再证明∽,根据相似三角形对应边成比例求出,进而求出AB即可.
20.【答案】【小题1】
证明:,,,∽
【小题2】
,,∽,∽,,即
【解析】 略
略
21.【答案】【小题1】
证明:是的中点, 又, 又, 又,是的中位线.
【小题2】
解:是OB的中点, 又,,≌, 在中, 如图,连接是的直径, 又,∽,即
【解析】 略
略
22.【答案】【小题1】
当M落在CD上时,AP的长度达到最大.四边形ABCD是矩形,,,沿直线BP翻折,,,, ,,,∽,,,,,的取值范围是
【小题2】
将沿直线翻折,使得点A落在矩形内的点M处,, 又,,∽, 设, 过M作于点H,如图.
将沿直线翻折,使得点A落在矩形内的点M处,,,,,,,,为的中位线, 在中,,, 解得,舍去,
【解析】 略
略
23.【答案】【小题1】
证明:,,,四边形ACBO是矩形.又,矩形ACBO是正方形.平分;
【小题2】
解:OC平分,理由如下:过点C作于F,于E,则又,四边形ECFO是矩形.又,,≌又,,平分;
【小题3】
解:过点C作于H,由知,OC平分,在中,,又,∽,解得在中,,,
【解析】 略
略
略
24.【答案】【小题1】
,,, 在矩形ABCD中,平分, 在中,;
【小题2】
过点E作于点T,过点G作于点
,四边形ABTE是矩形.,四边形ABTE是正方形,,,,,,,,,,,,, 易证≌,,四边形DETC是矩形,是等腰直角三角形,
【小题3】
由知,四边形EDCT是矩形,点F为BC的中点, 设,则,,,是等腰直角三角形,,,,, 由知,∽,,即,解得,,
【解析】 略
略
略
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.两个相似三角形的周长比是则其相似比是( )
A. B. C. D.
2.下列各组线段中,不是成比例线段的是( )
A. 3,6,2,4 B. 4,6,5,10
C. 1,,, D. 2,,,
3.如图,四边形ABCD∽四边形EFGH,,,,则等于
A. B. C. D.
4.如图,AB与CD相交于点O,添加一个条件,不能判断∽的是
A. B. C. D.
5.如图,在平面直角坐标系xOy中,以原点O为位似中心,把线段AB放大后得到线段若点,,,则点A的对应点C的坐标是
A. B. C. D.
6.击地传球是篮球运动中的一种传球方式,利用击地传球可以有效地躲避对手的拦截.传球选手从点A处将球传出,经地面点O处反弹后被接球选手在点C处接住,将球所经过的路径视为直线,此时若点A距地面的高度AB为,点C距地面的高度CD为1 m,传球选手与接球选手之间的距离BD为5 m,则OB的长度为
A. B. 2 m C. D. 3 m
7.如图,E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF,若,则等于
A. B. C. D.
8.如图,在中,,高,正方形EFGH的一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为
A. 10 B. 8 C. 16 D. 12
9.西周数学家商高总结了用“矩”如图①测量物高的方法:把“矩”的两边放置成如图②的位置,从“矩”的一端人眼望点E,使视线通过点C,记人站立的位置为点B,量出BG的长,即可算得物高令,,若,,,则y关于x的函数解析式为
A. B. C. D.
10.如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是
①;②∽;③OB平分;④
A. ①③ B. ①②③ C. ②③ D. ①②④
二、填空题:本题共6小题,每小题3分,共18分。
11.在比例尺为的地图上测得A,B两地间的图上距离为5 cm,则A,B两地间的实际距离为
12.如图中的两个三角形是否相似, 填“是”或“否”
13.《九章算术》中有一测井深的问题:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四尺,问井深几何?今译为:如图所示,有一口水井,井口直径为5尺,现竖立一根5尺长的木杆在井口,视线DC交井口AB于点E,BE的长为4尺,则水面距井口距离为 尺.
14.如图,将等边三角形ABC折叠,使得点C落在边AB上的点D处,折痕为EF,点E,F分别在边AC,BC上.如果,,那么的值为 .
15.如图,在直角梯形ABCD中,,,,,,P是AB上的一个动点,当PC与PD的长度和最小时,PB的长为 .
16.如图,在中,是斜边AB的中点,过点作于点,连接交于点;过点作于点,连接交于点;过点作于点,…,如此继续,可以依次得到点,,…,,分别记,,,…,的面积为,,,…,,则的值为 用含n的代数式表示
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.本小题8分
如图,点D,E分别是AB和AC上的点,∽,,,,,
求的度数;
求的度数;
求DE的长.
18.本小题8分
已知在平面直角坐标系中的位置如图所示.
在图中画出沿x轴翻折后的;
以点为位似中心,作出按放大后的位似图形;
填空:点的坐标 ;与的周长比是 .
19.本小题8分
小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测倾器DC,测得古树的顶端A的视角为;再在BD的延长线上确定一点G,使米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得米,小明眼睛与地面的距离米,测倾器的高度米.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,求这棵古树的高度小平面镜的大小忽略不计
20.本小题8分
如图,在中,,点D在边BC上,已知,边DF交AC于点
求证:;
连接AD,如果,求证:
21.本小题8分
如图,以的直角边AB为直径作,交斜边AC于点D,E为OB的中点,连接CE并延长交于点F,点F恰好落在的中点,连接AF并延长与CB的延长线相交于点G,连接
求证:;
若,求DC的长.
22.本小题8分
如图,矩形ABCD中,,点P在AD上运动点P不与点A、D重合将沿直线翻折,使得点A落在矩形内的点M处包括矩形边界
求AP的取值范围;
连接DM并延长交矩形ABCD的AB边于点G,当时,求AP的长.
23.本小题8分
已知,的顶点A在ON上,顶点B在OM上,且,连接OC,与AB交于点
如图1,若,求证:OC平分;
如图2,若CA与ON不垂直,OC是否仍平分?请给出结论,并说明理由;
如图3,若,,求AD的长.
24.本小题8分
如图,在矩形ABCD中,BE平分交AD于点E,连接CE,F在BC边上,且,过点C作EF的垂线交BE于点G,垂足为点H,连接
若,求的度数;
求证:;
若F为BC的中点,求的值.
答案和解析
1.【答案】B
【解析】略
2.【答案】B
【解析】解:A、,成比例线段,故本选项不符合题意;
B、,不是成比例线段,故本选项符合题意;
C、,成比例线段,故本选项不符合题意;
D、,成比例线段,故本选项不符合题意.
故选:
只要判断四个数中最大的和最小的两个数的乘积等于中间两个数的乘积即可判断.
本题考查了比例线段,理解判断的方法:最大的和最小的两个数的乘积等于中间两个数的乘积是关键.
3.【答案】D
【解析】略
4.【答案】D
【解析】略
5.【答案】B
【解析】略
6.【答案】D
【解析】略
7.【答案】C
【解析】略
8.【答案】B
【解析】略
9.【答案】B
【解析】略
10.【答案】D
【解析】由四边形ABCD、四边形BEFG是正方形,可得≌,即得,即可证明,可判断①正确;取AC的中点K,可得,即可得,从而∽,判断②正确;由,可得点A、O、C、D四点共圆,而,故,判断④正确;不能证明OB平分,即可得答案.
11.【答案】100
【解析】略
12.【答案】是
【解析】略
13.【答案】
【解析】井口直径为5尺,,竖立一根5尺长的木杆在井口,,∽,,,解得
14.【答案】
【解析】略
15.【答案】3
【解析】略
16.【答案】
【解析】提示:根据直角三角形的性质以及相似三角形的性质可知,,,因为在中,为其重心,所以,所以,,所以,所以根据图中的变化规律,易得,,,…,所以
17.【答案】【小题1】
解:∽,
【小题2】
,,∽,
【小题3】
∽,,,
【解析】 略
略
略
18.【答案】【小题1】
如图,为所作;
【小题2】
如图,为所作;
【小题3】
【解析】 略
略
沿x轴翻折后得到,≌按放大后的位似图形,与的相似比为,与的相似比为,与的周长比为
19.【答案】解:如图,过点C作于点H
则,
在中,
,
又
∽
,即
解得
经检验:是原方程的解
这棵古树的高AB为18m
【解析】本题考查了相似三角形的应用,过点C作于点H,则,,由等腰直角三角形的性质,得出,那么,再证明∽,根据相似三角形对应边成比例求出,进而求出AB即可.
20.【答案】【小题1】
证明:,,,∽
【小题2】
,,∽,∽,,即
【解析】 略
略
21.【答案】【小题1】
证明:是的中点, 又, 又, 又,是的中位线.
【小题2】
解:是OB的中点, 又,,≌, 在中, 如图,连接是的直径, 又,∽,即
【解析】 略
略
22.【答案】【小题1】
当M落在CD上时,AP的长度达到最大.四边形ABCD是矩形,,,沿直线BP翻折,,,, ,,,∽,,,,,的取值范围是
【小题2】
将沿直线翻折,使得点A落在矩形内的点M处,, 又,,∽, 设, 过M作于点H,如图.
将沿直线翻折,使得点A落在矩形内的点M处,,,,,,,,为的中位线, 在中,,, 解得,舍去,
【解析】 略
略
23.【答案】【小题1】
证明:,,,四边形ACBO是矩形.又,矩形ACBO是正方形.平分;
【小题2】
解:OC平分,理由如下:过点C作于F,于E,则又,四边形ECFO是矩形.又,,≌又,,平分;
【小题3】
解:过点C作于H,由知,OC平分,在中,,又,∽,解得在中,,,
【解析】 略
略
略
24.【答案】【小题1】
,,, 在矩形ABCD中,平分, 在中,;
【小题2】
过点E作于点T,过点G作于点
,四边形ABTE是矩形.,四边形ABTE是正方形,,,,,,,,,,,,, 易证≌,,四边形DETC是矩形,是等腰直角三角形,
【小题3】
由知,四边形EDCT是矩形,点F为BC的中点, 设,则,,,是等腰直角三角形,,,,, 由知,∽,,即,解得,,
【解析】 略
略
略
第1页,共1页
