期中测试卷(含答案)---2024-2025学年五年级数学下册(北京版)
文档属性
| 名称 | 期中测试卷(含答案)---2024-2025学年五年级数学下册(北京版) |  | |
| 格式 | docx | ||
| 文件大小 | 103.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-05 13:02:22 | ||
图片预览




文档简介
保密★启用前
2024-2025学年五年级下册期中测试卷(北京版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.把一个棱长为1分米的正方体切割成棱长是1厘米的小正方体,然后将这些切割而成的小正方体排成一行,长( )厘米。
A.10 B.100 C.1000 D.10000
2.下面展开图中,不是正方体的展开图的是( )
A. B.
C. D.
3.下面四个数都是自然数,其中数字M不为0,下列各数中既是2的倍数,又是3的倍数的是( )。
A.M3M3 B.M0M0M0 C.M00M06 D.MM15
4.下列说法正确的是( )。
A.奇数×奇数=偶数
B.奇数+奇数=奇数
C.所有非0自然数中,不是质数就是合数
D.最小的合数是4
5.下列各组数中,都是质数的是( )。
A.1、3和7 B.2、5和29 C.39、49和57 D.11、17和21
6. 的分子加上8,如果要使这个分数的大小不变,分母应该( )。
A.加上30 B.加上8 C.扩大2倍 D.增加3倍
7.把5米的铁丝平均分成6段,每段占这根铁丝的 ( )。
A. 米 B.米 C. D.米
8.长方体的长、宽、高都扩大为原来的3倍,它的体积扩大为原来的( )。
A.3 B.9 C.27
9.求一个游泳池的占地面积实际是求它的 ( )。
A.侧面积 B.表面积 C.底面积
10.大于 2 的两个质数的积一定是 ( )。
A.质数 B.偶数 C.合数
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.1米的 和3米的 一样长。( )
12.一个正方体的棱长是6cm,它的表面积和体积相等。( )
13.自然数中,不是偶数就是奇数。( )
14.将一个正方体切成两个完全相同的长方体,每个长方体的表面积是这个正方体表面积的一半。( )
15.体积相等的两个长方体,表面积不一定相等。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.弟弟用3个棱长1厘米的小正方体拼成一个长方体,这个长方体的体积是 立方厘米,表面积是 平方厘米。
17.一个长方体容器从里面量,长是8dm,宽是5dm,高6dm,里面装有水,水面高4.5dm,现装有水 升。如果把体积为16dm3的石块浸没水中,这时水面上升 dm.
18.若一个正方体的棱长扩大3倍,则棱长总和扩大 倍,表面积扩大 倍,体积扩大 倍。
19.有两个质数,已知它们的和是18,积是65,这两个质数分别是 和 。
20.一枚一元硬币,正面朝上,翻动1次反面朝上,翻动2次正面朝上,以此类推,如果翻动100次,那么硬币的 面朝上。
21.三个连续偶数的和是48,那么这三个偶数中最大的是 。
22.把一根5米长的木条平均分成8段,每段长度是全长的 ,每段长 米。
23.下面阴影部分占整个图形的 ;分数单位是 ,再添上 个相同的分数单位就是最小的质数。
24.一堆砖堆成一个长方体,它的长是 10m,宽是 5.5m,高是 2m,这堆砖的占地面积是 。
25. 在括号里填上合适的单位。
①一间教室占地面积约是 60 ; ② 一盒牛奶约有 250 ;
③一块橡皮的体积约是 3 ;④一个集装箱的体积约是 40
阅卷人 四、计算题(23分)
得分
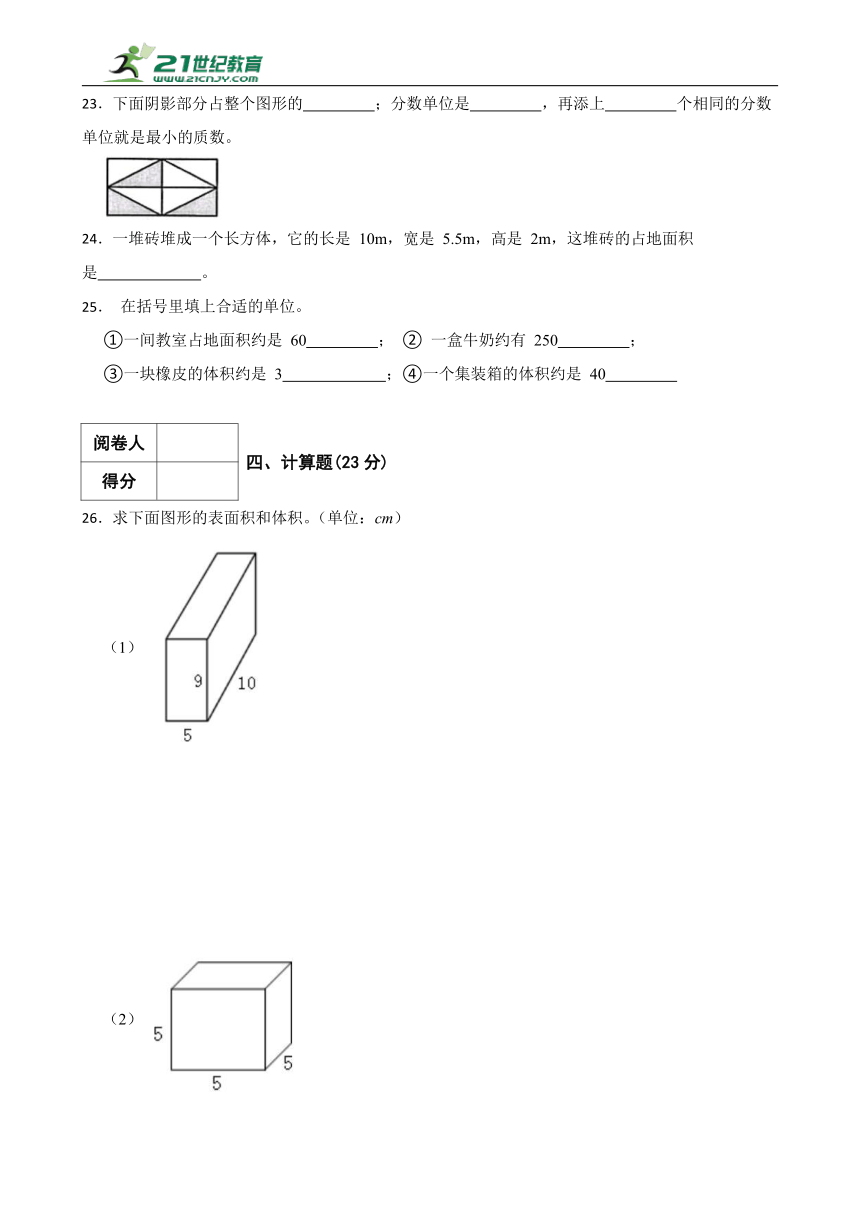
26.求下面图形的表面积和体积。(单位:cm)
(1)
(2)
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
27.明明和家人在周末参加了社区组织的“关爱空巢老人”志愿者活动,参加人数在50至80人之间,把这些志愿者按4人一组或6人一组都能正好分完,参加这次志愿者活动的人数至少有多少人?最多有多少人?
28.小林在自主学习时,用一根铁丝刚好围成一个长4dm、宽3dm、高2dm的长方体框架,之后他又用这根铁丝围成一个最大的正方体框架(且没有剩余)。正方体框架的棱长是多少dm
29.落实双减政策,某学校为了开设游泳课新建了一个游泳馆,长25米,宽11米,深2米。需要在游泳池的四周和底面铺上一层瓷砖,请问铺瓷砖的面积有多少平方米?
30.某小学六(2)班的学生分组进行植树活动,如果按8人一组,正好分完,如果按12人一组,也正好分完。这个班最少有多少名学生?
31.丹丹的房间长4m,宽3.5m,高2.8m,门窗面积是4m2,现在要粉刷这个房间的四壁和天花板。粉刷的面积是多少平方米?如果每平方米需要涂料0.3kg,一共需要多少千克涂料?
32.绿源小学的网络教室长15米、宽8米、高3米。在教室的四周贴上1.2米高的瓷砖,其中不用贴瓷砖的门窗面积是3.2平方米。
(1)贴瓷砖的面积有多大?
(2)如果每平方米瓷砖需要40元,每平方米贴瓷砖的人工费为15元,那么绿源小学的网络教室贴瓷砖一共需要多少元钱?
答案解析部分
1.C
解:1分米=10厘米
10×10×10×1
=100×10×1
=1000(厘米)。
故答案为:C。
1分米=10厘米,可以切割小正方体的个数=10×10×10=1000个,排成一行的长度=平均每个小正方体的棱长×个数。
2.D
解:不是正方体的展开图。
故答案为:D。
前三项分别是正方体展开图的“1-4-1”型、“2-2-2”型、“3-3”型;第四项不是正方体的展开图。
3.B
解:M0M0M0里面有3个M,3和0,则M0M0M0既是3的倍数,也是2的倍数。
故答案为:B。
个位上是0、2、4、6、8的数是2的倍数; 一个数各个数位上的数的和是3的倍数,这个数就是3的倍数。
4.D
解:A项:奇数×奇数=奇数,原题干说法错误;
B项:奇数+奇数=奇数,原题干说法错误;
C项:1既不是质数也不是合数,原题干说法错误;
D项:最小的合数是4,原题干说法正确。
故答案为:D。
奇数×奇数=奇数,奇数+奇数=奇数,偶数+偶数=偶数,偶数×偶数=偶数,1既不是质数也不是合数,最小的偶数是4,最小的质数是2。
5.B
A选项中“1”不是质数;B选项中都是质数;C选项中“49”不是质数;D选项中“21”不是质数。
故答案为:B
只有1和它本身两个因数的数,叫做质数;除了1和它本身以外还有其他因数的数叫做合数。据此判断即可。
6.A
(8+4)÷4=3,
15×3-15=30.
故答案为:A.
先计算出分子扩大的倍数,则分母应扩大相同的倍数,再减去原分母即可得到分母增加的多少.
7.C
解:1÷6=
故答案为:C。
根据题意可知,把铁丝的总长看作单位“1”,单位“1”÷平均分的段数=每段占这根铁丝的几分之几,据此列式解答。
8.C
解:3×3×3=27
故答案为:C。
长方体的体积=长×宽×高,长方体的长、宽、高都扩大为原来的a倍,它的体积扩大为原来的a3倍,据此列式解答。
9.C
解:求一个游泳池的占地面积实际是求它的底面积。
故答案为:C。
此题主要考查了立体图形表面积的认识,求一个游泳池的占地面积实际是求它的底面积。
10.C
解:大于 2 的两个质数的积一定是合数。
故答案为:C。
因为质数是只有1和它本身两个因数的数,两个质数的积至少会有3个因数:1和它本身;还有两个质数的乘积,所以说两个质数的积一定是合数。
11.正确
1米的 是 :1×=(米)
3米的 是:3×=(米)
故答案为:正确
“求一个数的几分之几是多少”用乘法。
12.错误
表面积和体积不能进行比较,原题说法错误。
故答案为:错误。
表面积是面积单位,体积是体积单位,单位不一样,无法比较大小。
13.正确
解:自然数中,不是偶数就是奇数,原题干说法正确。
故答案为:正确。
自然数按照是否是2的倍数,可以分为奇数和偶数。
14.错误
解:每个长方体的表面积不是这个正方体表面积的一半。原题错误。
故答案为:错误。
2个长方体的表面积之和比正方体的表面积多了2个面的面积。
15.正确
解:体积相等的两个长方体,表面积不一定相等。原题说法正确。
故答案为:正确。
体积相等的两个长方体,说明长宽高的乘积相等,但是不能保证表面积是相等的。
16.3;14
解:3×1=3(厘米)
3×1×1=3(立方厘米)
(3×1+3×1+1×1)×2
=7×2
=14(平方厘米)。
故答案为:3;14。
长方体的体积=长×宽×高;长方体的表面积=(长×宽+长×高+宽×高)×2,其中,长=小正方体的棱长×3,宽=高=小正方体的棱长。
17.180;0.4
解:8×5×4.5
=40×4.5
=180(立方分米)
180立方分米=180升
16÷(8×5)
=16÷40
=0.4(分米)。
故答案为:180;0.4。
先装有水的体积=长方体容器的长×宽×水面的高度;这时水面上升的高度=石块的体积÷容器的底面积。
18.3;9;27
解:1×3=3
3×3=9
3×3×3=27。
故答案为:3;9;27。
正方体的棱长和=棱长×12;正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,若一个正方体的棱长扩大3倍,则棱长总和扩大3 倍,表面积扩大9倍,体积扩大27倍。
19.13;5
解:13+5=18
13×5=65。
故答案为:13;5。
依据100以内的质数表填空。
20.正
解:如果翻动100次,那么硬币的正面朝上。
故答案为:正。
一枚一元硬币,正面朝上,翻动1次反面朝上,翻动2次正面朝上,据此推测出翻动奇数次反面朝上,翻动偶数次正面朝上,100是偶数,则硬币的正面朝上。
21.18
解:48÷3=16
16-2=14
16+2=18,这三个偶数中最大的是18。
故答案为:18。
连续的偶数相差2,中间的一个偶数=三个连续偶数的和÷3,最大的一个偶数=中间的一个偶数+2。
22.;
解:1÷8=;
5÷8=(米)。
故答案为:;。
每段长度是全长的分率=1÷平均分的份数;每段的长度=木条的总长度÷平均分的份数。
23.;;13
解:3÷8=;分数单位是;
2-=,再添上13个相同的分数单位就是最小的质数。
故答案为:;;13。
阴影部分占整个图形的分率=阴影部分占的份数÷整个图形平均分的份数;
最小的质数是2,再添上分数单位的个数是2-=,再添上13个相同的分数单位就是最小的质数。
24.55平方米
解:10×5.5=55(平方米)
故答案为:55平方米。
长方体的占地面积=长×宽,据此列式解答。
25.平方米;毫升;立方厘米;立方米
解:①一间教室占地面积约是 60平方米; ② 一盒牛奶约有 250毫升;
③一块橡皮的体积约是 3立方厘米;④一个集装箱的体积约是 40立方米。
故答案为:平方米;毫升;立方厘米;立方米。
常见的面积单位的有公顷、平方米、平方分米、平方厘米,常见的体积单位有立方米、立方分米、立方厘米,容积单位有升、毫升,根据数据大小与生活实际,选择合适的单位。
26.(1)解:(10×5+10×9+5×9)×2
=(50+90+45)×2
=185×2
=370(平方厘米)
10×5×9
=50×9
=450(立方厘米)
答:长方体的表面积是370平方厘米,体积是450立方厘米。
(2)解:5×5×6
=25×6
=150(平方厘米)
5×5×5
=25×5
=125(立方厘米)
答:正方体的表面积是150平方厘米,体积是125立方厘米。
(1)长方体的体积=长×宽×高;长方体的表面积=(长×宽+长×高+宽×高)×2;
(2)正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。
27.解:4=2×2
6=2×3
4和6的最小公倍数是:2×2×3=12,
12×5=60(人)
12×6=72(人)
答:参加这次志愿者活动的人数至少有60人,最多有72人。
把这些志愿者按4人一组或6人一组都能正好分完,说明参加这次志愿者活动的人数是4和6的公倍数;
满足50至80之间,4和6的公倍数的数就是参加这次志愿者活动的人数。
28.解:(4+3+2)×4÷12
=9×4÷12
=36÷12
=3(dm)
答:正方体框架的棱长是3dm。
长方体棱长和=(长+宽+高)×4,正方体棱长和=棱长×12。所以先求出长方体的棱长和也就是铁丝的长度,用铁丝的长度除以12即可求出正方体的棱长。
29.解:25×11+(25×2+11×2)×2
=25×11+(50+22)×2
=25×11+72×2
=275+144
=419(平方米)
答:铺瓷砖的面积有419平方米。
铺瓷砖的面积是去掉上面后的五个面的面积,铺瓷砖的面积=长×宽+(长×高+宽×高)×2。
30.解:8=2×2×2
12=2×2×3
8和12的最小公倍数是2×2×2×3=24
答:这个班最少有24名学生。
8和12的最小公倍数就是这个班的最少人数。
31.解:4×3.5+(4×2.8+3.5×2.8)×2-4
=14+(11.2+9.8)×2-4
=14+21×2-4
=14+42-4
=56-4
=52(平方米)
52×0.3=15.6(千克)
答:粉刷的面积是50平方米; 如果每平方米需要涂料0.3kg,一共需要15.6千克涂料。
长方体的表面积=(长×宽+长×高+宽×高)×2,本题中粉刷的面积=长×宽+(长×高+宽×高)×2-门窗的面积;一共需要涂料的千克数=粉刷的面积×每平方米需要涂料的千克数,代入数值计算即可。
32.(1)解:15×1.2×2+8×1.2×2﹣3.2
=36+19.2-3.2
=52(平方米)
答:贴瓷砖的面积有52平方米。
(2)解:52×(40+15)
=52×55
=2860(元)
答:绿源小学的网络教室贴瓷砖一共需要2860元钱。
(1)教室长×瓷砖高×2+教室宽×瓷砖高×2-门窗面积=贴瓷砖的面积;
(2)每平方米瓷砖钱数+每平方米人工费=每平方米的费用,每平方米的费用×贴瓷砖的面积=一共需要的钱数。
2024-2025学年五年级下册期中测试卷(北京版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.把一个棱长为1分米的正方体切割成棱长是1厘米的小正方体,然后将这些切割而成的小正方体排成一行,长( )厘米。
A.10 B.100 C.1000 D.10000
2.下面展开图中,不是正方体的展开图的是( )
A. B.
C. D.
3.下面四个数都是自然数,其中数字M不为0,下列各数中既是2的倍数,又是3的倍数的是( )。
A.M3M3 B.M0M0M0 C.M00M06 D.MM15
4.下列说法正确的是( )。
A.奇数×奇数=偶数
B.奇数+奇数=奇数
C.所有非0自然数中,不是质数就是合数
D.最小的合数是4
5.下列各组数中,都是质数的是( )。
A.1、3和7 B.2、5和29 C.39、49和57 D.11、17和21
6. 的分子加上8,如果要使这个分数的大小不变,分母应该( )。
A.加上30 B.加上8 C.扩大2倍 D.增加3倍
7.把5米的铁丝平均分成6段,每段占这根铁丝的 ( )。
A. 米 B.米 C. D.米
8.长方体的长、宽、高都扩大为原来的3倍,它的体积扩大为原来的( )。
A.3 B.9 C.27
9.求一个游泳池的占地面积实际是求它的 ( )。
A.侧面积 B.表面积 C.底面积
10.大于 2 的两个质数的积一定是 ( )。
A.质数 B.偶数 C.合数
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.1米的 和3米的 一样长。( )
12.一个正方体的棱长是6cm,它的表面积和体积相等。( )
13.自然数中,不是偶数就是奇数。( )
14.将一个正方体切成两个完全相同的长方体,每个长方体的表面积是这个正方体表面积的一半。( )
15.体积相等的两个长方体,表面积不一定相等。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.弟弟用3个棱长1厘米的小正方体拼成一个长方体,这个长方体的体积是 立方厘米,表面积是 平方厘米。
17.一个长方体容器从里面量,长是8dm,宽是5dm,高6dm,里面装有水,水面高4.5dm,现装有水 升。如果把体积为16dm3的石块浸没水中,这时水面上升 dm.
18.若一个正方体的棱长扩大3倍,则棱长总和扩大 倍,表面积扩大 倍,体积扩大 倍。
19.有两个质数,已知它们的和是18,积是65,这两个质数分别是 和 。
20.一枚一元硬币,正面朝上,翻动1次反面朝上,翻动2次正面朝上,以此类推,如果翻动100次,那么硬币的 面朝上。
21.三个连续偶数的和是48,那么这三个偶数中最大的是 。
22.把一根5米长的木条平均分成8段,每段长度是全长的 ,每段长 米。
23.下面阴影部分占整个图形的 ;分数单位是 ,再添上 个相同的分数单位就是最小的质数。
24.一堆砖堆成一个长方体,它的长是 10m,宽是 5.5m,高是 2m,这堆砖的占地面积是 。
25. 在括号里填上合适的单位。
①一间教室占地面积约是 60 ; ② 一盒牛奶约有 250 ;
③一块橡皮的体积约是 3 ;④一个集装箱的体积约是 40
阅卷人 四、计算题(23分)
得分
26.求下面图形的表面积和体积。(单位:cm)
(1)
(2)
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
27.明明和家人在周末参加了社区组织的“关爱空巢老人”志愿者活动,参加人数在50至80人之间,把这些志愿者按4人一组或6人一组都能正好分完,参加这次志愿者活动的人数至少有多少人?最多有多少人?
28.小林在自主学习时,用一根铁丝刚好围成一个长4dm、宽3dm、高2dm的长方体框架,之后他又用这根铁丝围成一个最大的正方体框架(且没有剩余)。正方体框架的棱长是多少dm
29.落实双减政策,某学校为了开设游泳课新建了一个游泳馆,长25米,宽11米,深2米。需要在游泳池的四周和底面铺上一层瓷砖,请问铺瓷砖的面积有多少平方米?
30.某小学六(2)班的学生分组进行植树活动,如果按8人一组,正好分完,如果按12人一组,也正好分完。这个班最少有多少名学生?
31.丹丹的房间长4m,宽3.5m,高2.8m,门窗面积是4m2,现在要粉刷这个房间的四壁和天花板。粉刷的面积是多少平方米?如果每平方米需要涂料0.3kg,一共需要多少千克涂料?
32.绿源小学的网络教室长15米、宽8米、高3米。在教室的四周贴上1.2米高的瓷砖,其中不用贴瓷砖的门窗面积是3.2平方米。
(1)贴瓷砖的面积有多大?
(2)如果每平方米瓷砖需要40元,每平方米贴瓷砖的人工费为15元,那么绿源小学的网络教室贴瓷砖一共需要多少元钱?
答案解析部分
1.C
解:1分米=10厘米
10×10×10×1
=100×10×1
=1000(厘米)。
故答案为:C。
1分米=10厘米,可以切割小正方体的个数=10×10×10=1000个,排成一行的长度=平均每个小正方体的棱长×个数。
2.D
解:不是正方体的展开图。
故答案为:D。
前三项分别是正方体展开图的“1-4-1”型、“2-2-2”型、“3-3”型;第四项不是正方体的展开图。
3.B
解:M0M0M0里面有3个M,3和0,则M0M0M0既是3的倍数,也是2的倍数。
故答案为:B。
个位上是0、2、4、6、8的数是2的倍数; 一个数各个数位上的数的和是3的倍数,这个数就是3的倍数。
4.D
解:A项:奇数×奇数=奇数,原题干说法错误;
B项:奇数+奇数=奇数,原题干说法错误;
C项:1既不是质数也不是合数,原题干说法错误;
D项:最小的合数是4,原题干说法正确。
故答案为:D。
奇数×奇数=奇数,奇数+奇数=奇数,偶数+偶数=偶数,偶数×偶数=偶数,1既不是质数也不是合数,最小的偶数是4,最小的质数是2。
5.B
A选项中“1”不是质数;B选项中都是质数;C选项中“49”不是质数;D选项中“21”不是质数。
故答案为:B
只有1和它本身两个因数的数,叫做质数;除了1和它本身以外还有其他因数的数叫做合数。据此判断即可。
6.A
(8+4)÷4=3,
15×3-15=30.
故答案为:A.
先计算出分子扩大的倍数,则分母应扩大相同的倍数,再减去原分母即可得到分母增加的多少.
7.C
解:1÷6=
故答案为:C。
根据题意可知,把铁丝的总长看作单位“1”,单位“1”÷平均分的段数=每段占这根铁丝的几分之几,据此列式解答。
8.C
解:3×3×3=27
故答案为:C。
长方体的体积=长×宽×高,长方体的长、宽、高都扩大为原来的a倍,它的体积扩大为原来的a3倍,据此列式解答。
9.C
解:求一个游泳池的占地面积实际是求它的底面积。
故答案为:C。
此题主要考查了立体图形表面积的认识,求一个游泳池的占地面积实际是求它的底面积。
10.C
解:大于 2 的两个质数的积一定是合数。
故答案为:C。
因为质数是只有1和它本身两个因数的数,两个质数的积至少会有3个因数:1和它本身;还有两个质数的乘积,所以说两个质数的积一定是合数。
11.正确
1米的 是 :1×=(米)
3米的 是:3×=(米)
故答案为:正确
“求一个数的几分之几是多少”用乘法。
12.错误
表面积和体积不能进行比较,原题说法错误。
故答案为:错误。
表面积是面积单位,体积是体积单位,单位不一样,无法比较大小。
13.正确
解:自然数中,不是偶数就是奇数,原题干说法正确。
故答案为:正确。
自然数按照是否是2的倍数,可以分为奇数和偶数。
14.错误
解:每个长方体的表面积不是这个正方体表面积的一半。原题错误。
故答案为:错误。
2个长方体的表面积之和比正方体的表面积多了2个面的面积。
15.正确
解:体积相等的两个长方体,表面积不一定相等。原题说法正确。
故答案为:正确。
体积相等的两个长方体,说明长宽高的乘积相等,但是不能保证表面积是相等的。
16.3;14
解:3×1=3(厘米)
3×1×1=3(立方厘米)
(3×1+3×1+1×1)×2
=7×2
=14(平方厘米)。
故答案为:3;14。
长方体的体积=长×宽×高;长方体的表面积=(长×宽+长×高+宽×高)×2,其中,长=小正方体的棱长×3,宽=高=小正方体的棱长。
17.180;0.4
解:8×5×4.5
=40×4.5
=180(立方分米)
180立方分米=180升
16÷(8×5)
=16÷40
=0.4(分米)。
故答案为:180;0.4。
先装有水的体积=长方体容器的长×宽×水面的高度;这时水面上升的高度=石块的体积÷容器的底面积。
18.3;9;27
解:1×3=3
3×3=9
3×3×3=27。
故答案为:3;9;27。
正方体的棱长和=棱长×12;正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,若一个正方体的棱长扩大3倍,则棱长总和扩大3 倍,表面积扩大9倍,体积扩大27倍。
19.13;5
解:13+5=18
13×5=65。
故答案为:13;5。
依据100以内的质数表填空。
20.正
解:如果翻动100次,那么硬币的正面朝上。
故答案为:正。
一枚一元硬币,正面朝上,翻动1次反面朝上,翻动2次正面朝上,据此推测出翻动奇数次反面朝上,翻动偶数次正面朝上,100是偶数,则硬币的正面朝上。
21.18
解:48÷3=16
16-2=14
16+2=18,这三个偶数中最大的是18。
故答案为:18。
连续的偶数相差2,中间的一个偶数=三个连续偶数的和÷3,最大的一个偶数=中间的一个偶数+2。
22.;
解:1÷8=;
5÷8=(米)。
故答案为:;。
每段长度是全长的分率=1÷平均分的份数;每段的长度=木条的总长度÷平均分的份数。
23.;;13
解:3÷8=;分数单位是;
2-=,再添上13个相同的分数单位就是最小的质数。
故答案为:;;13。
阴影部分占整个图形的分率=阴影部分占的份数÷整个图形平均分的份数;
最小的质数是2,再添上分数单位的个数是2-=,再添上13个相同的分数单位就是最小的质数。
24.55平方米
解:10×5.5=55(平方米)
故答案为:55平方米。
长方体的占地面积=长×宽,据此列式解答。
25.平方米;毫升;立方厘米;立方米
解:①一间教室占地面积约是 60平方米; ② 一盒牛奶约有 250毫升;
③一块橡皮的体积约是 3立方厘米;④一个集装箱的体积约是 40立方米。
故答案为:平方米;毫升;立方厘米;立方米。
常见的面积单位的有公顷、平方米、平方分米、平方厘米,常见的体积单位有立方米、立方分米、立方厘米,容积单位有升、毫升,根据数据大小与生活实际,选择合适的单位。
26.(1)解:(10×5+10×9+5×9)×2
=(50+90+45)×2
=185×2
=370(平方厘米)
10×5×9
=50×9
=450(立方厘米)
答:长方体的表面积是370平方厘米,体积是450立方厘米。
(2)解:5×5×6
=25×6
=150(平方厘米)
5×5×5
=25×5
=125(立方厘米)
答:正方体的表面积是150平方厘米,体积是125立方厘米。
(1)长方体的体积=长×宽×高;长方体的表面积=(长×宽+长×高+宽×高)×2;
(2)正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。
27.解:4=2×2
6=2×3
4和6的最小公倍数是:2×2×3=12,
12×5=60(人)
12×6=72(人)
答:参加这次志愿者活动的人数至少有60人,最多有72人。
把这些志愿者按4人一组或6人一组都能正好分完,说明参加这次志愿者活动的人数是4和6的公倍数;
满足50至80之间,4和6的公倍数的数就是参加这次志愿者活动的人数。
28.解:(4+3+2)×4÷12
=9×4÷12
=36÷12
=3(dm)
答:正方体框架的棱长是3dm。
长方体棱长和=(长+宽+高)×4,正方体棱长和=棱长×12。所以先求出长方体的棱长和也就是铁丝的长度,用铁丝的长度除以12即可求出正方体的棱长。
29.解:25×11+(25×2+11×2)×2
=25×11+(50+22)×2
=25×11+72×2
=275+144
=419(平方米)
答:铺瓷砖的面积有419平方米。
铺瓷砖的面积是去掉上面后的五个面的面积,铺瓷砖的面积=长×宽+(长×高+宽×高)×2。
30.解:8=2×2×2
12=2×2×3
8和12的最小公倍数是2×2×2×3=24
答:这个班最少有24名学生。
8和12的最小公倍数就是这个班的最少人数。
31.解:4×3.5+(4×2.8+3.5×2.8)×2-4
=14+(11.2+9.8)×2-4
=14+21×2-4
=14+42-4
=56-4
=52(平方米)
52×0.3=15.6(千克)
答:粉刷的面积是50平方米; 如果每平方米需要涂料0.3kg,一共需要15.6千克涂料。
长方体的表面积=(长×宽+长×高+宽×高)×2,本题中粉刷的面积=长×宽+(长×高+宽×高)×2-门窗的面积;一共需要涂料的千克数=粉刷的面积×每平方米需要涂料的千克数,代入数值计算即可。
32.(1)解:15×1.2×2+8×1.2×2﹣3.2
=36+19.2-3.2
=52(平方米)
答:贴瓷砖的面积有52平方米。
(2)解:52×(40+15)
=52×55
=2860(元)
答:绿源小学的网络教室贴瓷砖一共需要2860元钱。
(1)教室长×瓷砖高×2+教室宽×瓷砖高×2-门窗面积=贴瓷砖的面积;
(2)每平方米瓷砖钱数+每平方米人工费=每平方米的费用,每平方米的费用×贴瓷砖的面积=一共需要的钱数。
同课章节目录
