2024-2025学年浙教版七年级(下)数学期末模拟试题(含解析)
文档属性
| 名称 | 2024-2025学年浙教版七年级(下)数学期末模拟试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-05 00:00:00 | ||
图片预览




文档简介
2024-2025学年浙教版七年级(下)数学期末模拟试题
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.化简的结果是( )
A. B. C. D.
2.下列各组图形的变化中,属于平移的是( )
A. B.
C. D.
3.2022年6月5日10时44分07秒,神舟14号飞船成功发射,将陈冬、刘洋、蔡旭哲三位宇航员送入了中国空间站.已知中国空间站绕地球运行的速度约为,则中国空间站绕地球运行走过的路程(m)用科学记数法可表示为( )
A. B. C. D.
4.用代入法解方程组时,使得代入后化简比较简单的变形是( )
A.由①得 B.由①得
C.由②得 D.由②得
5.下列说法:
①是直线,若,则;
②夹在两条平行线间的线段的长度,叫作这两条平行线的距离;
③不相交的两条直线叫作平行线;
④经过直线外一点,有且只有一条直线与已知直线平行.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.下列方程中,是二元一次方程的是( )
A. B. C. D.
7.如图,已知两平行线、被直线所截,,则的度数为( )
A. B. C. D.
8.如图,直线a,b被直线c所截,其中一对同位角是( )
A.与 B.与
C.与 D.与
9.下列说法正确的是( )
A.过任意一点可作已知直线的一条平行线
B.两条不相交的直线是平行线
C.过直线上一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
10.如图是一款小推车的示意图,其中扶手平行于座板,前轮支撑杆平行于推杆,若,则的度数为( )
A. B. C. D.
11.如图,下列推理中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
12.桌面上有若干枚壹元硬币和伍角硬币,其中10枚正面向上.现将壹元硬币全部翻面,此时正面向上的壹元硬币比正面向上的伍角硬币多2枚,则桌面上的壹元硬币有( )
A.12枚 B.11枚 C.10枚 D.9枚
二、填空题
13.如图,取一张长方形的硬纸板,将硬纸板对折使与重合,为折痕.把长方形平放在桌面上,另一个面无论怎么改变位置,总有存在,理由是 .
14.已知 x,y 是方程组的解,则 x y 的值为 .
15.计算的结果是 .
16.一生态牧场上的草每天均匀生长.这片草可供16头牛吃60天,或者供18头牛吃50天.如果将这片草全部割下制成干草以备冬天的草料,但制成干草后使用要比直接使用青草损失的营养.那么,由这些割下来的草所制成的干草可供30头牛吃 天.
17.若,则的末位数字是 .
18.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,会发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,,则的度数为 .
三、解答题
19.解方程组:
(1);
(2).
20.计算:
(1);
(2)先化简,再求值:,其中,.
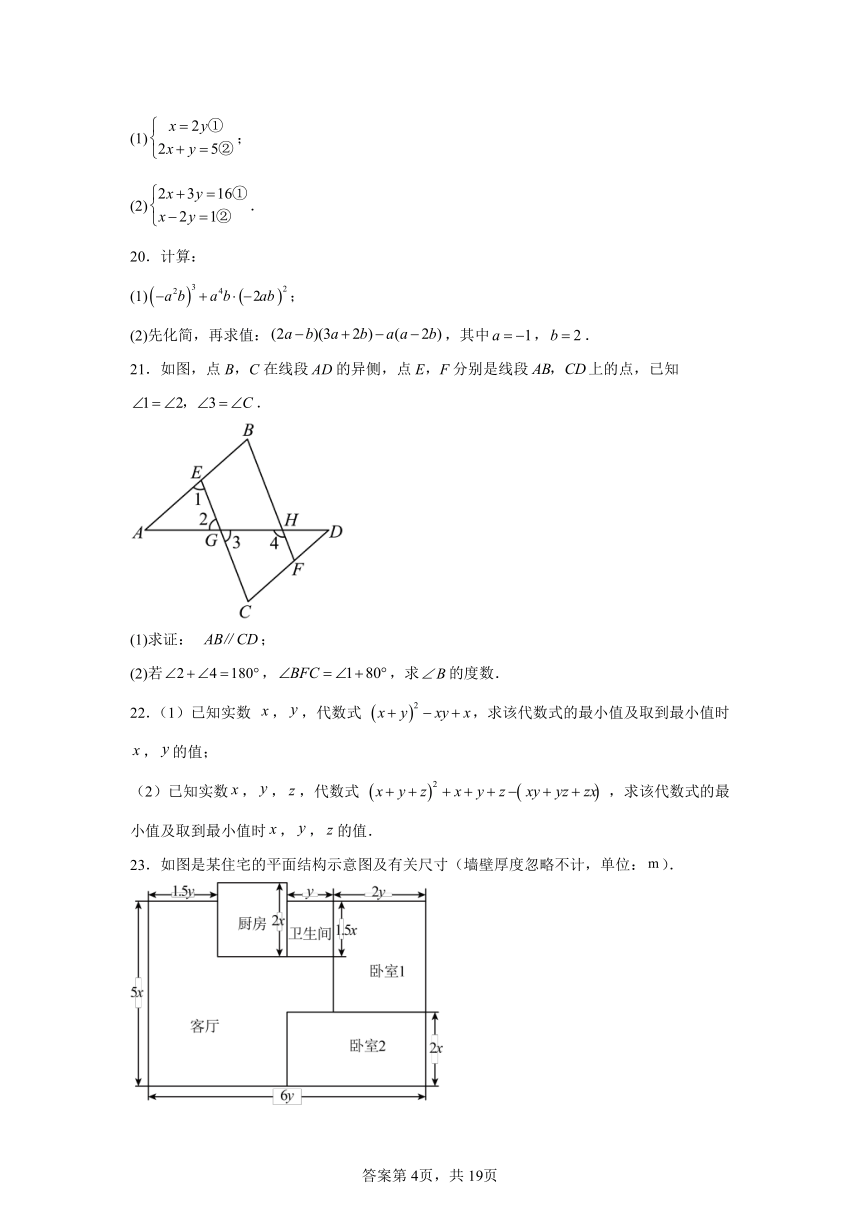
21.如图,点B,C在线段的异侧,点E,F分别是线段上的点,已知.
(1)求证: ;
(2)若,,求的度数.
22.(1)已知实数 ,,代数式 ,求该代数式的最小值及取到最小值时,的值;
(2)已知实数,,,代数式 ,求该代数式的最小值及取到最小值时,,的值.
23.如图是某住宅的平面结构示意图及有关尺寸(墙壁厚度忽略不计,单位:).
(1)求该住宅的面积(用含,的代数式表示).
(2)该住宅的主人计划把卧室以外的地面都铺上地砖,其中卫生间的地面面积为.如果地砖的价格是每平方米80元,那么购买地砖至少需要花费多少元?
24.已知:用辆型车和辆型车载满货物一次可运货吨;用辆型车和辆型车载满货物一次可运货吨.某物流公司现有吨货物,计划同时租用型车a辆,型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)辆型车和辆车型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若型车每辆需租金元次,型车每辆需租金元次.请选出最省钱的租车方案,并求出最少租车费.
25.阅读感悟:
有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x、y满足①,②,求和的值.
本题常规思路是将①②两式联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①②可得,由①②可得.这样的解题思想就是通常所说的“整体思想”.请根据上述思想解决下列问题:
(1)已知二元一次方程组,分别求和的值;
(2)对于实数x、y,定义新运算:,其中a、b、c是常数,等式右边是通常的加法和乘法运算.已知,求的值.
26.问题情境:如图1,,,,求度数.小明的思路是:过作,如图2,通过平行线性质来求.
(1)按小明的思路,易求得的度数为______;
问题迁移:
(2)如图3,,点在射线上运动,当点在、两点之间运动时,,,则、、之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请你判断、、间的数量关系并证明.
参考答案
1.【考点】同底数幂相乘
【分析】本题考查同底数幂的乘法,熟练掌握同底数幂的乘法法则是解题的关键.先利用乘方变为同底数幂的乘法,再计算即可.
解:
,
故选:D.
2.【考点】生活中的平移现象
【分析】本题考查平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.根据平移的性质,结合图形,选出正确答案.
解:各组图形中,选项A中的图形是一个图形经过平移能得到另一个图形,
故选:A.
3.【考点】同底数幂相乘、用科学记数法表示数的乘法
【分析】先求出路程,再用科学记数法表示为的形式.
解:路程=.
故选:B.
【点评】此题考查科学记数法的表示方法,表示时关键要正确确定a的值以及n的值.科学记数法的表示形式为的形式,其中1≤|a|<10,n为整数.
4.【考点】代入消元法
【分析】本题考查代入法解方程组,根据代入法,找到未知数的系数为的方程,将系数为的未知数用另一个未知数进行表示变形,判断即可.
解:观察可知:方程①中的系数为,
故变形比较简单的是由①得;
故选B.
5.【考点】平行公理的应用、求平行线间的距离
【分析】本题主要考查平行线的判定和性质,掌握平行线的判定方法和性质是解题的关键.
根据平行与同一条直线的两条直线相互平行可判定①;根据平行线间的垂线段处处相等可判定②;根据平行线的定义可判定③;根据平行线的基本事实可判定④;由此即可求解.
解:平行具有传递性,故①正确;
夹在两条平行线间的垂线段的长度,叫作这两条平行线的距离,故②错误;
在同一平面内,不相交的两条直线叫作平行线,故③错误;
经过直线外一点,有且只有一条直线与已知直线平行,这是平行线的基本事实,故④正确.
综上所述,①④正确,
故选:B.
6.【考点】二元一次方程的定义
【分析】本题考查了二元一次方程的定义,含有两个未知数且未知数的次数都为1的整式方程,据此进行逐项分析,即可作答.
解:A、的次数为2,不是二元一次方程,不符合题意;
B、是二元一次方程,符合题意;
C、的次数为2,不是二元一次方程,不符合题意;
D、含有三个未知数,不是二元一次方程,不符合题意;
故选:B
7.【考点】利用邻补角互补求角度、根据平行线的性质求角的度数
【分析】本题考查平行线的性质,利用邻补角求度数,根据平行线的性质,得到,再根据邻补角求出的度数即可.
解:∵,
∴,
∴;
故选B.
8.【考点】同位角、内错角、同旁内角
【分析】此题考查了同位角、内错角、同旁内角.两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角,据此作答即可.
解:与是同旁内角,不是同位角,选项A不符合题意;
与不是同位角,选项A不符合题意;
与是同位角,选项C符合题意;
与不是同位角,选项D不符合题意;
故选:C.
9.【考点】垂线的定义理解、平面内两直线的位置关系、平行公理的应用
【分析】本题主要考查平行线和垂线的定义及平行公理,熟练掌握公理、定理是解决本题的关键.
根据平行线和垂线的定义及平行公理进行判断.
解:A.过不在直线上一点可作已知直线的一条平行线,故选项错误;
B.同一平面内两条不相交的直线是平行线,故选项错误;
C.同一平面内过直线上一点只能画一条直线与已知直线垂直,故选项错误;
D.平行于同一直线的两直线平行,故选项正确;
故选D.
10.【考点】根据平行线的性质求角的度数
【分析】本题考查了平行线的性质,熟练掌握平行线的性质是解答本题的关键.先根据得,所以,再根据得,即可得解.
解:,
,
,
,
,
故选:C.
11.【考点】内错角相等两直线平行、同旁内角互补两直线平行、同位角相等两直线平行
【分析】本题主要考查了平行线的判定定理,熟练掌握平行线的判定定理是解题的关键;
根据平行线的判定定理逐项分析判断即可解答.
解:A、由只能推出,故错误,不符合题意;
B、由,只能推出,故错误,不符合题意;
C、,根据同旁内角互补,两直线平行,可以推出,故正确;
D、由,只能推出,故错误,不符合题意.
故选:C.
12.【考点】根据实际问题列二元一次方程组
【分析】本题考查了二元一次方程的应用,设桌面上的壹元硬币有枚,其中翻面前正面朝上的有枚,根据题意列出方程,理解题意,列出正确方程是解题的关键.
解:设桌面上的壹元硬币有枚,其中正面朝上的有枚,则正面向上的伍角硬币为枚,
由题可得,解得,
故选:A.
13.【考点】平行公理的应用
【分析】本题考查了平行公理推论,根据平行于同一条直线的两条直线平行即可求解,正确理解平行公理推论是解题的关键,
解:∵,,
∴,
理由:平行于同一条直线的两条直线平行,
故答案为:平行于同一条直线的两条直线平行.
14.【考点】加减消元法
【分析】用①-②可直接求解.
解:
①-②得:
x y=2
故答案为:2
【点评】本题考查的是解二元一次方程组——加减消元法,掌握加减消元的方法是关键.
15.【考点】有理数的乘方运算、幂的乘方的逆用、积的乘方的逆用
【分析】本题考查了幂的运算,解题的关键是熟练掌握相关运算法则.
先将化为,将化为,再根据积的乘方的逆运算进行计算即可.
解:
,
故答案为:.
16.【考点】三元一次方程组的应用
【分析】本题考查了三元一次方程组的应用.设这个生态牧场的原有草料a千克,每天生长b千克,每头牛每天可吃c千克草料,根据“这片草可供16头牛吃60天,或者供18头牛吃50天”,可列出关于a,b的三元一次方程组,解之可用含c的代数式表示出a,b的值,再将其代入中,即可求出结论.
解:设这个生态牧场的原有草料a千克,每天生长b千克,每头牛每天可吃c千克草料,
根据题意得:,
解得:,
∴(天),
∴这些割下来的草所制成的干草可供30头牛吃16天.
故答案为:16.
17.【考点】有理数的乘方运算、运用平方差公式进行运算
【分析】本题主要考查了平方差公式的应用,乘方的运算,熟练掌握平方差公式是解题关键.根据平方差公式,得出,从而得到的末位数字是,即可得到答案.
解:
,
的末位数是,
的末位数字是,即的末位数字是,
的末位数字是,
故答案为:.
18.【考点】平行线的性质在生活中的应用
【分析】本题考查了平行线的性质,根据两直线平行同位角相等得出,再由两直线平行同旁内角互补即可得出答案.
解:如图:
∵水中的两条光线平行,,
∴,
∵水面和杯底互相平行,
∴,
∵,
故答案为:.
19.【考点】代入消元法、加减消元法
【分析】本题主要考查了解二元一次方程组,熟练掌握解二元一次方程的消元思想是解题的关键.
(1)把①代入②得:,将y的值代入①即可求出x的值;
(2)可消去y求出x的值,将x的值代入①即可求出y的值.
解:(1)解:
把①代入②得:,
解得:,
把代入①得:,
∴原不等式组得解为.
(2)解:,
得:,
解得:,
把代入①得:,
∴,
∴原不等式组得解为.
20.【考点】积的乘方运算、计算单项式乘单项式、多项式乘多项式——化简求值、整式的混合运算
【分析】(1)先算乘方,再算乘法,后算加减,即可解答;
(2)利用多项式乘多项式,单项式乘多项式的法则进行计算,然后把,的值代入化简后的式子进行计算即可解答.
本题考查了整式的混合运算化简求值,准确熟练地进行计算是解题的关键.
解:(1)解:
;
(2)解:
,
当,时,
原式.
21.【考点】内错角相等两直线平行、根据平行线判定与性质求角度
【分析】本题主要考查了平行线的判定、平行线的性质,灵活运用平行线的判定定理和性质定理是解答本题的关键.
(1)由已知条件结合对顶角相等可得,然后根据内错角相等、两直线平行即可证明结论;
(2)先证明,再结合可得,进而证得,由平行线的性质可得,即,再结合求解即可解答.
(1)证明:∵,,,
∴,
∴.
(2)解:∵,,,
∴,
∵,
∴,
∴,
∴,,
∴①,
又∵②,
∴①②联立可得,
∴.
22.【考点】运用完全平方公式进行运算、通过对完全平方公式变形求值、拆项、添项、配方、待定系数法
【分析】本题主要考查了配方法求解代数式的最值问题,熟练掌握完全平方公式和平方的非负性是解题关键.
(1)将原式变形为,再利用平方的非负性即可求解;
(2)多次利用完全平方公式将原式变形,再利用平方的非负性即可求解.
解:(1)原式
,
当,时,
即,时,代数式有最小值为0;
(2)令,
则原式
,,
当时,代数式有最小值.
23.【考点】列代数式、整式加减的应用、多项式乘多项式与图形面积
【分析】本题考查了列代数式,整式加减的应用,有理数乘法的应用,理解题意并正确列式是解题关键.
(1)根据图形列式计算即可;
(2)先根据卫生间的面积求出,再计算出卧室以外的面积,乘以地砖的价格求解即可.
(1)解: 即该住宅的面积;
(2)解:由图形可知,卫生间的面积为,
卫生间的地面面积为,
,
,
卧室1的面积为,
卧室2的面积为,
卧室以外的面积为,
(元).
答:购买地砖至少需要花费4500元.
24.【考点】方案问题(二元一次方程组的应用)、二元一次方程的解
【分析】本题考查了二元一次方程组和二元一次方程的应用,根据题意,正确列出二元一次方程组及二元一次方程是解题的关键.
(1)设每辆型车、型车都载满货物一次可以分别运货吨、吨,根据题意,列出二元一次方程组即可求解;
(2)根据题意,列出二元一次方程,再根据都是正整数解答即可求解;
(3)分别求出每一种方案的费用即可求解;
解:(1)解:设每辆型车、型车都载满货物一次可以分别运货吨、吨,
依题意得,,
解得,
答:1辆型车载满货物一次可运3吨,1辆型车载满货物一次可运4吨;
(2)解:由(1)得,,
∴,
∵都是正整数,
∴或或,
∴有种租车方案:
方案一:型车10辆,型车1辆;
方案二:型车6辆,型车4辆;
方案三:型车2辆,型车7辆;
(3)解:∵型车每辆需租金100元/次,型车每辆需租金120元/次,
∴方案一需租金:元;
方案二需租金:元;
方案三需租金:元;
∵,
∴最省钱的租车方案是方案三,
答:租型车2辆,型车7辆,最少租车费为1040元.
25.【考点】加减消元法、三元一次方程组的应用
【分析】本题考查了二元一次方程组的应用,三元一次方程组的应用,掌握整体思想解决问题是解题的关键.
(1)将两方程相加可求的值,将两方程相减可求的值;
(2)由题意列出方程组,再计算出①②的结果,即可求解.
解:(1)解:,
①②可得:,
①②可得:;
(2)解:∵,
∴,
①②可得:.
26.【考点】平行公理的应用、根据平行线的性质探究角的关系
【分析】本题考查了平行线的性质和判定的应用,熟悉平行线的性质,作出合适的辅助线是解决问题的关键.
(1)过作,通过平行线性质求即可;
(2)过作交于,推出,根据平行线的性质得出,,即可得出答案;
(3)画出图形,根据平行线的性质得出,,即可得出答案.
解:(1)过点作,如图2所示,
,
,
,,
,,
,,
.
(2),
理由是:如图3,过作交于,
,
,
,,
;
(3)当在延长线时,如图所示,
,
,,
.
当在延长线时,如图所示,
,
,,
.
答案第2页,共2页
答案第1页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.化简的结果是( )
A. B. C. D.
2.下列各组图形的变化中,属于平移的是( )
A. B.
C. D.
3.2022年6月5日10时44分07秒,神舟14号飞船成功发射,将陈冬、刘洋、蔡旭哲三位宇航员送入了中国空间站.已知中国空间站绕地球运行的速度约为,则中国空间站绕地球运行走过的路程(m)用科学记数法可表示为( )
A. B. C. D.
4.用代入法解方程组时,使得代入后化简比较简单的变形是( )
A.由①得 B.由①得
C.由②得 D.由②得
5.下列说法:
①是直线,若,则;
②夹在两条平行线间的线段的长度,叫作这两条平行线的距离;
③不相交的两条直线叫作平行线;
④经过直线外一点,有且只有一条直线与已知直线平行.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.下列方程中,是二元一次方程的是( )
A. B. C. D.
7.如图,已知两平行线、被直线所截,,则的度数为( )
A. B. C. D.
8.如图,直线a,b被直线c所截,其中一对同位角是( )
A.与 B.与
C.与 D.与
9.下列说法正确的是( )
A.过任意一点可作已知直线的一条平行线
B.两条不相交的直线是平行线
C.过直线上一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
10.如图是一款小推车的示意图,其中扶手平行于座板,前轮支撑杆平行于推杆,若,则的度数为( )
A. B. C. D.
11.如图,下列推理中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
12.桌面上有若干枚壹元硬币和伍角硬币,其中10枚正面向上.现将壹元硬币全部翻面,此时正面向上的壹元硬币比正面向上的伍角硬币多2枚,则桌面上的壹元硬币有( )
A.12枚 B.11枚 C.10枚 D.9枚
二、填空题
13.如图,取一张长方形的硬纸板,将硬纸板对折使与重合,为折痕.把长方形平放在桌面上,另一个面无论怎么改变位置,总有存在,理由是 .
14.已知 x,y 是方程组的解,则 x y 的值为 .
15.计算的结果是 .
16.一生态牧场上的草每天均匀生长.这片草可供16头牛吃60天,或者供18头牛吃50天.如果将这片草全部割下制成干草以备冬天的草料,但制成干草后使用要比直接使用青草损失的营养.那么,由这些割下来的草所制成的干草可供30头牛吃 天.
17.若,则的末位数字是 .
18.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,会发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,,则的度数为 .
三、解答题
19.解方程组:
(1);
(2).
20.计算:
(1);
(2)先化简,再求值:,其中,.
21.如图,点B,C在线段的异侧,点E,F分别是线段上的点,已知.
(1)求证: ;
(2)若,,求的度数.
22.(1)已知实数 ,,代数式 ,求该代数式的最小值及取到最小值时,的值;
(2)已知实数,,,代数式 ,求该代数式的最小值及取到最小值时,,的值.
23.如图是某住宅的平面结构示意图及有关尺寸(墙壁厚度忽略不计,单位:).
(1)求该住宅的面积(用含,的代数式表示).
(2)该住宅的主人计划把卧室以外的地面都铺上地砖,其中卫生间的地面面积为.如果地砖的价格是每平方米80元,那么购买地砖至少需要花费多少元?
24.已知:用辆型车和辆型车载满货物一次可运货吨;用辆型车和辆型车载满货物一次可运货吨.某物流公司现有吨货物,计划同时租用型车a辆,型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)辆型车和辆车型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若型车每辆需租金元次,型车每辆需租金元次.请选出最省钱的租车方案,并求出最少租车费.
25.阅读感悟:
有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x、y满足①,②,求和的值.
本题常规思路是将①②两式联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①②可得,由①②可得.这样的解题思想就是通常所说的“整体思想”.请根据上述思想解决下列问题:
(1)已知二元一次方程组,分别求和的值;
(2)对于实数x、y,定义新运算:,其中a、b、c是常数,等式右边是通常的加法和乘法运算.已知,求的值.
26.问题情境:如图1,,,,求度数.小明的思路是:过作,如图2,通过平行线性质来求.
(1)按小明的思路,易求得的度数为______;
问题迁移:
(2)如图3,,点在射线上运动,当点在、两点之间运动时,,,则、、之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请你判断、、间的数量关系并证明.
参考答案
1.【考点】同底数幂相乘
【分析】本题考查同底数幂的乘法,熟练掌握同底数幂的乘法法则是解题的关键.先利用乘方变为同底数幂的乘法,再计算即可.
解:
,
故选:D.
2.【考点】生活中的平移现象
【分析】本题考查平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.根据平移的性质,结合图形,选出正确答案.
解:各组图形中,选项A中的图形是一个图形经过平移能得到另一个图形,
故选:A.
3.【考点】同底数幂相乘、用科学记数法表示数的乘法
【分析】先求出路程,再用科学记数法表示为的形式.
解:路程=.
故选:B.
【点评】此题考查科学记数法的表示方法,表示时关键要正确确定a的值以及n的值.科学记数法的表示形式为的形式,其中1≤|a|<10,n为整数.
4.【考点】代入消元法
【分析】本题考查代入法解方程组,根据代入法,找到未知数的系数为的方程,将系数为的未知数用另一个未知数进行表示变形,判断即可.
解:观察可知:方程①中的系数为,
故变形比较简单的是由①得;
故选B.
5.【考点】平行公理的应用、求平行线间的距离
【分析】本题主要考查平行线的判定和性质,掌握平行线的判定方法和性质是解题的关键.
根据平行与同一条直线的两条直线相互平行可判定①;根据平行线间的垂线段处处相等可判定②;根据平行线的定义可判定③;根据平行线的基本事实可判定④;由此即可求解.
解:平行具有传递性,故①正确;
夹在两条平行线间的垂线段的长度,叫作这两条平行线的距离,故②错误;
在同一平面内,不相交的两条直线叫作平行线,故③错误;
经过直线外一点,有且只有一条直线与已知直线平行,这是平行线的基本事实,故④正确.
综上所述,①④正确,
故选:B.
6.【考点】二元一次方程的定义
【分析】本题考查了二元一次方程的定义,含有两个未知数且未知数的次数都为1的整式方程,据此进行逐项分析,即可作答.
解:A、的次数为2,不是二元一次方程,不符合题意;
B、是二元一次方程,符合题意;
C、的次数为2,不是二元一次方程,不符合题意;
D、含有三个未知数,不是二元一次方程,不符合题意;
故选:B
7.【考点】利用邻补角互补求角度、根据平行线的性质求角的度数
【分析】本题考查平行线的性质,利用邻补角求度数,根据平行线的性质,得到,再根据邻补角求出的度数即可.
解:∵,
∴,
∴;
故选B.
8.【考点】同位角、内错角、同旁内角
【分析】此题考查了同位角、内错角、同旁内角.两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角,据此作答即可.
解:与是同旁内角,不是同位角,选项A不符合题意;
与不是同位角,选项A不符合题意;
与是同位角,选项C符合题意;
与不是同位角,选项D不符合题意;
故选:C.
9.【考点】垂线的定义理解、平面内两直线的位置关系、平行公理的应用
【分析】本题主要考查平行线和垂线的定义及平行公理,熟练掌握公理、定理是解决本题的关键.
根据平行线和垂线的定义及平行公理进行判断.
解:A.过不在直线上一点可作已知直线的一条平行线,故选项错误;
B.同一平面内两条不相交的直线是平行线,故选项错误;
C.同一平面内过直线上一点只能画一条直线与已知直线垂直,故选项错误;
D.平行于同一直线的两直线平行,故选项正确;
故选D.
10.【考点】根据平行线的性质求角的度数
【分析】本题考查了平行线的性质,熟练掌握平行线的性质是解答本题的关键.先根据得,所以,再根据得,即可得解.
解:,
,
,
,
,
故选:C.
11.【考点】内错角相等两直线平行、同旁内角互补两直线平行、同位角相等两直线平行
【分析】本题主要考查了平行线的判定定理,熟练掌握平行线的判定定理是解题的关键;
根据平行线的判定定理逐项分析判断即可解答.
解:A、由只能推出,故错误,不符合题意;
B、由,只能推出,故错误,不符合题意;
C、,根据同旁内角互补,两直线平行,可以推出,故正确;
D、由,只能推出,故错误,不符合题意.
故选:C.
12.【考点】根据实际问题列二元一次方程组
【分析】本题考查了二元一次方程的应用,设桌面上的壹元硬币有枚,其中翻面前正面朝上的有枚,根据题意列出方程,理解题意,列出正确方程是解题的关键.
解:设桌面上的壹元硬币有枚,其中正面朝上的有枚,则正面向上的伍角硬币为枚,
由题可得,解得,
故选:A.
13.【考点】平行公理的应用
【分析】本题考查了平行公理推论,根据平行于同一条直线的两条直线平行即可求解,正确理解平行公理推论是解题的关键,
解:∵,,
∴,
理由:平行于同一条直线的两条直线平行,
故答案为:平行于同一条直线的两条直线平行.
14.【考点】加减消元法
【分析】用①-②可直接求解.
解:
①-②得:
x y=2
故答案为:2
【点评】本题考查的是解二元一次方程组——加减消元法,掌握加减消元的方法是关键.
15.【考点】有理数的乘方运算、幂的乘方的逆用、积的乘方的逆用
【分析】本题考查了幂的运算,解题的关键是熟练掌握相关运算法则.
先将化为,将化为,再根据积的乘方的逆运算进行计算即可.
解:
,
故答案为:.
16.【考点】三元一次方程组的应用
【分析】本题考查了三元一次方程组的应用.设这个生态牧场的原有草料a千克,每天生长b千克,每头牛每天可吃c千克草料,根据“这片草可供16头牛吃60天,或者供18头牛吃50天”,可列出关于a,b的三元一次方程组,解之可用含c的代数式表示出a,b的值,再将其代入中,即可求出结论.
解:设这个生态牧场的原有草料a千克,每天生长b千克,每头牛每天可吃c千克草料,
根据题意得:,
解得:,
∴(天),
∴这些割下来的草所制成的干草可供30头牛吃16天.
故答案为:16.
17.【考点】有理数的乘方运算、运用平方差公式进行运算
【分析】本题主要考查了平方差公式的应用,乘方的运算,熟练掌握平方差公式是解题关键.根据平方差公式,得出,从而得到的末位数字是,即可得到答案.
解:
,
的末位数是,
的末位数字是,即的末位数字是,
的末位数字是,
故答案为:.
18.【考点】平行线的性质在生活中的应用
【分析】本题考查了平行线的性质,根据两直线平行同位角相等得出,再由两直线平行同旁内角互补即可得出答案.
解:如图:
∵水中的两条光线平行,,
∴,
∵水面和杯底互相平行,
∴,
∵,
故答案为:.
19.【考点】代入消元法、加减消元法
【分析】本题主要考查了解二元一次方程组,熟练掌握解二元一次方程的消元思想是解题的关键.
(1)把①代入②得:,将y的值代入①即可求出x的值;
(2)可消去y求出x的值,将x的值代入①即可求出y的值.
解:(1)解:
把①代入②得:,
解得:,
把代入①得:,
∴原不等式组得解为.
(2)解:,
得:,
解得:,
把代入①得:,
∴,
∴原不等式组得解为.
20.【考点】积的乘方运算、计算单项式乘单项式、多项式乘多项式——化简求值、整式的混合运算
【分析】(1)先算乘方,再算乘法,后算加减,即可解答;
(2)利用多项式乘多项式,单项式乘多项式的法则进行计算,然后把,的值代入化简后的式子进行计算即可解答.
本题考查了整式的混合运算化简求值,准确熟练地进行计算是解题的关键.
解:(1)解:
;
(2)解:
,
当,时,
原式.
21.【考点】内错角相等两直线平行、根据平行线判定与性质求角度
【分析】本题主要考查了平行线的判定、平行线的性质,灵活运用平行线的判定定理和性质定理是解答本题的关键.
(1)由已知条件结合对顶角相等可得,然后根据内错角相等、两直线平行即可证明结论;
(2)先证明,再结合可得,进而证得,由平行线的性质可得,即,再结合求解即可解答.
(1)证明:∵,,,
∴,
∴.
(2)解:∵,,,
∴,
∵,
∴,
∴,
∴,,
∴①,
又∵②,
∴①②联立可得,
∴.
22.【考点】运用完全平方公式进行运算、通过对完全平方公式变形求值、拆项、添项、配方、待定系数法
【分析】本题主要考查了配方法求解代数式的最值问题,熟练掌握完全平方公式和平方的非负性是解题关键.
(1)将原式变形为,再利用平方的非负性即可求解;
(2)多次利用完全平方公式将原式变形,再利用平方的非负性即可求解.
解:(1)原式
,
当,时,
即,时,代数式有最小值为0;
(2)令,
则原式
,,
当时,代数式有最小值.
23.【考点】列代数式、整式加减的应用、多项式乘多项式与图形面积
【分析】本题考查了列代数式,整式加减的应用,有理数乘法的应用,理解题意并正确列式是解题关键.
(1)根据图形列式计算即可;
(2)先根据卫生间的面积求出,再计算出卧室以外的面积,乘以地砖的价格求解即可.
(1)解: 即该住宅的面积;
(2)解:由图形可知,卫生间的面积为,
卫生间的地面面积为,
,
,
卧室1的面积为,
卧室2的面积为,
卧室以外的面积为,
(元).
答:购买地砖至少需要花费4500元.
24.【考点】方案问题(二元一次方程组的应用)、二元一次方程的解
【分析】本题考查了二元一次方程组和二元一次方程的应用,根据题意,正确列出二元一次方程组及二元一次方程是解题的关键.
(1)设每辆型车、型车都载满货物一次可以分别运货吨、吨,根据题意,列出二元一次方程组即可求解;
(2)根据题意,列出二元一次方程,再根据都是正整数解答即可求解;
(3)分别求出每一种方案的费用即可求解;
解:(1)解:设每辆型车、型车都载满货物一次可以分别运货吨、吨,
依题意得,,
解得,
答:1辆型车载满货物一次可运3吨,1辆型车载满货物一次可运4吨;
(2)解:由(1)得,,
∴,
∵都是正整数,
∴或或,
∴有种租车方案:
方案一:型车10辆,型车1辆;
方案二:型车6辆,型车4辆;
方案三:型车2辆,型车7辆;
(3)解:∵型车每辆需租金100元/次,型车每辆需租金120元/次,
∴方案一需租金:元;
方案二需租金:元;
方案三需租金:元;
∵,
∴最省钱的租车方案是方案三,
答:租型车2辆,型车7辆,最少租车费为1040元.
25.【考点】加减消元法、三元一次方程组的应用
【分析】本题考查了二元一次方程组的应用,三元一次方程组的应用,掌握整体思想解决问题是解题的关键.
(1)将两方程相加可求的值,将两方程相减可求的值;
(2)由题意列出方程组,再计算出①②的结果,即可求解.
解:(1)解:,
①②可得:,
①②可得:;
(2)解:∵,
∴,
①②可得:.
26.【考点】平行公理的应用、根据平行线的性质探究角的关系
【分析】本题考查了平行线的性质和判定的应用,熟悉平行线的性质,作出合适的辅助线是解决问题的关键.
(1)过作,通过平行线性质求即可;
(2)过作交于,推出,根据平行线的性质得出,,即可得出答案;
(3)画出图形,根据平行线的性质得出,,即可得出答案.
解:(1)过点作,如图2所示,
,
,
,,
,,
,,
.
(2),
理由是:如图3,过作交于,
,
,
,,
;
(3)当在延长线时,如图所示,
,
,,
.
当在延长线时,如图所示,
,
,,
.
答案第2页,共2页
答案第1页,共3页
同课章节目录
