2024-2025学年人教版七年级(下)数学期末模拟试题(含解析)
文档属性
| 名称 | 2024-2025学年人教版七年级(下)数学期末模拟试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 377.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-05 00:00:00 | ||
图片预览


文档简介
2024-2025学年人教版七年级(下)数学期末模拟试题
姓名:__________班级:__________考号:__________总分__________
一 、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
如图,直线AB与CD相交于点O,OB平分∠DOE.若∠DOE=60 ,则∠AOE的度数是( )
A.90° B.150° C.180° D.不能确定
不等式组的解集,在数轴上表示正确的是( )
A. B.
C. D.
质检部门为了检测某品牌电器的质量,从同一批次共10 000件产品中随机抽取100件进行检测,检测出次品5件,由此估计这一批次产品中的次品件数是( )
A. 5 B. 100 C. 500 D. 10 000
在实数,0,,中,无理数是( )
A. B.0 C. D.
在平面直角坐标系中,将点(2,1)向右平移3个单位长度,则所得的点的坐标是( )
A.(0,5) B.(5,1) C.(2,4) D.(4,2)
为了改善住房条件,小亮的父母考察了某小区的A.B两套房.B房的面积比A房的面积大24平方米,两套楼房的总房价,A房和B房每平米的价格分别是平均价格的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设A房的面积为x平方米,B房的面积为y平方米,根据以上信息得出了下列方程组,其中正确的是( )
A. B.
C. D.
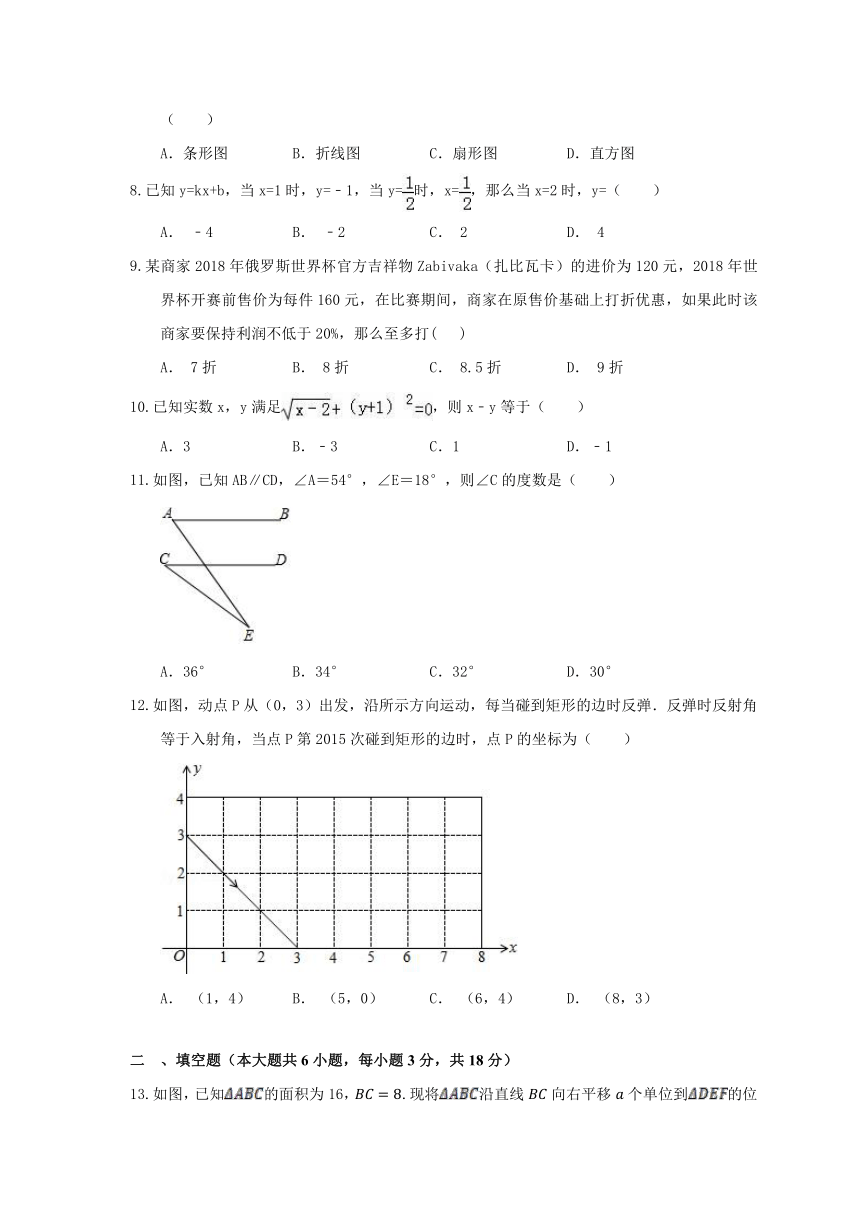
空气由多种气体混合而成,为了直观介绍空气中各成分的百分比,最适合使用的统计图是( )
A.条形图 B.折线图 C.扇形图 D.直方图
已知y=kx+b,当x=1时,y=﹣1,当y=时,x=,那么当x=2时,y=( )
A. ﹣4 B. ﹣2 C. 2 D. 4
某商家2018年俄罗斯世界杯官方吉祥物Zabivaka(扎比瓦卡)的进价为120元,2018年世界杯开赛前售价为每件160元,在比赛期间,商家在原售价基础上打折优惠,如果此时该商家要保持利润不低于20%,那么至多打( )
A. 7折 B. 8折 C. 8.5折 D. 9折
已知实数x,y满足,则x﹣y等于( )
A.3 B.﹣3 C.1 D.﹣1
如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A.36° B.34° C.32° D.30°
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
A. (1,4) B. (5,0) C. (6,4) D. (8,3)
二 、填空题(本大题共6小题,每小题3分,共18分)
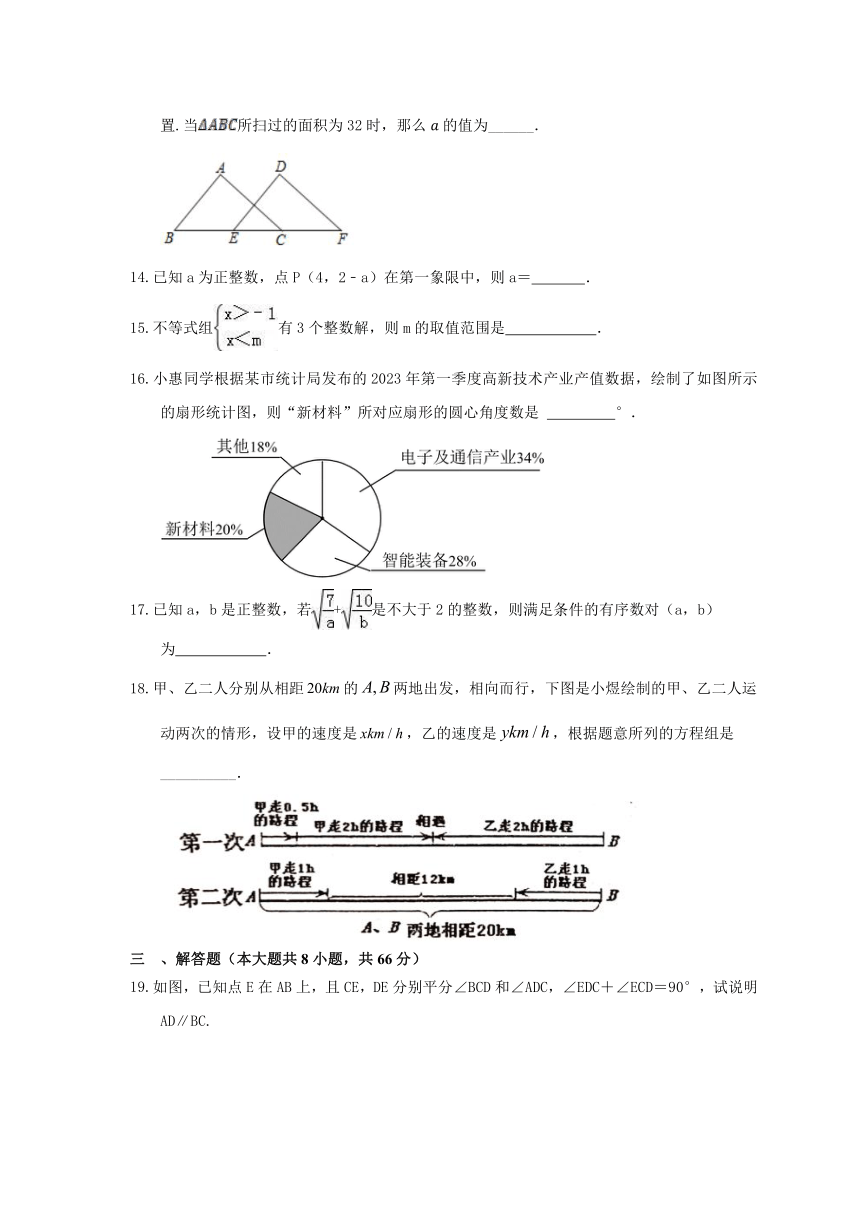
如图,已知的面积为16,.现将沿直线向右平移个单位到的位置.当所扫过的面积为32时,那么的值为______.
已知a为正整数,点P(4,2﹣a)在第一象限中,则a= .
不等式组有3个整数解,则m的取值范围是 .
小惠同学根据某市统计局发布的2023年第一季度高新技术产业产值数据,绘制了如图所示的扇形统计图,则“新材料”所对应扇形的圆心角度数是 °.
已知a,b是正整数,若+是不大于2的整数,则满足条件的有序数对(a,b)为 .
甲、乙二人分别从相距的两地出发,相向而行,下图是小煜绘制的甲、乙二人运动两次的情形,设甲的速度是,乙的速度是,根据题意所列的方程组是__________.
三 、解答题(本大题共8小题,共66分)
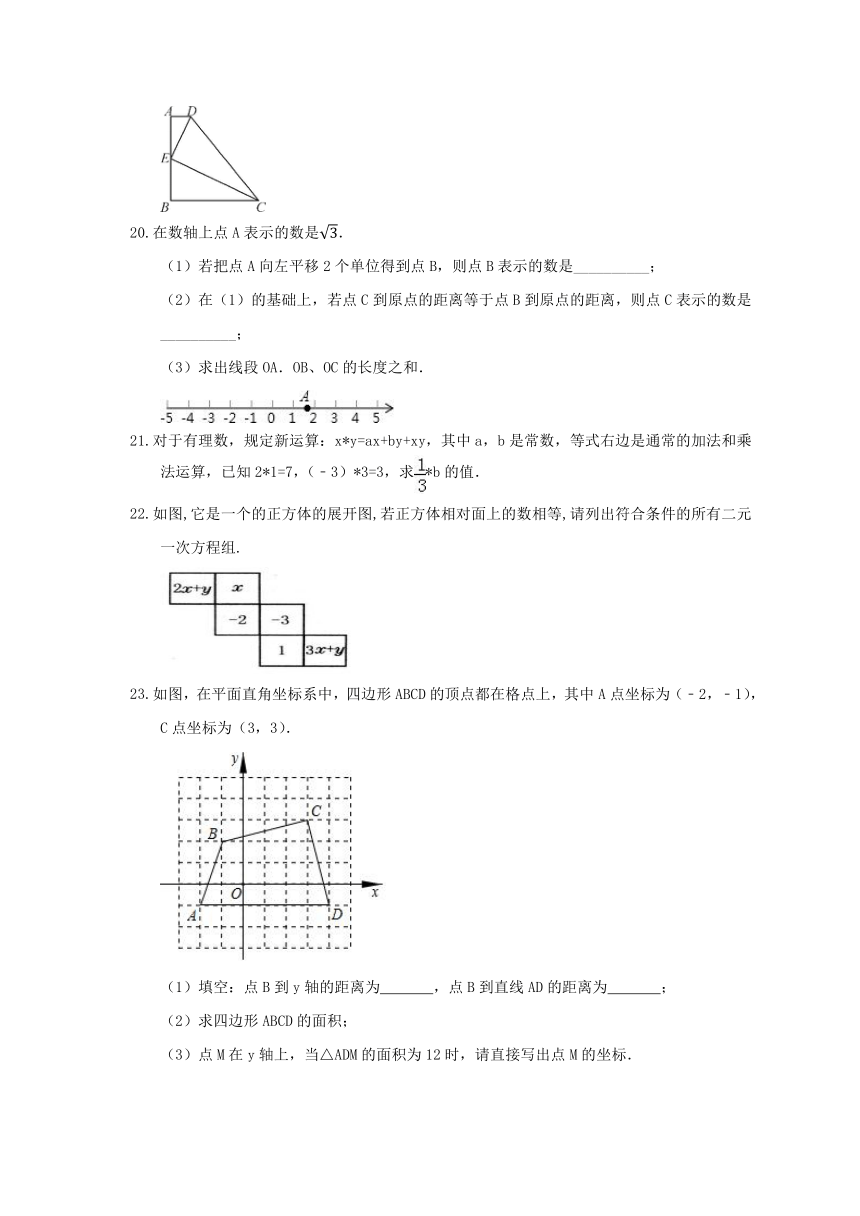
如图,已知点E在AB上,且CE,DE分别平分∠BCD和∠ADC,∠EDC+∠ECD=90°,试说明AD∥BC.
在数轴上点A表示的数是.
(1)若把点A向左平移2个单位得到点B,则点B表示的数是__________;
(2)在(1)的基础上,若点C到原点的距离等于点B到原点的距离,则点C表示的数是__________;
(3)求出线段OA.OB、OC的长度之和.
对于有理数,规定新运算:x*y=ax+by+xy,其中a,b是常数,等式右边是通常的加法和乘法运算,已知2*1=7,(﹣3)*3=3,求*b的值.
如图,它是一个的正方体的展开图,若正方体相对面上的数相等,请列出符合条件的所有二元一次方程组.
如图,在平面直角坐标系中,四边形ABCD的顶点都在格点上,其中A点坐标为(﹣2,﹣1),C点坐标为(3,3).
(1)填空:点B到y轴的距离为 ,点B到直线AD的距离为 ;
(2)求四边形ABCD的面积;
(3)点M在y轴上,当△ADM的面积为12时,请直接写出点M的坐标.
某电器超市销售每台进价分别为200元、170元的A.B两种型号的电风扇,下表是近两周的销售情况:
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 3台 5台 1800元
第二周 4台 10台 3100元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A.B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(如图1),并将调查结果绘制成图2和图3所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:
(1)求出本次接受调查的总人数,并将条形统计图补充完整;
(2)表示观点B的扇形的圆心角度数为 度;
(3)2016年底慈溪人口总数约为200万(含外来务工人员),请根据图中信息,估计慈溪市民认同观点D的人数.
(阅读探究)如图1,已知,分别是上的点,点在两平行线之间,,,求的度数.
解:过点作
∵
∴
∴
∴
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将和“凑”在一起,得出角之间的关系,使问题得以解决.进一步研究,我们可以发现图1中和之间存在一定的数量关系,请直接写出它们之间的数量关系: .
(方法运用)如图2,已知,点分别在直线上,点在两平线之间,求和之间的数量关系.
(应用拓展)如图3,在图2的条件下,作和的平分线、,交于点(交点在两平行线之间)若,求的度数.
答案解析
一 、选择题
【考点】邻补角,角平分线的定义
【分析】根据角平分线的性质可得∠BOE=30°,根据邻补角的定义可求∠AOE的度数.
解:∵OB平分∠DOE,
∴∠BOE∠DOE=30°.
∵∠AOE+∠BOE=180°,
∴∠AOE=180°﹣30°=150°.
故选B.
【点评】本题考查了邻补角,角平分线的定义,熟练掌握角平分线的定义是解答本题的关键.
【考点】解一元一次不等式组,在数轴上表示不等式组的解集
【分析】先求出每个不等式的解集,再求出不等式组的解集,即可得出选项.
解:
∵解不等式①得:x>-2,
解不等式②得:x≤2,
∴不等式组的解集为-2<x≤2,
在数轴上表示为,
故选:B.
【点评】本题考查了解一元一次不等式组和在数轴上表示不等式组的解集,能根据不等式的解集得出不等式组的解集是解此题的关键.
【考点】用样本估计总体
【分析】先求出次品所占的百分比,再根据生产这种零件10000件,直接相乘得出答案即可.
解:∵随机抽取100件进行检测,检测出次品5件,
∴次品所占的百分比是:,
∴这一批次产品中的次品件数是:10000×=500(件),
故选C.
【点评】此题主要考查了用样本估计总体,根据出现次品的数量求出次品所占的百分比是解题关键.
【考点】无理数
【分析】根据无理数的定义,即可求解.
解:在实数,0,,中,无理数是,
故选D.
【点评】本题主要考查无理数的定义,掌握“无限不循环小数是无理数”,是解题的关键.
【考点】坐标与图形变化﹣平移
【分析】在平面直角坐标系中,将点(2,1)向右平移时,横坐标增加,纵坐标不变.
解:将点(2,1)向右平移3个单位长度,则所得的点的坐标是(5,1).
故选:B.
【点评】本题运用了点平移的坐标变化规律,关键是把握好规律.
【考点】由实际问题抽象出二元一次方程组.
【分析】根据题意可得等量关系:①B房的面积比A房的面积大24平方米;②A房每平米的价格×1.1倍=B房每平米的价格×0.9倍,根据等量关系列出方程组即可.
【解答】解:设A房的面积为x平方米,B房的面积为y平方米,由题意得:
,
故选:D.
【点评】此题主要考查了有实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系,列出方程.
【考点】统计图的选择.
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目;
频数分布直方图,清楚显示在各个不同区间内取值,各组频数分布情况,易于显示各组之间频数的差别.
解:根据题意,得
要求直观反映空气的组成情况,即各部分在总体中所占的百分比,结合统计图各自的特点,应选择扇形统计图.
故选:C.
【点评】此题考查扇形统计图、折线统计图、条形统计图各自的特点.
【考点】 解二元一次方程组.
【分析】 将x与y的两对值代入y=kx+b中计算求出k与b的值,确定出关系式,将x=2代入即可求出y的值.
解:将x=1,y=1;x=,y=分别代入y=kx+b得:,
解得:k=1,b=0,
∴y=x,
将x=2代入得:y=2,
故选C
【点评】 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.
【考点】一元一次不等式的应用
【分析】设应打x折,根据吉祥物Zabivaka(扎比瓦卡)的进价为120元,售价为160元,准备打折出售,若保持利润不低于20%,可列不等式求解.
解:设应打x折,根据题意得,
160x-120≤120×20%
x≤0.9
即最多应该打9折.
故选:D.
【点评】本题考查理解题意的能力,关键根据利润=售价-进价,可列不等式求解.
【考点】非负数的性质:算术平方根;非负数的性质:偶次方.
【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.
解:根据题意得,x﹣2=0,y+1=0,
解得x=2,y=﹣1,
所以,x﹣y=2﹣(﹣1)=2+1=3.
故选A.
【点评】本题考查了算术平方根非负数,平方数非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.
【考点】平行线的性质
【分析】过点E作EF∥AB,则EF∥CD,由EF∥AB,利用“两直线平行,内错角相等”可得出∠AEF的度数,结合∠CEF=∠AEF-∠AEC可得出∠CEF的度数,由EF∥CD,利用“两直线平行,内错角相等”可求出∠C的度数.
解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,
∴∠AEF=∠A=54°,
∵∠CEF=∠AEF﹣∠AEC=54°﹣18°=36°.
又∵EF∥CD,
∴∠C=∠CEF=36°.
故选:A.
【点评】本题考查了平行线的性质,牢记“两直线平行,内错角相等”是解题的关键.
【考点】 规律型:点的坐标.
【分析】 根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2015除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图,经过6次反弹后动点回到出发点(0,3),
∵2015÷6=335…5,
∴当点P第2015次碰到矩形的边时为第336个循环组的第5次反弹,
点P的坐标为(1,4).
故选:A.
【点评】 本题考查了对点的坐标的规律变化的认识,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
二 、填空题
【考点】平移的性质
【分析】作AH⊥BC于H,根据△ABC的面积为16,BC=8,可先求出AH的长,△ABC所扫过的面积为32,继而求出a的值
解:△ABC所扫过面积即梯形ABFD的面积,作AH⊥BC于H,
∵S△ABC=16,∴BC AH=16,BC=8,AH=4,
∴S四边形ABFD=×(AD+BF)×AH
=(a+a+8)×4=32,
解得:a=4.
【点评】本题考查平移的性质,要求熟悉平移的性质以及等腰三角形的性质和直角三角形的性质.同时考查了学生综合运用数学的能力.
【考点】点的坐标.
【分析】根据平面直角坐标系中第一象限内的点的横、纵坐标都为正数,得到2﹣a>0,即可求出a的取值范围,再根据a为正整数即可得到a的值.
解:∵点P(4,2﹣a)在第一象限,
∴2﹣a>0,
∴a<2,
又a为正整数,
∴a=1.
故答案为:1.
【点评】本题主要考查了平面直角坐标系中点的坐标特征,熟知:第一象限内的点的坐标特征是(+,+),第二象限内的点的坐标特征是(﹣,+),第三象限内的点的坐标特征是(﹣,﹣),第四象限内的点的坐标特征是(+,﹣).
【考点】一元一次不等式组的整数解.
【分析】首先确定不等式组的整数解,然后根据只有这三个整数解即可确定.
解:不等式组的整数解是0,1,2.则m的取值范围是2<x≤3.
故答案是:2<x≤3.
【点评】本题考查了解一元一次不等式组的应用,关键是能根据不等式组的解集合已知得出关于m的不等式.
【考点】扇形统计图.
【分析】用360°乘“新材料”所占百分比20%即可.
解:新材料”所对应扇形的圆心角度数是:360°×20%=72°.
故答案为:72.
【点评】本题考查扇形统计图,解题的关键是将统计图中的信息有效关联起来.
【考点】实数及其运算,估算无理数的大小
【分析】根据二次根式的性质和已知得出即可.
解:∵ +是整数,
∴a=7,b=10或a=28,b=40,
因为当a=7,b=10时,原式=2是整数;
当a=28,b=40时,原式=1是整数;
即满足条件的有序数对(a,b)为(7,10)或(28,40),
故答案为:(7,10)或(28,40).
【点评】本题考查了二次根式的性质和二次根式的运算,估算无理数的大小的应用,题目比较好,有一定的难度.
【考点】由实际问题抽象出二元一次方程组
【分析】设甲的速度是xkm/h,乙的速度是ykm/h,根据路程=速度×时间结合两次运动的情形,即可得出关于x,y的二元一次方程组,此题得解.
解:设甲的速度是xkm/h,乙的速度是ykm/h,
依题意,得:.
故答案为:.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
三 、解答题
【考点】平行线的判定
【分析】由条件和角平分线的定义可得到∠ADC+∠BCD=180°,可判定AD∥BC.
解:∵CE,DE分别平分∠BCD和∠ADC,
∴∠BCD=2∠ECD,∠ADC=2∠EDC,
∵∠EDC+∠ECD=90°,
∴∠BCD+∠ADC=2∠ECD+2∠EDC=2(∠ECD+∠EDC)=2×90°=180°,
∴AD∥BC.
【点评】本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等 两直线平行,②内错角相等 两直线平行,③同旁内角互补 两直线平行,④a∥b,b∥c a∥c.
【考点】实数与数轴
【分析】(1)根据左减右加进行计算;
(2)关于原点对称的两个点互为相反数;
(3)求各点绝对值之和即可.
解:(1)点B表示的数是 2;
(2)点C到原点的距离等于点B到原点的距离,则点B和点C表示的数互为相反数,所以点C表示的数是2 ;
(3)由题可得:A表示,B表示–2,C表示2–,
∴OA=,OB=2–,OC=2–,
∴OA+OB+OC=+2–+2–=4–.
【点评】考查了实数与数轴之间的对应关系,解题关键是利用了数形结合分析问题.
【考点】解二元一次方程组.
【分析】先根据题意列出关于a、b的二元一次方程组,求出ab的值,再代入所求代数式进行计算即可.
解:∵x*y=ax+by+xy,2*1=7,(﹣3)*3=3,
∴,解得,
∴x*y=x+y+xy,
∴*6=×+×6+×6=.
【点评】本题考查的是解二元一次方程组,先根据题中所给的条件列出关于a、b的二元一次方程组是解答此题的关键.
【考点】二元一次方程组的运用
【分析】因为正方体相对面上的数相等,所以可将各式子和数值相组合,在进行求值,符合的即为本题答案.
解:∵正方体相对面上的数相等,
∴2x+y=-3,x=1,3x+y=-2.
∴可得到3个方程组:
【点评】本题考查了二元一次方程组的应用,熟练掌握该知识点是本题解题的关键.
【考点】坐标与图形的性质
【分析】(1)根据图形即可得到结论;
(2)根据矩形和三角形的面积公式即可得到结论;
(3)根据三角形的面积列方程即可得到结论.
解:(1)根据图形可知,B(﹣1,2),
∴点B到y轴的距离为1,点B到直线AD的距离为3;
故答案为:1,3;
(2)四边形ABCD的面积=6×4﹣×3×1﹣×4×1﹣×1×4-1=;
(3)设点M的坐标(0,m),
∵△ADM的面积为12,
∴×6×|m+1|=12,
∴m=3或-5,
∴M(0,﹣5),(0,3).
【点评】本题考查了三角形的面积,坐标与图形性质,正确的识别图形是解题的关键.
【考点】二元一次方程组的应用;一元一次方程的应用;一元一次不等式的应用.
【分析】(1)设A.B两种型号电风扇的销售单价分别为x元、y元,根据3台A型号5台B型号的电扇收入1800元,4台A型号10台B型号的电扇收入3100元,列方程组求解;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30﹣a)台,根据金额不多余5400元,列不等式求解;
(3)设利润为1400元,列方程求出a的值为20,不符合(2)的条件,可知不能实现目标.
解:(1)设A.B两种型号电风扇的销售单价分别为x元、y元,
依题意得:,
解得:,
答:A.B两种型号电风扇的销售单价分别为250元、210元;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30﹣a)台.
依题意得:200a+170(30﹣a)≤5400,
解得:a≤10.
答:超市最多采购A种型号电风扇10台时,采购金额不多于5400元;
(3)依题意有:(250﹣200)a+(210﹣170)(30﹣a)=1400,
解得:a=20,
∵a≤10,
∴在(2)的条件下超市不能实现利润1400元的目标.
【点评】本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程组和不等式求解.
【考点】条形统计图;用样本估计总体;扇形统计图.
【分析】(1)根据A类观点人数除以A类所占的百分比,可得调查的人数;根据各类调查的人数等于总人数,可得C类别人数,补全条形统计图;
(2)根据B类人数除以调查人数,再乘以360°,可得答案;
(3)用样本中观点D的人数所占比例乘以慈溪人口总数可得结论.
解:(1)2300÷46%=5000(人),故人口总数为5000人.
观点C的人数:5000×26%=1300人,
补全图形如下:
(2)表示观点B的扇形的圆心角度数为360°×=36°,
故答案为:36;
(3)200×=36(万人),
答:估计嘉善市民认同观点D的大约有36万人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
【考点】角平分线的定义,平行线的判定与性质
【分析】[阅读探究]过点M作MN∥AB,由平行线的性质等∠EMN=∠AEM=45°,∠FMN=∠CFM=25°,则∠EMF=∠EMN+∠FMN=∠AEM+∠CFM;
[方法运用]过点M作MN∥AB,由平行线的性质等∠EMN=∠BEM,∠FMN=∠DFM,再由平角的定义即可求解;
[应用拓展]过点P作PH∥AB,由平行线的性质得∠EPH=∠AEP,∠FPH=∠CFP,则∠EPF=(∠AEM+∠CFM),再由[方法运用]得∠EMF=360°-∠AEM-∠CFM,则∠AEM+∠CFM=360°-∠EMF=300°,进而求解即可.
解:[阅读探究]
过点M作MN∥AB,如图1所示:
∵AB∥CD,
∴MN∥CD,
∴∠EMN=∠AEM=45°,∠FMN=∠CFM=25°,
∴∠EMF=∠EMN+∠FMN=∠AEM+∠CFM,
故答案为:∠EMF=∠AEM+∠CFM;
[方法运用]
过点M作MN∥AB,如图2所示:
∵AB∥CD,
∴MN∥CD,
∴∠EMN=∠BEM,∠FMN=∠DFM,
∵∠BEM=180°-∠AEM,∠DFM=180°-∠CFM,
∴∠EMF=∠EMN+∠FMN=180°-∠AEM+180°-∠CFM=360°-∠AEM-∠CFM,
∴∠AEM、∠EMF和∠CFM之间的数量关系为:∠EMF=360°-∠AEM-∠CFM;
[应用拓展]
∵EP、FP分别是∠AEM和∠CFM的平分线,
∴∠AEP=∠AEM,∠CFP=∠CFM,
过点P作PH∥AB,如图3所示:
∵AB∥CD,
∴PH∥CD,
∴∠EPH=∠AEP,∠FPH=∠CFP,
∴∠EPF=∠EPH+∠FPH=∠AEP+∠CFP=∠AEM+∠CFM=(∠AEM+∠CFM),
由[方法运用]得:∠EMF=360°-∠AEM-∠CFM,
∴∠AEM+∠CFM=360°-∠EMF=360°-60°=300°,
∴(∠AEM+∠CFM)=×300°=150°,
∴∠EPF=150°.
【点评】本题考查了平行线的判定与性质、角平分线的性质以及平角的定义等知识,熟练掌握平行线的判定与性质,正确作出辅助线是解题的关键.
姓名:__________班级:__________考号:__________总分__________
一 、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
如图,直线AB与CD相交于点O,OB平分∠DOE.若∠DOE=60 ,则∠AOE的度数是( )
A.90° B.150° C.180° D.不能确定
不等式组的解集,在数轴上表示正确的是( )
A. B.
C. D.
质检部门为了检测某品牌电器的质量,从同一批次共10 000件产品中随机抽取100件进行检测,检测出次品5件,由此估计这一批次产品中的次品件数是( )
A. 5 B. 100 C. 500 D. 10 000
在实数,0,,中,无理数是( )
A. B.0 C. D.
在平面直角坐标系中,将点(2,1)向右平移3个单位长度,则所得的点的坐标是( )
A.(0,5) B.(5,1) C.(2,4) D.(4,2)
为了改善住房条件,小亮的父母考察了某小区的A.B两套房.B房的面积比A房的面积大24平方米,两套楼房的总房价,A房和B房每平米的价格分别是平均价格的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设A房的面积为x平方米,B房的面积为y平方米,根据以上信息得出了下列方程组,其中正确的是( )
A. B.
C. D.
空气由多种气体混合而成,为了直观介绍空气中各成分的百分比,最适合使用的统计图是( )
A.条形图 B.折线图 C.扇形图 D.直方图
已知y=kx+b,当x=1时,y=﹣1,当y=时,x=,那么当x=2时,y=( )
A. ﹣4 B. ﹣2 C. 2 D. 4
某商家2018年俄罗斯世界杯官方吉祥物Zabivaka(扎比瓦卡)的进价为120元,2018年世界杯开赛前售价为每件160元,在比赛期间,商家在原售价基础上打折优惠,如果此时该商家要保持利润不低于20%,那么至多打( )
A. 7折 B. 8折 C. 8.5折 D. 9折
已知实数x,y满足,则x﹣y等于( )
A.3 B.﹣3 C.1 D.﹣1
如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A.36° B.34° C.32° D.30°
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
A. (1,4) B. (5,0) C. (6,4) D. (8,3)
二 、填空题(本大题共6小题,每小题3分,共18分)
如图,已知的面积为16,.现将沿直线向右平移个单位到的位置.当所扫过的面积为32时,那么的值为______.
已知a为正整数,点P(4,2﹣a)在第一象限中,则a= .
不等式组有3个整数解,则m的取值范围是 .
小惠同学根据某市统计局发布的2023年第一季度高新技术产业产值数据,绘制了如图所示的扇形统计图,则“新材料”所对应扇形的圆心角度数是 °.
已知a,b是正整数,若+是不大于2的整数,则满足条件的有序数对(a,b)为 .
甲、乙二人分别从相距的两地出发,相向而行,下图是小煜绘制的甲、乙二人运动两次的情形,设甲的速度是,乙的速度是,根据题意所列的方程组是__________.
三 、解答题(本大题共8小题,共66分)
如图,已知点E在AB上,且CE,DE分别平分∠BCD和∠ADC,∠EDC+∠ECD=90°,试说明AD∥BC.
在数轴上点A表示的数是.
(1)若把点A向左平移2个单位得到点B,则点B表示的数是__________;
(2)在(1)的基础上,若点C到原点的距离等于点B到原点的距离,则点C表示的数是__________;
(3)求出线段OA.OB、OC的长度之和.
对于有理数,规定新运算:x*y=ax+by+xy,其中a,b是常数,等式右边是通常的加法和乘法运算,已知2*1=7,(﹣3)*3=3,求*b的值.
如图,它是一个的正方体的展开图,若正方体相对面上的数相等,请列出符合条件的所有二元一次方程组.
如图,在平面直角坐标系中,四边形ABCD的顶点都在格点上,其中A点坐标为(﹣2,﹣1),C点坐标为(3,3).
(1)填空:点B到y轴的距离为 ,点B到直线AD的距离为 ;
(2)求四边形ABCD的面积;
(3)点M在y轴上,当△ADM的面积为12时,请直接写出点M的坐标.
某电器超市销售每台进价分别为200元、170元的A.B两种型号的电风扇,下表是近两周的销售情况:
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 3台 5台 1800元
第二周 4台 10台 3100元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A.B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(如图1),并将调查结果绘制成图2和图3所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:
(1)求出本次接受调查的总人数,并将条形统计图补充完整;
(2)表示观点B的扇形的圆心角度数为 度;
(3)2016年底慈溪人口总数约为200万(含外来务工人员),请根据图中信息,估计慈溪市民认同观点D的人数.
(阅读探究)如图1,已知,分别是上的点,点在两平行线之间,,,求的度数.
解:过点作
∵
∴
∴
∴
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将和“凑”在一起,得出角之间的关系,使问题得以解决.进一步研究,我们可以发现图1中和之间存在一定的数量关系,请直接写出它们之间的数量关系: .
(方法运用)如图2,已知,点分别在直线上,点在两平线之间,求和之间的数量关系.
(应用拓展)如图3,在图2的条件下,作和的平分线、,交于点(交点在两平行线之间)若,求的度数.
答案解析
一 、选择题
【考点】邻补角,角平分线的定义
【分析】根据角平分线的性质可得∠BOE=30°,根据邻补角的定义可求∠AOE的度数.
解:∵OB平分∠DOE,
∴∠BOE∠DOE=30°.
∵∠AOE+∠BOE=180°,
∴∠AOE=180°﹣30°=150°.
故选B.
【点评】本题考查了邻补角,角平分线的定义,熟练掌握角平分线的定义是解答本题的关键.
【考点】解一元一次不等式组,在数轴上表示不等式组的解集
【分析】先求出每个不等式的解集,再求出不等式组的解集,即可得出选项.
解:
∵解不等式①得:x>-2,
解不等式②得:x≤2,
∴不等式组的解集为-2<x≤2,
在数轴上表示为,
故选:B.
【点评】本题考查了解一元一次不等式组和在数轴上表示不等式组的解集,能根据不等式的解集得出不等式组的解集是解此题的关键.
【考点】用样本估计总体
【分析】先求出次品所占的百分比,再根据生产这种零件10000件,直接相乘得出答案即可.
解:∵随机抽取100件进行检测,检测出次品5件,
∴次品所占的百分比是:,
∴这一批次产品中的次品件数是:10000×=500(件),
故选C.
【点评】此题主要考查了用样本估计总体,根据出现次品的数量求出次品所占的百分比是解题关键.
【考点】无理数
【分析】根据无理数的定义,即可求解.
解:在实数,0,,中,无理数是,
故选D.
【点评】本题主要考查无理数的定义,掌握“无限不循环小数是无理数”,是解题的关键.
【考点】坐标与图形变化﹣平移
【分析】在平面直角坐标系中,将点(2,1)向右平移时,横坐标增加,纵坐标不变.
解:将点(2,1)向右平移3个单位长度,则所得的点的坐标是(5,1).
故选:B.
【点评】本题运用了点平移的坐标变化规律,关键是把握好规律.
【考点】由实际问题抽象出二元一次方程组.
【分析】根据题意可得等量关系:①B房的面积比A房的面积大24平方米;②A房每平米的价格×1.1倍=B房每平米的价格×0.9倍,根据等量关系列出方程组即可.
【解答】解:设A房的面积为x平方米,B房的面积为y平方米,由题意得:
,
故选:D.
【点评】此题主要考查了有实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系,列出方程.
【考点】统计图的选择.
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目;
频数分布直方图,清楚显示在各个不同区间内取值,各组频数分布情况,易于显示各组之间频数的差别.
解:根据题意,得
要求直观反映空气的组成情况,即各部分在总体中所占的百分比,结合统计图各自的特点,应选择扇形统计图.
故选:C.
【点评】此题考查扇形统计图、折线统计图、条形统计图各自的特点.
【考点】 解二元一次方程组.
【分析】 将x与y的两对值代入y=kx+b中计算求出k与b的值,确定出关系式,将x=2代入即可求出y的值.
解:将x=1,y=1;x=,y=分别代入y=kx+b得:,
解得:k=1,b=0,
∴y=x,
将x=2代入得:y=2,
故选C
【点评】 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.
【考点】一元一次不等式的应用
【分析】设应打x折,根据吉祥物Zabivaka(扎比瓦卡)的进价为120元,售价为160元,准备打折出售,若保持利润不低于20%,可列不等式求解.
解:设应打x折,根据题意得,
160x-120≤120×20%
x≤0.9
即最多应该打9折.
故选:D.
【点评】本题考查理解题意的能力,关键根据利润=售价-进价,可列不等式求解.
【考点】非负数的性质:算术平方根;非负数的性质:偶次方.
【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.
解:根据题意得,x﹣2=0,y+1=0,
解得x=2,y=﹣1,
所以,x﹣y=2﹣(﹣1)=2+1=3.
故选A.
【点评】本题考查了算术平方根非负数,平方数非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.
【考点】平行线的性质
【分析】过点E作EF∥AB,则EF∥CD,由EF∥AB,利用“两直线平行,内错角相等”可得出∠AEF的度数,结合∠CEF=∠AEF-∠AEC可得出∠CEF的度数,由EF∥CD,利用“两直线平行,内错角相等”可求出∠C的度数.
解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,
∴∠AEF=∠A=54°,
∵∠CEF=∠AEF﹣∠AEC=54°﹣18°=36°.
又∵EF∥CD,
∴∠C=∠CEF=36°.
故选:A.
【点评】本题考查了平行线的性质,牢记“两直线平行,内错角相等”是解题的关键.
【考点】 规律型:点的坐标.
【分析】 根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2015除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图,经过6次反弹后动点回到出发点(0,3),
∵2015÷6=335…5,
∴当点P第2015次碰到矩形的边时为第336个循环组的第5次反弹,
点P的坐标为(1,4).
故选:A.
【点评】 本题考查了对点的坐标的规律变化的认识,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
二 、填空题
【考点】平移的性质
【分析】作AH⊥BC于H,根据△ABC的面积为16,BC=8,可先求出AH的长,△ABC所扫过的面积为32,继而求出a的值
解:△ABC所扫过面积即梯形ABFD的面积,作AH⊥BC于H,
∵S△ABC=16,∴BC AH=16,BC=8,AH=4,
∴S四边形ABFD=×(AD+BF)×AH
=(a+a+8)×4=32,
解得:a=4.
【点评】本题考查平移的性质,要求熟悉平移的性质以及等腰三角形的性质和直角三角形的性质.同时考查了学生综合运用数学的能力.
【考点】点的坐标.
【分析】根据平面直角坐标系中第一象限内的点的横、纵坐标都为正数,得到2﹣a>0,即可求出a的取值范围,再根据a为正整数即可得到a的值.
解:∵点P(4,2﹣a)在第一象限,
∴2﹣a>0,
∴a<2,
又a为正整数,
∴a=1.
故答案为:1.
【点评】本题主要考查了平面直角坐标系中点的坐标特征,熟知:第一象限内的点的坐标特征是(+,+),第二象限内的点的坐标特征是(﹣,+),第三象限内的点的坐标特征是(﹣,﹣),第四象限内的点的坐标特征是(+,﹣).
【考点】一元一次不等式组的整数解.
【分析】首先确定不等式组的整数解,然后根据只有这三个整数解即可确定.
解:不等式组的整数解是0,1,2.则m的取值范围是2<x≤3.
故答案是:2<x≤3.
【点评】本题考查了解一元一次不等式组的应用,关键是能根据不等式组的解集合已知得出关于m的不等式.
【考点】扇形统计图.
【分析】用360°乘“新材料”所占百分比20%即可.
解:新材料”所对应扇形的圆心角度数是:360°×20%=72°.
故答案为:72.
【点评】本题考查扇形统计图,解题的关键是将统计图中的信息有效关联起来.
【考点】实数及其运算,估算无理数的大小
【分析】根据二次根式的性质和已知得出即可.
解:∵ +是整数,
∴a=7,b=10或a=28,b=40,
因为当a=7,b=10时,原式=2是整数;
当a=28,b=40时,原式=1是整数;
即满足条件的有序数对(a,b)为(7,10)或(28,40),
故答案为:(7,10)或(28,40).
【点评】本题考查了二次根式的性质和二次根式的运算,估算无理数的大小的应用,题目比较好,有一定的难度.
【考点】由实际问题抽象出二元一次方程组
【分析】设甲的速度是xkm/h,乙的速度是ykm/h,根据路程=速度×时间结合两次运动的情形,即可得出关于x,y的二元一次方程组,此题得解.
解:设甲的速度是xkm/h,乙的速度是ykm/h,
依题意,得:.
故答案为:.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
三 、解答题
【考点】平行线的判定
【分析】由条件和角平分线的定义可得到∠ADC+∠BCD=180°,可判定AD∥BC.
解:∵CE,DE分别平分∠BCD和∠ADC,
∴∠BCD=2∠ECD,∠ADC=2∠EDC,
∵∠EDC+∠ECD=90°,
∴∠BCD+∠ADC=2∠ECD+2∠EDC=2(∠ECD+∠EDC)=2×90°=180°,
∴AD∥BC.
【点评】本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等 两直线平行,②内错角相等 两直线平行,③同旁内角互补 两直线平行,④a∥b,b∥c a∥c.
【考点】实数与数轴
【分析】(1)根据左减右加进行计算;
(2)关于原点对称的两个点互为相反数;
(3)求各点绝对值之和即可.
解:(1)点B表示的数是 2;
(2)点C到原点的距离等于点B到原点的距离,则点B和点C表示的数互为相反数,所以点C表示的数是2 ;
(3)由题可得:A表示,B表示–2,C表示2–,
∴OA=,OB=2–,OC=2–,
∴OA+OB+OC=+2–+2–=4–.
【点评】考查了实数与数轴之间的对应关系,解题关键是利用了数形结合分析问题.
【考点】解二元一次方程组.
【分析】先根据题意列出关于a、b的二元一次方程组,求出ab的值,再代入所求代数式进行计算即可.
解:∵x*y=ax+by+xy,2*1=7,(﹣3)*3=3,
∴,解得,
∴x*y=x+y+xy,
∴*6=×+×6+×6=.
【点评】本题考查的是解二元一次方程组,先根据题中所给的条件列出关于a、b的二元一次方程组是解答此题的关键.
【考点】二元一次方程组的运用
【分析】因为正方体相对面上的数相等,所以可将各式子和数值相组合,在进行求值,符合的即为本题答案.
解:∵正方体相对面上的数相等,
∴2x+y=-3,x=1,3x+y=-2.
∴可得到3个方程组:
【点评】本题考查了二元一次方程组的应用,熟练掌握该知识点是本题解题的关键.
【考点】坐标与图形的性质
【分析】(1)根据图形即可得到结论;
(2)根据矩形和三角形的面积公式即可得到结论;
(3)根据三角形的面积列方程即可得到结论.
解:(1)根据图形可知,B(﹣1,2),
∴点B到y轴的距离为1,点B到直线AD的距离为3;
故答案为:1,3;
(2)四边形ABCD的面积=6×4﹣×3×1﹣×4×1﹣×1×4-1=;
(3)设点M的坐标(0,m),
∵△ADM的面积为12,
∴×6×|m+1|=12,
∴m=3或-5,
∴M(0,﹣5),(0,3).
【点评】本题考查了三角形的面积,坐标与图形性质,正确的识别图形是解题的关键.
【考点】二元一次方程组的应用;一元一次方程的应用;一元一次不等式的应用.
【分析】(1)设A.B两种型号电风扇的销售单价分别为x元、y元,根据3台A型号5台B型号的电扇收入1800元,4台A型号10台B型号的电扇收入3100元,列方程组求解;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30﹣a)台,根据金额不多余5400元,列不等式求解;
(3)设利润为1400元,列方程求出a的值为20,不符合(2)的条件,可知不能实现目标.
解:(1)设A.B两种型号电风扇的销售单价分别为x元、y元,
依题意得:,
解得:,
答:A.B两种型号电风扇的销售单价分别为250元、210元;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30﹣a)台.
依题意得:200a+170(30﹣a)≤5400,
解得:a≤10.
答:超市最多采购A种型号电风扇10台时,采购金额不多于5400元;
(3)依题意有:(250﹣200)a+(210﹣170)(30﹣a)=1400,
解得:a=20,
∵a≤10,
∴在(2)的条件下超市不能实现利润1400元的目标.
【点评】本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程组和不等式求解.
【考点】条形统计图;用样本估计总体;扇形统计图.
【分析】(1)根据A类观点人数除以A类所占的百分比,可得调查的人数;根据各类调查的人数等于总人数,可得C类别人数,补全条形统计图;
(2)根据B类人数除以调查人数,再乘以360°,可得答案;
(3)用样本中观点D的人数所占比例乘以慈溪人口总数可得结论.
解:(1)2300÷46%=5000(人),故人口总数为5000人.
观点C的人数:5000×26%=1300人,
补全图形如下:
(2)表示观点B的扇形的圆心角度数为360°×=36°,
故答案为:36;
(3)200×=36(万人),
答:估计嘉善市民认同观点D的大约有36万人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
【考点】角平分线的定义,平行线的判定与性质
【分析】[阅读探究]过点M作MN∥AB,由平行线的性质等∠EMN=∠AEM=45°,∠FMN=∠CFM=25°,则∠EMF=∠EMN+∠FMN=∠AEM+∠CFM;
[方法运用]过点M作MN∥AB,由平行线的性质等∠EMN=∠BEM,∠FMN=∠DFM,再由平角的定义即可求解;
[应用拓展]过点P作PH∥AB,由平行线的性质得∠EPH=∠AEP,∠FPH=∠CFP,则∠EPF=(∠AEM+∠CFM),再由[方法运用]得∠EMF=360°-∠AEM-∠CFM,则∠AEM+∠CFM=360°-∠EMF=300°,进而求解即可.
解:[阅读探究]
过点M作MN∥AB,如图1所示:
∵AB∥CD,
∴MN∥CD,
∴∠EMN=∠AEM=45°,∠FMN=∠CFM=25°,
∴∠EMF=∠EMN+∠FMN=∠AEM+∠CFM,
故答案为:∠EMF=∠AEM+∠CFM;
[方法运用]
过点M作MN∥AB,如图2所示:
∵AB∥CD,
∴MN∥CD,
∴∠EMN=∠BEM,∠FMN=∠DFM,
∵∠BEM=180°-∠AEM,∠DFM=180°-∠CFM,
∴∠EMF=∠EMN+∠FMN=180°-∠AEM+180°-∠CFM=360°-∠AEM-∠CFM,
∴∠AEM、∠EMF和∠CFM之间的数量关系为:∠EMF=360°-∠AEM-∠CFM;
[应用拓展]
∵EP、FP分别是∠AEM和∠CFM的平分线,
∴∠AEP=∠AEM,∠CFP=∠CFM,
过点P作PH∥AB,如图3所示:
∵AB∥CD,
∴PH∥CD,
∴∠EPH=∠AEP,∠FPH=∠CFP,
∴∠EPF=∠EPH+∠FPH=∠AEP+∠CFP=∠AEM+∠CFM=(∠AEM+∠CFM),
由[方法运用]得:∠EMF=360°-∠AEM-∠CFM,
∴∠AEM+∠CFM=360°-∠EMF=360°-60°=300°,
∴(∠AEM+∠CFM)=×300°=150°,
∴∠EPF=150°.
【点评】本题考查了平行线的判定与性质、角平分线的性质以及平角的定义等知识,熟练掌握平行线的判定与性质,正确作出辅助线是解题的关键.
同课章节目录
