27.2.2相似三角形的性质 课件(共19张PPT) 人教版数学九年级下册
文档属性
| 名称 | 27.2.2相似三角形的性质 课件(共19张PPT) 人教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 713.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 20:12:41 | ||
图片预览



文档简介
(共19张PPT)
相似三角形的性质
年 级:九年级 学 科:数学(人教版)
课前复习
对应角相等、对应边成比例的三角形,叫做相似三角形.
1.平行于三角形一边的直线和其他两边(或延长线)相交所构成的三角形与原三角形相似
2.三边对应成比例的两个三角形相似
3.两边成比例且夹角相等的两个三角形相似
4.两角分别相等的两个三角形相似
5.斜边和一条直角边成比例的两个直角三角形相似
1相似三角形的概念
2三角形相似的判定
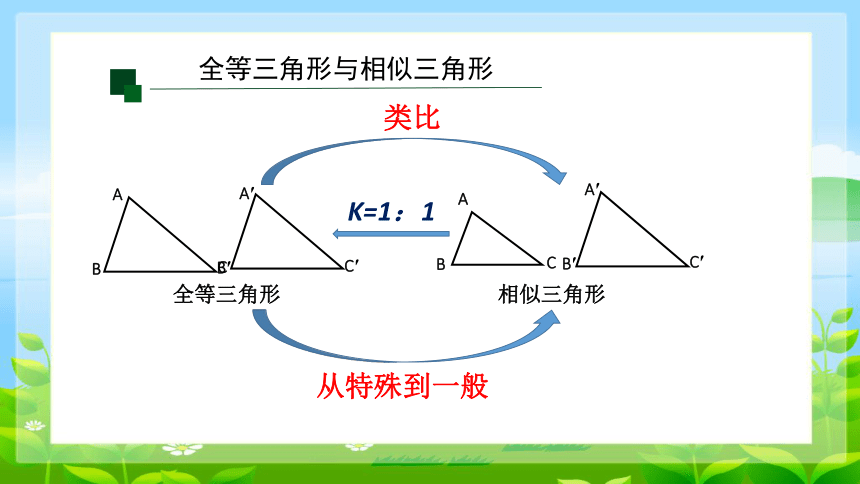
K=1:1
类比
从特殊到一般
B
C
A
B
C
A
B′
C′
A′
B′
C′
A′
全等三角形
相似三角形
全等三角形与相似三角形
类型 全等三角形的性质 相似三角形的性质
图形
边
角
三线
周长
面积
B
C
A
B′
C′
A′
类比探究相似三角形的性质
B
C
A
B′
C′
A′
对应边相等
对应角相等
对应高线、中线、
角平分线分别相等
周长相等
面积相等
对应边?
对应角?
对应高线、中线、角平分线
周长
面积
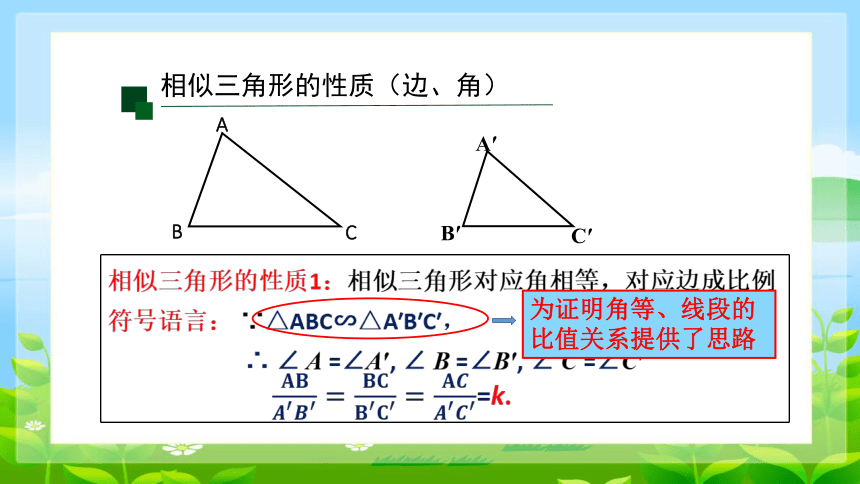
相似三角形的性质(边、角)
A
B
C
A′
B′
C′
相似三角形的性质1:相似三角形对应角相等,对应边成比例
符号语言: ∵△ABC∽△A′B′C′,
∴ ∠ A =∠A′, ∠ B =∠B′, ∠ C =∠C′
=k.
为证明角等、线段的比值关系提供了思路
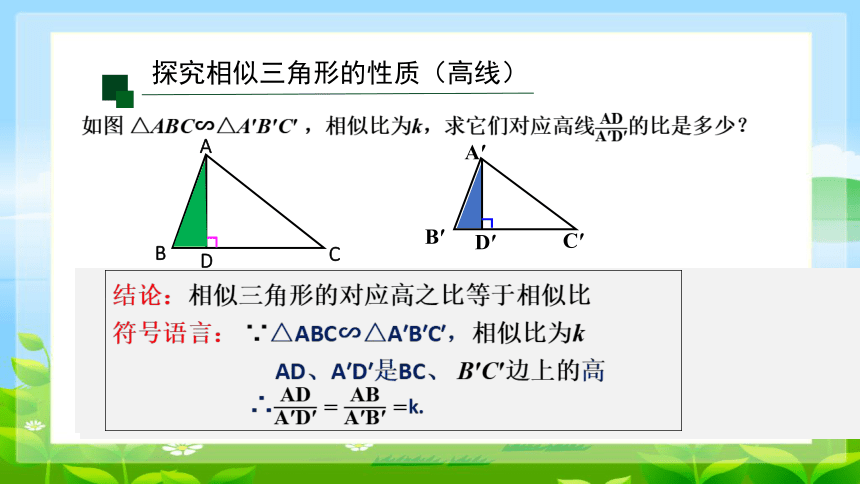
如图 △ABC∽△A′B′C′ ,相似比为k,求它们对应高线的比是多少?
A
B
C
D
A′
B′
C′
D′
分析:
已 知
探究相似三角形的性质(高线)
∠B =∠B ′
△ABC∽△A′B′C′
△ABD∽△A′B′D′
∠BDA=∠B′D′A′
两高
证明:∵ AD、A′D′是BC、 B′C′边上的高
∴ ∠BDA=∠B′D′A′=90°
又∵△ABC∽△A′B′C′ , ∴ ∠B =∠B′.
∴△ABD∽△A′B′D′.
∴ k.
结论:相似三角形的对应高之比等于相似比
符号语言: ∵△ABC∽△A′B′C′,相似比为k
AD、A′D′是BC、 B′C′边上的高
∴ k.
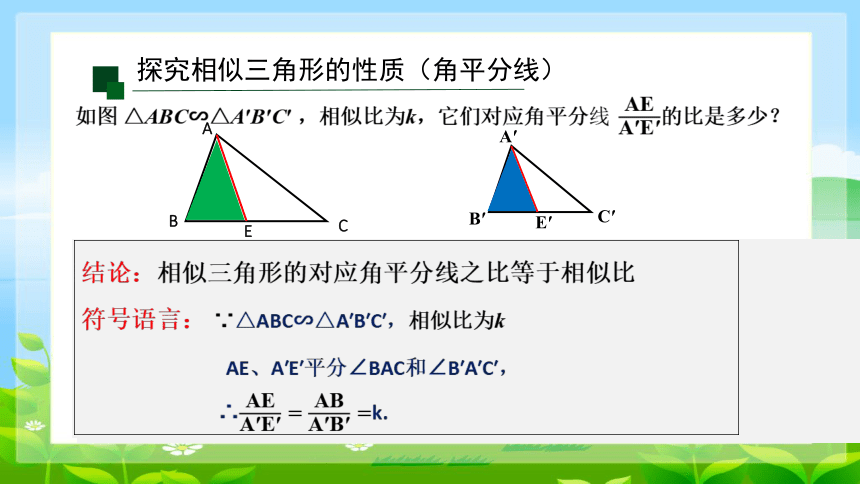
如图 △ABC∽△A′B′C′ ,相似比为k,它们对应角平分的比是多少?
A
B
C
E
A′
B′
C′
E′
探究相似三角形的性质(角平分线)
分析:
已 知
△ABE∽△A′B′E′
∠B =∠B ′,∠BAC=∠B′A′C′
△ABC∽△A′B′C′
两角平分线
∠BAE=∠B′A′E′
∴△ABE∽△A′B′E′
∴ k.
证明: ∵ △ABC∽△A′B′C′ ,
∴ ∠B =∠B′, ∠BAC=∠B′A′C′
又∵ AE、A′E′平分∠BAC和∠B′A′C′,
∴ ∠BAE=∠B′A′E′
结论:相似三角形的对应角平分线之比等于相似比
符号语言: ∵△ABC∽△A′B′C′,相似比为k
AE、A′E′平分∠BAC和∠B′A′C′,
∴ k.
A
B
C
F
如图, △ABC∽△A′B′C′ ,相似比为k,它们对应中的比是多少?
A′
B′
C′
F′
探究相似三角形的性质(中线)
分析:
已 知
△ABF∽△A′B′F′
∠B =∠B ′,k
△ABC∽△A′B′C′
两中线
k
证明: ∵ △ABC∽△A′B′C′ ,
∴ ∠B =∠B′.k
又∵A F、 A′ F′分别是BC、的中线,
∴k
∴△ABF∽△A′B′F′
∴ k.
结论:相似三角形的对应边上的中线之比等于相似比
符号语言: ∵△ABC∽△A′B′C′,相似比为k
A F、 A′ F′分别是BC、的中线,,
∴ k.
相似三角形的性质(三线)
A
B
C
A′
B′
C′
相似三角形的性质2:相似三角形对应高线、中线、角平分线之比都等于相似比
推广:相似三角形对应线段的比都等于相似比
连接对应
线段的桥梁
A
B
C
A′
B′
C′
如图,△ABC∽△A′B′C′,那么周长比也等于相似比吗?为什么?
分析:
△ABC∽△A′B′C′
已知
=k
探究相似三角形的性质(周长)
AB=kA′B′,BC=kB′C′,AC=kA′C′
证明:∵ △ABC ∽△A'B'C',相似比为 k
∴
∴ =k,
∴AB=kA′B′,BC=kB′C′,AC=kA′C′
结论:相似三角形的周长之比等于相似比
符号语言: ∵△ABC∽△A′B′C′,相似比为k
∴
A
B
C
D
A′
B′
C′
D′
如图,△ABC ∽△A′B′C′,那么面积比等于什么呢?
k
分析:
探究相似三角形的性质(面积)
已知
△ABC∽△A′B′C′
∴ =k .
证明:∵ △ABC ∽△A‘B’C‘,相似比为 k,
AD、A′D′分别是 BC、 B′C′边上高
结论:相似三角形的面积之比等于相似比的平方
符号语言: ∵△ABC∽△A′B′C′,
全等三角形的性质 类型 相似三角形的性质
图形
角
边
三线
周长
面积
B
C
A
B′
C′
A′
类比记忆相似三角形的性质
B
C
A
B′
C′
A′
对应角相等
面积之比等于相似比的平方
所有元素对应相等
对应线段及周长
之比等于相似比
【例1】填一填:
已知△ABC∽△DEF,若△ABC与△DEF的相似比为1:4,则△ABC与△DEF对应中线的比为 ,周长比为 .面积比为 .
相似三角形的性质的简单应用
1:4
1:4
1:2
1:16
1:2
变式1:已知△ABC∽△DEF,若△ABC与△DEF的面积比为1:4,则△ABC与△DEF对应中线的比为 ,周长比为 。
一组量的比
已知相似
其他对应量的比
相似三角形的性质的简单应用
变式2:如果把一个三角形各边同时扩大为原来的5 倍,那
么它的周长扩大为原来的____倍.,面积扩大为原来的___ 倍.
5
25
E
O
A
C
D
如图, △AOE∽△COD ,AE∶CD=1∶2.
(1)求△AOE与△COD的周长比;
(2)如果S△AOE=6 cm2,求△COD的面积.
B
相似三角形的性质的应用
解: (1)∵ △AOE∽△COD,AE∶CD=1∶2
∴ : =1:2
(2)∵ △AOE∽△COD, AE∶CD=1∶2
∴ S: =1:4
∵ S△AOE=6
∴ S=24 cm2
AE∥CD
AE:AB=1:2
解:(1) ∵四边形ABCD是平行四边形
∴ AB ∥ CD,AB=CD
∴ △AOE∽△COD,
又∵AE:AB=1:2 ∴ AE∶CD=1∶2
∴ : =1:2
(2)∵ △△AOE∽△COD,AE∶CD=1∶2
∴ S: =1:4
∵ S△AOE=6 ∴ S=24 cm2
在 ABCD中
相似三角形
的性质
对应角相等
对应线段的比等于相似比
周长比等于相似比
面积比等于相似比的平方
相似三角形
的判定
课堂小结
利用相似比求其他量
解决较复杂的问题
作业布置
(一)基础题
1.已知ΔABC与ΔA’B’C’的相似比为2:3,则周长比为 ,对应边上中线之比 ,面积之比为 .
2.如图, □ ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.
⑴求证:△ABF∽△CEB;
⑵若△DEF的面积为2,
求□ ABCD的面积.
B
A
F
E
D
C
作业布置
(二)实践题
(动手实践)如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A. B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为___cm. 你能用它测出小口瓶的内径吗?
同学们再见!
相似三角形的性质
年 级:九年级 学 科:数学(人教版)
课前复习
对应角相等、对应边成比例的三角形,叫做相似三角形.
1.平行于三角形一边的直线和其他两边(或延长线)相交所构成的三角形与原三角形相似
2.三边对应成比例的两个三角形相似
3.两边成比例且夹角相等的两个三角形相似
4.两角分别相等的两个三角形相似
5.斜边和一条直角边成比例的两个直角三角形相似
1相似三角形的概念
2三角形相似的判定
K=1:1
类比
从特殊到一般
B
C
A
B
C
A
B′
C′
A′
B′
C′
A′
全等三角形
相似三角形
全等三角形与相似三角形
类型 全等三角形的性质 相似三角形的性质
图形
边
角
三线
周长
面积
B
C
A
B′
C′
A′
类比探究相似三角形的性质
B
C
A
B′
C′
A′
对应边相等
对应角相等
对应高线、中线、
角平分线分别相等
周长相等
面积相等
对应边?
对应角?
对应高线、中线、角平分线
周长
面积
相似三角形的性质(边、角)
A
B
C
A′
B′
C′
相似三角形的性质1:相似三角形对应角相等,对应边成比例
符号语言: ∵△ABC∽△A′B′C′,
∴ ∠ A =∠A′, ∠ B =∠B′, ∠ C =∠C′
=k.
为证明角等、线段的比值关系提供了思路
如图 △ABC∽△A′B′C′ ,相似比为k,求它们对应高线的比是多少?
A
B
C
D
A′
B′
C′
D′
分析:
已 知
探究相似三角形的性质(高线)
∠B =∠B ′
△ABC∽△A′B′C′
△ABD∽△A′B′D′
∠BDA=∠B′D′A′
两高
证明:∵ AD、A′D′是BC、 B′C′边上的高
∴ ∠BDA=∠B′D′A′=90°
又∵△ABC∽△A′B′C′ , ∴ ∠B =∠B′.
∴△ABD∽△A′B′D′.
∴ k.
结论:相似三角形的对应高之比等于相似比
符号语言: ∵△ABC∽△A′B′C′,相似比为k
AD、A′D′是BC、 B′C′边上的高
∴ k.
如图 △ABC∽△A′B′C′ ,相似比为k,它们对应角平分的比是多少?
A
B
C
E
A′
B′
C′
E′
探究相似三角形的性质(角平分线)
分析:
已 知
△ABE∽△A′B′E′
∠B =∠B ′,∠BAC=∠B′A′C′
△ABC∽△A′B′C′
两角平分线
∠BAE=∠B′A′E′
∴△ABE∽△A′B′E′
∴ k.
证明: ∵ △ABC∽△A′B′C′ ,
∴ ∠B =∠B′, ∠BAC=∠B′A′C′
又∵ AE、A′E′平分∠BAC和∠B′A′C′,
∴ ∠BAE=∠B′A′E′
结论:相似三角形的对应角平分线之比等于相似比
符号语言: ∵△ABC∽△A′B′C′,相似比为k
AE、A′E′平分∠BAC和∠B′A′C′,
∴ k.
A
B
C
F
如图, △ABC∽△A′B′C′ ,相似比为k,它们对应中的比是多少?
A′
B′
C′
F′
探究相似三角形的性质(中线)
分析:
已 知
△ABF∽△A′B′F′
∠B =∠B ′,k
△ABC∽△A′B′C′
两中线
k
证明: ∵ △ABC∽△A′B′C′ ,
∴ ∠B =∠B′.k
又∵A F、 A′ F′分别是BC、的中线,
∴k
∴△ABF∽△A′B′F′
∴ k.
结论:相似三角形的对应边上的中线之比等于相似比
符号语言: ∵△ABC∽△A′B′C′,相似比为k
A F、 A′ F′分别是BC、的中线,,
∴ k.
相似三角形的性质(三线)
A
B
C
A′
B′
C′
相似三角形的性质2:相似三角形对应高线、中线、角平分线之比都等于相似比
推广:相似三角形对应线段的比都等于相似比
连接对应
线段的桥梁
A
B
C
A′
B′
C′
如图,△ABC∽△A′B′C′,那么周长比也等于相似比吗?为什么?
分析:
△ABC∽△A′B′C′
已知
=k
探究相似三角形的性质(周长)
AB=kA′B′,BC=kB′C′,AC=kA′C′
证明:∵ △ABC ∽△A'B'C',相似比为 k
∴
∴ =k,
∴AB=kA′B′,BC=kB′C′,AC=kA′C′
结论:相似三角形的周长之比等于相似比
符号语言: ∵△ABC∽△A′B′C′,相似比为k
∴
A
B
C
D
A′
B′
C′
D′
如图,△ABC ∽△A′B′C′,那么面积比等于什么呢?
k
分析:
探究相似三角形的性质(面积)
已知
△ABC∽△A′B′C′
∴ =k .
证明:∵ △ABC ∽△A‘B’C‘,相似比为 k,
AD、A′D′分别是 BC、 B′C′边上高
结论:相似三角形的面积之比等于相似比的平方
符号语言: ∵△ABC∽△A′B′C′,
全等三角形的性质 类型 相似三角形的性质
图形
角
边
三线
周长
面积
B
C
A
B′
C′
A′
类比记忆相似三角形的性质
B
C
A
B′
C′
A′
对应角相等
面积之比等于相似比的平方
所有元素对应相等
对应线段及周长
之比等于相似比
【例1】填一填:
已知△ABC∽△DEF,若△ABC与△DEF的相似比为1:4,则△ABC与△DEF对应中线的比为 ,周长比为 .面积比为 .
相似三角形的性质的简单应用
1:4
1:4
1:2
1:16
1:2
变式1:已知△ABC∽△DEF,若△ABC与△DEF的面积比为1:4,则△ABC与△DEF对应中线的比为 ,周长比为 。
一组量的比
已知相似
其他对应量的比
相似三角形的性质的简单应用
变式2:如果把一个三角形各边同时扩大为原来的5 倍,那
么它的周长扩大为原来的____倍.,面积扩大为原来的___ 倍.
5
25
E
O
A
C
D
如图, △AOE∽△COD ,AE∶CD=1∶2.
(1)求△AOE与△COD的周长比;
(2)如果S△AOE=6 cm2,求△COD的面积.
B
相似三角形的性质的应用
解: (1)∵ △AOE∽△COD,AE∶CD=1∶2
∴ : =1:2
(2)∵ △AOE∽△COD, AE∶CD=1∶2
∴ S: =1:4
∵ S△AOE=6
∴ S=24 cm2
AE∥CD
AE:AB=1:2
解:(1) ∵四边形ABCD是平行四边形
∴ AB ∥ CD,AB=CD
∴ △AOE∽△COD,
又∵AE:AB=1:2 ∴ AE∶CD=1∶2
∴ : =1:2
(2)∵ △△AOE∽△COD,AE∶CD=1∶2
∴ S: =1:4
∵ S△AOE=6 ∴ S=24 cm2
在 ABCD中
相似三角形
的性质
对应角相等
对应线段的比等于相似比
周长比等于相似比
面积比等于相似比的平方
相似三角形
的判定
课堂小结
利用相似比求其他量
解决较复杂的问题
作业布置
(一)基础题
1.已知ΔABC与ΔA’B’C’的相似比为2:3,则周长比为 ,对应边上中线之比 ,面积之比为 .
2.如图, □ ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.
⑴求证:△ABF∽△CEB;
⑵若△DEF的面积为2,
求□ ABCD的面积.
B
A
F
E
D
C
作业布置
(二)实践题
(动手实践)如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A. B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为___cm. 你能用它测出小口瓶的内径吗?
同学们再见!
