2025年九年级中考数学三轮冲刺训练相似三角形的判定与性质训练(含答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练相似三角形的判定与性质训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 703.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 15:03:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练相似三角形的判定与性质训练
1.如图,在△ABC中,AB=AC,D为BC边上一点,E为AC边上一点,且∠ADE=∠B.
(1)求证:△ABD∽△DCE;
(2)若AC=12,BC=11,CE=2,求BD的长.
2.如图,△ABC中,点D,E,F分别在AB,BC,AC边上DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)设.
①若BC=20,求线段BE的长;
②若△EFC的面积是20,求四边形ADEF的面积.
3.如图,Rt△ABC中,∠B=90°,AB=6,BC=8,D是斜边AC上一个动点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF.
(1)求证:四边形BEDF是矩形;
(2)若四边形BEDF为正方形,求的值.
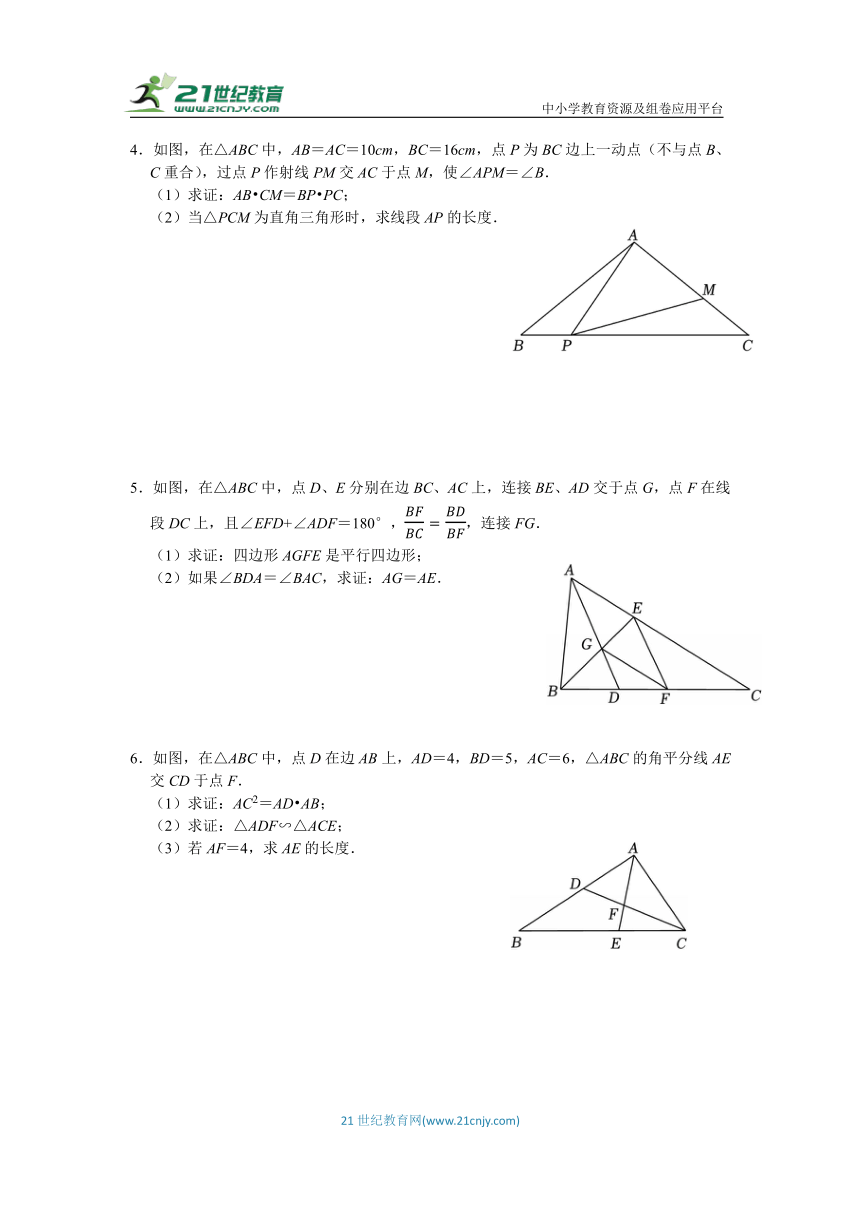
4.如图,在△ABC中,AB=AC=10cm,BC=16cm,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B.
(1)求证:AB CM=BP PC;
(2)当△PCM为直角三角形时,求线段AP的长度.
5.如图,在△ABC中,点D、E分别在边BC、AC上,连接BE、AD交于点G,点F在线段DC上,且∠EFD+∠ADF=180°,,连接FG.
(1)求证:四边形AGFE是平行四边形;
(2)如果∠BDA=∠BAC,求证:AG=AE.
6.如图,在△ABC中,点D在边AB上,AD=4,BD=5,AC=6,△ABC的角平分线AE交CD于点F.
(1)求证:AC2=AD AB;
(2)求证:△ADF∽△ACE;
(3)若AF=4,求AE的长度.
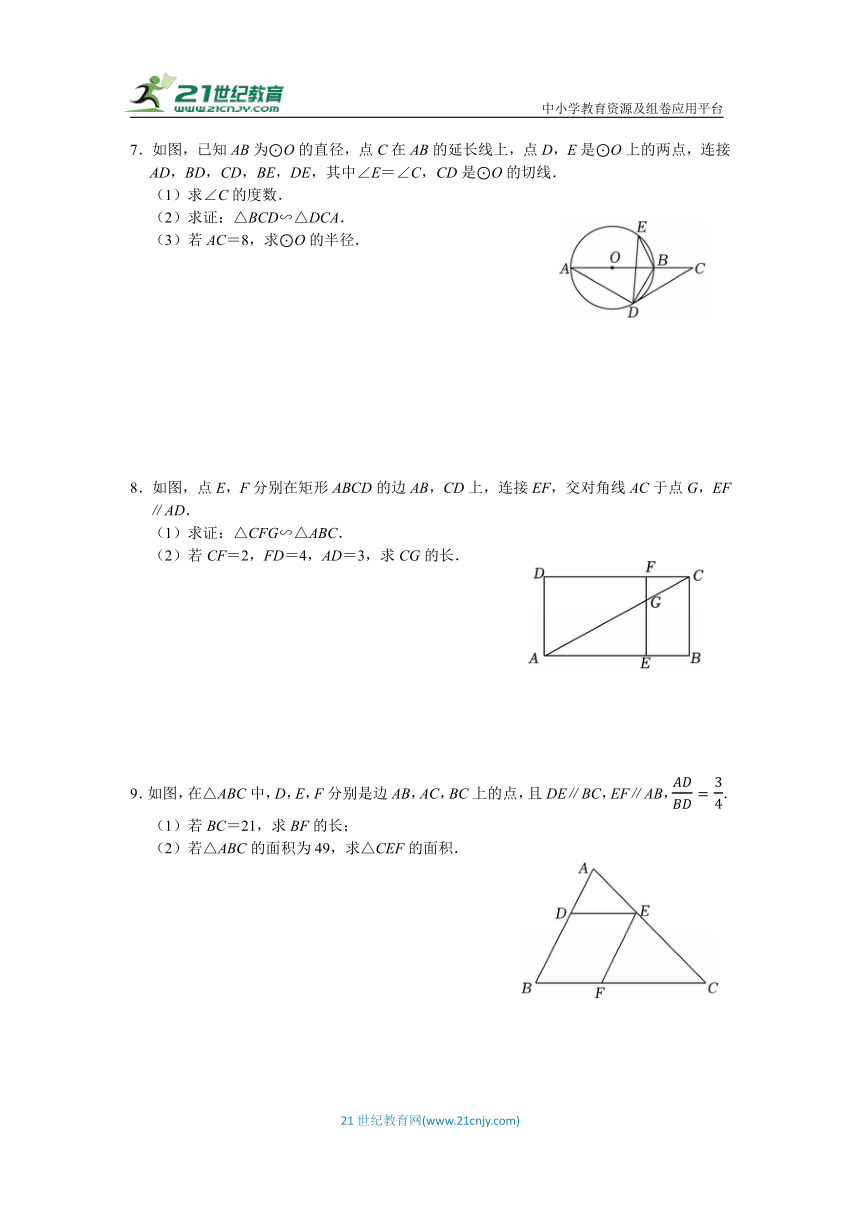
7.如图,已知AB为⊙O的直径,点C在AB的延长线上,点D,E是⊙O上的两点,连接AD,BD,CD,BE,DE,其中∠E=∠C,CD是⊙O的切线.
(1)求∠C的度数.
(2)求证:△BCD∽△DCA.
(3)若AC=8,求⊙O的半径.
8.如图,点E,F分别在矩形ABCD的边AB,CD上,连接EF,交对角线AC于点G,EF∥AD.
(1)求证:△CFG∽△ABC.
(2)若CF=2,FD=4,AD=3,求CG的长.
9.如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,.
(1)若BC=21,求BF的长;
(2)若△ABC的面积为49,求△CEF的面积.
10.如图,点E是矩形ABCD中AD边上一点,△ABE沿BE折叠为△FBE,点F落在CD上.(1)求证:△CFB∽△DEF;
(2)若,BCcm,求BF的值.
11.正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:△ABM∽△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;
(3)求梯形ABCN的面积最大时,点M的位置.
12.如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E作EF⊥ED交AB于点G、交DA延长线于点F.
(1)求证:△ECD∽△DEF;
(2)若CD=4,求AF的长.
13.已知:如图,在△ABC中,D是BC的中点,AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)求证:AF=DF;
(3)若△FCD的面积为5,BC=10,求DE的长.
14.如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交BE于M,FD、AC的延长线交于点N.
(1)求证:△BFM∽△NFA;
(2)求证:DF2=FM FN;
(3)若AC=BC,DN=12,ME:EN=1:2,求线段AC的长.
15.如图,在△ABC中,点E为AB边上一点,分别过点B,E作BD∥AC,EF∥AC,BD交CE的延长线于点D,EF交BC于点F,且AC=6,BD=4.
(1)求EF的长;
(2)若△BEF的面积为4,求△CEF的面积.
16.如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F.
(1)若BE平分∠CBD,求证:BF⊥AC;
(2)找出图中与△OBF相似的三角形,并说明理由;
(3)若OF=3,EF=2,求DE的长度.
17.如图1,在△ABC中,BD平分∠ABC,BD=CD,AB=4,AC=6.
(1)求CD的长;
(2)如图2,在(1)的条件下,E为BC上的点,作∠AEF=∠ABC交AC于点F,AE、BD相交于点G.
①求证:△ABG∽△ECF;
②若BG=2CF,求.
参考答案
1.【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,
∵∠ADE=∠B,
∴∠BAD=∠CDE,
∴△ABD∽△CDE;
(2)解:∵AB=AC,AC=12,
∴AB=12,
由(1)知,△ABD∽△CDE,
∴=即=,
∴BD=3或8.
2.【解答】(1)证明:由已知条件可知:DE∥AC,EF∥AB,
根据平行线的性质可得:∠BED=∠ECF,∠FEC=∠DBE,
∴△BDE∽△EFC;
(2)解:①∵EF∥AB,
∴,
∴,
∵BC=20.
∴.
②解:∵,
∵△EFC的面积是20,
∴S△BDE=5,
∵EF∥AB,,
∴△ABC∽△EFC,,
∴,
∴S△ABC=45,
∴面积为S△ABC﹣S△EFC﹣S△BDE=45﹣5﹣20=20.
3.【解答】(1)证明:∵DE⊥AB于点E,DF⊥BC于点F,
∴∠BED=∠BFD=90°,
∵∠B=90°,
∴四边形BEDF是矩形;
(2)解:∵四边形BEDF为正方形,
∴DE=DF=BE=BF,
设DE=DF=BE=BF=x,则AE=6﹣x,
∵,
∴,
∴x,
经检验,x是原方程的解,
∴AE,
∴AD,
∵AC,
∴DC=AC﹣AD,
∴.
4.【解答】(1)证明:∵AB=AC=10cm,
∴∠B=∠C,
∵∠APM+∠CPM=∠APC=∠B+∠BAP,∠APM=∠B,
∴∠CPM=∠BAP,
∴△CPM∽△BAP,
∴,
∴AB CM=BP PC;
(2)解:∵∠B=∠C≠90°,
当∠PMC=90°时,如图,
由(1)知△CPM∽△BAP,
∴∠APB=∠PMC=90°,
∵AB=AC,
∴点P为BC中点,
∴BP=CP==8(cm),
∴ap==6(cm);
当∠CPM=90°时,如图,作AD⊥BC于点D,则AD=6cm,
由(1)知△CPM∽△BAP,
∴∠BAP=∠CPM=90°,
∵AB=AC,AD⊥BC,
∴,
∵∠BAP=∠BDA=90°,∠ABP=∠DBA,
∴△ABP∽△DBA,
∴,
∴AP=(cm),
综上可知,线段AP的长度为6cm或.
5.【解答】证明:(1)∵∠EFD+∠ADF=180°,
∴AD∥EF,
∴,
又∵,
∴,
∵∠DBG=∠CBE,
∴△BFG∽△BCE,
∴∠BFG=∠BCE,
∴GF∥AC,
∴四边形AGFE是平行四边形;
(2)由(1)得四边形AGFE是平行四边形,∠BDA=∠BAC,且∠ABD=∠ABC,如图,连接AF交GE于点O,
∴OA=OF,△ABD∽△CBA,
∴,即AB2=BC BD,
∵,即BF2=BC BD,
∴AB=BF,
∴BO⊥AF,
即:AF⊥GE,
∴四边形AGFE是菱形,
∴AG=AE.
6.【解答】(1)证明:∵AD=4,BD=5,
∴AB=AD+BD=4+5=9,
∴AC2=62=36,AB AD=9×4=36,
∴AC2=AD AB;
(2)证明:∵AC2=AD AB,
∴,
又∵∠BAC=∠CAD,
∴△ABC∽△ACD,
∴∠ACB=∠ADC,
∵AE平分∠BAC,
∴∠DAF=∠CAE,
∴△DAF∽△CAE;
(3)解:∵△DAF∽△CAE,
∴,
∵AF=4,
∴AE6.
7.【解答】(1)解:连接OD,如图,
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠ODC=90°,
∵∠BOD=2∠E,∠E=∠C,
∴∠BOD=2∠C,
而∠BOD+∠C=90°,
即2∠C+∠C=90°,
∴∠C=30°;
(2)证明:∵AB为直径,
∴∠ADB=90°,
∵∠ADO+∠ODB=90°,∠BDC+∠ODB=90°,
∴∠ADO=∠BDC,
∵OA=OD,
∴∠ADO=∠A,
∴∠BDC=∠A,
∵∠BCD=∠DCA,
∴△BCD∽△DCA;
(3)解:设⊙O的半径为r,则OA=OD=r,OC=8﹣r,
在Rt△OCD中,∵∠C=30°,
∴OC=2OD,
即8﹣r=2r,
解得r,
即⊙O的半径为.
8.【解答】(1)证明:∵EF∥AD,
∴∠CFG=∠D,
∵四边形ABCD是矩形,
∴∠D=∠B,CD∥AB,
∴∠CFG=∠B,∠FCG=∠BAC,
∴△CFG∽△ABC.
(2)解:∵CF=2,FD=4,AD=3,
∴CD=CF+FD=2+4=6,
∵∠D=90°,
∴CA3,
∵GF∥AD,
∴△CFG∽△CDA,
∴,
∴CGCA3,
∴CG的长是.
9.【解答】解:(1)∵DE∥BC,
∴.
∵EF∥AB,
∴,
∴.
设CF=4k,则BF=3k,则CF=4k.
∵BC=21,
∴3k+4k=21,
解得k=3,
∴BF=3k=9;
(2)由(1),得,
∴.
∵EF∥AB,
∴△ABC∽△EFC.
∵,S△ABC=49,
∴S△CEF=16.
10.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠C=∠D=90°,
∴∠CBF+∠CFB=90°,
∵△ABE沿BE折叠为△FBE,
∴∠EFB=∠A=90°,
∴∠DFE+∠CFB=90°,
∴∠DFE=∠CBF,
∴△CFB∽△DEF;
(2)解:由(1)得:△CFB∽△DEF,
∴,
设CF=k,BF=3k(k>0),
∵BF2﹣CF2=BC2,,
∴,
∴k1=2,k2=﹣2(舍去),
∴BF=3k=6cm.
11.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°,
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,
∴△ABM∽△MCN;
(2)解:∵△ABM∽△MCN,
∴,即,
∴,
∴;
(3)解:,
∵,
∴y有最大值,且当x=2时,y取得最大值,最大值为10,
即当点M运动到BC中点时,梯形ABCN的面积最大,最大值为10.
12.【解答】(1)证明:∵在正方形ABCD中,EF⊥ED,
∴∠FED=∠C=90°,
∵BC∥AD,
∴∠CED=∠FDE,
∴△ECD∽△DEF;
(2)解:∵四边形ABCD是正方形,
∴∠C=90°,AD=BC=CD=4,
∵E为BC的中点,
∴CE=0.5BC=2
在Rt△DCE中,
由勾股定理得:DE2=CE2+DC2=22+42=20,
∵△ECD∽△DEF,
∴CE:DE=DE:DF,
∴2:DE=DE:DF,
2DF=DE2,
解得:DF=10,
∵AD=4,
∴AF=DF﹣AD=10﹣4=6.
13.【解答】(1)证明:在△ABC中,D是BC的中点,AD=AC,DE⊥BC,
∴BD=CD,∠ACB=∠FDC,
∴EB=EC,
∴∠ABC=∠FCD,
∴△ABC∽△FCD;
(2)证明:∵△ABC∽△FCD,
∴,
∵AD=AC,BC=2CD,
∴,
∴AF=DF.
(3)解:△FCD的面积为5,BC=10,如图,作AM⊥BC于M,
∵△ABC∽△FCD,
∴,
∴S△ABC=4S△FCD=20,
∵S△ABCBC AM10 AM,
∴AM=4,
∴DM,BM,
∵DE∥AM,
∴,
∴DE BM=AM BD,
即:,
∴.
14.【解答】(1)证明∵DF⊥AB,AD,BE是△ABC的高,
∴∠BFD=∠AFD=∠AEB=∠ADB=90°,
∴∠FBM=90°﹣∠BAC,∠N=90°﹣∠BAC,
∴∠FBM=∠N,
又∵∠BFD=∠AFD,
∴△BFM∽△NFA;
(2)证明:∵△BFM∽△NFA,
∴,
∴FM FN=FB FA,
∵∠FBD+∠FDB=90°,∠FBD+∠FAD=90°,
∴∠FDB=∠FAD,
∵∠BFD=∠AFD,∠FDB=∠FAD,
∴△BFD∽△DFA,
∴,
∴DF2=FM FN;
(3)解:∵AC=BC,
∴∠BAC=∠ABC,
∵∠ABC+∠FDB=∠BAC+∠N=90°,
∴∠FDB=∠N=∠FBM,
∴△ENM∽△FBM∽△FDB,
∴,
∴FB=2FM,FD=2FB=4FM,
∵DF2=FM FN,
∴(4FM)2=FM (4FM+12),
解得:FM=1或0(舍去),
∴FB=2,FD=4,FN=FD+DN=16,
∵,
∴AF=8,AB=AF+BF=10,
在Rt△BFD中,
BD2,
在Rt△ADB与Rt△ADC中,
AD2=AB2﹣BD2=AC2﹣CD2,
∴AC2﹣(AC﹣2)2=102﹣(2)2,
解得:AC=5.
15.【解答】解:(1)∵BD∥AC,AC=6,BD=4,
∴△ACE∽△BDE,
∴,即,
∴,
∵EF∥AC,
∴△BEF∽△BAC,
∴,即,
∴;
(2)由(1)知△BEF∽△BAC,
∴,
∴,
∵△BEF的面积为4,
∴S△BAC=25,
由(1)知,,
∴,即,
∴S△BCE=10,
∴S△CEF=S△BCE﹣S△BEF=10﹣4=6,
∴△CEF的面积为6.
16.【解答】(1)证明:如图,
在矩形ABCD中,OD=OC,AB∥CD,∠BCD=90°,
∴∠2=∠3=∠4,∠3+∠5=90°,
∵DE=BE,
∴∠1=∠2,
又∵BE平分∠DBC,
∴∠1=∠6,
∴∠3=∠6,
∴∠6+∠5=90°,
∴BF⊥AC;
(2)解:与△OBF相似的三角形有△ECF,△BAF理由如下:
∵∠1=∠3,∠EFC=∠BFO,
∴△ECF∽△OBF,
∵DE=BE,
∴∠1=∠2,
又∵∠2=∠4,
∴∠1=∠4,
又∵∠BFA=∠OFB,
∴△BAF∽△OBF;
(3)解:在矩形ABCD中,∠4=∠3=∠2,
∵∠1=∠2,∴∠1=∠4.
又∵∠OFB=∠BFA,
∴△OBF∽△BAF.
∵∠1=∠3,∠OFB=∠EFC,
∴△OBF∽△ECF.
∴,
∴,即3CF=2BF,
∴3(CF+OF)=3CF+9=2BF+9,
∴3OC=2BF+9
∴3OA=2BF+9①,
∵△ABF∽△BOF,
∴,
∴BF2=OF AF,
∴BF2=3(OA+3)②,
联立①②,可得BF=1±(负值舍去),
∴DE=BE=2+1+=3+.
17.【解答】(1)解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵BD=CD,
∴∠C=∠CBD,
∴∠ABD=∠C,
∵∠A=∠A,
∴△ABD∽△ACB,
∴,
而AB=4,CA=6,
则AD=,
则CD=AC﹣AD=6﹣=;
(2)①证明:
由(1)可知,∠ABD=∠C,
∵∠AEF=∠ABC,∠AEF+∠CEF=∠AEC=∠ABC+∠BAG,
∴∠CEF=∠BAG,
∴△ABG∽△ECF;
②解:∵△ABG∽△ECF,
∴,
∵BG=2CF,
∴,
由已知及(1)可知,,△ABD∽△ACB,
∴,
∴,
∴BE=BC﹣CE=3,
过点D作DM∥BC交AE于点M,如图,
∴∠ADM=∠ACE,∠AMD=∠AEC,∠BEG=∠DMG,∠GBE=∠MDG,
∴△ADM∽△ACE,△BEG∽△DMG,
∴,
∴,
∴.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练相似三角形的判定与性质训练
1.如图,在△ABC中,AB=AC,D为BC边上一点,E为AC边上一点,且∠ADE=∠B.
(1)求证:△ABD∽△DCE;
(2)若AC=12,BC=11,CE=2,求BD的长.
2.如图,△ABC中,点D,E,F分别在AB,BC,AC边上DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)设.
①若BC=20,求线段BE的长;
②若△EFC的面积是20,求四边形ADEF的面积.
3.如图,Rt△ABC中,∠B=90°,AB=6,BC=8,D是斜边AC上一个动点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF.
(1)求证:四边形BEDF是矩形;
(2)若四边形BEDF为正方形,求的值.
4.如图,在△ABC中,AB=AC=10cm,BC=16cm,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B.
(1)求证:AB CM=BP PC;
(2)当△PCM为直角三角形时,求线段AP的长度.
5.如图,在△ABC中,点D、E分别在边BC、AC上,连接BE、AD交于点G,点F在线段DC上,且∠EFD+∠ADF=180°,,连接FG.
(1)求证:四边形AGFE是平行四边形;
(2)如果∠BDA=∠BAC,求证:AG=AE.
6.如图,在△ABC中,点D在边AB上,AD=4,BD=5,AC=6,△ABC的角平分线AE交CD于点F.
(1)求证:AC2=AD AB;
(2)求证:△ADF∽△ACE;
(3)若AF=4,求AE的长度.
7.如图,已知AB为⊙O的直径,点C在AB的延长线上,点D,E是⊙O上的两点,连接AD,BD,CD,BE,DE,其中∠E=∠C,CD是⊙O的切线.
(1)求∠C的度数.
(2)求证:△BCD∽△DCA.
(3)若AC=8,求⊙O的半径.
8.如图,点E,F分别在矩形ABCD的边AB,CD上,连接EF,交对角线AC于点G,EF∥AD.
(1)求证:△CFG∽△ABC.
(2)若CF=2,FD=4,AD=3,求CG的长.
9.如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,.
(1)若BC=21,求BF的长;
(2)若△ABC的面积为49,求△CEF的面积.
10.如图,点E是矩形ABCD中AD边上一点,△ABE沿BE折叠为△FBE,点F落在CD上.(1)求证:△CFB∽△DEF;
(2)若,BCcm,求BF的值.
11.正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:△ABM∽△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;
(3)求梯形ABCN的面积最大时,点M的位置.
12.如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E作EF⊥ED交AB于点G、交DA延长线于点F.
(1)求证:△ECD∽△DEF;
(2)若CD=4,求AF的长.
13.已知:如图,在△ABC中,D是BC的中点,AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)求证:AF=DF;
(3)若△FCD的面积为5,BC=10,求DE的长.
14.如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交BE于M,FD、AC的延长线交于点N.
(1)求证:△BFM∽△NFA;
(2)求证:DF2=FM FN;
(3)若AC=BC,DN=12,ME:EN=1:2,求线段AC的长.
15.如图,在△ABC中,点E为AB边上一点,分别过点B,E作BD∥AC,EF∥AC,BD交CE的延长线于点D,EF交BC于点F,且AC=6,BD=4.
(1)求EF的长;
(2)若△BEF的面积为4,求△CEF的面积.
16.如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F.
(1)若BE平分∠CBD,求证:BF⊥AC;
(2)找出图中与△OBF相似的三角形,并说明理由;
(3)若OF=3,EF=2,求DE的长度.
17.如图1,在△ABC中,BD平分∠ABC,BD=CD,AB=4,AC=6.
(1)求CD的长;
(2)如图2,在(1)的条件下,E为BC上的点,作∠AEF=∠ABC交AC于点F,AE、BD相交于点G.
①求证:△ABG∽△ECF;
②若BG=2CF,求.
参考答案
1.【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,
∵∠ADE=∠B,
∴∠BAD=∠CDE,
∴△ABD∽△CDE;
(2)解:∵AB=AC,AC=12,
∴AB=12,
由(1)知,△ABD∽△CDE,
∴=即=,
∴BD=3或8.
2.【解答】(1)证明:由已知条件可知:DE∥AC,EF∥AB,
根据平行线的性质可得:∠BED=∠ECF,∠FEC=∠DBE,
∴△BDE∽△EFC;
(2)解:①∵EF∥AB,
∴,
∴,
∵BC=20.
∴.
②解:∵,
∵△EFC的面积是20,
∴S△BDE=5,
∵EF∥AB,,
∴△ABC∽△EFC,,
∴,
∴S△ABC=45,
∴面积为S△ABC﹣S△EFC﹣S△BDE=45﹣5﹣20=20.
3.【解答】(1)证明:∵DE⊥AB于点E,DF⊥BC于点F,
∴∠BED=∠BFD=90°,
∵∠B=90°,
∴四边形BEDF是矩形;
(2)解:∵四边形BEDF为正方形,
∴DE=DF=BE=BF,
设DE=DF=BE=BF=x,则AE=6﹣x,
∵,
∴,
∴x,
经检验,x是原方程的解,
∴AE,
∴AD,
∵AC,
∴DC=AC﹣AD,
∴.
4.【解答】(1)证明:∵AB=AC=10cm,
∴∠B=∠C,
∵∠APM+∠CPM=∠APC=∠B+∠BAP,∠APM=∠B,
∴∠CPM=∠BAP,
∴△CPM∽△BAP,
∴,
∴AB CM=BP PC;
(2)解:∵∠B=∠C≠90°,
当∠PMC=90°时,如图,
由(1)知△CPM∽△BAP,
∴∠APB=∠PMC=90°,
∵AB=AC,
∴点P为BC中点,
∴BP=CP==8(cm),
∴ap==6(cm);
当∠CPM=90°时,如图,作AD⊥BC于点D,则AD=6cm,
由(1)知△CPM∽△BAP,
∴∠BAP=∠CPM=90°,
∵AB=AC,AD⊥BC,
∴,
∵∠BAP=∠BDA=90°,∠ABP=∠DBA,
∴△ABP∽△DBA,
∴,
∴AP=(cm),
综上可知,线段AP的长度为6cm或.
5.【解答】证明:(1)∵∠EFD+∠ADF=180°,
∴AD∥EF,
∴,
又∵,
∴,
∵∠DBG=∠CBE,
∴△BFG∽△BCE,
∴∠BFG=∠BCE,
∴GF∥AC,
∴四边形AGFE是平行四边形;
(2)由(1)得四边形AGFE是平行四边形,∠BDA=∠BAC,且∠ABD=∠ABC,如图,连接AF交GE于点O,
∴OA=OF,△ABD∽△CBA,
∴,即AB2=BC BD,
∵,即BF2=BC BD,
∴AB=BF,
∴BO⊥AF,
即:AF⊥GE,
∴四边形AGFE是菱形,
∴AG=AE.
6.【解答】(1)证明:∵AD=4,BD=5,
∴AB=AD+BD=4+5=9,
∴AC2=62=36,AB AD=9×4=36,
∴AC2=AD AB;
(2)证明:∵AC2=AD AB,
∴,
又∵∠BAC=∠CAD,
∴△ABC∽△ACD,
∴∠ACB=∠ADC,
∵AE平分∠BAC,
∴∠DAF=∠CAE,
∴△DAF∽△CAE;
(3)解:∵△DAF∽△CAE,
∴,
∵AF=4,
∴AE6.
7.【解答】(1)解:连接OD,如图,
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠ODC=90°,
∵∠BOD=2∠E,∠E=∠C,
∴∠BOD=2∠C,
而∠BOD+∠C=90°,
即2∠C+∠C=90°,
∴∠C=30°;
(2)证明:∵AB为直径,
∴∠ADB=90°,
∵∠ADO+∠ODB=90°,∠BDC+∠ODB=90°,
∴∠ADO=∠BDC,
∵OA=OD,
∴∠ADO=∠A,
∴∠BDC=∠A,
∵∠BCD=∠DCA,
∴△BCD∽△DCA;
(3)解:设⊙O的半径为r,则OA=OD=r,OC=8﹣r,
在Rt△OCD中,∵∠C=30°,
∴OC=2OD,
即8﹣r=2r,
解得r,
即⊙O的半径为.
8.【解答】(1)证明:∵EF∥AD,
∴∠CFG=∠D,
∵四边形ABCD是矩形,
∴∠D=∠B,CD∥AB,
∴∠CFG=∠B,∠FCG=∠BAC,
∴△CFG∽△ABC.
(2)解:∵CF=2,FD=4,AD=3,
∴CD=CF+FD=2+4=6,
∵∠D=90°,
∴CA3,
∵GF∥AD,
∴△CFG∽△CDA,
∴,
∴CGCA3,
∴CG的长是.
9.【解答】解:(1)∵DE∥BC,
∴.
∵EF∥AB,
∴,
∴.
设CF=4k,则BF=3k,则CF=4k.
∵BC=21,
∴3k+4k=21,
解得k=3,
∴BF=3k=9;
(2)由(1),得,
∴.
∵EF∥AB,
∴△ABC∽△EFC.
∵,S△ABC=49,
∴S△CEF=16.
10.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠C=∠D=90°,
∴∠CBF+∠CFB=90°,
∵△ABE沿BE折叠为△FBE,
∴∠EFB=∠A=90°,
∴∠DFE+∠CFB=90°,
∴∠DFE=∠CBF,
∴△CFB∽△DEF;
(2)解:由(1)得:△CFB∽△DEF,
∴,
设CF=k,BF=3k(k>0),
∵BF2﹣CF2=BC2,,
∴,
∴k1=2,k2=﹣2(舍去),
∴BF=3k=6cm.
11.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°,
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,
∴△ABM∽△MCN;
(2)解:∵△ABM∽△MCN,
∴,即,
∴,
∴;
(3)解:,
∵,
∴y有最大值,且当x=2时,y取得最大值,最大值为10,
即当点M运动到BC中点时,梯形ABCN的面积最大,最大值为10.
12.【解答】(1)证明:∵在正方形ABCD中,EF⊥ED,
∴∠FED=∠C=90°,
∵BC∥AD,
∴∠CED=∠FDE,
∴△ECD∽△DEF;
(2)解:∵四边形ABCD是正方形,
∴∠C=90°,AD=BC=CD=4,
∵E为BC的中点,
∴CE=0.5BC=2
在Rt△DCE中,
由勾股定理得:DE2=CE2+DC2=22+42=20,
∵△ECD∽△DEF,
∴CE:DE=DE:DF,
∴2:DE=DE:DF,
2DF=DE2,
解得:DF=10,
∵AD=4,
∴AF=DF﹣AD=10﹣4=6.
13.【解答】(1)证明:在△ABC中,D是BC的中点,AD=AC,DE⊥BC,
∴BD=CD,∠ACB=∠FDC,
∴EB=EC,
∴∠ABC=∠FCD,
∴△ABC∽△FCD;
(2)证明:∵△ABC∽△FCD,
∴,
∵AD=AC,BC=2CD,
∴,
∴AF=DF.
(3)解:△FCD的面积为5,BC=10,如图,作AM⊥BC于M,
∵△ABC∽△FCD,
∴,
∴S△ABC=4S△FCD=20,
∵S△ABCBC AM10 AM,
∴AM=4,
∴DM,BM,
∵DE∥AM,
∴,
∴DE BM=AM BD,
即:,
∴.
14.【解答】(1)证明∵DF⊥AB,AD,BE是△ABC的高,
∴∠BFD=∠AFD=∠AEB=∠ADB=90°,
∴∠FBM=90°﹣∠BAC,∠N=90°﹣∠BAC,
∴∠FBM=∠N,
又∵∠BFD=∠AFD,
∴△BFM∽△NFA;
(2)证明:∵△BFM∽△NFA,
∴,
∴FM FN=FB FA,
∵∠FBD+∠FDB=90°,∠FBD+∠FAD=90°,
∴∠FDB=∠FAD,
∵∠BFD=∠AFD,∠FDB=∠FAD,
∴△BFD∽△DFA,
∴,
∴DF2=FM FN;
(3)解:∵AC=BC,
∴∠BAC=∠ABC,
∵∠ABC+∠FDB=∠BAC+∠N=90°,
∴∠FDB=∠N=∠FBM,
∴△ENM∽△FBM∽△FDB,
∴,
∴FB=2FM,FD=2FB=4FM,
∵DF2=FM FN,
∴(4FM)2=FM (4FM+12),
解得:FM=1或0(舍去),
∴FB=2,FD=4,FN=FD+DN=16,
∵,
∴AF=8,AB=AF+BF=10,
在Rt△BFD中,
BD2,
在Rt△ADB与Rt△ADC中,
AD2=AB2﹣BD2=AC2﹣CD2,
∴AC2﹣(AC﹣2)2=102﹣(2)2,
解得:AC=5.
15.【解答】解:(1)∵BD∥AC,AC=6,BD=4,
∴△ACE∽△BDE,
∴,即,
∴,
∵EF∥AC,
∴△BEF∽△BAC,
∴,即,
∴;
(2)由(1)知△BEF∽△BAC,
∴,
∴,
∵△BEF的面积为4,
∴S△BAC=25,
由(1)知,,
∴,即,
∴S△BCE=10,
∴S△CEF=S△BCE﹣S△BEF=10﹣4=6,
∴△CEF的面积为6.
16.【解答】(1)证明:如图,
在矩形ABCD中,OD=OC,AB∥CD,∠BCD=90°,
∴∠2=∠3=∠4,∠3+∠5=90°,
∵DE=BE,
∴∠1=∠2,
又∵BE平分∠DBC,
∴∠1=∠6,
∴∠3=∠6,
∴∠6+∠5=90°,
∴BF⊥AC;
(2)解:与△OBF相似的三角形有△ECF,△BAF理由如下:
∵∠1=∠3,∠EFC=∠BFO,
∴△ECF∽△OBF,
∵DE=BE,
∴∠1=∠2,
又∵∠2=∠4,
∴∠1=∠4,
又∵∠BFA=∠OFB,
∴△BAF∽△OBF;
(3)解:在矩形ABCD中,∠4=∠3=∠2,
∵∠1=∠2,∴∠1=∠4.
又∵∠OFB=∠BFA,
∴△OBF∽△BAF.
∵∠1=∠3,∠OFB=∠EFC,
∴△OBF∽△ECF.
∴,
∴,即3CF=2BF,
∴3(CF+OF)=3CF+9=2BF+9,
∴3OC=2BF+9
∴3OA=2BF+9①,
∵△ABF∽△BOF,
∴,
∴BF2=OF AF,
∴BF2=3(OA+3)②,
联立①②,可得BF=1±(负值舍去),
∴DE=BE=2+1+=3+.
17.【解答】(1)解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵BD=CD,
∴∠C=∠CBD,
∴∠ABD=∠C,
∵∠A=∠A,
∴△ABD∽△ACB,
∴,
而AB=4,CA=6,
则AD=,
则CD=AC﹣AD=6﹣=;
(2)①证明:
由(1)可知,∠ABD=∠C,
∵∠AEF=∠ABC,∠AEF+∠CEF=∠AEC=∠ABC+∠BAG,
∴∠CEF=∠BAG,
∴△ABG∽△ECF;
②解:∵△ABG∽△ECF,
∴,
∵BG=2CF,
∴,
由已知及(1)可知,,△ABD∽△ACB,
∴,
∴,
∴BE=BC﹣CE=3,
过点D作DM∥BC交AE于点M,如图,
∴∠ADM=∠ACE,∠AMD=∠AEC,∠BEG=∠DMG,∠GBE=∠MDG,
∴△ADM∽△ACE,△BEG∽△DMG,
∴,
∴,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
