第9章 中心对称图形—平行四边形期中选填压轴题训练(含答案)
文档属性
| 名称 | 第9章 中心对称图形—平行四边形期中选填压轴题训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 976.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 15:02:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第9章中心对称图形—平行四边形期中选填压轴题训练苏科版2024—2025学年八年级下册
一、选择题
1.如图,在 ABCD中,AB=4,BC=6,∠B=45°,E是BC边上的动点,连结DE,过点A作AF⊥DE于点F.则DE AF的值是( )
A. B. C.12 D.6
2.如图,在平行四边形ABCD中,AB=6cm,BC=16cm,∠ABC的平分线交AD于点F,点E是BC的中点,点P以每秒1cm的速度从点A出发,沿AD向点F运动;点Q同时以每秒2cm的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当以P、Q、E、F为顶点的四边形是平行四边形时,运动的时间为( )
A.2s B.5s C.2s或 D.5s或
3.如图,在 ABCD中,AC,BD相交于点O,AB=2,BC=2,记AC的长为x,BD的长为y,则下列各式正确的是( )
A.x2+y2=16 B.x2+y2=48 C.x2+y2=32 D.y2﹣x2=32
4.如图,矩形ABCD中,P为对角线AC上一点,过P分别作AB、AD的平行线于矩形边相交,若矩形ABCD的面积为S,则阴影部分的面积可以表示为( )
A.S B.S C. D.S
5.如图,在矩形ABCD中,连结AC,在Rt△ABC和Rt△ADC分别作内接正方形BEFG和PQMN,若正方形BEFG的面积为9,正方形PQMN的面积为8,则的值为( )
A. B. C. D.
6.如图,在正方形ABCD中,AC是对角线,点E在边BC上,EF⊥AE,∠DCF=45°.则的值为( )
A. B.1 C. D.
7.如图,正方形ABCD的边长为9,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交BC于点F,以DE,EF为邻边作矩形DEFG,连接CG,下列结论中不正确的是( )
A.矩形DEFG是正方形 B.∠CEF=∠ADE
C.CG平分∠DCH D.
8.如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,连接CE、CF、EF,AC与EF相交于点G,若BE=AF=1,∠BAD=120°,则S△AGF:S△AGE的值为( )
A.1:2 B.1:3 C.1:4 D.1:9
9.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A、B重合),作ME⊥AC于点E,MF⊥BC于点F,连接EF,则EF的最小值是( )
A.2 B.2.4 C.3 D.4
10.如图,△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AB=4,AC=6,则MD等于( )
A.4 B.3 C.2 D.1
二、填空题
11.如图,正方形ABCD中,点E为边BC的中点,点F在边CD上,且∠BAE=∠EAF,若EC=4,则线段DF的长为 .
12.如图,在正方形ABCD中,AB=4,点E、F分别在边AB、CD上,且BE=DF,将线段EF绕点F顺时针旋转90°得到线段MF,连接AM,则线段AM的最小值为 .
13.如图,已知正方形ABCD的边长为2,另一边长为的正方形EFGH的中心与点A重合,连接CE,设CE的中点为M,连接DM,当正方形EFGH绕点A旋转时,DM的最小值为 .
14.如图,在正方形ABCD的AB边上有一点E,将直角三角形CBE沿直线CE进行折叠,点F是点B的对应点.若AB=10,BE,则点F到AD边的距离是 .
15.如图,在矩形ABCD中,AB=20,BC=12,点M、N分别为CD、AB边上的点,MN过矩形ABCD的对称中心O,且CM=4DM.若点G、H分别在AD、BC边上,且GH、MN将矩形ABCD的面积四等分,则AG的长为 .
16.已知:如图,正方形ABCD的边长为,E点是正方形ABCD的边CD上的一点,AE与对角线BD相交于点F,若EC=EF.则∠EAD的度数是 ;AF的长为 .
17.如图,正方形ABCD与正方形正方形EFGH,满足EF∥AB.正方形ABCD的边长为6,正方形EFGH的对角线.
(Ⅰ)正方形EFGH的边长为 .
(Ⅱ)线段CF的中点为M,DH的中点为N,则线段MN的长为 .
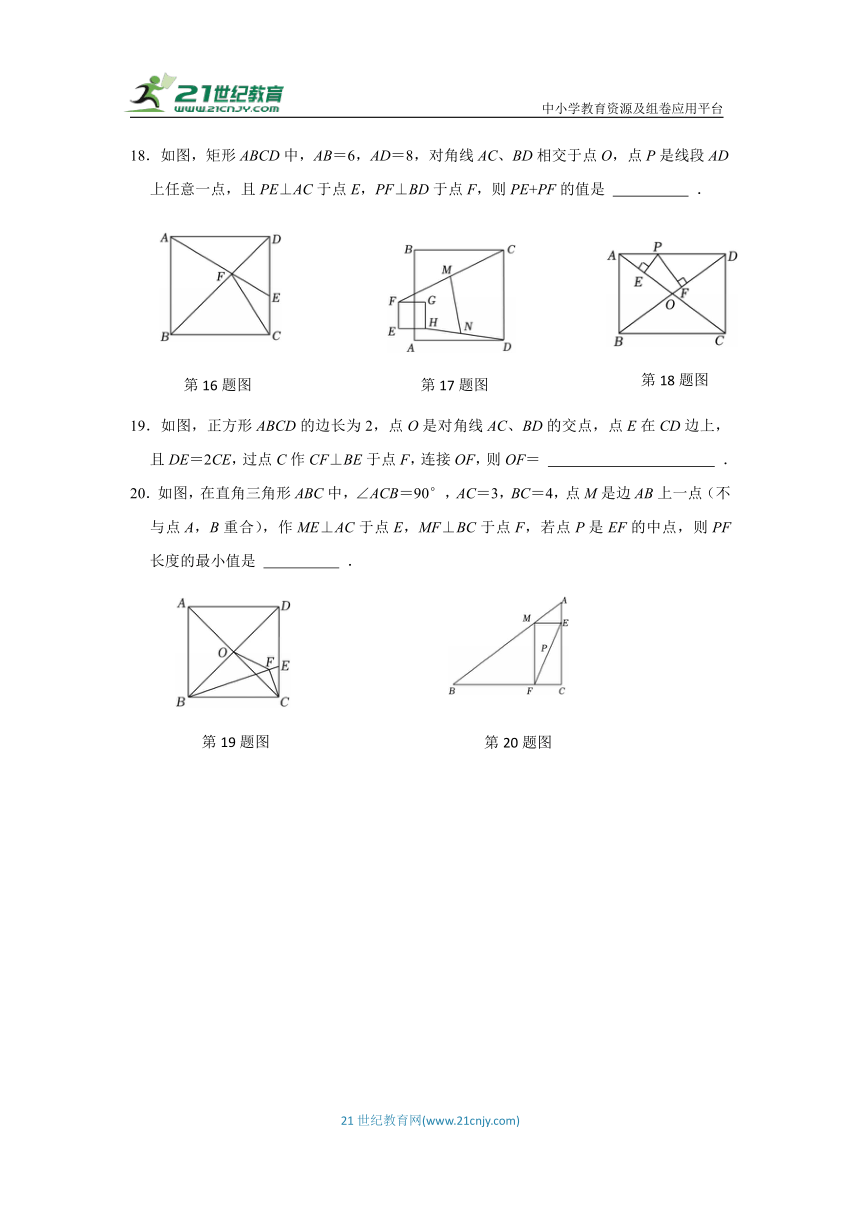
18.如图,矩形ABCD中,AB=6,AD=8,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值是 .
19.如图,正方形ABCD的边长为2,点O是对角线AC、BD的交点,点E在CD边上,且DE=2CE,过点C作CF⊥BE于点F,连接OF,则OF= .
20.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则PF长度的最小值是 .
参考答案
一、选择题
1.【解答】解:过A作AH⊥BC于H,
∵∠B=45°,
∴△ABH是等腰直角三角形,
∴AHAB4=2,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6,
∵AF⊥DE,
∴△EAD的面积AD AHDE AF,
∴DE AF=6×212.
故选:A.
2.【解答】解:∵平行四边形ABCD,BF是∠ABC的平分线,
∴∠AFB=∠CBF=∠ABF,
∴AF=AB=6,
∵点E是BC的中点,
∴,
∴点P运动到F时间为6÷1=6s,点Q运动到E时间为8÷2=4s,
当0≤t<4时,AP=t,CQ=2t,则PF=6﹣t,QE=8﹣2t,
当以P、Q、E、F为顶点的四边形是平行四边形时,PF=QE,
∴6﹣t=8﹣2t,
解得,t=2,
当4≤t<6时,AP=t,CQ=2t,则PF=6﹣t,QE=2t﹣8,
当以P、Q、E、F为顶点的四边形是平行四边形时,PF=QE,
∴6﹣t=2t﹣8,
解得,,
综上所述,当以P、Q、E、F为顶点的四边形是平行四边形时,运动的时间为2s或,
故选:C.
3.【解答】解:作AM⊥BC于点M,DN⊥BC交BC的延长线于点N,则∠ABM=∠N=90°,
∵四边形ABCD是平行四边形,AB=2,BC=2,AC=x,BD=y,
∴AB∥DC,AB=DC,
∴∠ABM=∠DCN,
在△ABM和△DCN中,
,
∴△ABM≌△DCN(AAS),
∴AM=DN,BM=CN,
∴BD2=DN2+BN2=AM2+(BC+CN)2=AM2+(BC+BM)2=AM2+BC2+2BC BM+BM2,
∵AC2=AM2+CM2=AM2+(BC﹣BM)2=AM2+BC2﹣2BC BM+BM2,
∴AC2+BD2=2AM2+2BM2+2BC2=2AB2+2BC2=2×22+2×(2)2=32,
∴x2+y2=32,
故A不符合题意,B不符合题意,C符合题意;
假设y2﹣x2=32成立,则x2+y2=y2﹣x2,
求得x=0,不符合题意,
∴y2﹣x2=32不成立,
故D不符合题意,
故选:C.
4.【解答】解:设AG=a,GD=b,AE=c,EB=d,
在矩形中,有S△ABC=S△ACD,S△AEP=S△AGP,S△CFP=S△CHP,
∴S矩形BHPE=S矩形DGPF,即:ad=bc,
则S矩形ABCD=(a+b)(c+d)=ac+ad+bc+bd,
S空白a(c+d)d(a+b)(ac+ad+ad+bd)(ac+ad+bc+bd)S,
∴S阴影=SSS,
故选:B.
5.【解答】解:在矩形ABCD中,AC为对角线,将矩形分为两个全等的直角三角形Rt△ABC和Rt△ADC.
设AB=a,BC=b,
则,
∵正方形BEFG的面积为9,
∴边长为3,
根据内接正方形公式:,
∴ab=3(a+b).
∵正方形PQMN的面积为8,
∴边长为,
根据内接正方形公式:,
代入,
∵ab=3(a+b),
解得a=b=6,
∴,
∴.
故选:A.
6.【解答】解:在AB上截取BH=BE,连接HE,
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=90°,
∴HEBE,AB﹣BH=BC﹣BE,∠BHE=∠BEH=45°,
∴AH=EC,∠AHE=180°﹣∠BHE=135°,
∵∠DCF=45°,
∴∠ECF=∠ACD+∠DCF=135°,
∴∠AHE=∠ECF,
∵EF⊥AE,
∴∠AEF=90°,
∴∠HAE=∠CEF=90°﹣∠AEB,
在△HAE和△CEF中,
,
∴△HAE≌△CEF(ASA),
∴HE=CF,
∴CFBE,
∴,
故选:C.
7.【解答】解:如图,作EK⊥BC于点K,EL⊥CD于点L,则∠EKF=∠ELD=90°,
∵四边形ABCD是正方形,
∴AB=CB,AD=CD,∠B=∠ADC=90°,
∴∠BCA=∠BAC=45°,∠DCA=∠DAC=45°,
∴∠BCA=∠DCA,
∴EK=EL,
∵∠EKC=∠ELC=∠KCL=90°,
∴四边形EKCL是矩形,
∵四边形DEFG是矩形,
∴∠KEL=∠FED=90,
∴∠FEK=∠DEL=90°﹣∠FEL,
∴△FEK≌△DEL(ASA),
∴DE=FE,
∴矩形DEFG是正方形,故A正确;
∵∠EDG=∠ADC=90°,
∴∠CDG=∠ADE=90°﹣∠CDE,
∵CD=AD,GD=ED,
∴△CDG≌△ADE(SAS),
∴CG=AE,
∴CE+CG=CE+AE=AC,
∵∠B=90°,AB=CB=9,
∴ACAB=9,
∴CE+CG=9,故D正确;
∵△CDG≌△ADE(SAS),
∴∠DAE=∠DCG=45°,
∴CG平分∠DCH,故C正确;
∵∠ADE=∠DEL=∠FEK≠∠CEF,
∴∠CEF≠∠ADE,故B不正确,
故选:B.
8.【解答】解:过点G作GH⊥AD于H,GN⊥AB于N,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=4,∠BAC=∠DAC,
∵BE=AF=1,
∴AE=3,
∵∠BAC=∠DAC,GH⊥AD,GN⊥AB,
∴GN=GH,
∴S△AGF:S△AGEAF×GH:AE×GN=1:3,
故选:B.
9.【解答】解:连接CM,如图,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形EMFC是矩形,
∴EF=MC,
∵∠ACB=90°,AC=3,BC=4,
∴,
当CM⊥AB时,CM取得最小值,即EF取得最小值,
∵,
∴.
∴EF=CM=2.4.
即EF的最小值是2.4.
故选:B.
10.【解答】解:延长BD交AC于H,
在△ADB和△ADH中
,
∴△ADB≌△ADH(ASA)
∴AH=AB=4,BD=DH,
∴HC=AC﹣AH=6﹣4=2,
∵BD=DH,BM=MC,
∴DM是△BCH的中位线,
∴,
故选:D.
11.【解答】解:∵正方形ABCD中,E为BC中点,EC=BE=4,
∴BC=8,
∴正方形边长为8.
过E作EG⊥AF于G.
在△ABE和△AGE中,
,
∴△ABE≌△AGE(AAS),
∴AB=AG=8.
设DF=x,
则CF=8﹣x.
在△EGF和△ECF中,
∴△EGF≌△ECF(HL),
得GF =CF=8﹣x.
∴AF=AG+GF=8+(8﹣x)=16﹣x.
在Rt△ADF中,由勾股定理:AF2=AD2+DF2,
∴(16﹣x)2=82+x2,
解得x=6,
∴线段DF的长为6.
故答案为:6.
12.【解答】解:过M作MH⊥AB交BA延长线于H,交CD延长线于T,过E作EF⊥CD于K,如图:
设BE=DF=x,则CF=AE=4﹣x=DK,
∴KF=DF﹣DK=x﹣(4﹣x)=2x﹣4,
∵将线段EF绕点F顺时针旋转90°得到线段MF,
∴MF=EF,∠MFE=90°,
∴∠KFE=90°﹣∠MFT=∠TMF,
∵∠EKF=90°=∠CTM,
∴△EKF≌△FTM(AAS),
∴EK=TF=4,KF=MT=2x﹣4,
∴MH=MT+TH=2x﹣4+4=2x,AH=DT=TF﹣DF=4﹣x,
∴AM,
∴当x时,AM取最小值;
故答案为:.
13.【解答】解:如图1,在CD的延长线上截取DN=CD,连接EN,
∵点M为CE的中点,
∴DM是△CEN的中位线,
∴DMEN,
由旋转的性质知,点E在以点A为圆心,1为 半径的圆上,
∴当A,E,N三点共线时,且点E在线段AN上时,EN最小,即DM最小,
如图2,
∵DN=CD=2,∠ADN=90°,
∴AN=2,
∴EN=21,
∴DM,
即DM的最小值为,
故答案为:.
14.【解答】解:在正方形ABCD的AB边上有一点E,将直角三角形CBE沿直线CE进行折叠,点F是点B的对应点,AB=10,,如图,连接BF,过F作FH⊥BC于H,
∴AB=BC=CF=10,,BF⊥CE,设垂足为K,
∴BF=2BK,
在直角三角形BCE中,由勾股定理得:,
∴,
∴,
设BH=x,则CH=10﹣x,
∴,
解得:x=2,
在直角三角形BFH中,由勾股定理得:,
∴点F到AD边的距离是10﹣6=4;
故答案为:4.
15.【解答】解:在矩形ABCD中,CD=AB=20,AD=BC=12,
∵CM=4DM,
∴5DM=20,
∴DM=4,
∴CM=CD﹣DM=16,
如图,连接GM、MH、HN、NG,
设AG=x,则DG=12﹣x,
∵点O是矩形ABCD的对称中心,
∴OG=OH,OM=ON,CH=AG=x,
∴四边形MGNH为平行四边形,
∴S△GOM=S△HOM,
∵GH、MN将矩形ABCD的面积四等分,
∴S△GDM=S△MCH,
4×(12﹣x)16 x,
解得:x=2.4,
∴AG=2.4,
故答案为:2.4.
16.【解答】解:∵四边形ABCD是正方形,AC是对角线,
∴AD=CD,∠ADC=90°,
∴,
在△ADF和△CDF中,
,
∴△ADF≌△CDF(SAS),
∴∠DAF=∠DCF,
∵EC=EF,
∴∠ECF=∠EFC,
∴∠AED=2∠ECF,则∠AED=2∠EAD,
在Rt△ADE中,∠EAD+∠AED=90°,
∴∠EAD+2∠EAD=90°,
解得∠EAD=30°;
在Rt△ADE中,,
∴AE=2DE,
由勾股定理得:AE2=AD2+DE2,即,
解得DE=3(负值舍去),
∴AE=6,,
∴;
故答案为:30°;.
17.【解答】解:(Ⅰ)∵正方形EFGH的对角线.
∴EF2,
故答案为:2;
(Ⅱ)连接HM并延长至点P,使MP=MH,作PQ⊥CD于点Q,连接PC、FH、PD,
∵M是线段CF的中点,
∴MF=MC,
在△FHM和△CPM中,
∴△FHM≌△CPM(SAS),
∴FH=PC=2,∠HFM=∠PCM,
∵FG∥BC,
∴∠GFM=∠BCM,
∴∠HFG=∠PCB=45°
∴∠PCQ=45°,
∴PQ=QC=2,
∴DQ=CD+CQ=8,
∴,
∵线段HP的中点为M,DH的中点为N,
∴.
故答案为:.
18.【解答】解:连接OP,过点D作DH⊥AC于点H,如图所示:
∵四边形ABCD为矩形,且AB=6,AD=8,
∴CD=AB=6,OA=OC=OD=OB,∠ADC=90°,
在Rt△ACD中,由勾股定理得:AC10,
∴OA=OC=OD=1/2AC=5,
∵PE⊥AC,PF⊥BD,
∴S△OAPOA PEPE,S△ODPOD PFPF,S△OADOA DHDH,
∵S△OAP+S△ODP=S△OAD,
∴PEPFDH,
∴PE+PF=DH,
∵∠ADC=90°,DH⊥AC,
∴由三角形的面积公式得:S△ACDAC DHAD CD,
∴DH4.8,
∴PE+PF=4.8.
故答案为:4.8.
19.【解答】解:如图,在BE上截取BG=CF,连接OG,
∵Rt△BCE中,CF⊥BE,
∴∠EBC=∠ECF,
∵∠OBC=∠OCD=45°,
∴∠OBG=∠OCF,
在△OBG与△OCF中,
,
∴△OBG≌△OCF(SAS),
∴OG=OF,∠BOG=∠COF,
∴OG⊥OF,
在Rt△BCE中,BC=DC=2,DE=2EC,
∴EC,
∴BE,
∵BC2=BF BE,
∴22=BF,
解得:BF,
∴EF=BE﹣BF,
∵CF2=BF EF,
∴CF,
∴GF=BF﹣BG=BF﹣CF,
在等腰直角△OGF中,OF2GF2,
∴OFGF.
故答案为:.
20.【解答】解:如图,连接MC,
∵∠ACB=90°,ME⊥AC,MF⊥BC,
∴四边形MECF是矩形,
∴MC=EF,
∵∠ACB=90°,AC=3,BC=4,
∴,
∵点P是EF的中点,
∴,
∴CM⊥AB时,CM取得最小值,此时PF取得最小值,
∵,
∴,
∴,
∴PF长度的最小值是1.2.
故答案为:1.2.
21世纪教育网(www.21cnjy.com)
第9章中心对称图形—平行四边形期中选填压轴题训练苏科版2024—2025学年八年级下册
一、选择题
1.如图,在 ABCD中,AB=4,BC=6,∠B=45°,E是BC边上的动点,连结DE,过点A作AF⊥DE于点F.则DE AF的值是( )
A. B. C.12 D.6
2.如图,在平行四边形ABCD中,AB=6cm,BC=16cm,∠ABC的平分线交AD于点F,点E是BC的中点,点P以每秒1cm的速度从点A出发,沿AD向点F运动;点Q同时以每秒2cm的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当以P、Q、E、F为顶点的四边形是平行四边形时,运动的时间为( )
A.2s B.5s C.2s或 D.5s或
3.如图,在 ABCD中,AC,BD相交于点O,AB=2,BC=2,记AC的长为x,BD的长为y,则下列各式正确的是( )
A.x2+y2=16 B.x2+y2=48 C.x2+y2=32 D.y2﹣x2=32
4.如图,矩形ABCD中,P为对角线AC上一点,过P分别作AB、AD的平行线于矩形边相交,若矩形ABCD的面积为S,则阴影部分的面积可以表示为( )
A.S B.S C. D.S
5.如图,在矩形ABCD中,连结AC,在Rt△ABC和Rt△ADC分别作内接正方形BEFG和PQMN,若正方形BEFG的面积为9,正方形PQMN的面积为8,则的值为( )
A. B. C. D.
6.如图,在正方形ABCD中,AC是对角线,点E在边BC上,EF⊥AE,∠DCF=45°.则的值为( )
A. B.1 C. D.
7.如图,正方形ABCD的边长为9,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交BC于点F,以DE,EF为邻边作矩形DEFG,连接CG,下列结论中不正确的是( )
A.矩形DEFG是正方形 B.∠CEF=∠ADE
C.CG平分∠DCH D.
8.如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,连接CE、CF、EF,AC与EF相交于点G,若BE=AF=1,∠BAD=120°,则S△AGF:S△AGE的值为( )
A.1:2 B.1:3 C.1:4 D.1:9
9.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A、B重合),作ME⊥AC于点E,MF⊥BC于点F,连接EF,则EF的最小值是( )
A.2 B.2.4 C.3 D.4
10.如图,△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AB=4,AC=6,则MD等于( )
A.4 B.3 C.2 D.1
二、填空题
11.如图,正方形ABCD中,点E为边BC的中点,点F在边CD上,且∠BAE=∠EAF,若EC=4,则线段DF的长为 .
12.如图,在正方形ABCD中,AB=4,点E、F分别在边AB、CD上,且BE=DF,将线段EF绕点F顺时针旋转90°得到线段MF,连接AM,则线段AM的最小值为 .
13.如图,已知正方形ABCD的边长为2,另一边长为的正方形EFGH的中心与点A重合,连接CE,设CE的中点为M,连接DM,当正方形EFGH绕点A旋转时,DM的最小值为 .
14.如图,在正方形ABCD的AB边上有一点E,将直角三角形CBE沿直线CE进行折叠,点F是点B的对应点.若AB=10,BE,则点F到AD边的距离是 .
15.如图,在矩形ABCD中,AB=20,BC=12,点M、N分别为CD、AB边上的点,MN过矩形ABCD的对称中心O,且CM=4DM.若点G、H分别在AD、BC边上,且GH、MN将矩形ABCD的面积四等分,则AG的长为 .
16.已知:如图,正方形ABCD的边长为,E点是正方形ABCD的边CD上的一点,AE与对角线BD相交于点F,若EC=EF.则∠EAD的度数是 ;AF的长为 .
17.如图,正方形ABCD与正方形正方形EFGH,满足EF∥AB.正方形ABCD的边长为6,正方形EFGH的对角线.
(Ⅰ)正方形EFGH的边长为 .
(Ⅱ)线段CF的中点为M,DH的中点为N,则线段MN的长为 .
18.如图,矩形ABCD中,AB=6,AD=8,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值是 .
19.如图,正方形ABCD的边长为2,点O是对角线AC、BD的交点,点E在CD边上,且DE=2CE,过点C作CF⊥BE于点F,连接OF,则OF= .
20.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则PF长度的最小值是 .
参考答案
一、选择题
1.【解答】解:过A作AH⊥BC于H,
∵∠B=45°,
∴△ABH是等腰直角三角形,
∴AHAB4=2,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6,
∵AF⊥DE,
∴△EAD的面积AD AHDE AF,
∴DE AF=6×212.
故选:A.
2.【解答】解:∵平行四边形ABCD,BF是∠ABC的平分线,
∴∠AFB=∠CBF=∠ABF,
∴AF=AB=6,
∵点E是BC的中点,
∴,
∴点P运动到F时间为6÷1=6s,点Q运动到E时间为8÷2=4s,
当0≤t<4时,AP=t,CQ=2t,则PF=6﹣t,QE=8﹣2t,
当以P、Q、E、F为顶点的四边形是平行四边形时,PF=QE,
∴6﹣t=8﹣2t,
解得,t=2,
当4≤t<6时,AP=t,CQ=2t,则PF=6﹣t,QE=2t﹣8,
当以P、Q、E、F为顶点的四边形是平行四边形时,PF=QE,
∴6﹣t=2t﹣8,
解得,,
综上所述,当以P、Q、E、F为顶点的四边形是平行四边形时,运动的时间为2s或,
故选:C.
3.【解答】解:作AM⊥BC于点M,DN⊥BC交BC的延长线于点N,则∠ABM=∠N=90°,
∵四边形ABCD是平行四边形,AB=2,BC=2,AC=x,BD=y,
∴AB∥DC,AB=DC,
∴∠ABM=∠DCN,
在△ABM和△DCN中,
,
∴△ABM≌△DCN(AAS),
∴AM=DN,BM=CN,
∴BD2=DN2+BN2=AM2+(BC+CN)2=AM2+(BC+BM)2=AM2+BC2+2BC BM+BM2,
∵AC2=AM2+CM2=AM2+(BC﹣BM)2=AM2+BC2﹣2BC BM+BM2,
∴AC2+BD2=2AM2+2BM2+2BC2=2AB2+2BC2=2×22+2×(2)2=32,
∴x2+y2=32,
故A不符合题意,B不符合题意,C符合题意;
假设y2﹣x2=32成立,则x2+y2=y2﹣x2,
求得x=0,不符合题意,
∴y2﹣x2=32不成立,
故D不符合题意,
故选:C.
4.【解答】解:设AG=a,GD=b,AE=c,EB=d,
在矩形中,有S△ABC=S△ACD,S△AEP=S△AGP,S△CFP=S△CHP,
∴S矩形BHPE=S矩形DGPF,即:ad=bc,
则S矩形ABCD=(a+b)(c+d)=ac+ad+bc+bd,
S空白a(c+d)d(a+b)(ac+ad+ad+bd)(ac+ad+bc+bd)S,
∴S阴影=SSS,
故选:B.
5.【解答】解:在矩形ABCD中,AC为对角线,将矩形分为两个全等的直角三角形Rt△ABC和Rt△ADC.
设AB=a,BC=b,
则,
∵正方形BEFG的面积为9,
∴边长为3,
根据内接正方形公式:,
∴ab=3(a+b).
∵正方形PQMN的面积为8,
∴边长为,
根据内接正方形公式:,
代入,
∵ab=3(a+b),
解得a=b=6,
∴,
∴.
故选:A.
6.【解答】解:在AB上截取BH=BE,连接HE,
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=90°,
∴HEBE,AB﹣BH=BC﹣BE,∠BHE=∠BEH=45°,
∴AH=EC,∠AHE=180°﹣∠BHE=135°,
∵∠DCF=45°,
∴∠ECF=∠ACD+∠DCF=135°,
∴∠AHE=∠ECF,
∵EF⊥AE,
∴∠AEF=90°,
∴∠HAE=∠CEF=90°﹣∠AEB,
在△HAE和△CEF中,
,
∴△HAE≌△CEF(ASA),
∴HE=CF,
∴CFBE,
∴,
故选:C.
7.【解答】解:如图,作EK⊥BC于点K,EL⊥CD于点L,则∠EKF=∠ELD=90°,
∵四边形ABCD是正方形,
∴AB=CB,AD=CD,∠B=∠ADC=90°,
∴∠BCA=∠BAC=45°,∠DCA=∠DAC=45°,
∴∠BCA=∠DCA,
∴EK=EL,
∵∠EKC=∠ELC=∠KCL=90°,
∴四边形EKCL是矩形,
∵四边形DEFG是矩形,
∴∠KEL=∠FED=90,
∴∠FEK=∠DEL=90°﹣∠FEL,
∴△FEK≌△DEL(ASA),
∴DE=FE,
∴矩形DEFG是正方形,故A正确;
∵∠EDG=∠ADC=90°,
∴∠CDG=∠ADE=90°﹣∠CDE,
∵CD=AD,GD=ED,
∴△CDG≌△ADE(SAS),
∴CG=AE,
∴CE+CG=CE+AE=AC,
∵∠B=90°,AB=CB=9,
∴ACAB=9,
∴CE+CG=9,故D正确;
∵△CDG≌△ADE(SAS),
∴∠DAE=∠DCG=45°,
∴CG平分∠DCH,故C正确;
∵∠ADE=∠DEL=∠FEK≠∠CEF,
∴∠CEF≠∠ADE,故B不正确,
故选:B.
8.【解答】解:过点G作GH⊥AD于H,GN⊥AB于N,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=4,∠BAC=∠DAC,
∵BE=AF=1,
∴AE=3,
∵∠BAC=∠DAC,GH⊥AD,GN⊥AB,
∴GN=GH,
∴S△AGF:S△AGEAF×GH:AE×GN=1:3,
故选:B.
9.【解答】解:连接CM,如图,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形EMFC是矩形,
∴EF=MC,
∵∠ACB=90°,AC=3,BC=4,
∴,
当CM⊥AB时,CM取得最小值,即EF取得最小值,
∵,
∴.
∴EF=CM=2.4.
即EF的最小值是2.4.
故选:B.
10.【解答】解:延长BD交AC于H,
在△ADB和△ADH中
,
∴△ADB≌△ADH(ASA)
∴AH=AB=4,BD=DH,
∴HC=AC﹣AH=6﹣4=2,
∵BD=DH,BM=MC,
∴DM是△BCH的中位线,
∴,
故选:D.
11.【解答】解:∵正方形ABCD中,E为BC中点,EC=BE=4,
∴BC=8,
∴正方形边长为8.
过E作EG⊥AF于G.
在△ABE和△AGE中,
,
∴△ABE≌△AGE(AAS),
∴AB=AG=8.
设DF=x,
则CF=8﹣x.
在△EGF和△ECF中,
∴△EGF≌△ECF(HL),
得GF =CF=8﹣x.
∴AF=AG+GF=8+(8﹣x)=16﹣x.
在Rt△ADF中,由勾股定理:AF2=AD2+DF2,
∴(16﹣x)2=82+x2,
解得x=6,
∴线段DF的长为6.
故答案为:6.
12.【解答】解:过M作MH⊥AB交BA延长线于H,交CD延长线于T,过E作EF⊥CD于K,如图:
设BE=DF=x,则CF=AE=4﹣x=DK,
∴KF=DF﹣DK=x﹣(4﹣x)=2x﹣4,
∵将线段EF绕点F顺时针旋转90°得到线段MF,
∴MF=EF,∠MFE=90°,
∴∠KFE=90°﹣∠MFT=∠TMF,
∵∠EKF=90°=∠CTM,
∴△EKF≌△FTM(AAS),
∴EK=TF=4,KF=MT=2x﹣4,
∴MH=MT+TH=2x﹣4+4=2x,AH=DT=TF﹣DF=4﹣x,
∴AM,
∴当x时,AM取最小值;
故答案为:.
13.【解答】解:如图1,在CD的延长线上截取DN=CD,连接EN,
∵点M为CE的中点,
∴DM是△CEN的中位线,
∴DMEN,
由旋转的性质知,点E在以点A为圆心,1为 半径的圆上,
∴当A,E,N三点共线时,且点E在线段AN上时,EN最小,即DM最小,
如图2,
∵DN=CD=2,∠ADN=90°,
∴AN=2,
∴EN=21,
∴DM,
即DM的最小值为,
故答案为:.
14.【解答】解:在正方形ABCD的AB边上有一点E,将直角三角形CBE沿直线CE进行折叠,点F是点B的对应点,AB=10,,如图,连接BF,过F作FH⊥BC于H,
∴AB=BC=CF=10,,BF⊥CE,设垂足为K,
∴BF=2BK,
在直角三角形BCE中,由勾股定理得:,
∴,
∴,
设BH=x,则CH=10﹣x,
∴,
解得:x=2,
在直角三角形BFH中,由勾股定理得:,
∴点F到AD边的距离是10﹣6=4;
故答案为:4.
15.【解答】解:在矩形ABCD中,CD=AB=20,AD=BC=12,
∵CM=4DM,
∴5DM=20,
∴DM=4,
∴CM=CD﹣DM=16,
如图,连接GM、MH、HN、NG,
设AG=x,则DG=12﹣x,
∵点O是矩形ABCD的对称中心,
∴OG=OH,OM=ON,CH=AG=x,
∴四边形MGNH为平行四边形,
∴S△GOM=S△HOM,
∵GH、MN将矩形ABCD的面积四等分,
∴S△GDM=S△MCH,
4×(12﹣x)16 x,
解得:x=2.4,
∴AG=2.4,
故答案为:2.4.
16.【解答】解:∵四边形ABCD是正方形,AC是对角线,
∴AD=CD,∠ADC=90°,
∴,
在△ADF和△CDF中,
,
∴△ADF≌△CDF(SAS),
∴∠DAF=∠DCF,
∵EC=EF,
∴∠ECF=∠EFC,
∴∠AED=2∠ECF,则∠AED=2∠EAD,
在Rt△ADE中,∠EAD+∠AED=90°,
∴∠EAD+2∠EAD=90°,
解得∠EAD=30°;
在Rt△ADE中,,
∴AE=2DE,
由勾股定理得:AE2=AD2+DE2,即,
解得DE=3(负值舍去),
∴AE=6,,
∴;
故答案为:30°;.
17.【解答】解:(Ⅰ)∵正方形EFGH的对角线.
∴EF2,
故答案为:2;
(Ⅱ)连接HM并延长至点P,使MP=MH,作PQ⊥CD于点Q,连接PC、FH、PD,
∵M是线段CF的中点,
∴MF=MC,
在△FHM和△CPM中,
∴△FHM≌△CPM(SAS),
∴FH=PC=2,∠HFM=∠PCM,
∵FG∥BC,
∴∠GFM=∠BCM,
∴∠HFG=∠PCB=45°
∴∠PCQ=45°,
∴PQ=QC=2,
∴DQ=CD+CQ=8,
∴,
∵线段HP的中点为M,DH的中点为N,
∴.
故答案为:.
18.【解答】解:连接OP,过点D作DH⊥AC于点H,如图所示:
∵四边形ABCD为矩形,且AB=6,AD=8,
∴CD=AB=6,OA=OC=OD=OB,∠ADC=90°,
在Rt△ACD中,由勾股定理得:AC10,
∴OA=OC=OD=1/2AC=5,
∵PE⊥AC,PF⊥BD,
∴S△OAPOA PEPE,S△ODPOD PFPF,S△OADOA DHDH,
∵S△OAP+S△ODP=S△OAD,
∴PEPFDH,
∴PE+PF=DH,
∵∠ADC=90°,DH⊥AC,
∴由三角形的面积公式得:S△ACDAC DHAD CD,
∴DH4.8,
∴PE+PF=4.8.
故答案为:4.8.
19.【解答】解:如图,在BE上截取BG=CF,连接OG,
∵Rt△BCE中,CF⊥BE,
∴∠EBC=∠ECF,
∵∠OBC=∠OCD=45°,
∴∠OBG=∠OCF,
在△OBG与△OCF中,
,
∴△OBG≌△OCF(SAS),
∴OG=OF,∠BOG=∠COF,
∴OG⊥OF,
在Rt△BCE中,BC=DC=2,DE=2EC,
∴EC,
∴BE,
∵BC2=BF BE,
∴22=BF,
解得:BF,
∴EF=BE﹣BF,
∵CF2=BF EF,
∴CF,
∴GF=BF﹣BG=BF﹣CF,
在等腰直角△OGF中,OF2GF2,
∴OFGF.
故答案为:.
20.【解答】解:如图,连接MC,
∵∠ACB=90°,ME⊥AC,MF⊥BC,
∴四边形MECF是矩形,
∴MC=EF,
∵∠ACB=90°,AC=3,BC=4,
∴,
∵点P是EF的中点,
∴,
∴CM⊥AB时,CM取得最小值,此时PF取得最小值,
∵,
∴,
∴,
∴PF长度的最小值是1.2.
故答案为:1.2.
21世纪教育网(www.21cnjy.com)
同课章节目录
