湘教版2024—2025学年七年级下学期数学期中考试模拟试卷(含答案)
文档属性
| 名称 | 湘教版2024—2025学年七年级下学期数学期中考试模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 406.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 15:05:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版2024—2025学年七年级下学期数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列计算正确的是( )
A.(a3)3=a9 B.a3 a4=a12
C.a2+a3=a5 D.(a2b2)2=a2b4
2.下列各数中,无理数是( )
A. B. C. D.
3.下列说法正确的是( )
A.若a>b,则a﹣2<b﹣2 B.若a>b,则a2>b2
C.若a>b,则ac2>bc2 D.若ac2>bc2,则a>b
4.如图,已知a,b,c,d四条直线,下列不能判断a∥b的是( )
A.∠2=∠3 B.∠4=∠5
C.∠1+∠4=180° D.∠1+∠3=180°
5.下列各式能用平方差公式计算的是( )
A.(a+b)(﹣a﹣b) B.(a+b)(b+a)
C.(a﹣b)(b﹣a) D.(a+b)(a﹣b)
6.已知432=1849,442=1936,452=2025,462=2116.若n为整数,且,则n的值为( )
A.43 B.44 C.45 D.46
7.台灯的光亮照射范围相对比较集中,便于阅读、学习、工作且节省能源.某款稻草人小台灯进价10元,标价15元,商店为了促销,决定打折销售,但每台利润不少于2元,则最多可打几折销售.( )
A.6 B.7 C.8 D.9
8.如图,Rt△ABC的直角顶点A在直线a上,斜边BC在直线b上,若a∥|b,∠1=40°,则∠2=( )
A.50° B.40°
C.30° D.45°
9.已知a=8131,b=2741,c=961,则a,b,c的大小关系是( )
A.a>b>c B.a>c>b C.c>b>a D.b>c>a
10.若关于x的不等式组的解集只有3个整数解,则a的取值范围是( )
A.10<a≤12 B.10≤a<12 C.9≤a<10 D.9<a≤10
二、填空题(6小题,每题3分,共18分)
11.若2m=3,2n=5,则22m+n= .
12.比较大小: .
13.若(m+1)x|m|﹣5>0是关于x的一元一次不等式,则m的值为 .
14.如图:AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为 .
15.若x2﹣(k﹣2)x+9是完全平方式,则k= .
16.若计算(2+x2+mx3)(1﹣5x)的结果不含x3项,那么m的值为 .
第II卷
湘教版2024—2025学年七年级下册数学期中考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算0.
18.计算:
(1)解不等式并把解集在数轴上表示出来:x﹣2(x﹣1)≥1;
(2)解不等式组,并求该不等式组的非负整数解.
19.先化简,再求值:(2+a)(2﹣a)+2a(a﹣3b)﹣(a﹣2b)2,其中a=1,b=2.
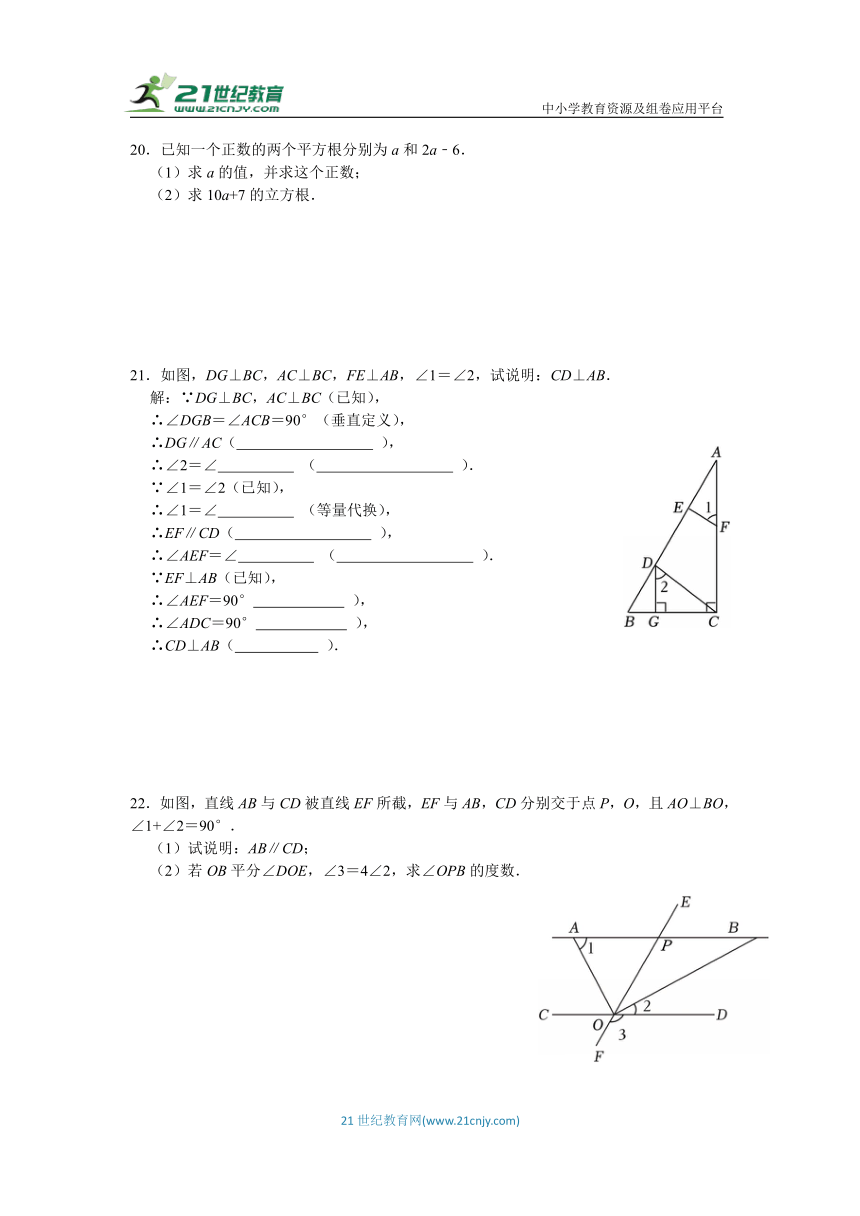
20.已知一个正数的两个平方根分别为a和2a﹣6.
(1)求a的值,并求这个正数;
(2)求10a+7的立方根.
21.如图,DG⊥BC,AC⊥BC,FE⊥AB,∠1=∠2,试说明:CD⊥AB.
解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG∥AC( ),
∴∠2=∠ ( ).
∵∠1=∠2(已知),
∴∠1=∠ (等量代换),
∴EF∥CD( ),
∴∠AEF=∠ ( ).
∵EF⊥AB(已知),
∴∠AEF=90° ),
∴∠ADC=90° ),
∴CD⊥AB( ).
22.如图,直线AB与CD被直线EF所截,EF与AB,CD分别交于点P,O,且AO⊥BO,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若OB平分∠DOE,∠3=4∠2,求∠OPB的度数.
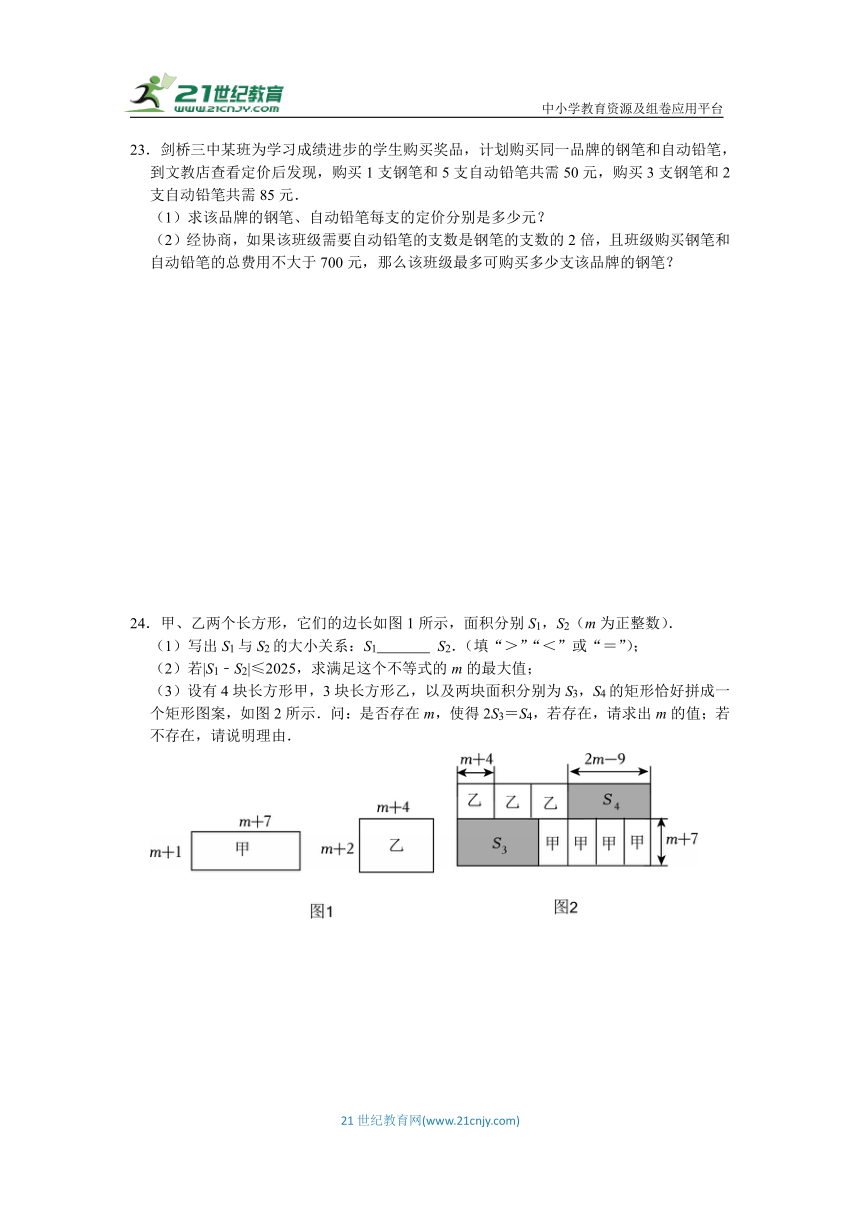
23.剑桥三中某班为学习成绩进步的学生购买奖品,计划购买同一品牌的钢笔和自动铅笔,到文教店查看定价后发现,购买1支钢笔和5支自动铅笔共需50元,购买3支钢笔和2支自动铅笔共需85元.
(1)求该品牌的钢笔、自动铅笔每支的定价分别是多少元?
(2)经协商,如果该班级需要自动铅笔的支数是钢笔的支数的2倍,且班级购买钢笔和自动铅笔的总费用不大于700元,那么该班级最多可购买多少支该品牌的钢笔?
24.甲、乙两个长方形,它们的边长如图1所示,面积分别S1,S2(m为正整数).
(1)写出S1与S2的大小关系:S1 S2.(填“>”“<”或“=”);
(2)若|S1﹣S2|≤2025,求满足这个不等式的m的最大值;
(3)设有4块长方形甲,3块长方形乙,以及两块面积分别为S3,S4的矩形恰好拼成一个矩形图案,如图2所示.问:是否存在m,使得2S3=S4,若存在,请求出m的值;若不存在,请说明理由.
25.已知点B,D分别在AK和CF上,且CF∥AK.
(1)如图1,若∠CDE=110°,∠DEB=120°,则∠ABE的度数为 ;
(2)如图2,DG平分∠FDE,GD延长线与∠ABE的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数.
(3)点E为平面内直线AK与CF中间一点,BM平分∠EBK,DN平分∠CDE,作DP∥BM,在图3中画出图形,并直接写出∠PDN与∠DEB之间的关系.
参考答案
一、选择题
1.【解答】解:A、(a3)3=a9,故此选项符合题意;
B、a3 a4=a7,故此选项不符合题意;
C、a2与a3不是同类项,不能合并,故此选项不符合题意;
D、(a2b2)2=a4b4,故此选项不符合题意;
故选:A.
2.【解答】解:A、是开方开不尽的数,是无理数,符合题意;
B、不是无理数,不符合题意;
C、是无限循环小数,不是无理数,不符合题意;
D、不是无理数,不符合题意,
故选:A.
3.【解答】解:A、若a>b,则a﹣2>b﹣2,计算不正确,不符合题意;
B、当a=﹣1,b=﹣2时,a>b,a2<b2,计算不正确,不符合题意;
C、若a>b,当c≠0时,ac2>bc2,计算不正确,不符合题意;
D.、若ac2>bc2,则a>b,计算正确,符合题意.
故选:D.
4.【解答】解:A.根据同位角相等,两直线平行,由∠2=∠3,能判断直线a∥b;
B.根据内错角相等,两直线平行,由∠4=∠5,能判断直线a∥b;
C.由∠1+∠4=180°,不能判断直线a∥b;
D.由∠1+∠3=180°,∠1+∠2=180°,可得∠2=∠3,根据同位角相等,两直线平行,能判断直线a∥b;
故选:C.
5.【解答】解:A、(a+b)(﹣a﹣b)=﹣(a+b)(a+b)=﹣(a+b)2=﹣a2﹣2ab﹣b2,不能用平方差公式计算,故此选项不符合题意;
B、(a+b)(b+a)=(a+b)(a+b)=(a+b)2=a2+2ab+b2,不能用平方差公式计算,故此选项不符合题意;
C、(a﹣b)(b﹣a)=﹣(a﹣b)(a﹣b)=﹣(a﹣b)2=﹣a2+2ab﹣b2,不能用平方差公式计算,故此选项不符合题意;
D、(a+b)(a﹣b)=a2﹣b2,能用平方差公式计算,故此选项符合题意;
故选:D.
6.【解答】解:∵1936<2014<1025,
∴,
即,
又∵,n为整数,
∴n=44,
故选:B.
7.【解答】解:设打x折,由题意,得:
,
解得:x≥8,
∴最多打8折出售,
故选:C.
8.【解答】解:由平行线性质可知∠1=∠ABC=40°,
∴∠2=50°.
故选:A.
9.【解答】解:因为a=8131=(34)31=3124,
b=2741=(33)41=3123,
c=961=(32)61=3122,
因为124>123>122,
所以a>b>c.
故选:A.
10.【解答】解:,
解不等式①,得x,
解不等式②,得x≥3,
∵关于x的不等式组的解集只有3个整数解,(3个整数解是3,4,5),
∴56,
∴10<a≤12,
故选:A.
二、填空题
11.【解答】解:22m+n=(2m)2 2n=32×5=45.
故答案为:45.
12.【解答】解:∵,,18<12,
∴.
故答案为:>.
13.【解答】解:由条件可知|m|=1且m+1≠0,
∴m=1.
故答案为:1.
14.【解答】解:作DG⊥BC于G,AH⊥BC于H,
∵AD∥BC,∴AH=DG,
又AB∥CD,
∴四边形ABCD是平行四边形,
∴BC=AD=5,又BE=8,
∴CE=3,又△DCE的面积为6,
∴DG=4,
∴四边形ABCD的面积=BC×AH=20,
故答案为:20.
15.【解答】解:由题意得:x2﹣(k﹣2)x+9=(x±3)2,
∴x2﹣(k﹣2)x+9=x2±6x+9,
∴﹣(k﹣2)=±6,
k﹣2=±6,
解得:k=8或﹣4,
故答案为:8或﹣4.
16.【解答】解:∵多项式(2+x2+mx3)(1﹣5x)=﹣5mx4+(m﹣5)x3+x2﹣10x+2不含x3项,
∴m﹣5=0,
解得m=5.
故答案为:5.
三、解答题
17.【解答】解0
=21
.
18.【解答】解:(1)原不等式去括号得:x﹣2x+2≥1,
移项得:﹣x≥1﹣2,
∴x≤1;
在数轴上表示其解集为:
(2)解不等式①得:x≤1,
解不等式②得:x>﹣4,
∴不等式组的解集为:﹣4<x≤1,
∴不等式组的非负整数解为0,1.
19.【解答】解:(2+a)(2﹣a)+2a(a﹣3b)﹣(a﹣2b)2
=4﹣a2+2a2﹣6ab﹣a2+4ab﹣4b2
=4﹣2ab﹣4b2,
当a=1,b=2时,原式=4﹣2×1×2﹣4×22=﹣16.
20.【解答】解:(1)由平方根的性质得,a+2a﹣6=0,
解得a=2,
∴这个正数为22=4;
(2)当a=2时,10a+7=27,
∵27的立方根3,
∴10a+7的立方根为3.
21.【解答】解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG∥AC(同位角相等,两直线平行),
∴∠2=∠ACD(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠1=∠ACD(等量代换),
∴EF∥CD(同位角相等,两直线平行),
∴∠AEF=∠ADC(两直线平行,同位角相等),
∵EF⊥AB(已知),
∴∠AEF=90°(垂直定义),
∴∠ADC=90°(等量代换),
∴CD⊥AB(垂直定义).
故答案为:同位角相等,两直线平行;
ACD;两直线平行,内错角相等;
ACD;
同位角相等,两直线平行;
ADC;两直线平行,同位角相等;
垂直定义;
等量代换;
垂直定义.
22.【解答】解:(1)∵AO⊥BO,
∴∠AOB=90°,
∴∠AOC+∠2=90°,
∵∠1+∠2=90°,
∴∠AOC=∠1,
∴AB∥CD;
(2)∵OB平分∠DOE,
∴∠DOE=2∠2,
∵∠3=4∠2,∠3+∠DOE=180°,
∴4∠2+2∠2=180°,
∴∠2=30°,
∴∠DOE=60°,
∵AB∥CD,
∴∠DOE+∠OPB=180°,
∴∠OPB=120°.
23.【解答】解:(1)设该品牌的钢笔、自动铅笔每支的定价分别是x元、y元,
由题意得:,
解得,
答:该品牌的钢笔、自动铅笔每支的定价分别是25元、5元;
(2)设该班级购买m支该品牌的钢笔,则购买2m支该品牌的自动铅笔,
由题意得:25m+5×2m≤700,
解得:m≤20,
∴该班级最多可购买20支该品牌的钢笔,
答:该班级最多可购买20支该品牌的钢笔.
24.【解答】解:(1)S1=(m+7)(m+1)
=m2+m+7m+7
=m2+8m+7;
S2=(m+4)(m+2)
=m2+2m+4m+8
=m2+6m+8;
,
因为m为正整数,
所以2m﹣1>0,
所以S1>S2.
故答案为:>.
(2)因为S1﹣S2=2m﹣1,|S1﹣S2|≤2025,
即|2m﹣1|≤2025,
2m﹣1≤2025,
2m≤2026,
m≤1013.
所以m得最大值是1013.
(3)S3=[(m+4)×3+2m﹣9﹣(m+1)×4]×(m+7)
=(3m+12+2m﹣9﹣4m﹣4)×(m+7)
=(m﹣1)(m+7)
=m2+7m﹣m﹣7
=m2+6m﹣7;
S4=(2m﹣9)(m+2)
=2m2+4m﹣9m﹣18
=2m2﹣5m﹣18;
因为2S3=S4,
所以2×(m2+6m﹣7)=2m2﹣5m﹣18,
即2m2+12m﹣14=2m2﹣5m﹣18,
17m=﹣4,
,
因为m为正整数,
所以m 不存在.
25.【解答】解:(1)如图1,过点E作EG∥CF,
∴∠CDE+∠DEG=180°,
∵CF∥AK,
∴EG∥AK,
∴∠GEB+∠ABE=180°,
∴∠CDE+∠DEG+∠GEB+∠ABE=360°,
即∠CDE+∠DEB+∠ABE=360°,
∵∠CDE=110°,∠DEB=120°,
∴∠ABE=130°,
故答案为:130°;
(2)如图2,过H点作HM∥CF,过E点作EN∥CF,
∴HM∥CF∥EN∥AK,
∴∠MHD=∠FDG,∠MHB=∠ABH,
∴∠DHB=∠MHB﹣MHD=∠ABH﹣∠FDG,
∵GD平分∠FDE,BH平分∠ABE,
∴∠ABH∠ABE,∠FDG∠FDE,
∴∠DHB∠ABE∠FDE,
即∠ABE﹣∠FDE=2∠DHB,
∵CF∥EN∥AK,
∴∠NEB=180°﹣∠ABE,∠NED=∠FDE,
∴∠NEB+∠NED=180°﹣∠ABE+∠FDE,
即∠BED=180°﹣(∠ABE﹣∠FDE),
∴∠BED=180°﹣2∠DHB,
∵∠BED比∠DHB大60°,
∴∠DHB=∠BED﹣60°,
∴∠BED=180°﹣2(∠BED﹣60°),
∴∠DEB=100°;
(3)∠DEB=180°﹣2∠PDN,理由如下:
①如图3,当点E在B点左侧时,过点E作EG∥CF,
∵CF∥AK,
∴EG∥CF∥AK,
∴∠DEG=∠CDE,∠BEG=180°﹣∠EBK,∠PDF=180°﹣∠DPK,
∵BM平分∠EBK,DN平分∠CDE,
∴∠MBK=∠MBE,∠CDN=∠EDN,
设∠MBK=∠MBE=α,∠CDN=∠EDN=β,
∴∠DEG=∠CDE=2β,∠BEG=180°﹣∠EBK=180°﹣2α,
∴∠DEB=180°+2β﹣2α,
∵DP∥BM,
∴∠DPK=∠MBK=α,
∴∠PDF=180°﹣α,
∴∠PDN=180°﹣∠CDN﹣∠PDF=180°﹣β﹣180°+α=α﹣β,
∴∠DEB=180°+2β﹣2α=180°﹣2(α﹣β)=180°﹣2∠PDN;
②如图4,当点E在B点右侧时,过点E作EG∥CF,
设:∠MBK=∠MBE=α,∠CLN=∠EDN=β,
同理可得:∠DEB=180°+2α﹣2β,∠PDF=180°﹣∠DPB=180°﹣∠MBK=180°﹣α,
∴∠PDN=∠PDF﹣∠EDN﹣∠FDE=180﹣α﹣β﹣(180°﹣2β)=β﹣α,
∴∠DEB=180°+2α﹣2β=180°﹣2(β﹣α)=180°﹣2∠PDN;
综上可得,∠DEB=180°﹣2∠PDN;
故答案为:∠DEB=180°﹣2∠PDN.
21世纪教育网(www.21cnjy.com)
湘教版2024—2025学年七年级下学期数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列计算正确的是( )
A.(a3)3=a9 B.a3 a4=a12
C.a2+a3=a5 D.(a2b2)2=a2b4
2.下列各数中,无理数是( )
A. B. C. D.
3.下列说法正确的是( )
A.若a>b,则a﹣2<b﹣2 B.若a>b,则a2>b2
C.若a>b,则ac2>bc2 D.若ac2>bc2,则a>b
4.如图,已知a,b,c,d四条直线,下列不能判断a∥b的是( )
A.∠2=∠3 B.∠4=∠5
C.∠1+∠4=180° D.∠1+∠3=180°
5.下列各式能用平方差公式计算的是( )
A.(a+b)(﹣a﹣b) B.(a+b)(b+a)
C.(a﹣b)(b﹣a) D.(a+b)(a﹣b)
6.已知432=1849,442=1936,452=2025,462=2116.若n为整数,且,则n的值为( )
A.43 B.44 C.45 D.46
7.台灯的光亮照射范围相对比较集中,便于阅读、学习、工作且节省能源.某款稻草人小台灯进价10元,标价15元,商店为了促销,决定打折销售,但每台利润不少于2元,则最多可打几折销售.( )
A.6 B.7 C.8 D.9
8.如图,Rt△ABC的直角顶点A在直线a上,斜边BC在直线b上,若a∥|b,∠1=40°,则∠2=( )
A.50° B.40°
C.30° D.45°
9.已知a=8131,b=2741,c=961,则a,b,c的大小关系是( )
A.a>b>c B.a>c>b C.c>b>a D.b>c>a
10.若关于x的不等式组的解集只有3个整数解,则a的取值范围是( )
A.10<a≤12 B.10≤a<12 C.9≤a<10 D.9<a≤10
二、填空题(6小题,每题3分,共18分)
11.若2m=3,2n=5,则22m+n= .
12.比较大小: .
13.若(m+1)x|m|﹣5>0是关于x的一元一次不等式,则m的值为 .
14.如图:AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为 .
15.若x2﹣(k﹣2)x+9是完全平方式,则k= .
16.若计算(2+x2+mx3)(1﹣5x)的结果不含x3项,那么m的值为 .
第II卷
湘教版2024—2025学年七年级下册数学期中考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算0.
18.计算:
(1)解不等式并把解集在数轴上表示出来:x﹣2(x﹣1)≥1;
(2)解不等式组,并求该不等式组的非负整数解.
19.先化简,再求值:(2+a)(2﹣a)+2a(a﹣3b)﹣(a﹣2b)2,其中a=1,b=2.
20.已知一个正数的两个平方根分别为a和2a﹣6.
(1)求a的值,并求这个正数;
(2)求10a+7的立方根.
21.如图,DG⊥BC,AC⊥BC,FE⊥AB,∠1=∠2,试说明:CD⊥AB.
解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG∥AC( ),
∴∠2=∠ ( ).
∵∠1=∠2(已知),
∴∠1=∠ (等量代换),
∴EF∥CD( ),
∴∠AEF=∠ ( ).
∵EF⊥AB(已知),
∴∠AEF=90° ),
∴∠ADC=90° ),
∴CD⊥AB( ).
22.如图,直线AB与CD被直线EF所截,EF与AB,CD分别交于点P,O,且AO⊥BO,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若OB平分∠DOE,∠3=4∠2,求∠OPB的度数.
23.剑桥三中某班为学习成绩进步的学生购买奖品,计划购买同一品牌的钢笔和自动铅笔,到文教店查看定价后发现,购买1支钢笔和5支自动铅笔共需50元,购买3支钢笔和2支自动铅笔共需85元.
(1)求该品牌的钢笔、自动铅笔每支的定价分别是多少元?
(2)经协商,如果该班级需要自动铅笔的支数是钢笔的支数的2倍,且班级购买钢笔和自动铅笔的总费用不大于700元,那么该班级最多可购买多少支该品牌的钢笔?
24.甲、乙两个长方形,它们的边长如图1所示,面积分别S1,S2(m为正整数).
(1)写出S1与S2的大小关系:S1 S2.(填“>”“<”或“=”);
(2)若|S1﹣S2|≤2025,求满足这个不等式的m的最大值;
(3)设有4块长方形甲,3块长方形乙,以及两块面积分别为S3,S4的矩形恰好拼成一个矩形图案,如图2所示.问:是否存在m,使得2S3=S4,若存在,请求出m的值;若不存在,请说明理由.
25.已知点B,D分别在AK和CF上,且CF∥AK.
(1)如图1,若∠CDE=110°,∠DEB=120°,则∠ABE的度数为 ;
(2)如图2,DG平分∠FDE,GD延长线与∠ABE的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数.
(3)点E为平面内直线AK与CF中间一点,BM平分∠EBK,DN平分∠CDE,作DP∥BM,在图3中画出图形,并直接写出∠PDN与∠DEB之间的关系.
参考答案
一、选择题
1.【解答】解:A、(a3)3=a9,故此选项符合题意;
B、a3 a4=a7,故此选项不符合题意;
C、a2与a3不是同类项,不能合并,故此选项不符合题意;
D、(a2b2)2=a4b4,故此选项不符合题意;
故选:A.
2.【解答】解:A、是开方开不尽的数,是无理数,符合题意;
B、不是无理数,不符合题意;
C、是无限循环小数,不是无理数,不符合题意;
D、不是无理数,不符合题意,
故选:A.
3.【解答】解:A、若a>b,则a﹣2>b﹣2,计算不正确,不符合题意;
B、当a=﹣1,b=﹣2时,a>b,a2<b2,计算不正确,不符合题意;
C、若a>b,当c≠0时,ac2>bc2,计算不正确,不符合题意;
D.、若ac2>bc2,则a>b,计算正确,符合题意.
故选:D.
4.【解答】解:A.根据同位角相等,两直线平行,由∠2=∠3,能判断直线a∥b;
B.根据内错角相等,两直线平行,由∠4=∠5,能判断直线a∥b;
C.由∠1+∠4=180°,不能判断直线a∥b;
D.由∠1+∠3=180°,∠1+∠2=180°,可得∠2=∠3,根据同位角相等,两直线平行,能判断直线a∥b;
故选:C.
5.【解答】解:A、(a+b)(﹣a﹣b)=﹣(a+b)(a+b)=﹣(a+b)2=﹣a2﹣2ab﹣b2,不能用平方差公式计算,故此选项不符合题意;
B、(a+b)(b+a)=(a+b)(a+b)=(a+b)2=a2+2ab+b2,不能用平方差公式计算,故此选项不符合题意;
C、(a﹣b)(b﹣a)=﹣(a﹣b)(a﹣b)=﹣(a﹣b)2=﹣a2+2ab﹣b2,不能用平方差公式计算,故此选项不符合题意;
D、(a+b)(a﹣b)=a2﹣b2,能用平方差公式计算,故此选项符合题意;
故选:D.
6.【解答】解:∵1936<2014<1025,
∴,
即,
又∵,n为整数,
∴n=44,
故选:B.
7.【解答】解:设打x折,由题意,得:
,
解得:x≥8,
∴最多打8折出售,
故选:C.
8.【解答】解:由平行线性质可知∠1=∠ABC=40°,
∴∠2=50°.
故选:A.
9.【解答】解:因为a=8131=(34)31=3124,
b=2741=(33)41=3123,
c=961=(32)61=3122,
因为124>123>122,
所以a>b>c.
故选:A.
10.【解答】解:,
解不等式①,得x,
解不等式②,得x≥3,
∵关于x的不等式组的解集只有3个整数解,(3个整数解是3,4,5),
∴56,
∴10<a≤12,
故选:A.
二、填空题
11.【解答】解:22m+n=(2m)2 2n=32×5=45.
故答案为:45.
12.【解答】解:∵,,18<12,
∴.
故答案为:>.
13.【解答】解:由条件可知|m|=1且m+1≠0,
∴m=1.
故答案为:1.
14.【解答】解:作DG⊥BC于G,AH⊥BC于H,
∵AD∥BC,∴AH=DG,
又AB∥CD,
∴四边形ABCD是平行四边形,
∴BC=AD=5,又BE=8,
∴CE=3,又△DCE的面积为6,
∴DG=4,
∴四边形ABCD的面积=BC×AH=20,
故答案为:20.
15.【解答】解:由题意得:x2﹣(k﹣2)x+9=(x±3)2,
∴x2﹣(k﹣2)x+9=x2±6x+9,
∴﹣(k﹣2)=±6,
k﹣2=±6,
解得:k=8或﹣4,
故答案为:8或﹣4.
16.【解答】解:∵多项式(2+x2+mx3)(1﹣5x)=﹣5mx4+(m﹣5)x3+x2﹣10x+2不含x3项,
∴m﹣5=0,
解得m=5.
故答案为:5.
三、解答题
17.【解答】解0
=21
.
18.【解答】解:(1)原不等式去括号得:x﹣2x+2≥1,
移项得:﹣x≥1﹣2,
∴x≤1;
在数轴上表示其解集为:
(2)解不等式①得:x≤1,
解不等式②得:x>﹣4,
∴不等式组的解集为:﹣4<x≤1,
∴不等式组的非负整数解为0,1.
19.【解答】解:(2+a)(2﹣a)+2a(a﹣3b)﹣(a﹣2b)2
=4﹣a2+2a2﹣6ab﹣a2+4ab﹣4b2
=4﹣2ab﹣4b2,
当a=1,b=2时,原式=4﹣2×1×2﹣4×22=﹣16.
20.【解答】解:(1)由平方根的性质得,a+2a﹣6=0,
解得a=2,
∴这个正数为22=4;
(2)当a=2时,10a+7=27,
∵27的立方根3,
∴10a+7的立方根为3.
21.【解答】解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG∥AC(同位角相等,两直线平行),
∴∠2=∠ACD(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠1=∠ACD(等量代换),
∴EF∥CD(同位角相等,两直线平行),
∴∠AEF=∠ADC(两直线平行,同位角相等),
∵EF⊥AB(已知),
∴∠AEF=90°(垂直定义),
∴∠ADC=90°(等量代换),
∴CD⊥AB(垂直定义).
故答案为:同位角相等,两直线平行;
ACD;两直线平行,内错角相等;
ACD;
同位角相等,两直线平行;
ADC;两直线平行,同位角相等;
垂直定义;
等量代换;
垂直定义.
22.【解答】解:(1)∵AO⊥BO,
∴∠AOB=90°,
∴∠AOC+∠2=90°,
∵∠1+∠2=90°,
∴∠AOC=∠1,
∴AB∥CD;
(2)∵OB平分∠DOE,
∴∠DOE=2∠2,
∵∠3=4∠2,∠3+∠DOE=180°,
∴4∠2+2∠2=180°,
∴∠2=30°,
∴∠DOE=60°,
∵AB∥CD,
∴∠DOE+∠OPB=180°,
∴∠OPB=120°.
23.【解答】解:(1)设该品牌的钢笔、自动铅笔每支的定价分别是x元、y元,
由题意得:,
解得,
答:该品牌的钢笔、自动铅笔每支的定价分别是25元、5元;
(2)设该班级购买m支该品牌的钢笔,则购买2m支该品牌的自动铅笔,
由题意得:25m+5×2m≤700,
解得:m≤20,
∴该班级最多可购买20支该品牌的钢笔,
答:该班级最多可购买20支该品牌的钢笔.
24.【解答】解:(1)S1=(m+7)(m+1)
=m2+m+7m+7
=m2+8m+7;
S2=(m+4)(m+2)
=m2+2m+4m+8
=m2+6m+8;
,
因为m为正整数,
所以2m﹣1>0,
所以S1>S2.
故答案为:>.
(2)因为S1﹣S2=2m﹣1,|S1﹣S2|≤2025,
即|2m﹣1|≤2025,
2m﹣1≤2025,
2m≤2026,
m≤1013.
所以m得最大值是1013.
(3)S3=[(m+4)×3+2m﹣9﹣(m+1)×4]×(m+7)
=(3m+12+2m﹣9﹣4m﹣4)×(m+7)
=(m﹣1)(m+7)
=m2+7m﹣m﹣7
=m2+6m﹣7;
S4=(2m﹣9)(m+2)
=2m2+4m﹣9m﹣18
=2m2﹣5m﹣18;
因为2S3=S4,
所以2×(m2+6m﹣7)=2m2﹣5m﹣18,
即2m2+12m﹣14=2m2﹣5m﹣18,
17m=﹣4,
,
因为m为正整数,
所以m 不存在.
25.【解答】解:(1)如图1,过点E作EG∥CF,
∴∠CDE+∠DEG=180°,
∵CF∥AK,
∴EG∥AK,
∴∠GEB+∠ABE=180°,
∴∠CDE+∠DEG+∠GEB+∠ABE=360°,
即∠CDE+∠DEB+∠ABE=360°,
∵∠CDE=110°,∠DEB=120°,
∴∠ABE=130°,
故答案为:130°;
(2)如图2,过H点作HM∥CF,过E点作EN∥CF,
∴HM∥CF∥EN∥AK,
∴∠MHD=∠FDG,∠MHB=∠ABH,
∴∠DHB=∠MHB﹣MHD=∠ABH﹣∠FDG,
∵GD平分∠FDE,BH平分∠ABE,
∴∠ABH∠ABE,∠FDG∠FDE,
∴∠DHB∠ABE∠FDE,
即∠ABE﹣∠FDE=2∠DHB,
∵CF∥EN∥AK,
∴∠NEB=180°﹣∠ABE,∠NED=∠FDE,
∴∠NEB+∠NED=180°﹣∠ABE+∠FDE,
即∠BED=180°﹣(∠ABE﹣∠FDE),
∴∠BED=180°﹣2∠DHB,
∵∠BED比∠DHB大60°,
∴∠DHB=∠BED﹣60°,
∴∠BED=180°﹣2(∠BED﹣60°),
∴∠DEB=100°;
(3)∠DEB=180°﹣2∠PDN,理由如下:
①如图3,当点E在B点左侧时,过点E作EG∥CF,
∵CF∥AK,
∴EG∥CF∥AK,
∴∠DEG=∠CDE,∠BEG=180°﹣∠EBK,∠PDF=180°﹣∠DPK,
∵BM平分∠EBK,DN平分∠CDE,
∴∠MBK=∠MBE,∠CDN=∠EDN,
设∠MBK=∠MBE=α,∠CDN=∠EDN=β,
∴∠DEG=∠CDE=2β,∠BEG=180°﹣∠EBK=180°﹣2α,
∴∠DEB=180°+2β﹣2α,
∵DP∥BM,
∴∠DPK=∠MBK=α,
∴∠PDF=180°﹣α,
∴∠PDN=180°﹣∠CDN﹣∠PDF=180°﹣β﹣180°+α=α﹣β,
∴∠DEB=180°+2β﹣2α=180°﹣2(α﹣β)=180°﹣2∠PDN;
②如图4,当点E在B点右侧时,过点E作EG∥CF,
设:∠MBK=∠MBE=α,∠CLN=∠EDN=β,
同理可得:∠DEB=180°+2α﹣2β,∠PDF=180°﹣∠DPB=180°﹣∠MBK=180°﹣α,
∴∠PDN=∠PDF﹣∠EDN﹣∠FDE=180﹣α﹣β﹣(180°﹣2β)=β﹣α,
∴∠DEB=180°+2α﹣2β=180°﹣2(β﹣α)=180°﹣2∠PDN;
综上可得,∠DEB=180°﹣2∠PDN;
故答案为:∠DEB=180°﹣2∠PDN.
21世纪教育网(www.21cnjy.com)
同课章节目录
