2025年九年级中考数学三轮冲刺训练高频考点突破图形变化之旋转专题训练(含答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练高频考点突破图形变化之旋转专题训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 916.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 15:09:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练高频考点突破图形变化之旋转专题训练
一、选择题
1.纹样作为中国传统文化的重要组成部分,是古人智慧与艺术的结晶,反映出不同时期的风俗习惯,早已融入我们的生活.下面纹样的示意图中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
2.如图,在平面直角坐标系中,点B的坐标为(2,0),将△ABO绕着点B逆时针旋转60°,得到△DBC,则点C的坐标是( )
A. B. C.(2,﹣1) D.(1,﹣2)
3.如图,P是等边△ABC外一点,把BP绕点B顺时针旋转60°到BP1,已知∠AP1B=150°,P1A=1,P1C=2,则等边△ABC的边长为( )
A. B. C. D.
4.如图,在Rt△ABC中,已知∠ACB=90°,AC=3,AB=5,现将AB绕点B顺时针旋转90°到BD,连接CD,则△BCD的面积为( )
A.6 B.12 C.8 D.16
5.如图,经过正方形ABCD对称中心O的直线分别交BA的延长线、AD、BC于点E、F、G.已知DC=4,DF=3,则AE的长为( )
A.2 B. C.3 D.4
6.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,点D是直角边AC上的一个动点,连结BD,以BD为边向外作等边△BDE,连结CE,在点D运动的过程中,线段CE的最小值为( )
A. B.1 C. D.2
二、填空题
7.矩形ABCD绕点B旋转得到矩形BEFG,在旋转过程中,FG恰好过点C,过点G作MN平行于AD交AB,CD于M,N.若AB=3,BC=5,则四边形AMND的面积等于 .
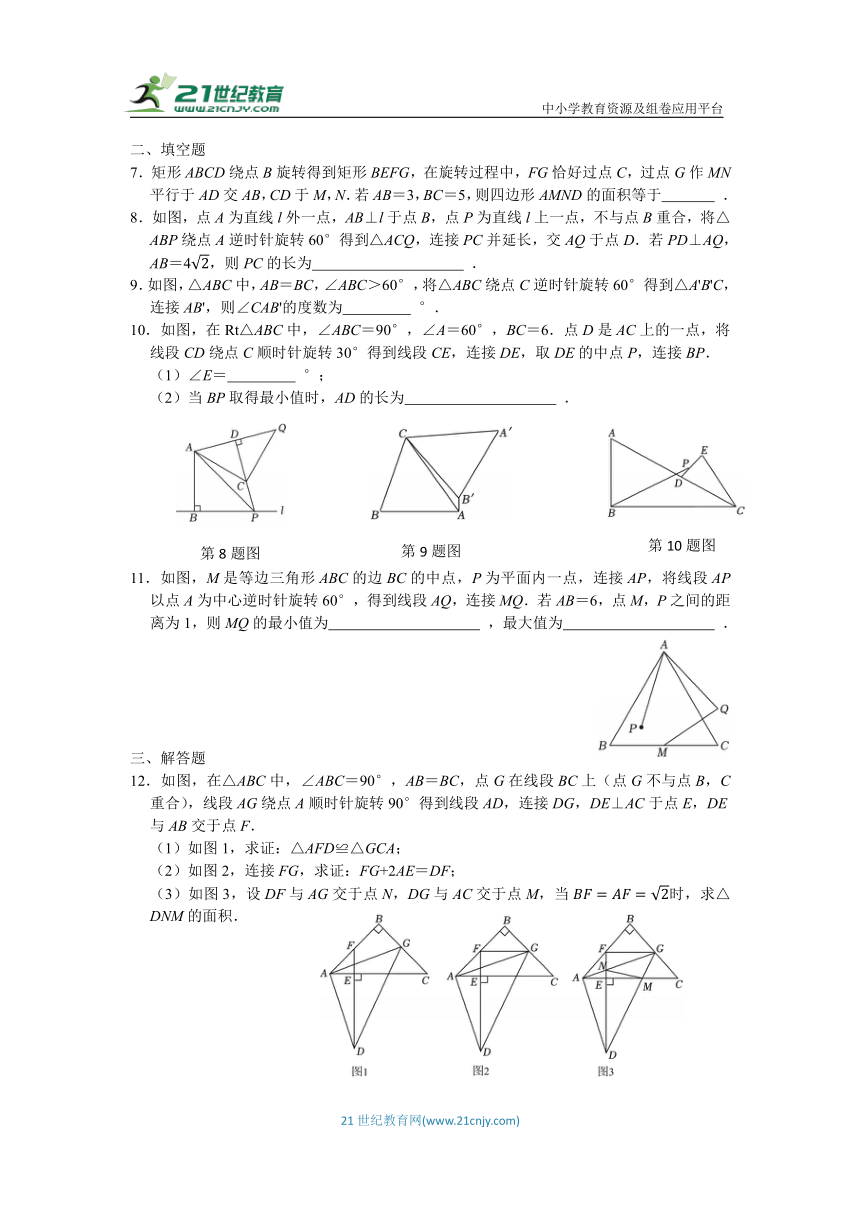
8.如图,点A为直线l外一点,AB⊥l于点B,点P为直线l上一点,不与点B重合,将△ABP绕点A逆时针旋转60°得到△ACQ,连接PC并延长,交AQ于点D.若PD⊥AQ,AB=4,则PC的长为 .
9.如图,△ABC中,AB=BC,∠ABC>60°,将△ABC绕点C逆时针旋转60°得到△A'B'C,连接AB',则∠CAB'的度数为 °.
10.如图,在Rt△ABC中,∠ABC=90°,∠A=60°,BC=6.点D是AC上的一点,将线段CD绕点C顺时针旋转30°得到线段CE,连接DE,取DE的中点P,连接BP.
(1)∠E= °;
(2)当BP取得最小值时,AD的长为 .
11.如图,M是等边三角形ABC的边BC的中点,P为平面内一点,连接AP,将线段AP以点A为中心逆时针旋转60°,得到线段AQ,连接MQ.若AB=6,点M,P之间的距离为1,则MQ的最小值为 ,最大值为 .
三、解答题
12.如图,在△ABC中,∠ABC=90°,AB=BC,点G在线段BC上(点G不与点B,C重合),线段AG绕点A顺时针旋转90°得到线段AD,连接DG,DE⊥AC于点E,DE与AB交于点F.
(1)如图1,求证:△AFD≌△GCA;
(2)如图2,连接FG,求证:FG+2AE=DF;
(3)如图3,设DF与AG交于点N,DG与AC交于点M,当时,求△DNM的面积.
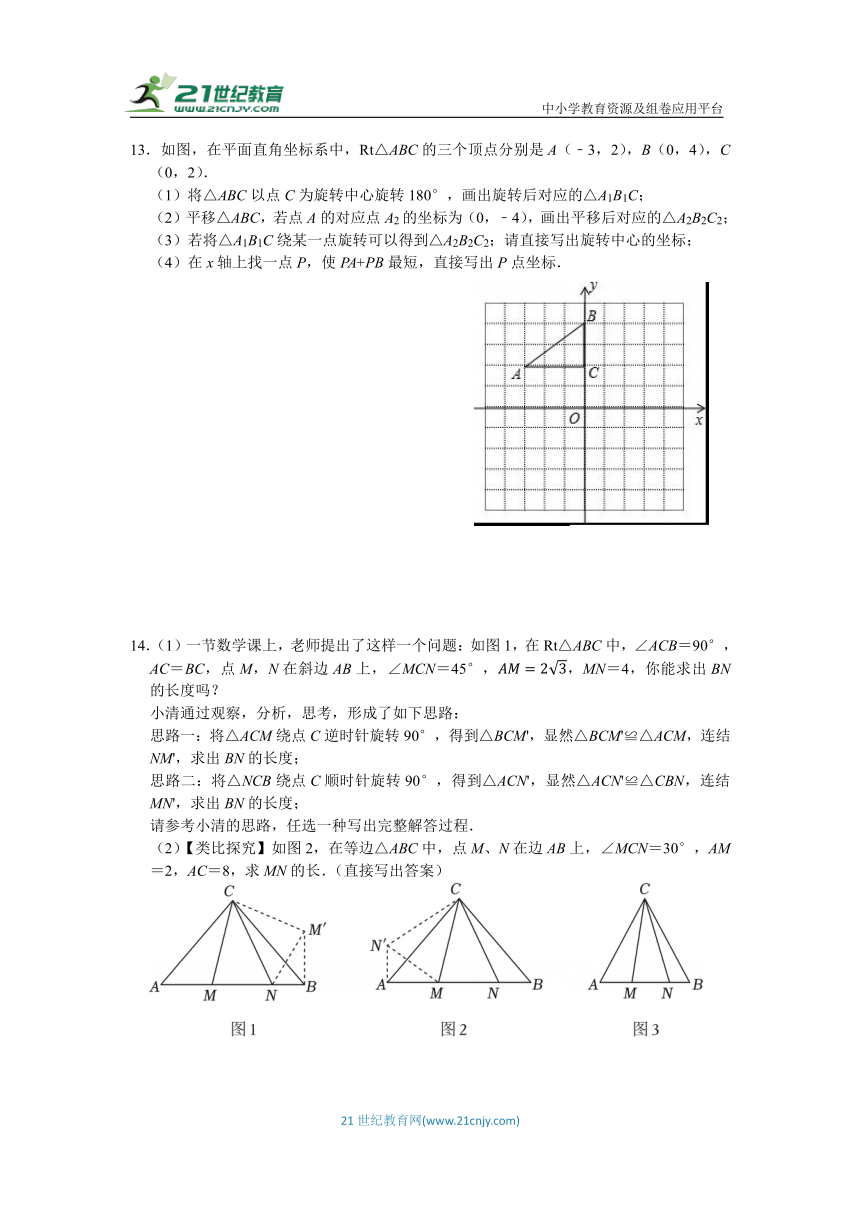
13.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(4)在x轴上找一点P,使PA+PB最短,直接写出P点坐标.
14.(1)一节数学课上,老师提出了这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点M,N在斜边AB上,∠MCN=45°,,MN=4,你能求出BN的长度吗?
小清通过观察,分析,思考,形成了如下思路:
思路一:将△ACM绕点C逆时针旋转90°,得到△BCM',显然△BCM'≌△ACM,连结NM',求出BN的长度;
思路二:将△NCB绕点C顺时针旋转90°,得到△ACN',显然△ACN'≌△CBN,连结MN',求出BN的长度;
请参考小清的思路,任选一种写出完整解答过程.
(2)【类比探究】如图2,在等边△ABC中,点M、N在边AB上,∠MCN=30°,AM=2,AC=8,求MN的长.(直接写出答案)
参考答案
1.【解答】解:A是轴对称图形,但不是中心对称图形,则A不符合题意;
B既不是轴对称图形,也不是中心对称图形,则B不符合题意;
C是轴对称图形,也是中心对称图形,则C不符合题意;
D不是轴对称图形,但它是中心对称图形,则D符合题意;
故选:D.
2.【解答】解:过点C作x轴的垂线,垂足为M,
∵点B坐标为(2,0),
∴OB=2.
由旋转可知,
BC=OB=2,∠OBC=60°.
在Rt△CBM中,
,
则,
∴.
∴,
则OM=2﹣1=1,
∴点C的坐标为.
故选:B.
3.【解答】解:连接AP,PP1,如图,
∵△ABC是等边三角形,
∴AB=AC,∠ABC=60°,
∵BP绕点B顺时针旋转60°到BP1,
∴∠PBP1=60°,BP=BP1,
∴△PBP1为等边三角形,∠ABC﹣∠ABP1=∠PBP1﹣∠ABP1,
即∠P1BC=∠PBA,
在△P1BC和△PBA中,
∴△P1BC≌△PBA(SAS),
∴P1C=AP,
∵P1C=2,
∴AP=P1C=2;
∵△PBP1为等边三角形,
∴BP=PP1=BP1,∠BPP1=∠BP1P=60°,
∵∠AP1B=150°,
∴∠AP1P=∠AP1B﹣∠BP1P=150°﹣60°=90°,
∵∠AP1P=90°,P1A=1,AP=2,
∴,
∴;
取AP的中点D,连接DP1,
则,
∴DP1=AD=AP1,
∴△ADP1为等边三角形,
∴∠DAP1=60°,
∴∠APP1=90°﹣∠DAP1=30°,
∴∠APB=∠APP1+∠BPP1=90°,
∵∠APB=90°,AP=2,,
∴,
∴等边△ABC的边长为.
故选:B.
4.【解答】解:∵Rt△ABC中,∠ACB=90°,AC=3,AB=5,
∴,∠ABC+∠A=180°﹣∠ACB=180°﹣90°=90°,
由旋转知BD=AB=5,∠ABD=90°,
∴∠DBC+∠ABC=90°,
∴∠DBC=∠A,
如图,作DE⊥BC于点E,
在△DEB和△BCA中,
,
∴△DEB≌△BCA(AAS),
∴DE=BC=4,
∴,
所以△BCD的面积为8.
故选:C.
5.【解答】解:过点O作OH⊥AD于点H,连接OD,
∵四边形ABCD是正方形,
∴∠BAD=∠EAF=90°,AD=CD=4,
∵点O是正方形ABCD的中心,
∴AH=DHAD=2,∠ODH=45°,
∵∠OHD=90°,
∴∠ODH=∠HOD=45°,
∴OH=HD=2,
∵DF=3,
∴FH=AF=1,
∵∠EAF=∠OHF=90°,∠AFE=∠OFH,
∴△EAF≌△OHF(ASA),
∴AE=OH=2,
故选:A.
6.【解答】解:延长BC到点F,使FC=BC,连结AF,FE,
∵∠ACB=90°,∠BAC=30°,AB=4,
∴FC=BCAB=2,∠ABF=90°﹣∠BAC=60°,
∴FB=2BC=4,
∴FB=AB,
∴△ABF是等边三角形,
∴∠AFB=60°,
∵△BDE是等边三角形,
∴EB=DB,∠DBE=60°,
∴∠FBE=∠ABD=60°﹣∠DBF,
在△FBE和△ABD中,
,
∴△FBE≌△ABD(SAS),
∴∠BFE=∠BAD=30°,
∴∠AFE=∠AFB+∠BFE=90°,
∴点E在经过点F且与AF垂直的射线FE上运动,
作CH⊥FE交射线FE于点H,则∠CHF=90°,
∴CHFC=1,
∵CE≥CH,
∴CE≥1,
∴CE的最小值为1,
故选:B.
二、填空题
7.【解答】解:∵四边形ABCD为矩形,
∴AB∥CD,AB=CD=3,AD=BC=5,∠A=∠ABC=90°.
由旋转得,BG=AB=3,∠BGC=∠A=90°,
∴CG4,
∴△BCG的面积为6.
∵MN∥AD,AB∥CD,
∴四边形BCNM为平行四边形,
∵∠ABC=90°,
∴四边形BCNM为矩形.
连接BN,
∵S△BCG=S△BCN=6,
∴S矩形BCNM=2S△BCN=12.
∴四边形AMND的面积为S矩形ABCD﹣S矩形BCNM=3×5﹣12=3.
故答案为:3.
8.【解答】解:连接PQ,
∵AB⊥l于点B,点P为直线l上一点,
∴∠ABP=90°,
∵将△ABP绕点A逆时针旋转60°得到△ACQ,
∴∠ACQ=∠ABP=90°,∠PAQ=60°,AQ=AP,AC=AB=4,
∴△APQ是等边三角形,
∵连接PC并延长,交AQ于点D,且PD⊥AQ,
∴PD垂直平分AQ,
∴AC=QC,AD=QD,
∴AQAC48,
∴AQ=AP=8,CD=ADAQ=4,
∴PD4,
∴PC=PD=CD,
故答案为:.
9.【解答】解:如图,连接AA',
∵将△ABC绕点C逆时针旋转60°得到△A'B'C,AB=BC,
∴AC=A'C,A'B'=AB=BC=B'C,∠ACA'=60°,
∴△ACA'是等边三角形,
∴AC=AA',∠CAA‘=60°,
又∵AB'=AB',
∴△AB'C≌△AB'A'(SSS),
∴∠CAB'=∠B'AA'=30°,
故答案为:30.
10.【解答】解:(1)∵将线段CD绕点C顺时针旋转30°得到线段CE,
∴CE=CD,∠DCE=30°,
∴∠E=∠CDE(180°﹣∠DCE)=75°,
故答案为:75.
(2)连接并且延长CP,作BL⊥CP交CP的延长线于点L,交AC于点F,则∠L=90°,
∵CE=CD,∠DCE=30°,P为DE的中点,
∴CP⊥DE,∠DCP=∠ECP∠DCE=15°,
∴PD∥LF,
∵∠ABC=90°,∠A=60°,BC=6,
∴∠ACB=90°﹣∠A=30°,
∴∠LCB=∠ACB+∠DCP=45°,
∴∠LBC=∠LCB=45°,
∴∠ABF=∠ABC﹣∠LBC=45°,
作FH⊥AB于点H,则∠AHF=∠BHF=90°,
∵tan45°=1,tan60°,cos60°,
∴BH=FHAH,AF=2AH,
∵tan60°,
∴ABBC6=2,
∴AH+AH=2,
∴AH=3,
∴AF=2AH=6﹣2,
∵BP≥BL,
∴当点P与点L重合时,BP=BL,此时BP的值最小,
∵点点P与点L重合时,点D与点F重合,
∴AD=AF=6﹣2,
∴当BP取得最小值时,AD的长为6﹣2,
故答案为:6﹣2.
11.【解答】解:如图所示,连接AM,将AM绕点A逆时针旋转60°得到AE,连接PM,ME,QE,
∵,
∴,
∵AM=AE,AP=AQ,∠PAQ=∠MAE=60°,
∴△AME是等边三角形,
∴,
∵∠PAQ﹣∠MAQ=∠MAE﹣∠MAQ,
∴∠PAM=∠QAE,
∴△PAM≌△QAE(SAS),
∴QE=PM=1,
∴点Q在以点E 为圆心、1 为半径的圆上运动,
如图,
∴当点Q在线段ME上时,MQ的值最小,最小值为,当点Q在射线ME上时,MQ有最大值,最大值为,
故答案为:,.
三、解答题
12.【解答】(1)证明:∵线段AD是由AG旋转90°得到的,
∴△DAG是等腰直角三角形,
∴∠DAG=90°,DA=AG.
∵DE⊥AC,
∴∠AED=∠AEF=90°,
∴∠ADE+∠DAE=90°.
∵∠DAE+∠GAC=90°,
∴∠ADE=∠GAC.
∵∠ABC=90°,AB=BC,
∴∠C=∠BAC=45°,
∴∠AFE=∠C=45°,
∴△AFD≌△GCA(AAS).
(2)证明:如图,过点AH⊥AF,交DF于点H,则∠FAH=90°.
∵AE⊥FM,
∴△AEF和△AEH都是等腰直角三角形,
∴AE=EF=EH,
∴FH=EF+EH=2AE.
∵∠DAG=∠FAH=90°,
∴∠DAG﹣∠GAH=∠FAH﹣∠GAH,即∠DAH=∠FAG.
∵DA=AG,
∴△DAH≌△GAF(SAS).
∴DH=FG,
∴DF=DH+FH=FG+2AE.
(3)解:由(1)可知△AFD≌△GCA,
∴AF=CG,
∴△BFG是等腰直角三角形.
∵BF=AF,
∴FGBF=2,AE=EFAF=1.
由(1)可知DF=FG+2AE,
∴DF=2+2×1=4.
∵∠GFE=∠AEF=90°,∠FNG=∠ENA,
∴△FNG∽△ENA,
∴,
∴FN=2EN.
∵EF=FN+EN=1,
∴3EN=1,
∴EN,FN.
∵DE=DF﹣EF=4﹣1=3,
∴DN=EN+DE.
∵EM∥FG,
∴△DEM∽△DFG,
∴,即,
解得EM,
∴DN EM,
∴△DNM的面积为.
13.【解答】解:(1)如图,△A1B1C即为所求;
(2)如图,△A2B2C2即为所求;
(3)将△A1B1C绕某一点旋转可以得到△A2B2C2,旋转中心Q的坐标(1.5,﹣1);
(4)如图,点P即为所求,P点坐标(﹣2,0).
14.【解答】解:(1)思路一:将△ACM绕点C逆时针旋转90°,得到△BCM',连接M'N,
∴△BCM'≌△ACM,
∴BM'=AM,∠BCM'=∠ACM,∠A=∠CBM'=45°,
∴∠ABM'=90°,
∴BN2+BM'2=M'N2,
∵∠MCN=45°,∠ACB=90°,
∴∠M'CB+∠BCN=∠ACM+∠BCN=∠ACB﹣∠MCN=45°,
∵CM'=CM,CN=CN,
∴△NCM≌△NCM'(SAS),
∴MN=M'N,
∴AM2+BN2=MN2,
当AM=2,MN=4时,
∴(2)2+BN2=42,
∴BN=2,
思路二:将△BCN绕点C顺时针旋转90°,得△ACN',连接MN',
∴BN=AN',∠CAN'=∠CBA=45°,∠ACN'=∠BCN,
∴∠N'AB=90°,
∴AN'2+AM2=MN'2,
∵∠MCN=45°,
∴∠ACM+∠BCN=∠ACM+∠ACN'=45°,
∴∠MCN=∠MCN',
∵CN'=CN,CM=CM,
∴△NCM≌△N'CM(SAS),
∴MN=MN',
∴AM2+BN2=MN2,
当AM=2,MN=4时,
∴(2)2+BN2=42,
∴BN=2,
(2)将△ACM绕点C逆时针旋转60°,得到△BCG,连接GN,
∴△BCG≌△ACM,
∴BG=AM,∠BCG=∠ACM,∠A=∠CBG=60°,
∴∠ABG=120°,
同(1)可知△NCM≌△NCG(SAS),
∴MN=GN,
过点G作GH⊥AB于点H,则∠NHG=90°,∠GBH=60°,
设BN=x,
∴MN=AB﹣AM﹣NB=6﹣x,
∵AM=BG=2,
∴BH=1,GH,
∵NH2+GH2=NG2,
∴,
解得x,
∴MN=6.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练高频考点突破图形变化之旋转专题训练
一、选择题
1.纹样作为中国传统文化的重要组成部分,是古人智慧与艺术的结晶,反映出不同时期的风俗习惯,早已融入我们的生活.下面纹样的示意图中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
2.如图,在平面直角坐标系中,点B的坐标为(2,0),将△ABO绕着点B逆时针旋转60°,得到△DBC,则点C的坐标是( )
A. B. C.(2,﹣1) D.(1,﹣2)
3.如图,P是等边△ABC外一点,把BP绕点B顺时针旋转60°到BP1,已知∠AP1B=150°,P1A=1,P1C=2,则等边△ABC的边长为( )
A. B. C. D.
4.如图,在Rt△ABC中,已知∠ACB=90°,AC=3,AB=5,现将AB绕点B顺时针旋转90°到BD,连接CD,则△BCD的面积为( )
A.6 B.12 C.8 D.16
5.如图,经过正方形ABCD对称中心O的直线分别交BA的延长线、AD、BC于点E、F、G.已知DC=4,DF=3,则AE的长为( )
A.2 B. C.3 D.4
6.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,点D是直角边AC上的一个动点,连结BD,以BD为边向外作等边△BDE,连结CE,在点D运动的过程中,线段CE的最小值为( )
A. B.1 C. D.2
二、填空题
7.矩形ABCD绕点B旋转得到矩形BEFG,在旋转过程中,FG恰好过点C,过点G作MN平行于AD交AB,CD于M,N.若AB=3,BC=5,则四边形AMND的面积等于 .
8.如图,点A为直线l外一点,AB⊥l于点B,点P为直线l上一点,不与点B重合,将△ABP绕点A逆时针旋转60°得到△ACQ,连接PC并延长,交AQ于点D.若PD⊥AQ,AB=4,则PC的长为 .
9.如图,△ABC中,AB=BC,∠ABC>60°,将△ABC绕点C逆时针旋转60°得到△A'B'C,连接AB',则∠CAB'的度数为 °.
10.如图,在Rt△ABC中,∠ABC=90°,∠A=60°,BC=6.点D是AC上的一点,将线段CD绕点C顺时针旋转30°得到线段CE,连接DE,取DE的中点P,连接BP.
(1)∠E= °;
(2)当BP取得最小值时,AD的长为 .
11.如图,M是等边三角形ABC的边BC的中点,P为平面内一点,连接AP,将线段AP以点A为中心逆时针旋转60°,得到线段AQ,连接MQ.若AB=6,点M,P之间的距离为1,则MQ的最小值为 ,最大值为 .
三、解答题
12.如图,在△ABC中,∠ABC=90°,AB=BC,点G在线段BC上(点G不与点B,C重合),线段AG绕点A顺时针旋转90°得到线段AD,连接DG,DE⊥AC于点E,DE与AB交于点F.
(1)如图1,求证:△AFD≌△GCA;
(2)如图2,连接FG,求证:FG+2AE=DF;
(3)如图3,设DF与AG交于点N,DG与AC交于点M,当时,求△DNM的面积.
13.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(4)在x轴上找一点P,使PA+PB最短,直接写出P点坐标.
14.(1)一节数学课上,老师提出了这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点M,N在斜边AB上,∠MCN=45°,,MN=4,你能求出BN的长度吗?
小清通过观察,分析,思考,形成了如下思路:
思路一:将△ACM绕点C逆时针旋转90°,得到△BCM',显然△BCM'≌△ACM,连结NM',求出BN的长度;
思路二:将△NCB绕点C顺时针旋转90°,得到△ACN',显然△ACN'≌△CBN,连结MN',求出BN的长度;
请参考小清的思路,任选一种写出完整解答过程.
(2)【类比探究】如图2,在等边△ABC中,点M、N在边AB上,∠MCN=30°,AM=2,AC=8,求MN的长.(直接写出答案)
参考答案
1.【解答】解:A是轴对称图形,但不是中心对称图形,则A不符合题意;
B既不是轴对称图形,也不是中心对称图形,则B不符合题意;
C是轴对称图形,也是中心对称图形,则C不符合题意;
D不是轴对称图形,但它是中心对称图形,则D符合题意;
故选:D.
2.【解答】解:过点C作x轴的垂线,垂足为M,
∵点B坐标为(2,0),
∴OB=2.
由旋转可知,
BC=OB=2,∠OBC=60°.
在Rt△CBM中,
,
则,
∴.
∴,
则OM=2﹣1=1,
∴点C的坐标为.
故选:B.
3.【解答】解:连接AP,PP1,如图,
∵△ABC是等边三角形,
∴AB=AC,∠ABC=60°,
∵BP绕点B顺时针旋转60°到BP1,
∴∠PBP1=60°,BP=BP1,
∴△PBP1为等边三角形,∠ABC﹣∠ABP1=∠PBP1﹣∠ABP1,
即∠P1BC=∠PBA,
在△P1BC和△PBA中,
∴△P1BC≌△PBA(SAS),
∴P1C=AP,
∵P1C=2,
∴AP=P1C=2;
∵△PBP1为等边三角形,
∴BP=PP1=BP1,∠BPP1=∠BP1P=60°,
∵∠AP1B=150°,
∴∠AP1P=∠AP1B﹣∠BP1P=150°﹣60°=90°,
∵∠AP1P=90°,P1A=1,AP=2,
∴,
∴;
取AP的中点D,连接DP1,
则,
∴DP1=AD=AP1,
∴△ADP1为等边三角形,
∴∠DAP1=60°,
∴∠APP1=90°﹣∠DAP1=30°,
∴∠APB=∠APP1+∠BPP1=90°,
∵∠APB=90°,AP=2,,
∴,
∴等边△ABC的边长为.
故选:B.
4.【解答】解:∵Rt△ABC中,∠ACB=90°,AC=3,AB=5,
∴,∠ABC+∠A=180°﹣∠ACB=180°﹣90°=90°,
由旋转知BD=AB=5,∠ABD=90°,
∴∠DBC+∠ABC=90°,
∴∠DBC=∠A,
如图,作DE⊥BC于点E,
在△DEB和△BCA中,
,
∴△DEB≌△BCA(AAS),
∴DE=BC=4,
∴,
所以△BCD的面积为8.
故选:C.
5.【解答】解:过点O作OH⊥AD于点H,连接OD,
∵四边形ABCD是正方形,
∴∠BAD=∠EAF=90°,AD=CD=4,
∵点O是正方形ABCD的中心,
∴AH=DHAD=2,∠ODH=45°,
∵∠OHD=90°,
∴∠ODH=∠HOD=45°,
∴OH=HD=2,
∵DF=3,
∴FH=AF=1,
∵∠EAF=∠OHF=90°,∠AFE=∠OFH,
∴△EAF≌△OHF(ASA),
∴AE=OH=2,
故选:A.
6.【解答】解:延长BC到点F,使FC=BC,连结AF,FE,
∵∠ACB=90°,∠BAC=30°,AB=4,
∴FC=BCAB=2,∠ABF=90°﹣∠BAC=60°,
∴FB=2BC=4,
∴FB=AB,
∴△ABF是等边三角形,
∴∠AFB=60°,
∵△BDE是等边三角形,
∴EB=DB,∠DBE=60°,
∴∠FBE=∠ABD=60°﹣∠DBF,
在△FBE和△ABD中,
,
∴△FBE≌△ABD(SAS),
∴∠BFE=∠BAD=30°,
∴∠AFE=∠AFB+∠BFE=90°,
∴点E在经过点F且与AF垂直的射线FE上运动,
作CH⊥FE交射线FE于点H,则∠CHF=90°,
∴CHFC=1,
∵CE≥CH,
∴CE≥1,
∴CE的最小值为1,
故选:B.
二、填空题
7.【解答】解:∵四边形ABCD为矩形,
∴AB∥CD,AB=CD=3,AD=BC=5,∠A=∠ABC=90°.
由旋转得,BG=AB=3,∠BGC=∠A=90°,
∴CG4,
∴△BCG的面积为6.
∵MN∥AD,AB∥CD,
∴四边形BCNM为平行四边形,
∵∠ABC=90°,
∴四边形BCNM为矩形.
连接BN,
∵S△BCG=S△BCN=6,
∴S矩形BCNM=2S△BCN=12.
∴四边形AMND的面积为S矩形ABCD﹣S矩形BCNM=3×5﹣12=3.
故答案为:3.
8.【解答】解:连接PQ,
∵AB⊥l于点B,点P为直线l上一点,
∴∠ABP=90°,
∵将△ABP绕点A逆时针旋转60°得到△ACQ,
∴∠ACQ=∠ABP=90°,∠PAQ=60°,AQ=AP,AC=AB=4,
∴△APQ是等边三角形,
∵连接PC并延长,交AQ于点D,且PD⊥AQ,
∴PD垂直平分AQ,
∴AC=QC,AD=QD,
∴AQAC48,
∴AQ=AP=8,CD=ADAQ=4,
∴PD4,
∴PC=PD=CD,
故答案为:.
9.【解答】解:如图,连接AA',
∵将△ABC绕点C逆时针旋转60°得到△A'B'C,AB=BC,
∴AC=A'C,A'B'=AB=BC=B'C,∠ACA'=60°,
∴△ACA'是等边三角形,
∴AC=AA',∠CAA‘=60°,
又∵AB'=AB',
∴△AB'C≌△AB'A'(SSS),
∴∠CAB'=∠B'AA'=30°,
故答案为:30.
10.【解答】解:(1)∵将线段CD绕点C顺时针旋转30°得到线段CE,
∴CE=CD,∠DCE=30°,
∴∠E=∠CDE(180°﹣∠DCE)=75°,
故答案为:75.
(2)连接并且延长CP,作BL⊥CP交CP的延长线于点L,交AC于点F,则∠L=90°,
∵CE=CD,∠DCE=30°,P为DE的中点,
∴CP⊥DE,∠DCP=∠ECP∠DCE=15°,
∴PD∥LF,
∵∠ABC=90°,∠A=60°,BC=6,
∴∠ACB=90°﹣∠A=30°,
∴∠LCB=∠ACB+∠DCP=45°,
∴∠LBC=∠LCB=45°,
∴∠ABF=∠ABC﹣∠LBC=45°,
作FH⊥AB于点H,则∠AHF=∠BHF=90°,
∵tan45°=1,tan60°,cos60°,
∴BH=FHAH,AF=2AH,
∵tan60°,
∴ABBC6=2,
∴AH+AH=2,
∴AH=3,
∴AF=2AH=6﹣2,
∵BP≥BL,
∴当点P与点L重合时,BP=BL,此时BP的值最小,
∵点点P与点L重合时,点D与点F重合,
∴AD=AF=6﹣2,
∴当BP取得最小值时,AD的长为6﹣2,
故答案为:6﹣2.
11.【解答】解:如图所示,连接AM,将AM绕点A逆时针旋转60°得到AE,连接PM,ME,QE,
∵,
∴,
∵AM=AE,AP=AQ,∠PAQ=∠MAE=60°,
∴△AME是等边三角形,
∴,
∵∠PAQ﹣∠MAQ=∠MAE﹣∠MAQ,
∴∠PAM=∠QAE,
∴△PAM≌△QAE(SAS),
∴QE=PM=1,
∴点Q在以点E 为圆心、1 为半径的圆上运动,
如图,
∴当点Q在线段ME上时,MQ的值最小,最小值为,当点Q在射线ME上时,MQ有最大值,最大值为,
故答案为:,.
三、解答题
12.【解答】(1)证明:∵线段AD是由AG旋转90°得到的,
∴△DAG是等腰直角三角形,
∴∠DAG=90°,DA=AG.
∵DE⊥AC,
∴∠AED=∠AEF=90°,
∴∠ADE+∠DAE=90°.
∵∠DAE+∠GAC=90°,
∴∠ADE=∠GAC.
∵∠ABC=90°,AB=BC,
∴∠C=∠BAC=45°,
∴∠AFE=∠C=45°,
∴△AFD≌△GCA(AAS).
(2)证明:如图,过点AH⊥AF,交DF于点H,则∠FAH=90°.
∵AE⊥FM,
∴△AEF和△AEH都是等腰直角三角形,
∴AE=EF=EH,
∴FH=EF+EH=2AE.
∵∠DAG=∠FAH=90°,
∴∠DAG﹣∠GAH=∠FAH﹣∠GAH,即∠DAH=∠FAG.
∵DA=AG,
∴△DAH≌△GAF(SAS).
∴DH=FG,
∴DF=DH+FH=FG+2AE.
(3)解:由(1)可知△AFD≌△GCA,
∴AF=CG,
∴△BFG是等腰直角三角形.
∵BF=AF,
∴FGBF=2,AE=EFAF=1.
由(1)可知DF=FG+2AE,
∴DF=2+2×1=4.
∵∠GFE=∠AEF=90°,∠FNG=∠ENA,
∴△FNG∽△ENA,
∴,
∴FN=2EN.
∵EF=FN+EN=1,
∴3EN=1,
∴EN,FN.
∵DE=DF﹣EF=4﹣1=3,
∴DN=EN+DE.
∵EM∥FG,
∴△DEM∽△DFG,
∴,即,
解得EM,
∴DN EM,
∴△DNM的面积为.
13.【解答】解:(1)如图,△A1B1C即为所求;
(2)如图,△A2B2C2即为所求;
(3)将△A1B1C绕某一点旋转可以得到△A2B2C2,旋转中心Q的坐标(1.5,﹣1);
(4)如图,点P即为所求,P点坐标(﹣2,0).
14.【解答】解:(1)思路一:将△ACM绕点C逆时针旋转90°,得到△BCM',连接M'N,
∴△BCM'≌△ACM,
∴BM'=AM,∠BCM'=∠ACM,∠A=∠CBM'=45°,
∴∠ABM'=90°,
∴BN2+BM'2=M'N2,
∵∠MCN=45°,∠ACB=90°,
∴∠M'CB+∠BCN=∠ACM+∠BCN=∠ACB﹣∠MCN=45°,
∵CM'=CM,CN=CN,
∴△NCM≌△NCM'(SAS),
∴MN=M'N,
∴AM2+BN2=MN2,
当AM=2,MN=4时,
∴(2)2+BN2=42,
∴BN=2,
思路二:将△BCN绕点C顺时针旋转90°,得△ACN',连接MN',
∴BN=AN',∠CAN'=∠CBA=45°,∠ACN'=∠BCN,
∴∠N'AB=90°,
∴AN'2+AM2=MN'2,
∵∠MCN=45°,
∴∠ACM+∠BCN=∠ACM+∠ACN'=45°,
∴∠MCN=∠MCN',
∵CN'=CN,CM=CM,
∴△NCM≌△N'CM(SAS),
∴MN=MN',
∴AM2+BN2=MN2,
当AM=2,MN=4时,
∴(2)2+BN2=42,
∴BN=2,
(2)将△ACM绕点C逆时针旋转60°,得到△BCG,连接GN,
∴△BCG≌△ACM,
∴BG=AM,∠BCG=∠ACM,∠A=∠CBG=60°,
∴∠ABG=120°,
同(1)可知△NCM≌△NCG(SAS),
∴MN=GN,
过点G作GH⊥AB于点H,则∠NHG=90°,∠GBH=60°,
设BN=x,
∴MN=AB﹣AM﹣NB=6﹣x,
∵AM=BG=2,
∴BH=1,GH,
∵NH2+GH2=NG2,
∴,
解得x,
∴MN=6.
21世纪教育网(www.21cnjy.com)
同课章节目录
