2025年九年级中考数学三轮冲刺训练三角形相似压轴题训练(含答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练三角形相似压轴题训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练三角形相似压轴题训练
选择题
1.如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD;④△AMN∽△CAB.正确的有( )
A.①②③④ B.①②③ C.①②④ D.②③④
2.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
①△BDE∽△DPE;②;③DP2=PH PB;④tan∠DBE=2.
其中正确的是( )
A.①②③④ B.①②④ C.②③④ D.①③④
3.如图,已知E,F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°,AE、AF分别交对角线BD于点M、N,则下列结论:①∠AEB=∠AEF;②△ABN∽△MDA;③AM AE=AN AF;④BM2+DN2=MN2.其中正确的结论有( )
A.①②④ B.②③④ C.①③ D.①②③④
4.如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D的对称点为点F,EF为交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE∽△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ GD,正确的是( )
A.1个 B.2个 C.3个 D.4个
5.如图,在面积为4的正方形ABCD中,O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G,下列结论:①△FOC≌△EOB;②△OGE∽△FGC;③四边形CEOF的面积为1;④DF2+BE2=2OG OC.其中结论正确的序号有( )
A.①②③ B.①② C.③④ D.①②③④
二、填空题
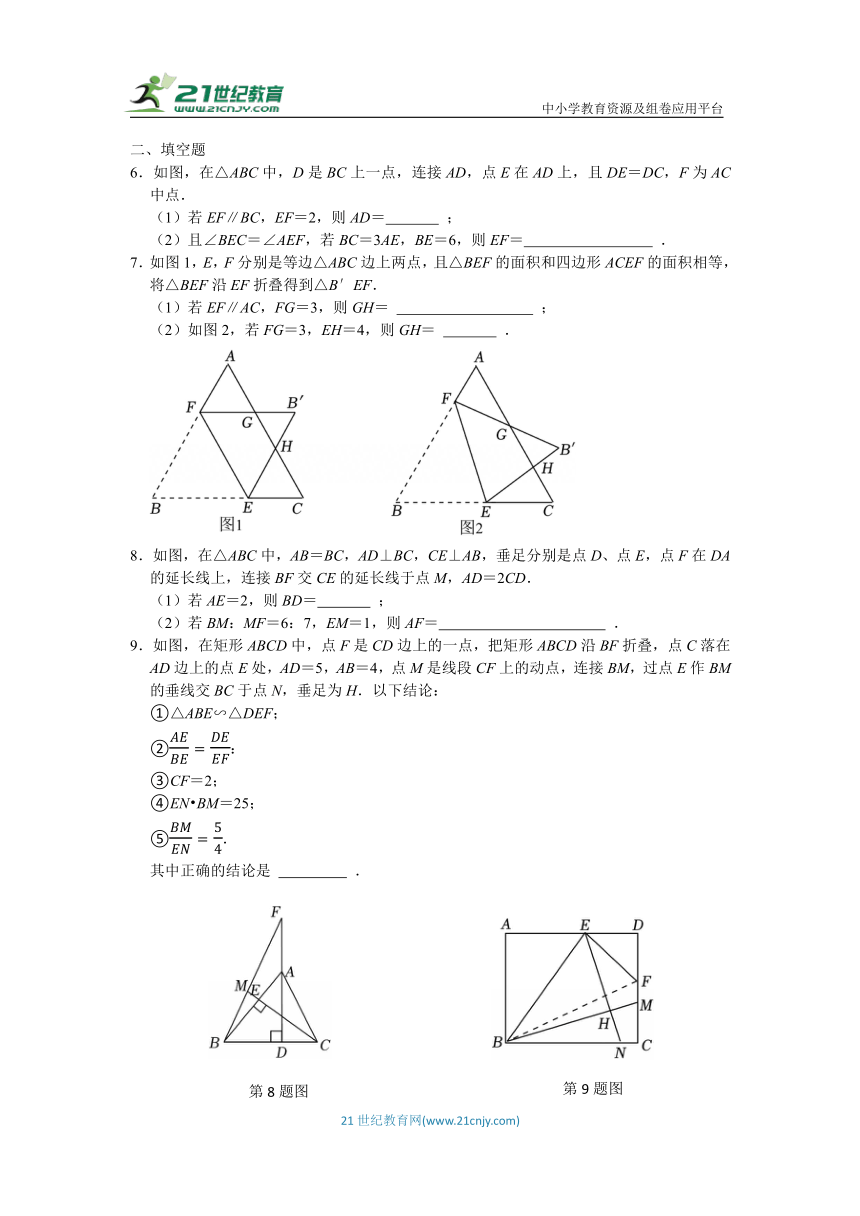
6.如图,在△ABC中,D是BC上一点,连接AD,点E在AD上,且DE=DC,F为AC中点.
(1)若EF∥BC,EF=2,则AD= ;
(2)且∠BEC=∠AEF,若BC=3AE,BE=6,则EF= .
7.如图1,E,F分别是等边△ABC边上两点,且△BEF的面积和四边形ACEF的面积相等,将△BEF沿EF折叠得到△B′EF.
(1)若EF∥AC,FG=3,则GH= ;
(2)如图2,若FG=3,EH=4,则GH= .
8.如图,在△ABC中,AB=BC,AD⊥BC,CE⊥AB,垂足分别是点D、点E,点F在DA的延长线上,连接BF交CE的延长线于点M,AD=2CD.
(1)若AE=2,则BD= ;
(2)若BM:MF=6:7,EM=1,则AF= .
9.如图,在矩形ABCD中,点F是CD边上的一点,把矩形ABCD沿BF折叠,点C落在AD边上的点E处,AD=5,AB=4,点M是线段CF上的动点,连接BM,过点E作BM的垂线交BC于点N,垂足为H.以下结论:
①△ABE∽△DEF;
②:
③CF=2;
④EN BM=25;
⑤.
其中正确的结论是 .
三、解答题
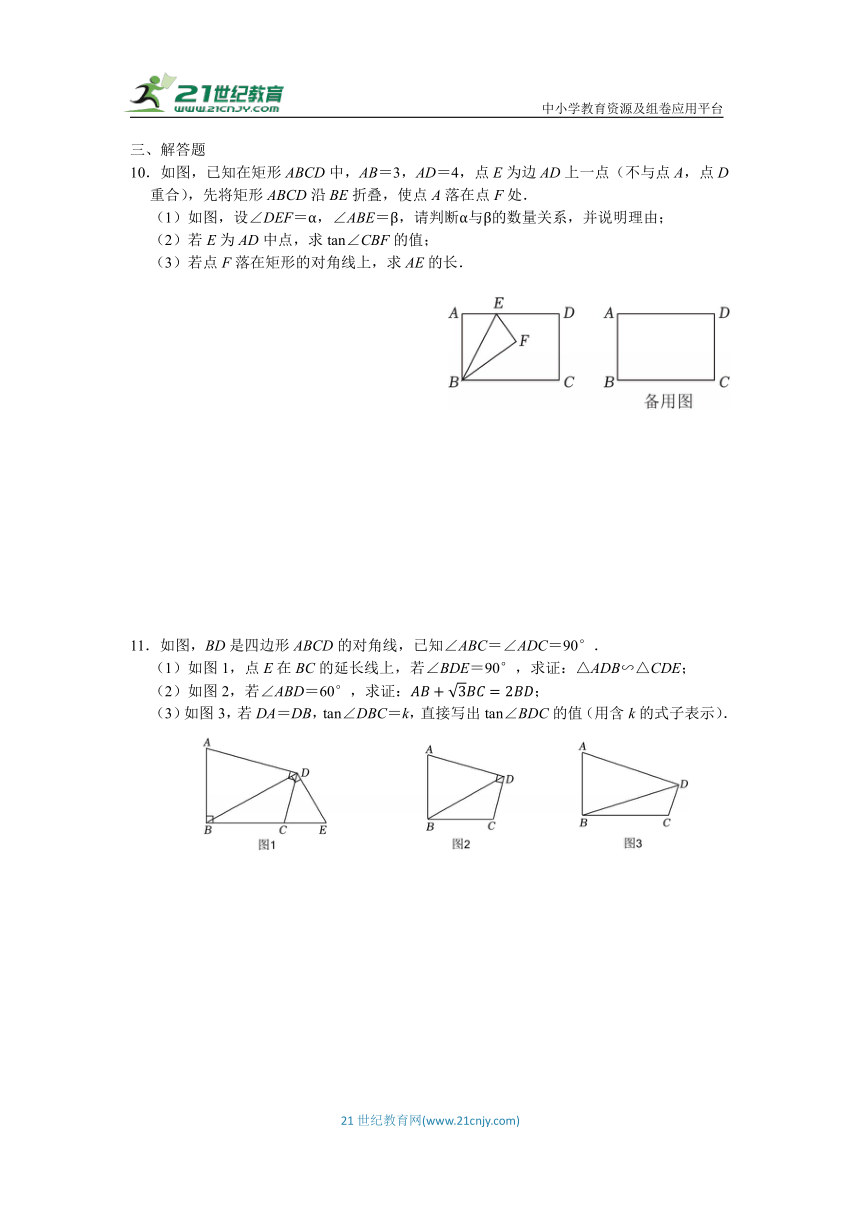
10.如图,已知在矩形ABCD中,AB=3,AD=4,点E为边AD上一点(不与点A,点D重合),先将矩形ABCD沿BE折叠,使点A落在点F处.
(1)如图,设∠DEF=α,∠ABE=β,请判断α与β的数量关系,并说明理由;
(2)若E为AD中点,求tan∠CBF的值;
(3)若点F落在矩形的对角线上,求AE的长.
11.如图,BD是四边形ABCD的对角线,已知∠ABC=∠ADC=90°.
(1)如图1,点E在BC的延长线上,若∠BDE=90°,求证:△ADB∽△CDE;
(2)如图2,若∠ABD=60°,求证:;
(3)如图3,若DA=DB,tan∠DBC=k,直接写出tan∠BDC的值(用含k的式子表示).
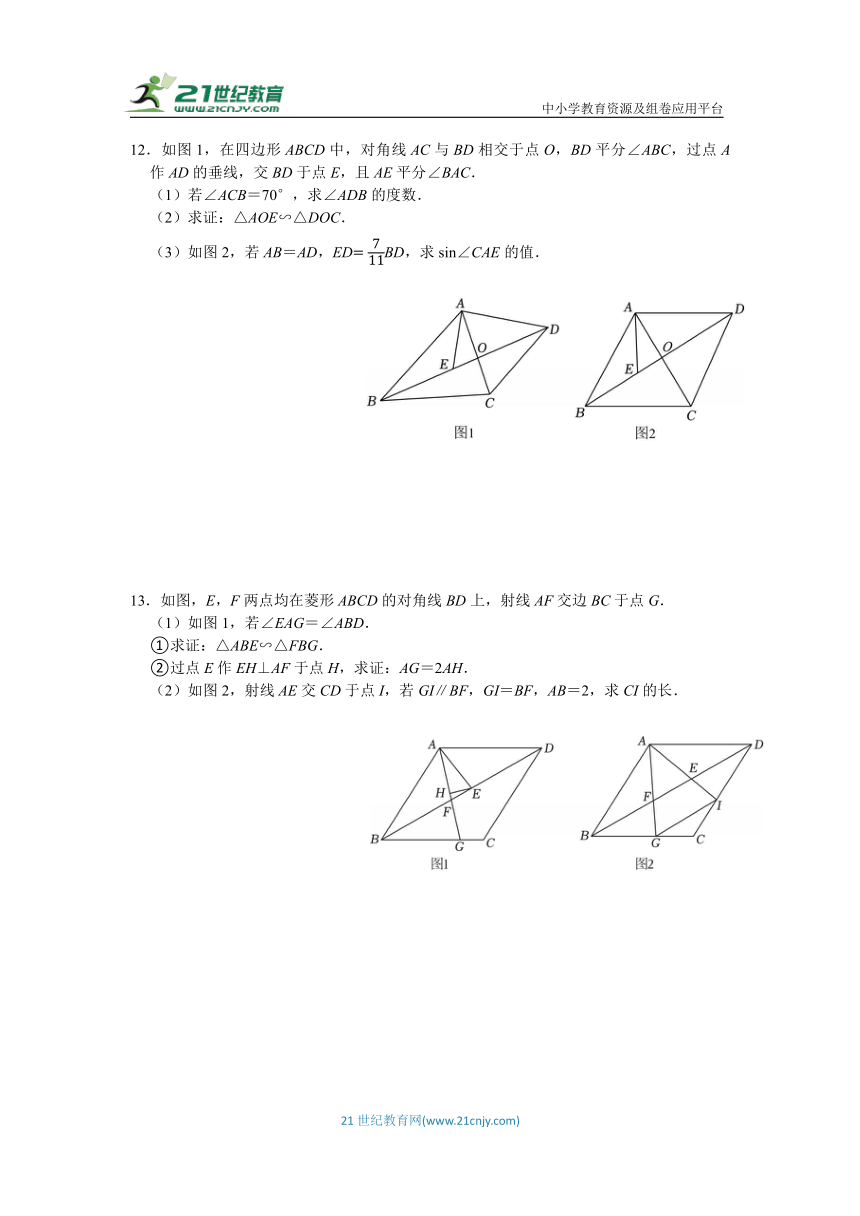
12.如图1,在四边形ABCD中,对角线AC与BD相交于点O,BD平分∠ABC,过点A作AD的垂线,交BD于点E,且AE平分∠BAC.
(1)若∠ACB=70°,求∠ADB的度数.
(2)求证:△AOE∽△DOC.
(3)如图2,若AB=AD,EDBD,求sin∠CAE的值.
13.如图,E,F两点均在菱形ABCD的对角线BD上,射线AF交边BC于点G.
(1)如图1,若∠EAG=∠ABD.
①求证:△ABE∽△FBG.
②过点E作EH⊥AF于点H,求证:AG=2AH.
(2)如图2,射线AE交CD于点I,若GI∥BF,GI=BF,AB=2,求CI的长.
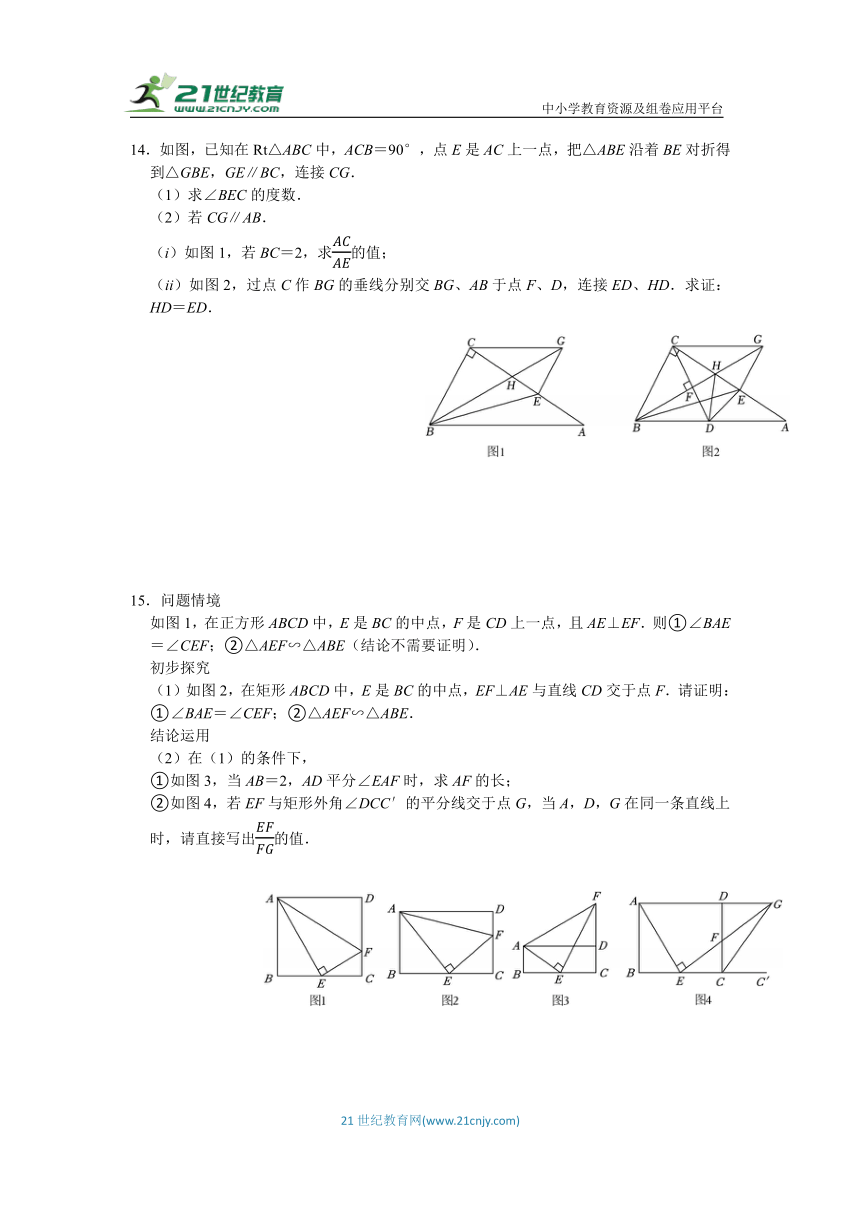
14.如图,已知在Rt△ABC中,ACB=90°,点E是AC上一点,把△ABE沿着BE对折得到△GBE,GE∥BC,连接CG.
(1)求∠BEC的度数.
(2)若CG∥AB.
(i)如图1,若BC=2,求的值;
(ii)如图2,过点C作BG的垂线分别交BG、AB于点F、D,连接ED、HD.求证:HD=ED.
15.问题情境
如图1,在正方形ABCD中,E是BC的中点,F是CD上一点,且AE⊥EF.则①∠BAE=∠CEF;②△AEF∽△ABE(结论不需要证明).
初步探究
(1)如图2,在矩形ABCD中,E是BC的中点,EF⊥AE与直线CD交于点F.请证明:①∠BAE=∠CEF;②△AEF∽△ABE.
结论运用
(2)在(1)的条件下,
①如图3,当AB=2,AD平分∠EAF时,求AF的长;
②如图4,若EF与矩形外角∠DCC′的平分线交于点G,当A,D,G在同一条直线上时,请直接写出的值.
参考答案
一、选择题
1.【解答】解:∵AD∥BC,
∴△AMN∽△CBN,
∴,
∵M是AD边的中点,
∴AM=MDADBC,
∴,
∴CN=2AN,故①正确;
如图,过D作DH∥BM交AC于G,连接NH,
∵DH∥BM,BM⊥AC,
∴DH⊥AC,
∵DH∥BM,AD∥BC,
∴四边形BMDH是平行四边形,
∴BH=MDBC,
∴BH=CH,
∵∠BNC=90°,
∴NH=HC,且DH⊥AC,
∴DH是NC的垂直平分线,
∴DN=CD,故②正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∴∠DAC=∠ACB,∠ABC=∠ANM=90°,
∴△AMN∽△CAB,故④正确;
∵AD∥BC,
∴∠DAC=∠BCA,且∠BAC+∠ACB=90°,∠DAC+∠AMB=90°,
∴∠BAC=∠AMB,且∠BAM=∠ABC,
∴△ABM∽△BCA,
∴,
∴AB2BC2,
∴ABBC,
∵tan∠DAC=tan∠ACB,
∴tan∠DAC,故③错误,
故选:C.
2.【解答】解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴∠CPD=∠CDP=75°,
∴∠PDE=15°,
∵∠PBD=∠PBC﹣∠HBC=60°﹣45°=15°,
∴∠EBD=∠EDP,
∵∠DEP=∠DEB,
∴△BDE∽△DPE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH,
∴,故②错误;
∵∠PDH=∠PCD=30°,
∵∠DPH=∠DPC,
∴△DPH∽△CDP,
∴,
∴PD2=PH CD,
∵PB=CD,
∴PD2=PH PB,故③正确;
如图,过P作PM⊥CD,PN⊥BC,
设正方形ABCD的边长是4,△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°
∴CM=PN=PB sin60°=42,PM=PC sin30°=2,
∵DE∥PM,
∴∠EDP=∠DPM,
∴∠DBE=∠DPM,
∴tan∠DBE=tan∠DPM2,故④正确;
故选:D.
3.【解答】解:如图,把△ADF绕点A顺时针旋转90°得到△ABH,
由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,
∵∠EAF=45°,
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°﹣∠EAF=45°,
∴∠EAH=∠EAF=45°
在△AEF和△AEH中,
,
∴△AEF≌△AEH(SAS),
∴EH=EF,
∴∠AEB=∠AEF,故①正确;
∵∠AMD=∠ABD+∠BAE=45°+∠BAE,∠NAB=∠EAF+∠BAE=45°+∠BAE,
∴∠NAB=∠AMD,
∵∠ABN=∠ADM=45°,
∴△ABN∽△MDA,故②正确;
连接NE,
∵∠MAN=∠MBE=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∵∠MBE=∠EAF=45°,∠AEB=∠AEF,
∴△AFE∽△BME,
∵△AMN∽△BME,
∴△AMN∽△AFE,
∴,
∴AM AE=AN AF,故③正确;
如图,将△ABM绕点A逆时针旋转90°得到△ADG,连接NG,
∴∠ADG=∠ABM=45°,BM=DG,
∴∠GDN=90°,
∴△GDN是直角三角形,
同(1)得△ANG≌△ANM(SAS),
∴MN=GN,
∴MN2=NG2=DN2+DG2=DN2+BM2,故④正确.
本题正确的结论有:①②③④
故选:D.
4.【解答】解:①∵四边形ABCD是正方形,
∴∠A=∠B=∠BCD=∠D=90°.
由折叠可知:∠GEP=∠BCD=90°,∠F=∠D=90°.
∴∠BEP+∠AEG=90°,
∵∠A=90°,
∴∠AEG+∠AGE=90°,
∴∠BEP=∠AGE.
∵∠FGQ=∠AGE,
∴∠BEP=∠FGQ.
∵∠B=∠F=90°,
∴△PBE∽△QFG.
故①正确;
②过点C作CM⊥EG于M,
由折叠可得:∠GEC=∠DCE,
∵AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠GEC,
在△BEC和△MEC中,
,
∴△BEC≌△MEC(AAS).
∴CB=CM,S△BEC=S△MEC.
∵CG=CG,
∴Rt△CMG≌Rt△CDG(HL),
∴S△CMG=S△CDG,
∴S△CEG=S△BEC+S△CDG>S△BEC+S四边形CDQH,
∴②不正确;
③由折叠可得:∠GEC=∠DCE,
∵AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠GEC,
即EC平分∠BEG.
∴③正确;
④连接DH,MH,HE,如图,
∵△BEC≌△MEC,△CMG≌△CDG,
∴∠BCE=∠MCE,∠MCG=∠DCG,
∴∠ECG=∠ECM+∠GCM∠BCD=45°,
∵EC⊥HP,
∴∠CHP=45°.
∴∠GHQ=∠CHP=45°.
由折叠可得:∠EHP=∠CHP=45°,
∴EH⊥CG.
∴EG2﹣EH2=GH2.
由折叠可知:EH=CH.
∴EG2﹣CH2=GH2.
∵CM⊥EG,EH⊥CG,
∴∠EMC=∠EHC=90°,
∴E,M,H,C四点共圆,
∴∠HMC=∠HEC=45°.
在△CMH和△CDH中,
,
∴△CMH≌△CDH(SAS).
∴∠CDH=∠CMH=45°,
∵∠CDA=90°,
∴∠GDH=45°,
∵∠GHQ=∠CHP=45°,
∴∠GHQ=∠GDH=45°.
∵∠HGQ=∠DGH,
∴△GHQ∽△GDH,
∴,
∴GH2=GQ GD,
∴GE2﹣CH2=GQ GD.
∴④正确;
综上可得,正确的结论有:①③④.
故选:C.
5.【解答】解:①如图,∵四边形ABCD是正方形,
∴OC=OB,AC⊥BD,∠OCF=∠OBE=45°,
∵∠MON=90°,
∴∠BOE=∠COF,
∴△BOE≌△COF(ASA),
故①正确;
②∵∠EOF=∠ECF=90°,
∴点O,E,C,F四点共圆,
∴∠EOG=∠CFG,∠OEG=∠FCG,
∴△OGE∽△FGC,
故②正确;
③∵△BOE≌△COF,
∴S△BOE=S△COF,
∴S四边形CEOF=S△BOCS正方形ABCD=1,
故③正确;
④∵△COE≌△DOF,
∴OE=OF,
又∵∠EOF=90°,
∴△EOF是等腰直角三角形,
∴∠OEG=45°=∠OCE,
∵∠EOG=∠COE,
∴△OEG∽△OCE,
∴,
∴OG OC=OE2,
∵OC,OE,
∴OG AC=EF2,
∵CE=DF,BC=CD,
∴BE=CF,
在Rt△CEF中,CF2+CE2=EF2,
∴BE2+DF2=EF2,
∴OG AC=BE2+DF2,
∴DF2+BE2=2OG OC,
故④正确,
故选:D.
二、填空题
6.【解答】解:(1)∵EF∥BC,
∴∠AEF=∠ADC,∠AFE=∠ACD,
∴△AEF∽△ADC,
∴,
∵F为AC中点,
∴,即E为AD的中点,
∴,
∴,AE=DE,
∵EF=2,
∴DC=2EF=2×2=4,
∵DE=DC,
∴DE=DC=4,
∴AD=2DE=2×4=8.
故答案为:8;
(2)如图,过C作AD的平行线,交EF的延长线于G,
∵DE=DC,
∴∠DEC=∠DCE,
∵CG∥AD,
∴∠GCE=∠DEC,∠AEG=∠G,
∴∠DCE=∠GCE,
∵∠BEC=∠AEF,
∴∠BEC=∠G,
∴△BEC∽△EGC,
∴,
∴CE2=CG BC,
∵F为AC中点,
∴AF=CF,
在△AEF和△CGF中,
,
∴△AEF≌△CGF(ASA),
∴AE=CG,EF=GF,
∴,
∵BC=3AE,BE=6,CE2=CG BC,
又∵AE=CG,
∴CE2=AE×3AE=3AE2,
则,
由得,
解得,
∵,
∴.
故答案为:.
7.【解答】解:(1)过点A作AM⊥FG于点M,如图1:
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC,
∵EF∥AC,
∴∠BEF=∠C=60°,∠BFE=∠A=60°,
∴△BEF为等边三角形,
∴BE=BF,
∴AB﹣BF=BC﹣BE,
∴AF=CE,
根据折叠可知:∠BFE=∠EFB′=60°,∠BEF=∠B′EF=60°,
∴∠AFG=180°﹣∠BFE﹣∠EFB′=180°﹣60°﹣60°=60°,∠CEH=180°﹣∠BEF﹣∠B′EF=180°﹣60°﹣60°=60°,
∴△AFG和△CEH为等边三角形,
∴∠B′GH=∠AGF=60°,∠GHB′=∠CHE=60°,AG=AF=FG,CE=CH=EH,
∴AG=AF=FG=CE=CH=EH,
根据折叠可知:△B′EF为等边三角形,
∴B′F=B′E,
∴B′F﹣FG=B′E﹣EH,
∴B′G=B′H,
∴△B′GH为等边三角形,
∵△AFG为等边三角形,AM⊥FG,
∴,
∴,
∴,
同理得:,
∵△BEF的面积和四边形ACEF的面积相等,
∴S△B′EF=S△BEF=S四边形ACEF,
∴S△B′GH+S四边形GHEF=S四边形GHEF+S△AFG+S△CEH,
∵△AFG和△CEH为等边三角形,且FG=CE,
∴S△AFG=S△CEH,
∴S△B′GH=2S△AFG,
∴,
解得:,(负值已舍去),
故答案为:;
(2)∵△BEF的面积和四边形ACEF的面积相等,
∴S△B′EF=S△BEF=S四边形ACEF,
∴S△B′GH+S四边形GHEF=S四边形GHEF+S△AFG+S△CEH,
∴S△AFG+S△HEC=S△B′GH,
∵∠B′=∠A=60°,∠AGF=∠B′GH,
∴△AFG∽△B′HG,
同理得:△B′HG∽△CHE,
∴,,
∴,
∴,
∴HG2=FG2+EH2=32+42,
解得:HG=5,(负值已舍去),
故答案为:5.
8.【解答】(1)解:∵BA=BC,
∴∠BAC=∠BCA,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(AAS);
∴BD=BE,∠BAD=∠BCE,
∴∠DAC=∠ACE,
∵∠AEC=∠ADC=90°,AC=CA,
∴△ADC≌△CEA(AAS),
∴AE=CD=2,
∴AD=2CD=4,
设BE=BD=x,
在Rt△ABD中,则有(x+2)2=x2+42,
∴x=3,
∴BD=3;
故答案为:3;
(2)解:过F作FH⊥BA交BA的延长线于H,
由(1)知:△ADC≌△CEA(AAS),
∴AE=CD,
∵AD⊥BC,AD=2CD,
设AD=2a,则DC=a,
设BE=BD=x,
在Rt△ABD中,则有(x+a)2=x2+(2a)2,
∴xa,
∴BDa,
∵△ABD≌△CBE(AAS),
∴BD=BEa,
∵CE⊥AB,FH⊥BA,
∴EM∥FH,
∴△BEM∽△BHF,
∴,
∵BM:MF=6:7,
∴BM:BF=6:13,
∵EM=1,
∴,
∴FH,
∵∠BAD=∠FAH,∠ADB=∠FHA=90°,
∴△AFH∽△ABD,
∴,
∵AB=AE+BE=aaa,BDa,
∴,
∴AF.
故答案为:.
9.【解答】解:∵矩形ABCD沿BF折叠,点C落在AD边上的点E处,
∴∠BEF=∠C=90°=∠A,BC=BE,EF=CF,
∴∠FED=90°﹣∠AEB=∠ABE,
∴△ABE∽△DEF,故①正确;
∴,
∴,故②错误;
由翻折可知:BE=BC=5,
∵AB=4,
∴AE3,
∴DE=AD﹣AE=5﹣3=2,
设EF=x=CF,则DF=4﹣x,
在Rt△DEF中,DE2+DF2=EF2,
∴22+(4﹣x)2=x2,
解得:x=2.5,
∴CF=2.5,故③错误;
过E作EG⊥BC于G,连接EC,如图:
在Rt△BFC中,BF,
在Rt△EGC中,EC2,
∴BF EC225,
∵BF≠BM,EC≠EN,
∴EN BM≠25,故④错误;
∵BM⊥EN,
∴∠BHN=90°,
∴∠BNH=90°﹣∠NBH=∠BMC,即∠ENG=∠BMC,
∵∠EGN=90°=∠C,
∴△EGN∽△BCM,
∴,故⑤正确;
∴正确的结论是①⑤,
故答案为:①⑤.
三、解答题
10.【解答】解:(1)∠ABE=β=∠FBE,
则∠AEB=90°﹣β=∠BEF,
则∠AEB+∠FEB+∠FED=180°,即90°﹣β+90°﹣β+α=180°,
则α=2β;
(2)如图,∵E为AD中点,则AE=EF=2,
过点F作MN⊥AB交AD于点M,交BC于点N,
设MF=x,则FN=4﹣x,则ME,
∵∠MEF+∠MFE=90°,∠BFN+∠FBN=90°,
∴∠FBC=∠EFM,
∴sin∠FBC=sin∠EFM,即FN:BF=EM:EF,
即(3﹣x):3:2,解得:x,
则sin∠FBC=FN:BF=(3﹣x):3;
(3)当点F在BD上时,如图,
∵AB=3=AF,AD=4,则BD=5,则FD=BD﹣BF=5﹣3=2,
设AE=EF=x,则ED=4﹣x,
在Rt△EFD中,ED2=EF2+FD2,即(4﹣x)2=x2+4,
则x=1.5=AE;
当点F在AC上时,
同理可得:∠DAC=∠ABE,
则tan∠DAC=tan∠ABE,即AE:AB=CD:AD,即AE:3=3:4,
则AE,
综上,AE或.
11.【解答】(1)证明:∵∠ABC=∠ADC=90°,
∴∠A+∠BCD=360°﹣90°﹣90°=180°,
∵∠BCD+∠DCE=180°,
∴∠A=∠DCE,
∵DE⊥BD,
∴∠BDC+∠CDE=90°,
∵∠ADB+∠BDC=90°,
∴∠ADB=∠CDE,
∴△ADB∽△CDE.
(2)证明:过D点作DE⊥BD,交BC 的延长线于E点,
由(1)可得,△ADB∽△CDE,
∴,∠E=∠ABD=60°,
∵DE⊥BD,
∴∠BDE=90°,
∴∠DBE=30°,
∴BE=2DE,
∴,
∴,,
∴,BEBD,
,
即,
在等式两边都乘以,
∴;
(3)解:过D点作DE⊥BD,交BC 的延长线于E点,
由(1)可得,△ADB∽△CDE,
∴,
设DA=DB=1,则DC=DE,
∵∵DE⊥BD,
∴∠BDE=90°,
∴tan∠DBCk,
∴DE=DC=k,
过C作CF⊥DB于点F,设BF=x(0<x<1),
则DF=BD﹣BF=1﹣x,
在Rt△BFC中,tank,
∴CF=kx,
在Rt△DCF中,DF2+CF2=CD2,
∴(1﹣x)2+(kx)2=k2,
整理得(k2+1)x﹣2x+1﹣k2=0,
即[(k2+1)x﹣(1﹣k2)](x﹣1)=0,
解得x1,x2=1(舍去),
∴DF=1﹣x,
∴tan∠BDC.
12.【解答】(1)解:∵BD平分∠ABC,
∴∠ABEABC,
∵AE平分∠BAC,
∴∠BAEBAC,
∵∠AED=∠ABE+∠EBA,
∴∠AED(∠ABC+∠BAC).
∵∠ACB=70°,
∴∠ABC+∠BAC=180°﹣∠ACB=110°,
∴∠AED=55°,
∵AE⊥AD,
∴∠ADB=90°﹣∠AED=35°;
(2)证明:过点E作EF⊥BC于点F,EG⊥AB于点G,EH⊥AC于点H,连接CE,如图,
∵BD平分∠ABC,EF⊥BC,EG⊥AB,
∴EF=EG,
∵AE平分∠BAC,EH⊥AC,EG⊥AB,
∴EH=EG,
∴EF=EH,
∵EF⊥BC,EH⊥AC,
∴点E在∠ACB的平分线上,
∴∠ACEACB.
由(1)知:∠AED(∠ABC+∠BAC)=90°∠ACB,
∴∠AED=90°﹣∠ACE,
∵AE⊥AD,
∴∠ADB=90°﹣∠AED,
∴∠ACE=∠ADB,
∵∠EOC=∠AOD,
∴△EOC∽△AOD,
∴,
∵∠AOE=∠DOC,
∴△AOE∽△DOC;
(3)解:延长AE,交BC于点F,如图,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ADB=∠CBD,
∴AD∥BC,
∴△AED∽△FEB,
∴,
∵EDBD,
∴.
设AD=7k,则DF=4k,AB=AD=7k,
∵AE⊥AD,AD∥BC,
∴AF⊥BC,
∴sin∠BAF.
∵AE平分∠BAC,
∴∠CAE=∠BAF,
∴sin∠CAE=sin∠BAF.
13.【解答】(1)①证明:∵四边形ABCD为菱形,
∴∠ABD=∠GBF.
∵∠EAG=∠ABD,
∴∠EAG=∠GBF.
∵∠BFG=∠AFE,
∴△BFG∽△AFE,
∴∠AEB=∠BGF.
∵∠ABE=∠GBF,
∴△ABE∽△FBG;
②证明:连接EG,如图,
由(1)①得:△AFE∽△BFG,
∴.
∵∠EFG=∠AFB,
∴△AFB∽△EFG,
∴∠EGF=∠ABD.
∵∠EAG=∠ABD,
∴∠EAG=∠EGF,
∴EA=EG.
∵EH⊥AF,
∴AH=HG,
∴AG=2AH.
(2)解:连接FI,如图,
∵GI∥BF,GI=BF,
∴四边形BGIF为平行四边形.
∴FI∥BC,
∴.
∵四边形ABCD为菱形,
∴AD∥BC,
∴△ADF∽△GBF,
∴,
∴.
∵四边形ABCD为菱形,
∴AB=CD=BC=AD=2,
∴∠CBD=∠CDB,
∵GI∥BF,
∴∠CBD=∠CGI,∠CIG=∠CDB,
∴∠CGI=∠CIG,
∴CI=CG.
设CI=CG=x,则DI=BG=2﹣x,
∴,
解得:(不合题意,舍去),
即CI的长为.
14.【解答】(1)解:如图1中,连接AG,延长BE交AG于点J.
∵GE∥BC,
∴∠BCA=∠CEG=90°,
∴∠CAEG=90°,
由翻折变换的性质可知BE垂直平分线段AG,EG=EA,
∴∠GEJ=∠AEJ=45°,
∴∠BEC=45°;
(2)①解:设AE=EG=x,
∵BC∥EG,
∴∠CBH=∠EGH,
由翻折变换的性质可知∠BAE=∠BGE,
∴∠CBH=∠BAC,
∵∠BCH=∠BCA=90°,
∴△BCH∽∠ACB,
∴BC2=CH CA,
∴CH
∵CG∥AB,
∴∠GCH=∠CAB,
∴∠EGH=∠GCE,
∵∠GEH=∠GEC,
∴△GEH∽△CEG,
∴GE2=EH EC,
∴x2=(2)×2,
解得x1(负根已经舍去),
经检验x1是分式方程的解,
∴AE1,AC1,
∴;
②证明:
∵BC∥EG,
∴∠BCH=∠CEG,
∵∠CBH=∠A=∠BGE=∠ECG,CB=CE,
∴△CBH≌△ECG(ASA),
∴CH=GE=AE,
∵∠DCA+∠BCF=90°,∠CBH+∠BCF=90°,
∴∠DCA=∠CBH=∠A,
∴DC=DA,
∴△DHC≌△DEA(SAS),
∴DH=DE.
15.【解答】(1)证明:①∵四边形ABCD是矩形,EF⊥AE与直线CD交于点F,
∴∠B=∠C=90°,∠AEF=90°,
∴∠BAE+∠AEB=∠AEB+∠CEF,
∴∠BAE=∠CEF;
②∵EF⊥AE与直线CD交于点F,
∴∠AEF=∠B=∠C=90°,
∵由①得∠BAE=∠CEF,
∴△ABE∽△ECF,
∴,
在矩形ABCD中,E是BC的中点,
设AB=x、BE=CE=y、AE=a,
∵,
∴,
∴,
∴,,
∴且∠AEF=∠B=90°,
∴△AEF∽△ABE;
(2)解:①∵AD平分∠EAF,
∴∠FAD=∠DAE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AEB,
∴∠FAD=∠AEB,
∵∠FDA=∠B=90°,
∴△ABE∽△FDA,
设BE=EC=x,则AD=2x,
∴,
∴∠AFE=30°,
由(1)得△AEF∽△ABE,
∴∠AFE=∠AEB,
∴∠AFE=∠AEB=30°,
∴AE=2AB=4,
∴,
∴AF=8.
②;理由如下:
∵∠ECF=∠GDF=90°,∠CFE=∠DFG,
∴△ECF∽△GDF,
设AB=CD=x,BE=EC=y,
∵CG平分∠DCC′,
∴∠DCG=∠GCC′=45°,
∵AG∥BC′,
∴∠DGC=∠GCC′=45°,
∴DG=DC=x,
∴.
∵由(1)得△ABE∽△ECF,
∴,
∴,
∴,,
∵,
∴,
∴,
∴xy=x2﹣y2,
∴,
设,
∴t=1﹣t2,
解得:,(t2<0,舍去),
∴.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练三角形相似压轴题训练
选择题
1.如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD;④△AMN∽△CAB.正确的有( )
A.①②③④ B.①②③ C.①②④ D.②③④
2.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
①△BDE∽△DPE;②;③DP2=PH PB;④tan∠DBE=2.
其中正确的是( )
A.①②③④ B.①②④ C.②③④ D.①③④
3.如图,已知E,F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°,AE、AF分别交对角线BD于点M、N,则下列结论:①∠AEB=∠AEF;②△ABN∽△MDA;③AM AE=AN AF;④BM2+DN2=MN2.其中正确的结论有( )
A.①②④ B.②③④ C.①③ D.①②③④
4.如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D的对称点为点F,EF为交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE∽△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ GD,正确的是( )
A.1个 B.2个 C.3个 D.4个
5.如图,在面积为4的正方形ABCD中,O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G,下列结论:①△FOC≌△EOB;②△OGE∽△FGC;③四边形CEOF的面积为1;④DF2+BE2=2OG OC.其中结论正确的序号有( )
A.①②③ B.①② C.③④ D.①②③④
二、填空题
6.如图,在△ABC中,D是BC上一点,连接AD,点E在AD上,且DE=DC,F为AC中点.
(1)若EF∥BC,EF=2,则AD= ;
(2)且∠BEC=∠AEF,若BC=3AE,BE=6,则EF= .
7.如图1,E,F分别是等边△ABC边上两点,且△BEF的面积和四边形ACEF的面积相等,将△BEF沿EF折叠得到△B′EF.
(1)若EF∥AC,FG=3,则GH= ;
(2)如图2,若FG=3,EH=4,则GH= .
8.如图,在△ABC中,AB=BC,AD⊥BC,CE⊥AB,垂足分别是点D、点E,点F在DA的延长线上,连接BF交CE的延长线于点M,AD=2CD.
(1)若AE=2,则BD= ;
(2)若BM:MF=6:7,EM=1,则AF= .
9.如图,在矩形ABCD中,点F是CD边上的一点,把矩形ABCD沿BF折叠,点C落在AD边上的点E处,AD=5,AB=4,点M是线段CF上的动点,连接BM,过点E作BM的垂线交BC于点N,垂足为H.以下结论:
①△ABE∽△DEF;
②:
③CF=2;
④EN BM=25;
⑤.
其中正确的结论是 .
三、解答题
10.如图,已知在矩形ABCD中,AB=3,AD=4,点E为边AD上一点(不与点A,点D重合),先将矩形ABCD沿BE折叠,使点A落在点F处.
(1)如图,设∠DEF=α,∠ABE=β,请判断α与β的数量关系,并说明理由;
(2)若E为AD中点,求tan∠CBF的值;
(3)若点F落在矩形的对角线上,求AE的长.
11.如图,BD是四边形ABCD的对角线,已知∠ABC=∠ADC=90°.
(1)如图1,点E在BC的延长线上,若∠BDE=90°,求证:△ADB∽△CDE;
(2)如图2,若∠ABD=60°,求证:;
(3)如图3,若DA=DB,tan∠DBC=k,直接写出tan∠BDC的值(用含k的式子表示).
12.如图1,在四边形ABCD中,对角线AC与BD相交于点O,BD平分∠ABC,过点A作AD的垂线,交BD于点E,且AE平分∠BAC.
(1)若∠ACB=70°,求∠ADB的度数.
(2)求证:△AOE∽△DOC.
(3)如图2,若AB=AD,EDBD,求sin∠CAE的值.
13.如图,E,F两点均在菱形ABCD的对角线BD上,射线AF交边BC于点G.
(1)如图1,若∠EAG=∠ABD.
①求证:△ABE∽△FBG.
②过点E作EH⊥AF于点H,求证:AG=2AH.
(2)如图2,射线AE交CD于点I,若GI∥BF,GI=BF,AB=2,求CI的长.
14.如图,已知在Rt△ABC中,ACB=90°,点E是AC上一点,把△ABE沿着BE对折得到△GBE,GE∥BC,连接CG.
(1)求∠BEC的度数.
(2)若CG∥AB.
(i)如图1,若BC=2,求的值;
(ii)如图2,过点C作BG的垂线分别交BG、AB于点F、D,连接ED、HD.求证:HD=ED.
15.问题情境
如图1,在正方形ABCD中,E是BC的中点,F是CD上一点,且AE⊥EF.则①∠BAE=∠CEF;②△AEF∽△ABE(结论不需要证明).
初步探究
(1)如图2,在矩形ABCD中,E是BC的中点,EF⊥AE与直线CD交于点F.请证明:①∠BAE=∠CEF;②△AEF∽△ABE.
结论运用
(2)在(1)的条件下,
①如图3,当AB=2,AD平分∠EAF时,求AF的长;
②如图4,若EF与矩形外角∠DCC′的平分线交于点G,当A,D,G在同一条直线上时,请直接写出的值.
参考答案
一、选择题
1.【解答】解:∵AD∥BC,
∴△AMN∽△CBN,
∴,
∵M是AD边的中点,
∴AM=MDADBC,
∴,
∴CN=2AN,故①正确;
如图,过D作DH∥BM交AC于G,连接NH,
∵DH∥BM,BM⊥AC,
∴DH⊥AC,
∵DH∥BM,AD∥BC,
∴四边形BMDH是平行四边形,
∴BH=MDBC,
∴BH=CH,
∵∠BNC=90°,
∴NH=HC,且DH⊥AC,
∴DH是NC的垂直平分线,
∴DN=CD,故②正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∴∠DAC=∠ACB,∠ABC=∠ANM=90°,
∴△AMN∽△CAB,故④正确;
∵AD∥BC,
∴∠DAC=∠BCA,且∠BAC+∠ACB=90°,∠DAC+∠AMB=90°,
∴∠BAC=∠AMB,且∠BAM=∠ABC,
∴△ABM∽△BCA,
∴,
∴AB2BC2,
∴ABBC,
∵tan∠DAC=tan∠ACB,
∴tan∠DAC,故③错误,
故选:C.
2.【解答】解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴∠CPD=∠CDP=75°,
∴∠PDE=15°,
∵∠PBD=∠PBC﹣∠HBC=60°﹣45°=15°,
∴∠EBD=∠EDP,
∵∠DEP=∠DEB,
∴△BDE∽△DPE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH,
∴,故②错误;
∵∠PDH=∠PCD=30°,
∵∠DPH=∠DPC,
∴△DPH∽△CDP,
∴,
∴PD2=PH CD,
∵PB=CD,
∴PD2=PH PB,故③正确;
如图,过P作PM⊥CD,PN⊥BC,
设正方形ABCD的边长是4,△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°
∴CM=PN=PB sin60°=42,PM=PC sin30°=2,
∵DE∥PM,
∴∠EDP=∠DPM,
∴∠DBE=∠DPM,
∴tan∠DBE=tan∠DPM2,故④正确;
故选:D.
3.【解答】解:如图,把△ADF绕点A顺时针旋转90°得到△ABH,
由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,
∵∠EAF=45°,
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°﹣∠EAF=45°,
∴∠EAH=∠EAF=45°
在△AEF和△AEH中,
,
∴△AEF≌△AEH(SAS),
∴EH=EF,
∴∠AEB=∠AEF,故①正确;
∵∠AMD=∠ABD+∠BAE=45°+∠BAE,∠NAB=∠EAF+∠BAE=45°+∠BAE,
∴∠NAB=∠AMD,
∵∠ABN=∠ADM=45°,
∴△ABN∽△MDA,故②正确;
连接NE,
∵∠MAN=∠MBE=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∵∠MBE=∠EAF=45°,∠AEB=∠AEF,
∴△AFE∽△BME,
∵△AMN∽△BME,
∴△AMN∽△AFE,
∴,
∴AM AE=AN AF,故③正确;
如图,将△ABM绕点A逆时针旋转90°得到△ADG,连接NG,
∴∠ADG=∠ABM=45°,BM=DG,
∴∠GDN=90°,
∴△GDN是直角三角形,
同(1)得△ANG≌△ANM(SAS),
∴MN=GN,
∴MN2=NG2=DN2+DG2=DN2+BM2,故④正确.
本题正确的结论有:①②③④
故选:D.
4.【解答】解:①∵四边形ABCD是正方形,
∴∠A=∠B=∠BCD=∠D=90°.
由折叠可知:∠GEP=∠BCD=90°,∠F=∠D=90°.
∴∠BEP+∠AEG=90°,
∵∠A=90°,
∴∠AEG+∠AGE=90°,
∴∠BEP=∠AGE.
∵∠FGQ=∠AGE,
∴∠BEP=∠FGQ.
∵∠B=∠F=90°,
∴△PBE∽△QFG.
故①正确;
②过点C作CM⊥EG于M,
由折叠可得:∠GEC=∠DCE,
∵AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠GEC,
在△BEC和△MEC中,
,
∴△BEC≌△MEC(AAS).
∴CB=CM,S△BEC=S△MEC.
∵CG=CG,
∴Rt△CMG≌Rt△CDG(HL),
∴S△CMG=S△CDG,
∴S△CEG=S△BEC+S△CDG>S△BEC+S四边形CDQH,
∴②不正确;
③由折叠可得:∠GEC=∠DCE,
∵AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠GEC,
即EC平分∠BEG.
∴③正确;
④连接DH,MH,HE,如图,
∵△BEC≌△MEC,△CMG≌△CDG,
∴∠BCE=∠MCE,∠MCG=∠DCG,
∴∠ECG=∠ECM+∠GCM∠BCD=45°,
∵EC⊥HP,
∴∠CHP=45°.
∴∠GHQ=∠CHP=45°.
由折叠可得:∠EHP=∠CHP=45°,
∴EH⊥CG.
∴EG2﹣EH2=GH2.
由折叠可知:EH=CH.
∴EG2﹣CH2=GH2.
∵CM⊥EG,EH⊥CG,
∴∠EMC=∠EHC=90°,
∴E,M,H,C四点共圆,
∴∠HMC=∠HEC=45°.
在△CMH和△CDH中,
,
∴△CMH≌△CDH(SAS).
∴∠CDH=∠CMH=45°,
∵∠CDA=90°,
∴∠GDH=45°,
∵∠GHQ=∠CHP=45°,
∴∠GHQ=∠GDH=45°.
∵∠HGQ=∠DGH,
∴△GHQ∽△GDH,
∴,
∴GH2=GQ GD,
∴GE2﹣CH2=GQ GD.
∴④正确;
综上可得,正确的结论有:①③④.
故选:C.
5.【解答】解:①如图,∵四边形ABCD是正方形,
∴OC=OB,AC⊥BD,∠OCF=∠OBE=45°,
∵∠MON=90°,
∴∠BOE=∠COF,
∴△BOE≌△COF(ASA),
故①正确;
②∵∠EOF=∠ECF=90°,
∴点O,E,C,F四点共圆,
∴∠EOG=∠CFG,∠OEG=∠FCG,
∴△OGE∽△FGC,
故②正确;
③∵△BOE≌△COF,
∴S△BOE=S△COF,
∴S四边形CEOF=S△BOCS正方形ABCD=1,
故③正确;
④∵△COE≌△DOF,
∴OE=OF,
又∵∠EOF=90°,
∴△EOF是等腰直角三角形,
∴∠OEG=45°=∠OCE,
∵∠EOG=∠COE,
∴△OEG∽△OCE,
∴,
∴OG OC=OE2,
∵OC,OE,
∴OG AC=EF2,
∵CE=DF,BC=CD,
∴BE=CF,
在Rt△CEF中,CF2+CE2=EF2,
∴BE2+DF2=EF2,
∴OG AC=BE2+DF2,
∴DF2+BE2=2OG OC,
故④正确,
故选:D.
二、填空题
6.【解答】解:(1)∵EF∥BC,
∴∠AEF=∠ADC,∠AFE=∠ACD,
∴△AEF∽△ADC,
∴,
∵F为AC中点,
∴,即E为AD的中点,
∴,
∴,AE=DE,
∵EF=2,
∴DC=2EF=2×2=4,
∵DE=DC,
∴DE=DC=4,
∴AD=2DE=2×4=8.
故答案为:8;
(2)如图,过C作AD的平行线,交EF的延长线于G,
∵DE=DC,
∴∠DEC=∠DCE,
∵CG∥AD,
∴∠GCE=∠DEC,∠AEG=∠G,
∴∠DCE=∠GCE,
∵∠BEC=∠AEF,
∴∠BEC=∠G,
∴△BEC∽△EGC,
∴,
∴CE2=CG BC,
∵F为AC中点,
∴AF=CF,
在△AEF和△CGF中,
,
∴△AEF≌△CGF(ASA),
∴AE=CG,EF=GF,
∴,
∵BC=3AE,BE=6,CE2=CG BC,
又∵AE=CG,
∴CE2=AE×3AE=3AE2,
则,
由得,
解得,
∵,
∴.
故答案为:.
7.【解答】解:(1)过点A作AM⊥FG于点M,如图1:
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC,
∵EF∥AC,
∴∠BEF=∠C=60°,∠BFE=∠A=60°,
∴△BEF为等边三角形,
∴BE=BF,
∴AB﹣BF=BC﹣BE,
∴AF=CE,
根据折叠可知:∠BFE=∠EFB′=60°,∠BEF=∠B′EF=60°,
∴∠AFG=180°﹣∠BFE﹣∠EFB′=180°﹣60°﹣60°=60°,∠CEH=180°﹣∠BEF﹣∠B′EF=180°﹣60°﹣60°=60°,
∴△AFG和△CEH为等边三角形,
∴∠B′GH=∠AGF=60°,∠GHB′=∠CHE=60°,AG=AF=FG,CE=CH=EH,
∴AG=AF=FG=CE=CH=EH,
根据折叠可知:△B′EF为等边三角形,
∴B′F=B′E,
∴B′F﹣FG=B′E﹣EH,
∴B′G=B′H,
∴△B′GH为等边三角形,
∵△AFG为等边三角形,AM⊥FG,
∴,
∴,
∴,
同理得:,
∵△BEF的面积和四边形ACEF的面积相等,
∴S△B′EF=S△BEF=S四边形ACEF,
∴S△B′GH+S四边形GHEF=S四边形GHEF+S△AFG+S△CEH,
∵△AFG和△CEH为等边三角形,且FG=CE,
∴S△AFG=S△CEH,
∴S△B′GH=2S△AFG,
∴,
解得:,(负值已舍去),
故答案为:;
(2)∵△BEF的面积和四边形ACEF的面积相等,
∴S△B′EF=S△BEF=S四边形ACEF,
∴S△B′GH+S四边形GHEF=S四边形GHEF+S△AFG+S△CEH,
∴S△AFG+S△HEC=S△B′GH,
∵∠B′=∠A=60°,∠AGF=∠B′GH,
∴△AFG∽△B′HG,
同理得:△B′HG∽△CHE,
∴,,
∴,
∴,
∴HG2=FG2+EH2=32+42,
解得:HG=5,(负值已舍去),
故答案为:5.
8.【解答】(1)解:∵BA=BC,
∴∠BAC=∠BCA,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(AAS);
∴BD=BE,∠BAD=∠BCE,
∴∠DAC=∠ACE,
∵∠AEC=∠ADC=90°,AC=CA,
∴△ADC≌△CEA(AAS),
∴AE=CD=2,
∴AD=2CD=4,
设BE=BD=x,
在Rt△ABD中,则有(x+2)2=x2+42,
∴x=3,
∴BD=3;
故答案为:3;
(2)解:过F作FH⊥BA交BA的延长线于H,
由(1)知:△ADC≌△CEA(AAS),
∴AE=CD,
∵AD⊥BC,AD=2CD,
设AD=2a,则DC=a,
设BE=BD=x,
在Rt△ABD中,则有(x+a)2=x2+(2a)2,
∴xa,
∴BDa,
∵△ABD≌△CBE(AAS),
∴BD=BEa,
∵CE⊥AB,FH⊥BA,
∴EM∥FH,
∴△BEM∽△BHF,
∴,
∵BM:MF=6:7,
∴BM:BF=6:13,
∵EM=1,
∴,
∴FH,
∵∠BAD=∠FAH,∠ADB=∠FHA=90°,
∴△AFH∽△ABD,
∴,
∵AB=AE+BE=aaa,BDa,
∴,
∴AF.
故答案为:.
9.【解答】解:∵矩形ABCD沿BF折叠,点C落在AD边上的点E处,
∴∠BEF=∠C=90°=∠A,BC=BE,EF=CF,
∴∠FED=90°﹣∠AEB=∠ABE,
∴△ABE∽△DEF,故①正确;
∴,
∴,故②错误;
由翻折可知:BE=BC=5,
∵AB=4,
∴AE3,
∴DE=AD﹣AE=5﹣3=2,
设EF=x=CF,则DF=4﹣x,
在Rt△DEF中,DE2+DF2=EF2,
∴22+(4﹣x)2=x2,
解得:x=2.5,
∴CF=2.5,故③错误;
过E作EG⊥BC于G,连接EC,如图:
在Rt△BFC中,BF,
在Rt△EGC中,EC2,
∴BF EC225,
∵BF≠BM,EC≠EN,
∴EN BM≠25,故④错误;
∵BM⊥EN,
∴∠BHN=90°,
∴∠BNH=90°﹣∠NBH=∠BMC,即∠ENG=∠BMC,
∵∠EGN=90°=∠C,
∴△EGN∽△BCM,
∴,故⑤正确;
∴正确的结论是①⑤,
故答案为:①⑤.
三、解答题
10.【解答】解:(1)∠ABE=β=∠FBE,
则∠AEB=90°﹣β=∠BEF,
则∠AEB+∠FEB+∠FED=180°,即90°﹣β+90°﹣β+α=180°,
则α=2β;
(2)如图,∵E为AD中点,则AE=EF=2,
过点F作MN⊥AB交AD于点M,交BC于点N,
设MF=x,则FN=4﹣x,则ME,
∵∠MEF+∠MFE=90°,∠BFN+∠FBN=90°,
∴∠FBC=∠EFM,
∴sin∠FBC=sin∠EFM,即FN:BF=EM:EF,
即(3﹣x):3:2,解得:x,
则sin∠FBC=FN:BF=(3﹣x):3;
(3)当点F在BD上时,如图,
∵AB=3=AF,AD=4,则BD=5,则FD=BD﹣BF=5﹣3=2,
设AE=EF=x,则ED=4﹣x,
在Rt△EFD中,ED2=EF2+FD2,即(4﹣x)2=x2+4,
则x=1.5=AE;
当点F在AC上时,
同理可得:∠DAC=∠ABE,
则tan∠DAC=tan∠ABE,即AE:AB=CD:AD,即AE:3=3:4,
则AE,
综上,AE或.
11.【解答】(1)证明:∵∠ABC=∠ADC=90°,
∴∠A+∠BCD=360°﹣90°﹣90°=180°,
∵∠BCD+∠DCE=180°,
∴∠A=∠DCE,
∵DE⊥BD,
∴∠BDC+∠CDE=90°,
∵∠ADB+∠BDC=90°,
∴∠ADB=∠CDE,
∴△ADB∽△CDE.
(2)证明:过D点作DE⊥BD,交BC 的延长线于E点,
由(1)可得,△ADB∽△CDE,
∴,∠E=∠ABD=60°,
∵DE⊥BD,
∴∠BDE=90°,
∴∠DBE=30°,
∴BE=2DE,
∴,
∴,,
∴,BEBD,
,
即,
在等式两边都乘以,
∴;
(3)解:过D点作DE⊥BD,交BC 的延长线于E点,
由(1)可得,△ADB∽△CDE,
∴,
设DA=DB=1,则DC=DE,
∵∵DE⊥BD,
∴∠BDE=90°,
∴tan∠DBCk,
∴DE=DC=k,
过C作CF⊥DB于点F,设BF=x(0<x<1),
则DF=BD﹣BF=1﹣x,
在Rt△BFC中,tank,
∴CF=kx,
在Rt△DCF中,DF2+CF2=CD2,
∴(1﹣x)2+(kx)2=k2,
整理得(k2+1)x﹣2x+1﹣k2=0,
即[(k2+1)x﹣(1﹣k2)](x﹣1)=0,
解得x1,x2=1(舍去),
∴DF=1﹣x,
∴tan∠BDC.
12.【解答】(1)解:∵BD平分∠ABC,
∴∠ABEABC,
∵AE平分∠BAC,
∴∠BAEBAC,
∵∠AED=∠ABE+∠EBA,
∴∠AED(∠ABC+∠BAC).
∵∠ACB=70°,
∴∠ABC+∠BAC=180°﹣∠ACB=110°,
∴∠AED=55°,
∵AE⊥AD,
∴∠ADB=90°﹣∠AED=35°;
(2)证明:过点E作EF⊥BC于点F,EG⊥AB于点G,EH⊥AC于点H,连接CE,如图,
∵BD平分∠ABC,EF⊥BC,EG⊥AB,
∴EF=EG,
∵AE平分∠BAC,EH⊥AC,EG⊥AB,
∴EH=EG,
∴EF=EH,
∵EF⊥BC,EH⊥AC,
∴点E在∠ACB的平分线上,
∴∠ACEACB.
由(1)知:∠AED(∠ABC+∠BAC)=90°∠ACB,
∴∠AED=90°﹣∠ACE,
∵AE⊥AD,
∴∠ADB=90°﹣∠AED,
∴∠ACE=∠ADB,
∵∠EOC=∠AOD,
∴△EOC∽△AOD,
∴,
∵∠AOE=∠DOC,
∴△AOE∽△DOC;
(3)解:延长AE,交BC于点F,如图,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ADB=∠CBD,
∴AD∥BC,
∴△AED∽△FEB,
∴,
∵EDBD,
∴.
设AD=7k,则DF=4k,AB=AD=7k,
∵AE⊥AD,AD∥BC,
∴AF⊥BC,
∴sin∠BAF.
∵AE平分∠BAC,
∴∠CAE=∠BAF,
∴sin∠CAE=sin∠BAF.
13.【解答】(1)①证明:∵四边形ABCD为菱形,
∴∠ABD=∠GBF.
∵∠EAG=∠ABD,
∴∠EAG=∠GBF.
∵∠BFG=∠AFE,
∴△BFG∽△AFE,
∴∠AEB=∠BGF.
∵∠ABE=∠GBF,
∴△ABE∽△FBG;
②证明:连接EG,如图,
由(1)①得:△AFE∽△BFG,
∴.
∵∠EFG=∠AFB,
∴△AFB∽△EFG,
∴∠EGF=∠ABD.
∵∠EAG=∠ABD,
∴∠EAG=∠EGF,
∴EA=EG.
∵EH⊥AF,
∴AH=HG,
∴AG=2AH.
(2)解:连接FI,如图,
∵GI∥BF,GI=BF,
∴四边形BGIF为平行四边形.
∴FI∥BC,
∴.
∵四边形ABCD为菱形,
∴AD∥BC,
∴△ADF∽△GBF,
∴,
∴.
∵四边形ABCD为菱形,
∴AB=CD=BC=AD=2,
∴∠CBD=∠CDB,
∵GI∥BF,
∴∠CBD=∠CGI,∠CIG=∠CDB,
∴∠CGI=∠CIG,
∴CI=CG.
设CI=CG=x,则DI=BG=2﹣x,
∴,
解得:(不合题意,舍去),
即CI的长为.
14.【解答】(1)解:如图1中,连接AG,延长BE交AG于点J.
∵GE∥BC,
∴∠BCA=∠CEG=90°,
∴∠CAEG=90°,
由翻折变换的性质可知BE垂直平分线段AG,EG=EA,
∴∠GEJ=∠AEJ=45°,
∴∠BEC=45°;
(2)①解:设AE=EG=x,
∵BC∥EG,
∴∠CBH=∠EGH,
由翻折变换的性质可知∠BAE=∠BGE,
∴∠CBH=∠BAC,
∵∠BCH=∠BCA=90°,
∴△BCH∽∠ACB,
∴BC2=CH CA,
∴CH
∵CG∥AB,
∴∠GCH=∠CAB,
∴∠EGH=∠GCE,
∵∠GEH=∠GEC,
∴△GEH∽△CEG,
∴GE2=EH EC,
∴x2=(2)×2,
解得x1(负根已经舍去),
经检验x1是分式方程的解,
∴AE1,AC1,
∴;
②证明:
∵BC∥EG,
∴∠BCH=∠CEG,
∵∠CBH=∠A=∠BGE=∠ECG,CB=CE,
∴△CBH≌△ECG(ASA),
∴CH=GE=AE,
∵∠DCA+∠BCF=90°,∠CBH+∠BCF=90°,
∴∠DCA=∠CBH=∠A,
∴DC=DA,
∴△DHC≌△DEA(SAS),
∴DH=DE.
15.【解答】(1)证明:①∵四边形ABCD是矩形,EF⊥AE与直线CD交于点F,
∴∠B=∠C=90°,∠AEF=90°,
∴∠BAE+∠AEB=∠AEB+∠CEF,
∴∠BAE=∠CEF;
②∵EF⊥AE与直线CD交于点F,
∴∠AEF=∠B=∠C=90°,
∵由①得∠BAE=∠CEF,
∴△ABE∽△ECF,
∴,
在矩形ABCD中,E是BC的中点,
设AB=x、BE=CE=y、AE=a,
∵,
∴,
∴,
∴,,
∴且∠AEF=∠B=90°,
∴△AEF∽△ABE;
(2)解:①∵AD平分∠EAF,
∴∠FAD=∠DAE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AEB,
∴∠FAD=∠AEB,
∵∠FDA=∠B=90°,
∴△ABE∽△FDA,
设BE=EC=x,则AD=2x,
∴,
∴∠AFE=30°,
由(1)得△AEF∽△ABE,
∴∠AFE=∠AEB,
∴∠AFE=∠AEB=30°,
∴AE=2AB=4,
∴,
∴AF=8.
②;理由如下:
∵∠ECF=∠GDF=90°,∠CFE=∠DFG,
∴△ECF∽△GDF,
设AB=CD=x,BE=EC=y,
∵CG平分∠DCC′,
∴∠DCG=∠GCC′=45°,
∵AG∥BC′,
∴∠DGC=∠GCC′=45°,
∴DG=DC=x,
∴.
∵由(1)得△ABE∽△ECF,
∴,
∴,
∴,,
∵,
∴,
∴,
∴xy=x2﹣y2,
∴,
设,
∴t=1﹣t2,
解得:,(t2<0,舍去),
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
