人教版八年级数学下册期中模拟练习题(含答案)
文档属性
| 名称 | 人教版八年级数学下册期中模拟练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 13:36:53 | ||
图片预览




文档简介
八年级数学下册人教版期中模拟练习题
一、单选题
1.化简的结果是( )
A. B. C.2 D.
2.实数a,b在数轴上对应点A,B的位置如图,化简的结果是( )
A. B. C. D.
3.如图,在四边形中,,点是的中点,则的长为( )
A.2 B. C. D.3
4.如图,在菱形中,点、是、的中点,若,则菱形的周长为( )
A. B. C. D.
5.已知,,,…,,其中n为正整数.设,则值是( )
A. B. C. D.
6.如图,有一盏由传感器控制的灯,装在门上方离地面的墙上,任何东西只要移至该传感器周围及以内,灯就会自动发光,一位身高的学生要使灯刚好发光,则他与门的距离为( )
A. B. C. D.
7.如图,是一张纸片,,现将其折叠,使点与点重合,折痕为,则的长为( )
A. B.2 C. D.
8.如图,是的对角线,过点作交于点,垂足为,过点作交于点,垂足为,连接、.则下列结论:①;②四边形是平行四边形;③;④平分的周长;⑤.其中正确的个数是( )
A.2 B.3 C.4 D.5
9.如图,菱形的周长为40,面积为80,是对角线上一点,分别作点到直线,的垂线段,,则的值为( )
A.4 B.8 C.12 D.16
10.如图,长方形 中,,,点是边上一点,连接,把沿折叠,使点落在点处,若恰好为直角三角形,则的长为( )
A.1 B.3 C.1或 D.1或3
二、填空题
11.若在实数范围内有意义,则实数x的取值范围是 .
12.已知实数,满足,求的平方根 .
13.已知的整数部分为,小数部分为,则= .
14.如图,在中,,以点B为圆心,适当长为半径作弧,分别交,于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知,,则的长为 .
15.如图,点D,F把线段分成三条线段,分别以这三条线段为一条对角线作菱形,菱形,菱形,连结组成四边形.若菱形的边长为,,则四边形的面积是 .
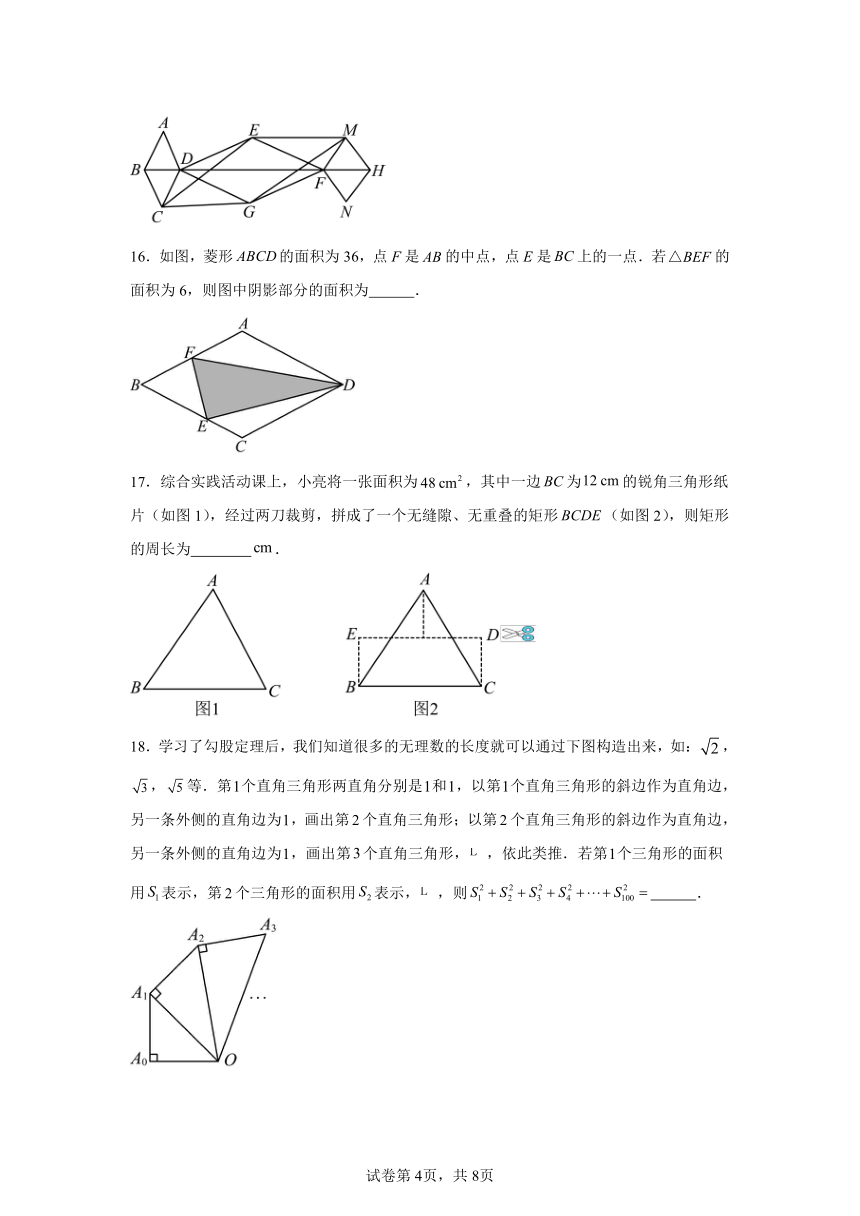
16.如图,菱形的面积为36,点F是的中点,点E是上的一点.若的面积为6,则图中阴影部分的面积为 .
17.综合实践活动课上,小亮将一张面积为,其中一边为的锐角三角形纸片(如图1),经过两刀裁剪,拼成了一个无缝隙、无重叠的矩形(如图2),则矩形的周长为 .
18.学习了勾股定理后,我们知道很多的无理数的长度就可以通过下图构造出来,如:,,等.第个直角三角形两直角分别是和,以第个直角三角形的斜边作为直角边,另一条外侧的直角边为,画出第个直角三角形;以第个直角三角形的斜边作为直角边,另一条外侧的直角边为,画出第个直角三角形,,依此类推.若第个三角形的面积用表示,第个三角形的面积用表示,,则 .
三、解答题
19.计算:
(1)
(2)
(3)
(4)
20.如图,在梯形中,,,过点作,垂足为,并延长至,使,联结、、.
(1)求证:四边形是平行四边形.
(2)联结,如果,,求证:四边形是矩形.
21.数学张老师在课堂上提出一个问题:“通过探究知道:,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
(1)的整数部分是______.
(2)a为的小数部分,b为的整数部分,求的值.
22.定义:在中,若,,,且a,b,c满足,则称这个三角形为“类勾股三角形”.
请根据以上定义解决下列问题:
(1)如图1,若等腰三角形是“类勾股三角形”,,,求的度数.
(2)如图2,在中,,且,D是AB上的点,连接CD,满足,过点作,垂足为.求证:为“类勾股三角形”.
23.我们学习了二次根式,那么所有的非负数都可以看成是一个数的平方,如,,下面我们观察:;反之,,,
(1)化简.
(2)化简.
(3)化简.
(4)若,则m,n与a,b的关系是什么?并说明理由.
24.如图,在某海域上,上午9时50分,缉私艇发现正东方向有一走私艇以16海里/时的速度偷偷沿方向行驶,便立即通知正在线上巡逻的缉私艇.已知A,C两艇之间的距离是10海里,A,B两艇之间的距离是6海里,B,C两艇之间的距离是8海里.若走私艇的速度不变,则它最早会在什么时间进入的西侧?
25.阅读材料:像,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式.在进行二次根式运算时,利用有理化因式可以化去分母中的根号.例如:
请你根据上述材料,解决如下问题:
(1)的有理化因式是______,______;
(2)比较大小:______(填>,<,或中的一种)
(3)计算:
26.如图,在平行四边形中,的平分线交于点,交的延长线于点,以、为邻边作平行四边形.
(1)证明:平行四边形是菱形;
(2)若,连接,,,
①求证:;
②求证:是等边三角形;
(3)若,,,是中点,求的长.
27.阅读与思考
【问题情境】教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?
【探索新知】从面积的角度思考;不难发现:大正方形的面积=小正方形的面积+4个直角三角形的面积,从而得数学等式:___________(用含字母、、式子表示),化简证得勾股定理:.
【初步运用】
(1)如图1,若,则小正方形面积:大正方形面积___________.
(2)现将图1中上方的两直角三角形向内折叠,如图2,,此时空白部分的面积为___________.
(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为,求该风车状图案的面积.
试卷第1页,共3页
试卷第1页,共3页
《八年级数学下册人教版期中模拟练习题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B A A A A C B C
11.且
12.
13.11
14.
15.
16.15
17.48
18.
19.(1)解:,
,
;
(2)解:,
,
,
,
;
(3)解:,
,
,
;
(4)解:,
,
.
20.(1)证明:连接.
梯形中,,,
,
和中,,,,
.
.
又,,
,,
,,
,
四边形是平行四边形;
(2)证明:垂直平分,
∴,,
,
∴
是等边三角形,
,,
∵,
∴,
,
∴
∵
,
四边形是平行四边形,
四边形是矩形
21.(1)解:,
的整数部分为3;
(2)解:为的小数部分,为的整数部分,
,,
.
22.(1)解:设,,,
∵ ABC是“类勾股三角形”,
∴,
∵,
∴,
∴,
∴,
∴ ABC是等腰直角三角形,
∴;
(2)证明:设,,,
∵,
∴,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
在中,,由勾股定理得,
在中,由勾股定理得,
∴,
∴,
∴ ABC为“类勾股三角形”.
23.(1)解:;
(2)解:;
(3)解:;
(4)解:
理由:把两边平方,得,
24.解:如图,设与相交于点,则.
,,
.
是直角三角形,且.
,
.
在中,由勾股定理,得.
(时)(分).
9时50分分时14分.
答:走私艇最早会在10时14分进入的西侧.
25.(1)解:的有理化因式是,
,
故答案为:;;
(2)解:∵,,
,
∴,
故答案为:;
(3)解:
.
26.(1)证明如下:
∵平分,
∴,
∵四边形平行四边形,
∴,,
∴,
∴,
∴,
∵四边形是平行四边形,
∴平行四边形是菱形.
(2)①证明如下:
∵四边形是平行四边形,
∴,,,
∵,
∴,,
由(1)得,四边形是菱形,
∴,,
∴是等边三角形,
∴,,
∴,
∵,
∴,
∴,
∵为的角平分线,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
②证明如下:∴,,
∴,
∵,
∴,
∴是等边三角形.
(3)解:连接,,,
∵,
∴四边形是矩形,
∴,
∴,
∵四边形是菱形,
∴四边形是正方形,
∵平分,
∴,
∴,
∵点为的中点,
∴,
∴,,
在和中
,
∴,
∴,,
∴,
∴是等腰直角三角形,
∵,,
∴,
∴;
27.解:【探索新知】由题意,大正方形面积为,小正方形面积为,四个直角三角形的面积为,
∴;
故答案为:;
【初步运用】(1)大正方形面积为,
小正方形面积为,
则,
故答案为:;
(2),一个直角三角形的面积为,
则空白部分面积为:;
故答案为:12;
(3)设,则,
由题意得,
∴,
即;
由勾股定理得:,
∵,
∴,
解得:,
∴,
故风车状图案的面积为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.化简的结果是( )
A. B. C.2 D.
2.实数a,b在数轴上对应点A,B的位置如图,化简的结果是( )
A. B. C. D.
3.如图,在四边形中,,点是的中点,则的长为( )
A.2 B. C. D.3
4.如图,在菱形中,点、是、的中点,若,则菱形的周长为( )
A. B. C. D.
5.已知,,,…,,其中n为正整数.设,则值是( )
A. B. C. D.
6.如图,有一盏由传感器控制的灯,装在门上方离地面的墙上,任何东西只要移至该传感器周围及以内,灯就会自动发光,一位身高的学生要使灯刚好发光,则他与门的距离为( )
A. B. C. D.
7.如图,是一张纸片,,现将其折叠,使点与点重合,折痕为,则的长为( )
A. B.2 C. D.
8.如图,是的对角线,过点作交于点,垂足为,过点作交于点,垂足为,连接、.则下列结论:①;②四边形是平行四边形;③;④平分的周长;⑤.其中正确的个数是( )
A.2 B.3 C.4 D.5
9.如图,菱形的周长为40,面积为80,是对角线上一点,分别作点到直线,的垂线段,,则的值为( )
A.4 B.8 C.12 D.16
10.如图,长方形 中,,,点是边上一点,连接,把沿折叠,使点落在点处,若恰好为直角三角形,则的长为( )
A.1 B.3 C.1或 D.1或3
二、填空题
11.若在实数范围内有意义,则实数x的取值范围是 .
12.已知实数,满足,求的平方根 .
13.已知的整数部分为,小数部分为,则= .
14.如图,在中,,以点B为圆心,适当长为半径作弧,分别交,于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知,,则的长为 .
15.如图,点D,F把线段分成三条线段,分别以这三条线段为一条对角线作菱形,菱形,菱形,连结组成四边形.若菱形的边长为,,则四边形的面积是 .
16.如图,菱形的面积为36,点F是的中点,点E是上的一点.若的面积为6,则图中阴影部分的面积为 .
17.综合实践活动课上,小亮将一张面积为,其中一边为的锐角三角形纸片(如图1),经过两刀裁剪,拼成了一个无缝隙、无重叠的矩形(如图2),则矩形的周长为 .
18.学习了勾股定理后,我们知道很多的无理数的长度就可以通过下图构造出来,如:,,等.第个直角三角形两直角分别是和,以第个直角三角形的斜边作为直角边,另一条外侧的直角边为,画出第个直角三角形;以第个直角三角形的斜边作为直角边,另一条外侧的直角边为,画出第个直角三角形,,依此类推.若第个三角形的面积用表示,第个三角形的面积用表示,,则 .
三、解答题
19.计算:
(1)
(2)
(3)
(4)
20.如图,在梯形中,,,过点作,垂足为,并延长至,使,联结、、.
(1)求证:四边形是平行四边形.
(2)联结,如果,,求证:四边形是矩形.
21.数学张老师在课堂上提出一个问题:“通过探究知道:,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
(1)的整数部分是______.
(2)a为的小数部分,b为的整数部分,求的值.
22.定义:在中,若,,,且a,b,c满足,则称这个三角形为“类勾股三角形”.
请根据以上定义解决下列问题:
(1)如图1,若等腰三角形是“类勾股三角形”,,,求的度数.
(2)如图2,在中,,且,D是AB上的点,连接CD,满足,过点作,垂足为.求证:为“类勾股三角形”.
23.我们学习了二次根式,那么所有的非负数都可以看成是一个数的平方,如,,下面我们观察:;反之,,,
(1)化简.
(2)化简.
(3)化简.
(4)若,则m,n与a,b的关系是什么?并说明理由.
24.如图,在某海域上,上午9时50分,缉私艇发现正东方向有一走私艇以16海里/时的速度偷偷沿方向行驶,便立即通知正在线上巡逻的缉私艇.已知A,C两艇之间的距离是10海里,A,B两艇之间的距离是6海里,B,C两艇之间的距离是8海里.若走私艇的速度不变,则它最早会在什么时间进入的西侧?
25.阅读材料:像,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式.在进行二次根式运算时,利用有理化因式可以化去分母中的根号.例如:
请你根据上述材料,解决如下问题:
(1)的有理化因式是______,______;
(2)比较大小:______(填>,<,或中的一种)
(3)计算:
26.如图,在平行四边形中,的平分线交于点,交的延长线于点,以、为邻边作平行四边形.
(1)证明:平行四边形是菱形;
(2)若,连接,,,
①求证:;
②求证:是等边三角形;
(3)若,,,是中点,求的长.
27.阅读与思考
【问题情境】教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?
【探索新知】从面积的角度思考;不难发现:大正方形的面积=小正方形的面积+4个直角三角形的面积,从而得数学等式:___________(用含字母、、式子表示),化简证得勾股定理:.
【初步运用】
(1)如图1,若,则小正方形面积:大正方形面积___________.
(2)现将图1中上方的两直角三角形向内折叠,如图2,,此时空白部分的面积为___________.
(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为,求该风车状图案的面积.
试卷第1页,共3页
试卷第1页,共3页
《八年级数学下册人教版期中模拟练习题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B A A A A C B C
11.且
12.
13.11
14.
15.
16.15
17.48
18.
19.(1)解:,
,
;
(2)解:,
,
,
,
;
(3)解:,
,
,
;
(4)解:,
,
.
20.(1)证明:连接.
梯形中,,,
,
和中,,,,
.
.
又,,
,,
,,
,
四边形是平行四边形;
(2)证明:垂直平分,
∴,,
,
∴
是等边三角形,
,,
∵,
∴,
,
∴
∵
,
四边形是平行四边形,
四边形是矩形
21.(1)解:,
的整数部分为3;
(2)解:为的小数部分,为的整数部分,
,,
.
22.(1)解:设,,,
∵ ABC是“类勾股三角形”,
∴,
∵,
∴,
∴,
∴,
∴ ABC是等腰直角三角形,
∴;
(2)证明:设,,,
∵,
∴,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
在中,,由勾股定理得,
在中,由勾股定理得,
∴,
∴,
∴ ABC为“类勾股三角形”.
23.(1)解:;
(2)解:;
(3)解:;
(4)解:
理由:把两边平方,得,
24.解:如图,设与相交于点,则.
,,
.
是直角三角形,且.
,
.
在中,由勾股定理,得.
(时)(分).
9时50分分时14分.
答:走私艇最早会在10时14分进入的西侧.
25.(1)解:的有理化因式是,
,
故答案为:;;
(2)解:∵,,
,
∴,
故答案为:;
(3)解:
.
26.(1)证明如下:
∵平分,
∴,
∵四边形平行四边形,
∴,,
∴,
∴,
∴,
∵四边形是平行四边形,
∴平行四边形是菱形.
(2)①证明如下:
∵四边形是平行四边形,
∴,,,
∵,
∴,,
由(1)得,四边形是菱形,
∴,,
∴是等边三角形,
∴,,
∴,
∵,
∴,
∴,
∵为的角平分线,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
②证明如下:∴,,
∴,
∵,
∴,
∴是等边三角形.
(3)解:连接,,,
∵,
∴四边形是矩形,
∴,
∴,
∵四边形是菱形,
∴四边形是正方形,
∵平分,
∴,
∴,
∵点为的中点,
∴,
∴,,
在和中
,
∴,
∴,,
∴,
∴是等腰直角三角形,
∵,,
∴,
∴;
27.解:【探索新知】由题意,大正方形面积为,小正方形面积为,四个直角三角形的面积为,
∴;
故答案为:;
【初步运用】(1)大正方形面积为,
小正方形面积为,
则,
故答案为:;
(2),一个直角三角形的面积为,
则空白部分面积为:;
故答案为:12;
(3)设,则,
由题意得,
∴,
即;
由勾股定理得:,
∵,
∴,
解得:,
∴,
故风车状图案的面积为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
