第十七章 勾股定理期中练习(含答案)
文档属性
| 名称 | 第十七章 勾股定理期中练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 458.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 15:13:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十七章勾股定理期中练习人教版2024—2025学年八年级下册
一、选择题
1.五根小木棒的长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,下列摆放正确的是( )
A. B. C. D.
2.如图,在一块四边形ABCD空地中植草皮,测得AB=3m,BC=4m,DA=13m,CD=12m,且∠ABC=90°.若每平方米草皮需要200元,则需要( )元投入.
A.16800 B.7200 C.5100 D.无法确定
3.已知:k>1,b=2k,a+c=2k2,ac=k4﹣1,则以a、b、c为边的三角形( )
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.形状无法确定
4.如图,已知圆柱的底面直径BC=,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )
A. B. C. D.
5.如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是( )
A. B.3 C.5 D.
6.若直角三角形的两边长为3和4,则第三边长为( )
A.5或 B. C.7 D.5
7.如图,数轴上的点A,点C表示的实数分别是﹣2,1,BC⊥AC于点C,且BC=1,连接AB.若以点A为圆心,AB长为半径画弧交数轴于点A右边的点P,则点P所表示的实数为( )
A. B. C. D.
8.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成.若AB=17,AH=8,则正方形EFGH的边长是( )
A.5 B.6 C.7 D.8
二、填空题
9.如图,Rt△ABC中,∠C=90°,BC>AC,以AB、BC、AC三边为边长的三个正方形面积分别为S1、S2、S3.若AB=5,S3=5,则S2的值等于 .
10.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了 米.
11.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.其中,b+a=12,则中间小正方形的面积是 .
12.一个三角形的三边长分别为5,12,13,则这个三角形最长边上的中线为 .
13.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为 cm(假设蜂蜜不会下滑).
三、解答题
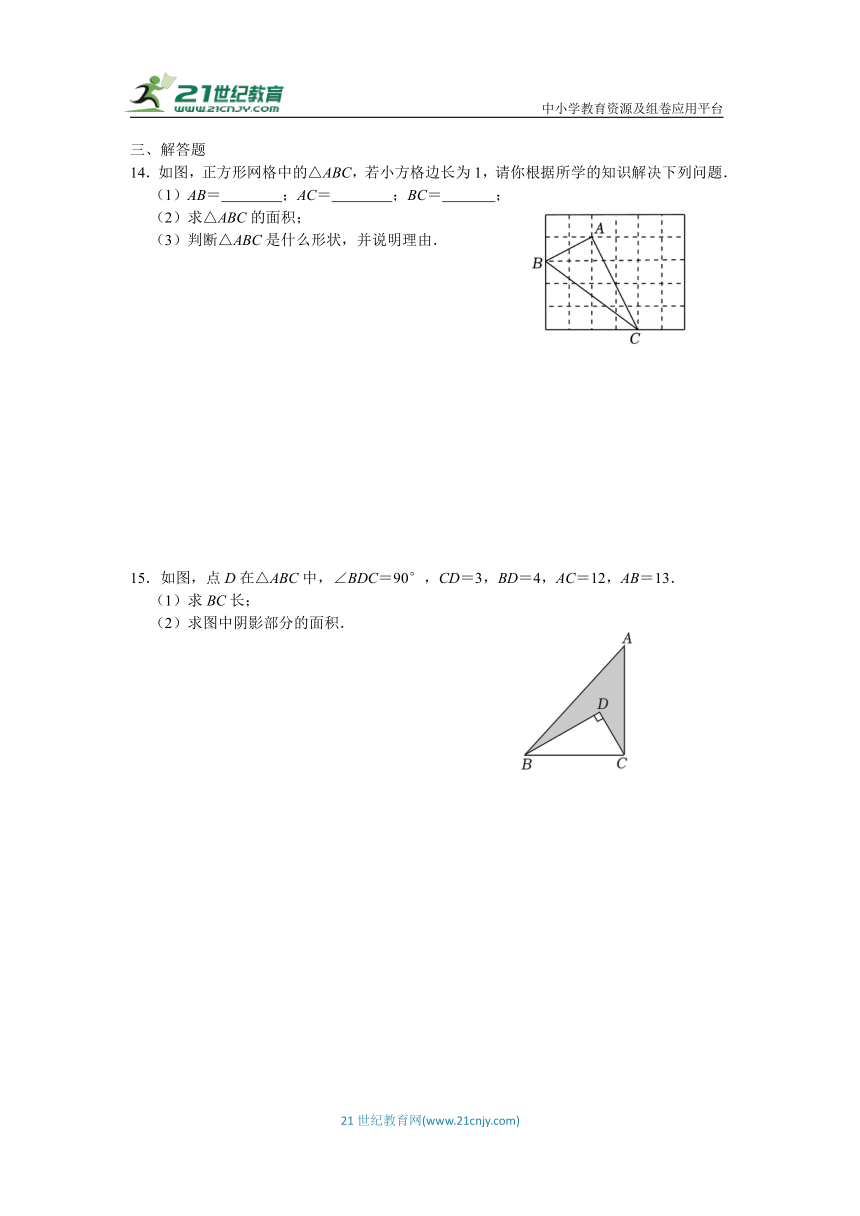
14.如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.
(1)AB= ;AC= ;BC= ;
(2)求△ABC的面积;
(3)判断△ABC是什么形状,并说明理由.
15.如图,点D在△ABC中,∠BDC=90°,CD=3,BD=4,AC=12,AB=13.
(1)求BC长;
(2)求图中阴影部分的面积.
16.全民健身手牵手,社区运动心连心.为提升社区居民的幸福感,某小区准备将辖区内的一块平地,如图所示的四边形ABCD进行改建,将四边形ABCD全部铺设具有耐磨性和防滑性的运动型塑胶地板.经测量,四边形ABCD中,∠B=90°,AB=24米,BC=7米,CD=15米,AD=20米.
(1)求AC的长度;
(2)已知运动型塑胶地板每平方米200元,请计算在四边形ABCD地面上全部铺设运动型塑胶地板,购买运动型塑胶地板的费用需要多少元?
17.如图,在△ABC中,AC=13cm,AB=12cm,BC=5cm,D是BC延长线上的点,连接AD,若AD=15cm.
(1)求CD的长;
(2)过点C作CE⊥AD交AD于点E,求CE的长.
18.如图,已知等腰△ABC中,AB=AC,BC=20cm,D是边AB上一点,且CD=16cm,BD=12cm.
(1)求AD的长;
(2)求△ABC中BC边上的高.
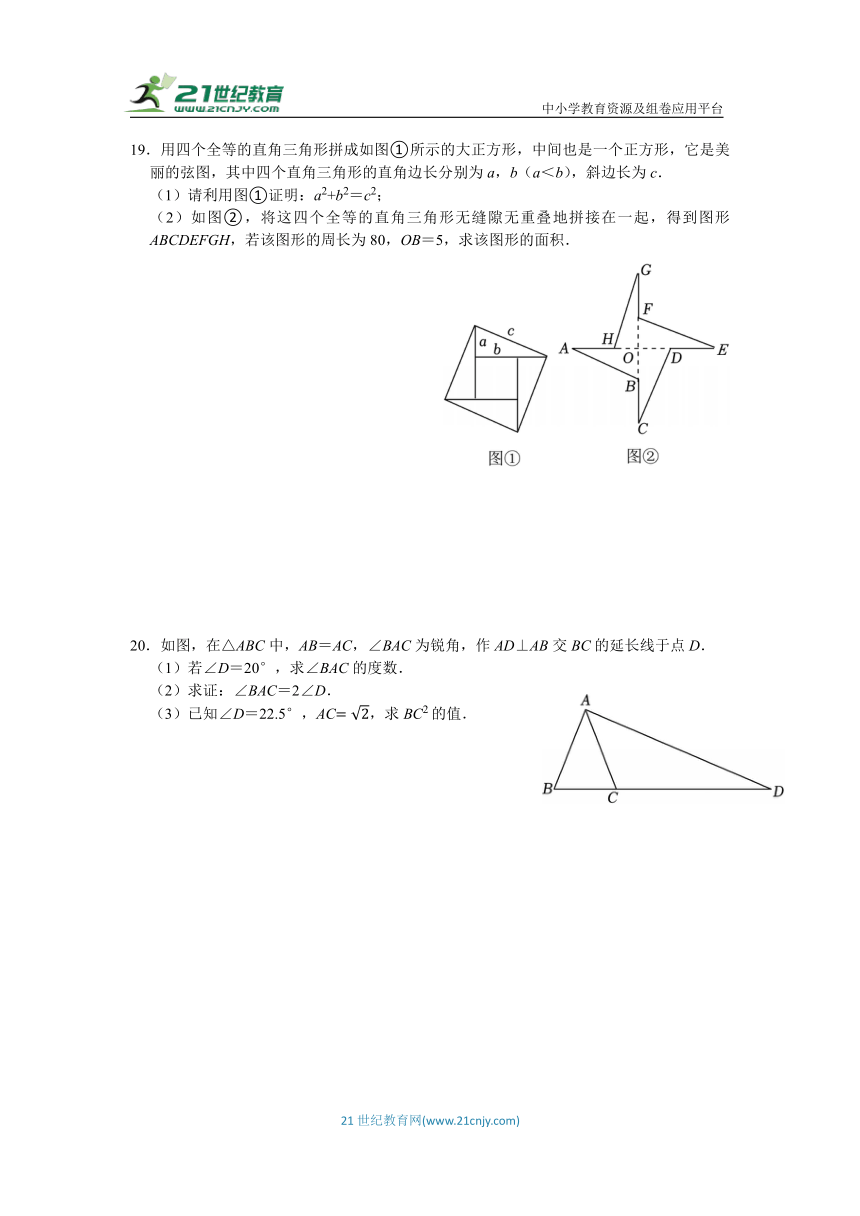
19.用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形,它是美丽的弦图,其中四个直角三角形的直角边长分别为a,b(a<b),斜边长为c.
(1)请利用图①证明:a2+b2=c2;
(2)如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,若该图形的周长为80,OB=5,求该图形的面积.
20.如图,在△ABC中,AB=AC,∠BAC为锐角,作AD⊥AB交BC的延长线于点D.
(1)若∠D=20°,求∠BAC的度数.
(2)求证:∠BAC=2∠D.
(3)已知∠D=22.5°,AC,求BC2的值.
参考答案
一、选择题
1.【解答】解:∵72=49,152=225,202=400,242=576,252=625,
∴72+242=252,152+202=252,
∴以7,24,25三根木棒能摆成直角三角形,以15,20,25三根木棒能摆成直角三角形,
故选:C.
2.【解答】解:连接AC,
因为AB=3m,BC=4m,DA=13m,CD=12m,∠B=90°,
所以AC2=AB2+BC2,
=42+32,
=16+9,
=25,
所以AC=5m,
又因AD2﹣DC2,
=132﹣122,
=169﹣144,
=25,
=AC2,
所以△DAC为直角三角形,
因此S四边形ABCD的面积=S△ABC+S△DAC,
AB×BCAD×AC,
4×312×5,
=6+30,
=36.
故费用为:200×36=7200元,
故选:B.
3.【解答】解:∵a+c=2k2,ac=k4﹣1,
∴a,c可以认为是x2﹣(2k2)x+k4﹣1=0的两根,
解得:x1=k2﹣1,x2=k2+1,
∵b=2k,
∴b2=4k2,
不妨令a=k2+1,c=k2﹣1
于是a2﹣c2=4k2=b2,
即a2=b2+c2,故为直角三角形.
故选:C.
4.【解答】解:把圆柱侧面展开,展开图如图所示,点A、C的最短距离为线段AC的长.
在RT△ADC中,∠ADC=90°,CD=AB=3,AD为底面半圆弧长,AD=3,
所以AC=3,
∴从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为2AC=6,
故选:D.
5.【解答】解:当沿前面和右面爬行时,将正方体展开,连接M、D1,
根据两点之间线段最短,
MD=MC+CD=1+2=3,
MD1===.
当沿前面和上面爬行时,MD1==,
<,
故选:A.
6.【解答】解:当长为4的边为直角边时,则第三边长为,
当长为4的边为斜边时,则第三边长为,
综上所述,第三边长为5或,
故选:A.
7.【解答】解:∵数轴上的点A,点C表示的实数分别是﹣2,1,
∴AC=1﹣(﹣2)=3,
在Rt△ABC中,由勾股定理得:AB,
∴点P表示的数为2,
故选:A.
8.【解答】解:由题意得,AD=AB=17,AH=DE=8,∠AHD=90°,
∴DH15,
∴HE=DH﹣DE=15﹣8=7,
∴正方形EFGH的边长是7,
故选:C.
二、填空题
9.【解答】解:由题意可得:AB2=52=25,
∵S3=5,
∴AC2=5,
BC2=AB2﹣AC2=20,
∴S2=20,
故答案为:20.
10.【解答】解:在Rt△ABC中:
∵∠CAB=90°,BC=17米,AC=8米,
∴AB15(米),
∵CD=10(米),
∴AD6(米),
∴BD=AB﹣AD=15﹣6=9(米),
答:船向岸边移动了9米,
故答案为:9.
11.【解答】解:由勾股定理,得a2+b2=c2=(3)2=90,
∵b+a=12,
∴b2+2ab+a2=144,
∴90+2ab=144,
∴ab=27,四个直角三角形的面积为4ab=54,
∴中间小正方形的面积是90﹣54=36.
故答案为:36.
12.【解答】解:∵三角形的三边长分别为5,12,13,符合勾股定理的逆定理52+122=132,
∴此三角形为直角三角形,则13为直角三角形的斜边,
∵三角形斜边上的中线是斜边的一半,
∴三角形最长边上的中线为.
故答案为:.
13.【解答】解:如图:
将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B===20(cm).
故答案为:20.
三、解答题
14.【解答】解:(1),,,
故答案为:;
(2)△ABC的面积=,
故答案为:5;
(3)∵,
∴△ABC是直角三角形.
15.【解答】解:(1)∵∠BDC=90°,BD=4,CD=3,
∴BC===5,
答:BC长是3;
(2)∵AB=13,AC=12,
∴AC2+BC2=122+52=144+25=169=132=AB2,
∴△ACB是直角三角形,∠ACB=90°,
∴S阴影=S△ACB﹣S△BDC=×5×12﹣×4×3=24.
故图中阴影部分的面积为24.
16.【解答】解:(1)在Rt△ABC中,由勾股定理得:AC25(米),
(2)∵152+202=625,252=625,
∴CD2+AD2=AC2,
∴△ACD为直角三角形,∠D=90°,
∴S四边形ABCD=S△ABC+S△ACDAB BCAD CD24×720×15=234(米2),
∴购买运动型塑胶地板的费用为:234×200=46800(元),
答:购买运动型塑胶地板的费用需要46800元.
17.【解答】解:(1)∵AC=13cm,AB=12cm,BC=5cm,
∴AC2=169,AB2=144,BC2=25,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,
∴∠ABD=90°,
在Rt△ABD中,由勾股定理得:,
∴CD=BD﹣BC=9﹣5=4(cm),
∴CD的长为4cm;
(2)由(1)得CD=4cm,∠ABD=90°,
∴AB⊥BD,
∵CE⊥AD,
∴,
∴,
∴15CE=48,
∴,
∴CE的长为cm.
18.【解答】解:(1)∵BC=20cm,且CD=16cm,BD=12cm,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=90°,
设AD=x cm,则AC=AB=(x+12)cm,
在Rt△ADC中,由勾股定理得:AD2+CD2=AC2,
即x2+162=(x+12)2,
解得:x=,
即AD=cm;
(2)AB=AC=+12=(cm),
过A作AE⊥BC于E,则AE是△ABC的高,
∵AB=AC,BC=20cm,
∴BE=CE=10(cm),
在Rt△AEB中,由勾股定理得:AE===(cm),
即△ABC中BC边上的高是cm.
19.【解答】(1)证明:S小正方形=(b﹣a)2=a2﹣2ab+b2,
S小正方形=c2﹣4ab=c2﹣2ab,
即b2﹣2ab+a2=c2﹣2ab,
∴a2+b2=c2;
(2)解:∵AB+BC=80÷4=20,
设AH=BC=x,则AB=20﹣x,OH=OB=5,
在Rt△AOB中,由勾股定理得:
OH2+OG2=GH2,
即52+(5+x)2=(20﹣x)2,
解得:x=7,
∴S5×12×4=120.
20.【解答】(1)解:∵AD⊥AB,
∴∠B+∠D=90°.
∵∠D=20°,
∴∠B=90°﹣20°=70°.
∵AB=AC,
∴∠ACB=∠B=70°,
∴∠BAC=180°﹣2×70°=40°.
(2)证明:∵AD⊥AB,
∴∠B+∠D=90°.,
即∠B=90°﹣∠D.
∵AB=AC,
∴∠B=∠ACB,
∴∠BAC=180°﹣2∠B,
即∠B=90°∠BAC,
∴90°﹣∠D=90°∠BAC,
∴∠BAC=2∠D.
(3)解:过点C作AB的垂线,垂足为M,
∵∠D=22.5°,
∴∠BAC=2×22.5°=45°,
∴△AMC是等腰直角三角形.
∵AC,
∴AM=MC=1.
∵AB=AC,
∴BM.
在Rt△BCM中,
BC2=BM2+MC2=()2+12=4.
21世纪教育网(www.21cnjy.com)
第十七章勾股定理期中练习人教版2024—2025学年八年级下册
一、选择题
1.五根小木棒的长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,下列摆放正确的是( )
A. B. C. D.
2.如图,在一块四边形ABCD空地中植草皮,测得AB=3m,BC=4m,DA=13m,CD=12m,且∠ABC=90°.若每平方米草皮需要200元,则需要( )元投入.
A.16800 B.7200 C.5100 D.无法确定
3.已知:k>1,b=2k,a+c=2k2,ac=k4﹣1,则以a、b、c为边的三角形( )
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.形状无法确定
4.如图,已知圆柱的底面直径BC=,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )
A. B. C. D.
5.如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是( )
A. B.3 C.5 D.
6.若直角三角形的两边长为3和4,则第三边长为( )
A.5或 B. C.7 D.5
7.如图,数轴上的点A,点C表示的实数分别是﹣2,1,BC⊥AC于点C,且BC=1,连接AB.若以点A为圆心,AB长为半径画弧交数轴于点A右边的点P,则点P所表示的实数为( )
A. B. C. D.
8.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成.若AB=17,AH=8,则正方形EFGH的边长是( )
A.5 B.6 C.7 D.8
二、填空题
9.如图,Rt△ABC中,∠C=90°,BC>AC,以AB、BC、AC三边为边长的三个正方形面积分别为S1、S2、S3.若AB=5,S3=5,则S2的值等于 .
10.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了 米.
11.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.其中,b+a=12,则中间小正方形的面积是 .
12.一个三角形的三边长分别为5,12,13,则这个三角形最长边上的中线为 .
13.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为 cm(假设蜂蜜不会下滑).
三、解答题
14.如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.
(1)AB= ;AC= ;BC= ;
(2)求△ABC的面积;
(3)判断△ABC是什么形状,并说明理由.
15.如图,点D在△ABC中,∠BDC=90°,CD=3,BD=4,AC=12,AB=13.
(1)求BC长;
(2)求图中阴影部分的面积.
16.全民健身手牵手,社区运动心连心.为提升社区居民的幸福感,某小区准备将辖区内的一块平地,如图所示的四边形ABCD进行改建,将四边形ABCD全部铺设具有耐磨性和防滑性的运动型塑胶地板.经测量,四边形ABCD中,∠B=90°,AB=24米,BC=7米,CD=15米,AD=20米.
(1)求AC的长度;
(2)已知运动型塑胶地板每平方米200元,请计算在四边形ABCD地面上全部铺设运动型塑胶地板,购买运动型塑胶地板的费用需要多少元?
17.如图,在△ABC中,AC=13cm,AB=12cm,BC=5cm,D是BC延长线上的点,连接AD,若AD=15cm.
(1)求CD的长;
(2)过点C作CE⊥AD交AD于点E,求CE的长.
18.如图,已知等腰△ABC中,AB=AC,BC=20cm,D是边AB上一点,且CD=16cm,BD=12cm.
(1)求AD的长;
(2)求△ABC中BC边上的高.
19.用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形,它是美丽的弦图,其中四个直角三角形的直角边长分别为a,b(a<b),斜边长为c.
(1)请利用图①证明:a2+b2=c2;
(2)如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,若该图形的周长为80,OB=5,求该图形的面积.
20.如图,在△ABC中,AB=AC,∠BAC为锐角,作AD⊥AB交BC的延长线于点D.
(1)若∠D=20°,求∠BAC的度数.
(2)求证:∠BAC=2∠D.
(3)已知∠D=22.5°,AC,求BC2的值.
参考答案
一、选择题
1.【解答】解:∵72=49,152=225,202=400,242=576,252=625,
∴72+242=252,152+202=252,
∴以7,24,25三根木棒能摆成直角三角形,以15,20,25三根木棒能摆成直角三角形,
故选:C.
2.【解答】解:连接AC,
因为AB=3m,BC=4m,DA=13m,CD=12m,∠B=90°,
所以AC2=AB2+BC2,
=42+32,
=16+9,
=25,
所以AC=5m,
又因AD2﹣DC2,
=132﹣122,
=169﹣144,
=25,
=AC2,
所以△DAC为直角三角形,
因此S四边形ABCD的面积=S△ABC+S△DAC,
AB×BCAD×AC,
4×312×5,
=6+30,
=36.
故费用为:200×36=7200元,
故选:B.
3.【解答】解:∵a+c=2k2,ac=k4﹣1,
∴a,c可以认为是x2﹣(2k2)x+k4﹣1=0的两根,
解得:x1=k2﹣1,x2=k2+1,
∵b=2k,
∴b2=4k2,
不妨令a=k2+1,c=k2﹣1
于是a2﹣c2=4k2=b2,
即a2=b2+c2,故为直角三角形.
故选:C.
4.【解答】解:把圆柱侧面展开,展开图如图所示,点A、C的最短距离为线段AC的长.
在RT△ADC中,∠ADC=90°,CD=AB=3,AD为底面半圆弧长,AD=3,
所以AC=3,
∴从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为2AC=6,
故选:D.
5.【解答】解:当沿前面和右面爬行时,将正方体展开,连接M、D1,
根据两点之间线段最短,
MD=MC+CD=1+2=3,
MD1===.
当沿前面和上面爬行时,MD1==,
<,
故选:A.
6.【解答】解:当长为4的边为直角边时,则第三边长为,
当长为4的边为斜边时,则第三边长为,
综上所述,第三边长为5或,
故选:A.
7.【解答】解:∵数轴上的点A,点C表示的实数分别是﹣2,1,
∴AC=1﹣(﹣2)=3,
在Rt△ABC中,由勾股定理得:AB,
∴点P表示的数为2,
故选:A.
8.【解答】解:由题意得,AD=AB=17,AH=DE=8,∠AHD=90°,
∴DH15,
∴HE=DH﹣DE=15﹣8=7,
∴正方形EFGH的边长是7,
故选:C.
二、填空题
9.【解答】解:由题意可得:AB2=52=25,
∵S3=5,
∴AC2=5,
BC2=AB2﹣AC2=20,
∴S2=20,
故答案为:20.
10.【解答】解:在Rt△ABC中:
∵∠CAB=90°,BC=17米,AC=8米,
∴AB15(米),
∵CD=10(米),
∴AD6(米),
∴BD=AB﹣AD=15﹣6=9(米),
答:船向岸边移动了9米,
故答案为:9.
11.【解答】解:由勾股定理,得a2+b2=c2=(3)2=90,
∵b+a=12,
∴b2+2ab+a2=144,
∴90+2ab=144,
∴ab=27,四个直角三角形的面积为4ab=54,
∴中间小正方形的面积是90﹣54=36.
故答案为:36.
12.【解答】解:∵三角形的三边长分别为5,12,13,符合勾股定理的逆定理52+122=132,
∴此三角形为直角三角形,则13为直角三角形的斜边,
∵三角形斜边上的中线是斜边的一半,
∴三角形最长边上的中线为.
故答案为:.
13.【解答】解:如图:
将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B===20(cm).
故答案为:20.
三、解答题
14.【解答】解:(1),,,
故答案为:;
(2)△ABC的面积=,
故答案为:5;
(3)∵,
∴△ABC是直角三角形.
15.【解答】解:(1)∵∠BDC=90°,BD=4,CD=3,
∴BC===5,
答:BC长是3;
(2)∵AB=13,AC=12,
∴AC2+BC2=122+52=144+25=169=132=AB2,
∴△ACB是直角三角形,∠ACB=90°,
∴S阴影=S△ACB﹣S△BDC=×5×12﹣×4×3=24.
故图中阴影部分的面积为24.
16.【解答】解:(1)在Rt△ABC中,由勾股定理得:AC25(米),
(2)∵152+202=625,252=625,
∴CD2+AD2=AC2,
∴△ACD为直角三角形,∠D=90°,
∴S四边形ABCD=S△ABC+S△ACDAB BCAD CD24×720×15=234(米2),
∴购买运动型塑胶地板的费用为:234×200=46800(元),
答:购买运动型塑胶地板的费用需要46800元.
17.【解答】解:(1)∵AC=13cm,AB=12cm,BC=5cm,
∴AC2=169,AB2=144,BC2=25,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,
∴∠ABD=90°,
在Rt△ABD中,由勾股定理得:,
∴CD=BD﹣BC=9﹣5=4(cm),
∴CD的长为4cm;
(2)由(1)得CD=4cm,∠ABD=90°,
∴AB⊥BD,
∵CE⊥AD,
∴,
∴,
∴15CE=48,
∴,
∴CE的长为cm.
18.【解答】解:(1)∵BC=20cm,且CD=16cm,BD=12cm,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=90°,
设AD=x cm,则AC=AB=(x+12)cm,
在Rt△ADC中,由勾股定理得:AD2+CD2=AC2,
即x2+162=(x+12)2,
解得:x=,
即AD=cm;
(2)AB=AC=+12=(cm),
过A作AE⊥BC于E,则AE是△ABC的高,
∵AB=AC,BC=20cm,
∴BE=CE=10(cm),
在Rt△AEB中,由勾股定理得:AE===(cm),
即△ABC中BC边上的高是cm.
19.【解答】(1)证明:S小正方形=(b﹣a)2=a2﹣2ab+b2,
S小正方形=c2﹣4ab=c2﹣2ab,
即b2﹣2ab+a2=c2﹣2ab,
∴a2+b2=c2;
(2)解:∵AB+BC=80÷4=20,
设AH=BC=x,则AB=20﹣x,OH=OB=5,
在Rt△AOB中,由勾股定理得:
OH2+OG2=GH2,
即52+(5+x)2=(20﹣x)2,
解得:x=7,
∴S5×12×4=120.
20.【解答】(1)解:∵AD⊥AB,
∴∠B+∠D=90°.
∵∠D=20°,
∴∠B=90°﹣20°=70°.
∵AB=AC,
∴∠ACB=∠B=70°,
∴∠BAC=180°﹣2×70°=40°.
(2)证明:∵AD⊥AB,
∴∠B+∠D=90°.,
即∠B=90°﹣∠D.
∵AB=AC,
∴∠B=∠ACB,
∴∠BAC=180°﹣2∠B,
即∠B=90°∠BAC,
∴90°﹣∠D=90°∠BAC,
∴∠BAC=2∠D.
(3)解:过点C作AB的垂线,垂足为M,
∵∠D=22.5°,
∴∠BAC=2×22.5°=45°,
∴△AMC是等腰直角三角形.
∵AC,
∴AM=MC=1.
∵AB=AC,
∴BM.
在Rt△BCM中,
BC2=BM2+MC2=()2+12=4.
21世纪教育网(www.21cnjy.com)
同课章节目录
