人教版九年级数学下册4月期中模拟练习题(含答案)
文档属性
| 名称 | 人教版九年级数学下册4月期中模拟练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 00:00:00 | ||
图片预览

文档简介
九年级数学下册人教版4月期中模拟练习题
一、单选题
1.在平面直角坐标系中,,双曲线上一点P,以点P为圆心的过两点且与y轴相切,则k的值为( )
A.12 B. C. D.
2.如图,一次函数与反比例函数交于C、D两点,,则k的值为( )
A. B. C. D.
3.小明喜欢用计算机软件研究数学问题,下图是他绘制的“对勾”函数的图象,发现它关于原点中心对称.下面是关于函数的描述,其中正确的是( )
A.函数图象的对称中心是
B.当时,随的增大而增大
C.当时,函数有最小值,且最小值为4
D.二次函数的图象与函数的图象有3个不同的公共点
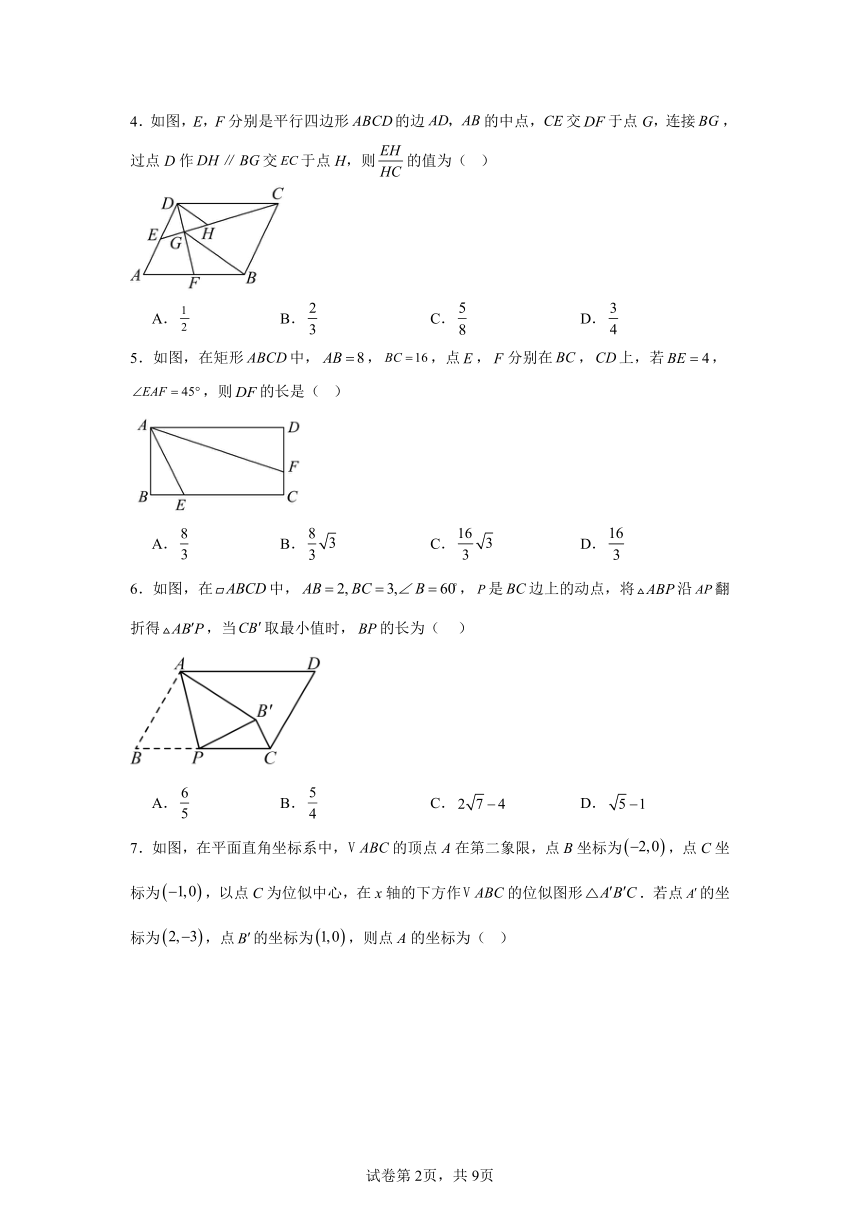
4.如图,E,F分别是平行四边形的边的中点,交于点G,连接,过点D作交于点H,则的值为( )
A. B. C. D.
5.如图,在矩形中,,,点,分别在,上,若,,则的长是( )
A. B. C. D.
6.如图,在中,,是边上的动点,将沿翻折得,当取最小值时,的长为( )
A. B. C. D.
7.如图,在平面直角坐标系中,的顶点A在第二象限,点B坐标为,点C坐标为,以点C为位似中心,在x轴的下方作的位似图形.若点的坐标为,点的坐标为,则点A的坐标为( )
A. B. C. D.
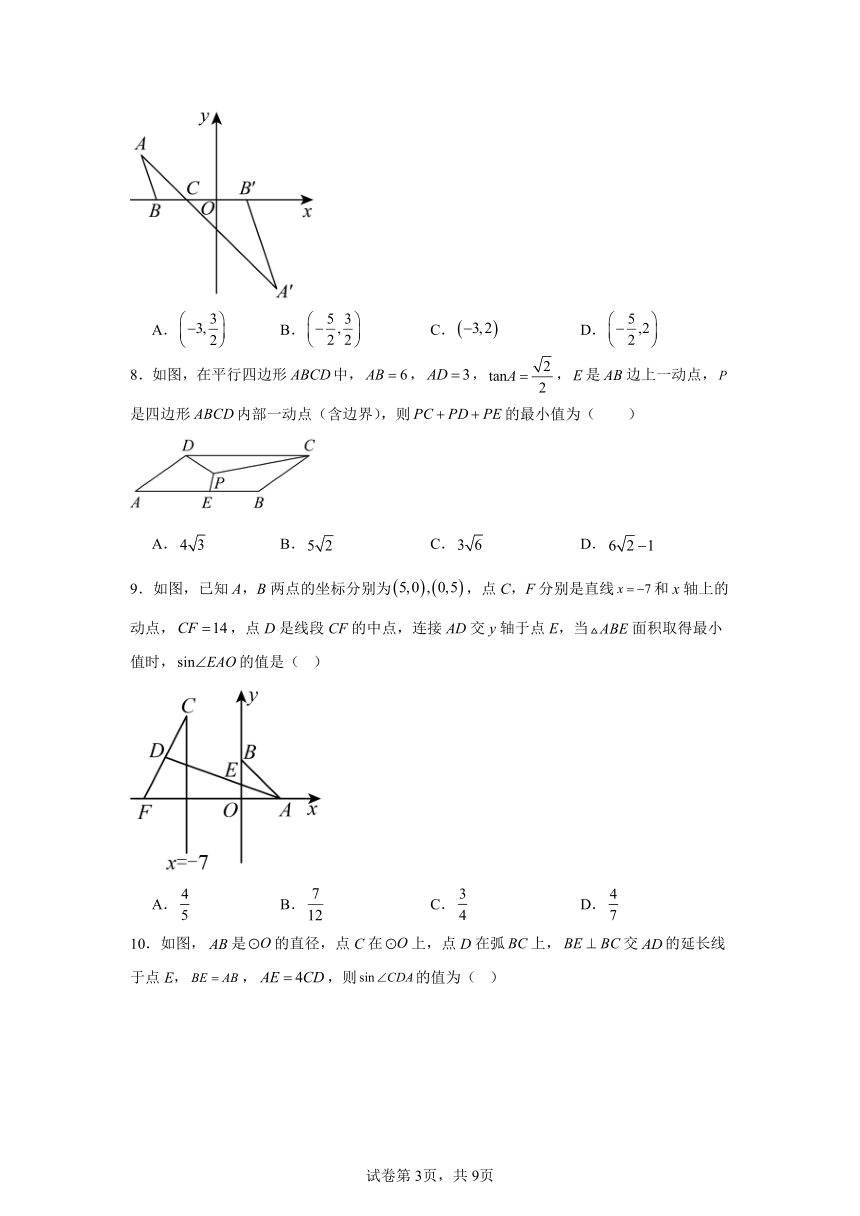
8.如图,在平行四边形中,,,,是边上一动点,是四边形内部一动点(含边界),则的最小值为( )
A. B. C. D.
9.如图,已知A,B两点的坐标分别为,点C,F分别是直线和x轴上的动点,,点D是线段CF的中点,连接AD交y轴于点E,当面积取得最小值时,的值是( )
A. B. C. D.
10.如图,是的直径,点C在上,点D在弧上,交的延长线于点E,,,则的值为( )
A. B. C. D.
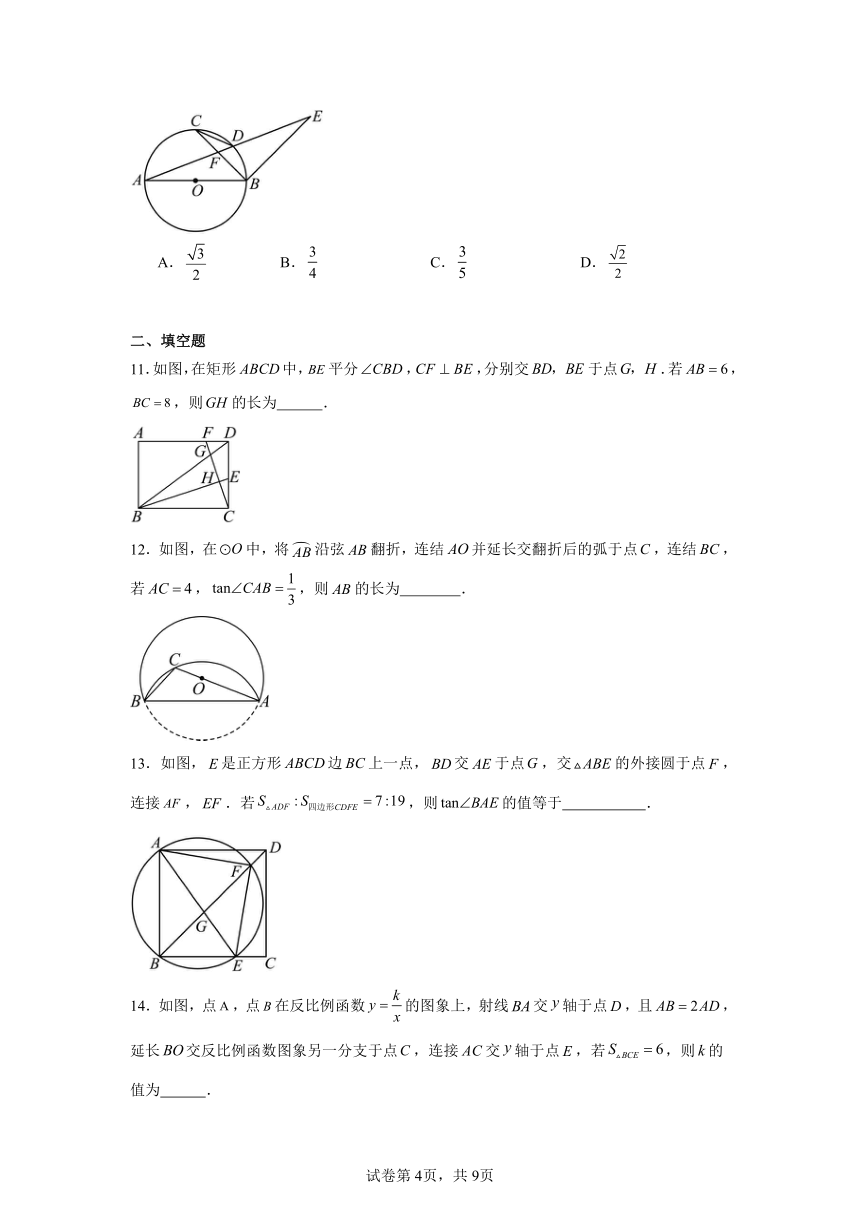
二、填空题
11.如图,在矩形中,平分,,分别交于点.若,,则的长为 .
12.如图,在中,将沿弦翻折,连结并延长交翻折后的弧于点,连结,若,,则的长为 .
13.如图,是正方形边上一点,交于点,交的外接圆于点,连接,.若,则的值等于 .
14.如图,点,点在反比例函数的图象上,射线交轴于点,且,延长交反比例函数图象另一分支于点,连接交轴于点,若,则的值为 .
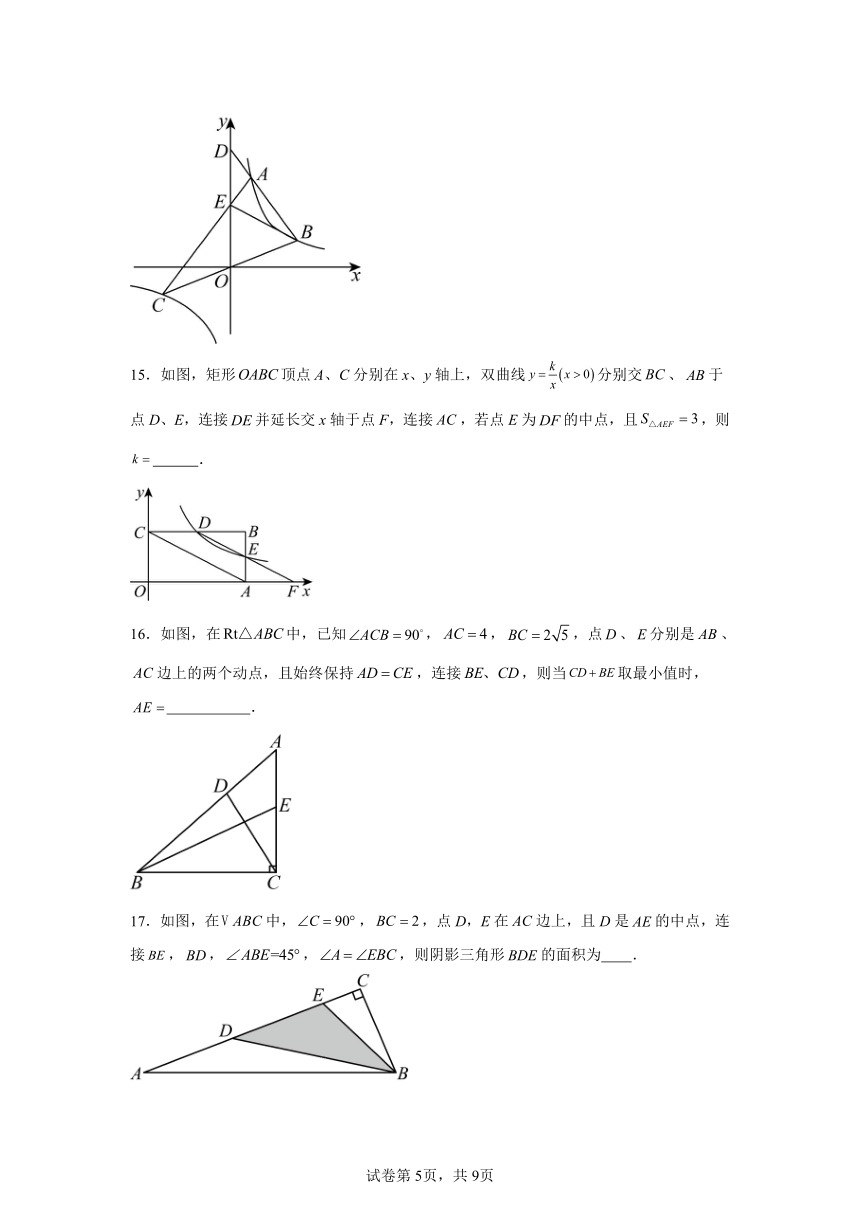
15.如图,矩形顶点A、C分别在x、y轴上,双曲线分别交、于点D、E,连接并延长交x轴于点F,连接,若点E为的中点,且,则 .
16.如图,在中,已知,,,点、分别是、边上的两个动点,且始终保持,连接,则当取最小值时, .
17.如图,在中,,,点D,E在边上,且D是的中点,连接,,,,则阴影三角形的面积为 .
18.如图,矩形在平面直角坐标系中,点B的坐标是,过点A作,交x轴于,过点作轴交直线于,过点作直线,交x轴于,过点作轴交直线于,……,则 ,的坐标是 .
三、解答题
19.(1)计算:
(2)先化简,再求值: ,其中
20.如图,在平面直角坐标系内,函数的图象与反比例函数图象有公共点,点的坐标为,轴,垂足为点.
(1)求反比例函数的解析式;
(2)点在线段上,若,求线段的长;
(3)点C为轴正半轴上一点,若是以为腰的等腰三角形,请直接写出点C坐标.
21.如图,在平行四边形 中,过 三点的 交 于点 ,连结 .
(1)求证: .
(2)如图 2 ,已知 为 的切线,连结 并延长交 于点 .
①求证: ;
②若 ,求 的值.
22.如图1,在中,,,点D在边上,连接,作交线段于点E.
(1)求证:;
(2)如图2,连接,若,求证:;
(3)如图3,若,求的面积.
23.如图,已知在中,,点是上一点,把沿着对折得到,,连接.
(1)求的度数.
(2)若.
①如图1,若,求的值;
②如图2,过点作的垂线分别交于点,连接.求证:.
24.已知点是矩形边延长上一点,且,是对角线和的交点.连接,交于,交于,连接,如图1.
(1)求证:平分.
(2)若,,求的值.
(3)若,如图2,求的值.
25.【概念感知】
如果线段与函数图象只有一个公共点,我们称线段与这个函数图象一点相交.
【概念理解】
(1)我们知道正比例函数的图象是一条经过原点的直线,当限定自变量的取值范围为时,即可得到一条线段,如果这条线段与函数的图象一点相交,则的取值范围是 ;
【概念应用】
(2)如图1,抛物线(为常数且)顶点为,交轴于点,其对称轴与双曲线交于点.
①连接,,当时,求抛物线的解析式;
②连接,当线段与抛物线一点相交时,求的取值范围.
26.【问题思考】
(1)如图1,已知正方形,,分别是边,上一点,连接,,,且,若延长到,使得,连接.
则:运用三角形全等的相关知识,可推理得到三条线段,,之间的数量关系是 .
【探究应用】
(2)如图2,正方形的边长为,点是射线上一动点(不与点重合),连接,以为边长在的上方作正方形,交射线于点,连接.
①当点E在上时.
(ⅰ)若,求的值;
(ⅱ)若是等腰三角形,求此时的长.
②点在的延长线上时,若,则线段的长为______.
27.如图,有两个长度相同的滑梯(即),左边滑梯的高度与右边滑梯水平方向的长度相等.
(1)求证:;
(2)若滑梯的长度米,米,分别求出滑梯与的坡度;
(3)在(2)的条件下,由于太陡,在保持.长不变的情况下,现在将点沿方向,向下移动,点随之向右移动.在移动的过程中,直接写出面积的最大值.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册人教版4月期中模拟练习题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B D C B A B C
11.
12./
13.
14.3
15.
16.
17.2
18.
19.解:(1)原式
.
(2)原式
.
当时,原式.
20.(1)解:∵函数的图象过点,
∴,
∴点A的坐标为,
∵反比例函数图象过点,
∴,
解得,
∴反比例函数的解析式为;
(2)解:设,则,
∵点,轴于点B,
∴,,,
∴,
解得,,
∴,
即线段的长是5;
(3)解:是以为腰的等腰三角形,分以下两种情况:
当时,如图,
∵点,
∴,
∴,
∴;
当时,如图,
∵轴于点B,
∴,,
∴.
综上,点C的坐标为或.
21.(1)证明:
.
,
;
(2)①证明:如图,延长 交 于点 ,连结 ,
切 于点,
,
∵,
∴
,
∴,
∴.
∵,
∴,
∴,
∴,
即.
②如图3,延长交的延长线于点M,设,则.
由,
∴,
∴.
由,得,
,
解得.
由 得.
∵,
∴,
∴ .
∴,
∴,
∴.
∵,且,
∴,
∴.
设,则,得 ,
解得,
∴,
∴.
22.(1)证明:∵,
又∵,
∴,
∵,
∴,
∴;
(2)在上截取,由(1)知:,
又∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴;
(3)∵,
∴,
过点作于点,则:,
由(1)知:,
∴,
∴,
∴,
∵,
∴,
∴为等腰直角三角形,
∴,
∴,
∴,
∴在中,,
∴,
∴,
∴,
∴
.
23.(1)解:∵折叠,
∴,
∵,
∴,
∴,
∵,
∴,且,
∴,即;
(2)解:①由(1)可得,,
∴,
设,则,
∵,,
∴,,
∴,
∴,即,
整理得,,
解得,,
∴(负值舍去),
∴,
∴;
②由折叠的性质得,
∵,,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
∴
∵,
∴,
∴,
∵,
∴,
∴,
∴,
由①知,
∴,即,
∴,
∴,
∵
∴,
∴.
24.(1)证明:∵矩形,
∴,
,
,
平分.
(2)过作于.
在矩形中,,,
,,
,,
由(1)得平分,
,
,
,
又,
,
,
∵,,
∴,
,
,
;
(3),
矩形是正方形,
设,则,
由(2)知:,
,,
∴,
,平分,
∴,
,
,
,
.
25.(1)解:当限定自变量的取值范围为时,
则,
如果这条线段与函数的图象一点相交,
则反比例函数与直线的最右交点为,代入反比例函数可得,
反比例函数与直线的最左交点为,代入反比例函数可得,
(2)①解:∵,
∴抛物线的顶点,
将,代入得,
∴,
∴,,
如图,过点作垂足为,交轴于点,
则四边形为矩形,当时,与不平行
∴,
∵,,
∴,
∴,
∵,
∴,解得
∴抛物线的解析式为
如图,当时,过点作轴,垂足为,交轴于点,
则四边形为矩形,同理可得,
,
,
∴解得
∴抛物线的解析式为
综上所述,抛物线的解析式为或
②解:如图,当时,若线段与抛物线一点相交,则点与点重合或点在点下方,
∴,
∴或,
∵,
∴
如图,当,且点在点的下方时,若线段与抛物线一点相交,则点与点重合或点在点下方,
∴,
∴或,
∵,
∴,
如图,当,且点在点的上方时,则线段与抛物线一点相交,此时解得,
∵,
∴,
综上所述,当或或时,线段与抛物线一点相交.
26.解:(1),之间的数量关系是:.理由:
四边形为正方形,
,,
在和中,
,
,
,,
,
,
即.
,
.
在和中,
,
,
,
,
.
故答案为:;
(2)①(i)连接,如图,
四边形为正方形,
,,
,
由()知:.
正方形的边长为,,
.
设,则,.
,
,
.
,
;
(ii)过点作,交的延长线于点,如图,
四边形和四边形为正方形,
,,,
,,
,
在和中,
,
,
,,
,
,
,
为等腰直角三角形,
.
设,则,,.
.
Ⅰ.当时,,
.
,
.
此时,不合题意,舍去;
Ⅱ.当时,,
,
此时,点与点重合,
点与点重合,
;
Ⅲ.当时,.
则,
.
,
.
解得:
综上,若是等腰三角形,的长为或;
②过点作,交的延长线于点,延长,交于点,如图,
四边形和四边形为正方形,
,,,
,,
,
在和中,
,
,
,,
,
四边形为矩形,
,,
同理:四边形为矩形,
.
,
.
设,则,
.
,
.
,,
,
,
,
,
,
,
.
故答案为:.
27.(1)在与中,
,
∴;
(2)∵,
∴米.
在中,(米),
∴米,
∴滑梯的坡度为.
滑梯的坡度为;
(3)设点E向下滑动的距离为x米,则此时米
在中,,
当时,面积的最大,,
解得:,
∴面积最大值为平方米.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在平面直角坐标系中,,双曲线上一点P,以点P为圆心的过两点且与y轴相切,则k的值为( )
A.12 B. C. D.
2.如图,一次函数与反比例函数交于C、D两点,,则k的值为( )
A. B. C. D.
3.小明喜欢用计算机软件研究数学问题,下图是他绘制的“对勾”函数的图象,发现它关于原点中心对称.下面是关于函数的描述,其中正确的是( )
A.函数图象的对称中心是
B.当时,随的增大而增大
C.当时,函数有最小值,且最小值为4
D.二次函数的图象与函数的图象有3个不同的公共点
4.如图,E,F分别是平行四边形的边的中点,交于点G,连接,过点D作交于点H,则的值为( )
A. B. C. D.
5.如图,在矩形中,,,点,分别在,上,若,,则的长是( )
A. B. C. D.
6.如图,在中,,是边上的动点,将沿翻折得,当取最小值时,的长为( )
A. B. C. D.
7.如图,在平面直角坐标系中,的顶点A在第二象限,点B坐标为,点C坐标为,以点C为位似中心,在x轴的下方作的位似图形.若点的坐标为,点的坐标为,则点A的坐标为( )
A. B. C. D.
8.如图,在平行四边形中,,,,是边上一动点,是四边形内部一动点(含边界),则的最小值为( )
A. B. C. D.
9.如图,已知A,B两点的坐标分别为,点C,F分别是直线和x轴上的动点,,点D是线段CF的中点,连接AD交y轴于点E,当面积取得最小值时,的值是( )
A. B. C. D.
10.如图,是的直径,点C在上,点D在弧上,交的延长线于点E,,,则的值为( )
A. B. C. D.
二、填空题
11.如图,在矩形中,平分,,分别交于点.若,,则的长为 .
12.如图,在中,将沿弦翻折,连结并延长交翻折后的弧于点,连结,若,,则的长为 .
13.如图,是正方形边上一点,交于点,交的外接圆于点,连接,.若,则的值等于 .
14.如图,点,点在反比例函数的图象上,射线交轴于点,且,延长交反比例函数图象另一分支于点,连接交轴于点,若,则的值为 .
15.如图,矩形顶点A、C分别在x、y轴上,双曲线分别交、于点D、E,连接并延长交x轴于点F,连接,若点E为的中点,且,则 .
16.如图,在中,已知,,,点、分别是、边上的两个动点,且始终保持,连接,则当取最小值时, .
17.如图,在中,,,点D,E在边上,且D是的中点,连接,,,,则阴影三角形的面积为 .
18.如图,矩形在平面直角坐标系中,点B的坐标是,过点A作,交x轴于,过点作轴交直线于,过点作直线,交x轴于,过点作轴交直线于,……,则 ,的坐标是 .
三、解答题
19.(1)计算:
(2)先化简,再求值: ,其中
20.如图,在平面直角坐标系内,函数的图象与反比例函数图象有公共点,点的坐标为,轴,垂足为点.
(1)求反比例函数的解析式;
(2)点在线段上,若,求线段的长;
(3)点C为轴正半轴上一点,若是以为腰的等腰三角形,请直接写出点C坐标.
21.如图,在平行四边形 中,过 三点的 交 于点 ,连结 .
(1)求证: .
(2)如图 2 ,已知 为 的切线,连结 并延长交 于点 .
①求证: ;
②若 ,求 的值.
22.如图1,在中,,,点D在边上,连接,作交线段于点E.
(1)求证:;
(2)如图2,连接,若,求证:;
(3)如图3,若,求的面积.
23.如图,已知在中,,点是上一点,把沿着对折得到,,连接.
(1)求的度数.
(2)若.
①如图1,若,求的值;
②如图2,过点作的垂线分别交于点,连接.求证:.
24.已知点是矩形边延长上一点,且,是对角线和的交点.连接,交于,交于,连接,如图1.
(1)求证:平分.
(2)若,,求的值.
(3)若,如图2,求的值.
25.【概念感知】
如果线段与函数图象只有一个公共点,我们称线段与这个函数图象一点相交.
【概念理解】
(1)我们知道正比例函数的图象是一条经过原点的直线,当限定自变量的取值范围为时,即可得到一条线段,如果这条线段与函数的图象一点相交,则的取值范围是 ;
【概念应用】
(2)如图1,抛物线(为常数且)顶点为,交轴于点,其对称轴与双曲线交于点.
①连接,,当时,求抛物线的解析式;
②连接,当线段与抛物线一点相交时,求的取值范围.
26.【问题思考】
(1)如图1,已知正方形,,分别是边,上一点,连接,,,且,若延长到,使得,连接.
则:运用三角形全等的相关知识,可推理得到三条线段,,之间的数量关系是 .
【探究应用】
(2)如图2,正方形的边长为,点是射线上一动点(不与点重合),连接,以为边长在的上方作正方形,交射线于点,连接.
①当点E在上时.
(ⅰ)若,求的值;
(ⅱ)若是等腰三角形,求此时的长.
②点在的延长线上时,若,则线段的长为______.
27.如图,有两个长度相同的滑梯(即),左边滑梯的高度与右边滑梯水平方向的长度相等.
(1)求证:;
(2)若滑梯的长度米,米,分别求出滑梯与的坡度;
(3)在(2)的条件下,由于太陡,在保持.长不变的情况下,现在将点沿方向,向下移动,点随之向右移动.在移动的过程中,直接写出面积的最大值.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册人教版4月期中模拟练习题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B D C B A B C
11.
12./
13.
14.3
15.
16.
17.2
18.
19.解:(1)原式
.
(2)原式
.
当时,原式.
20.(1)解:∵函数的图象过点,
∴,
∴点A的坐标为,
∵反比例函数图象过点,
∴,
解得,
∴反比例函数的解析式为;
(2)解:设,则,
∵点,轴于点B,
∴,,,
∴,
解得,,
∴,
即线段的长是5;
(3)解:是以为腰的等腰三角形,分以下两种情况:
当时,如图,
∵点,
∴,
∴,
∴;
当时,如图,
∵轴于点B,
∴,,
∴.
综上,点C的坐标为或.
21.(1)证明:
.
,
;
(2)①证明:如图,延长 交 于点 ,连结 ,
切 于点,
,
∵,
∴
,
∴,
∴.
∵,
∴,
∴,
∴,
即.
②如图3,延长交的延长线于点M,设,则.
由,
∴,
∴.
由,得,
,
解得.
由 得.
∵,
∴,
∴ .
∴,
∴,
∴.
∵,且,
∴,
∴.
设,则,得 ,
解得,
∴,
∴.
22.(1)证明:∵,
又∵,
∴,
∵,
∴,
∴;
(2)在上截取,由(1)知:,
又∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴;
(3)∵,
∴,
过点作于点,则:,
由(1)知:,
∴,
∴,
∴,
∵,
∴,
∴为等腰直角三角形,
∴,
∴,
∴,
∴在中,,
∴,
∴,
∴,
∴
.
23.(1)解:∵折叠,
∴,
∵,
∴,
∴,
∵,
∴,且,
∴,即;
(2)解:①由(1)可得,,
∴,
设,则,
∵,,
∴,,
∴,
∴,即,
整理得,,
解得,,
∴(负值舍去),
∴,
∴;
②由折叠的性质得,
∵,,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
∴
∵,
∴,
∴,
∵,
∴,
∴,
∴,
由①知,
∴,即,
∴,
∴,
∵
∴,
∴.
24.(1)证明:∵矩形,
∴,
,
,
平分.
(2)过作于.
在矩形中,,,
,,
,,
由(1)得平分,
,
,
,
又,
,
,
∵,,
∴,
,
,
;
(3),
矩形是正方形,
设,则,
由(2)知:,
,,
∴,
,平分,
∴,
,
,
,
.
25.(1)解:当限定自变量的取值范围为时,
则,
如果这条线段与函数的图象一点相交,
则反比例函数与直线的最右交点为,代入反比例函数可得,
反比例函数与直线的最左交点为,代入反比例函数可得,
(2)①解:∵,
∴抛物线的顶点,
将,代入得,
∴,
∴,,
如图,过点作垂足为,交轴于点,
则四边形为矩形,当时,与不平行
∴,
∵,,
∴,
∴,
∵,
∴,解得
∴抛物线的解析式为
如图,当时,过点作轴,垂足为,交轴于点,
则四边形为矩形,同理可得,
,
,
∴解得
∴抛物线的解析式为
综上所述,抛物线的解析式为或
②解:如图,当时,若线段与抛物线一点相交,则点与点重合或点在点下方,
∴,
∴或,
∵,
∴
如图,当,且点在点的下方时,若线段与抛物线一点相交,则点与点重合或点在点下方,
∴,
∴或,
∵,
∴,
如图,当,且点在点的上方时,则线段与抛物线一点相交,此时解得,
∵,
∴,
综上所述,当或或时,线段与抛物线一点相交.
26.解:(1),之间的数量关系是:.理由:
四边形为正方形,
,,
在和中,
,
,
,,
,
,
即.
,
.
在和中,
,
,
,
,
.
故答案为:;
(2)①(i)连接,如图,
四边形为正方形,
,,
,
由()知:.
正方形的边长为,,
.
设,则,.
,
,
.
,
;
(ii)过点作,交的延长线于点,如图,
四边形和四边形为正方形,
,,,
,,
,
在和中,
,
,
,,
,
,
,
为等腰直角三角形,
.
设,则,,.
.
Ⅰ.当时,,
.
,
.
此时,不合题意,舍去;
Ⅱ.当时,,
,
此时,点与点重合,
点与点重合,
;
Ⅲ.当时,.
则,
.
,
.
解得:
综上,若是等腰三角形,的长为或;
②过点作,交的延长线于点,延长,交于点,如图,
四边形和四边形为正方形,
,,,
,,
,
在和中,
,
,
,,
,
四边形为矩形,
,,
同理:四边形为矩形,
.
,
.
设,则,
.
,
.
,,
,
,
,
,
,
,
.
故答案为:.
27.(1)在与中,
,
∴;
(2)∵,
∴米.
在中,(米),
∴米,
∴滑梯的坡度为.
滑梯的坡度为;
(3)设点E向下滑动的距离为x米,则此时米
在中,,
当时,面积的最大,,
解得:,
∴面积最大值为平方米.
答案第1页,共2页
答案第1页,共2页
同课章节目录
