人教版八年级下册数学期中模拟试卷练习题(含答案)
文档属性
| 名称 | 人教版八年级下册数学期中模拟试卷练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 883.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 13:38:40 | ||
图片预览


文档简介
八年级下册数学人教版期中模拟试卷练习题
一、单选题
1.若则( )
A. B. C. D.
2.已知实数a,b,c在数轴上对应点的位置如图所示,化简( )
A. B.
C. D.
3.已知实数满足,那么的值是( )
A.2023 B.2024 C.2025 D.2026
4.在中,,,D为的中点,点在边上,且,连接.若的面积为6,则的长为( )
A.3 B. C. D.5
5.如图,有一架秋千,当它静止时,踏板离地的垂直高度,将它往前推送 (水平距离)时,踏板离地的垂直高度,秋千的绳索始终拉得很直,则秋千绳索的长度是( ).
A. B. C. D.
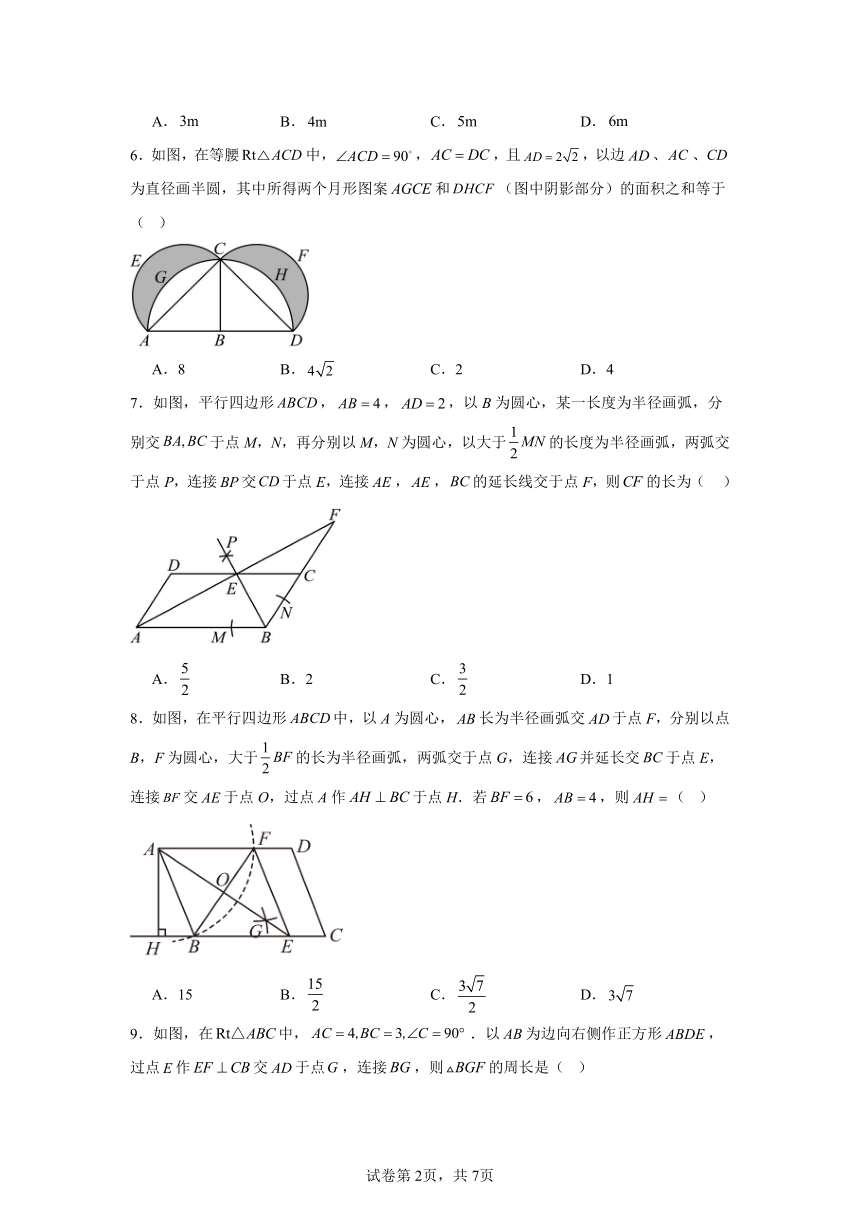
6.如图,在等腰中,,,且,以边、、为直径画半圆,其中所得两个月形图案和(图中阴影部分)的面积之和等于( )
A.8 B. C.2 D.4
7.如图,平行四边形,,,以B为圆心,某一长度为半径画弧,分别交于点M,N,再分别以M,N为圆心,以大于的长度为半径画弧,两弧交于点P,连接交于点E,连接,,的延长线交于点F,则的长为( )
A. B.2 C. D.1
8.如图,在平行四边形中,以A为圆心,长为半径画弧交于点F,分别以点B,F为圆心,大于的长为半径画弧,两弧交于点G,连接并延长交于点E,连接交于点O,过点A作于点H.若,,则( )
A.15 B. C. D.
9.如图,在中,.以为边向右侧作正方形,过点作交于点,连接,则的周长是( )
A.6 B.7 C.8 D.10
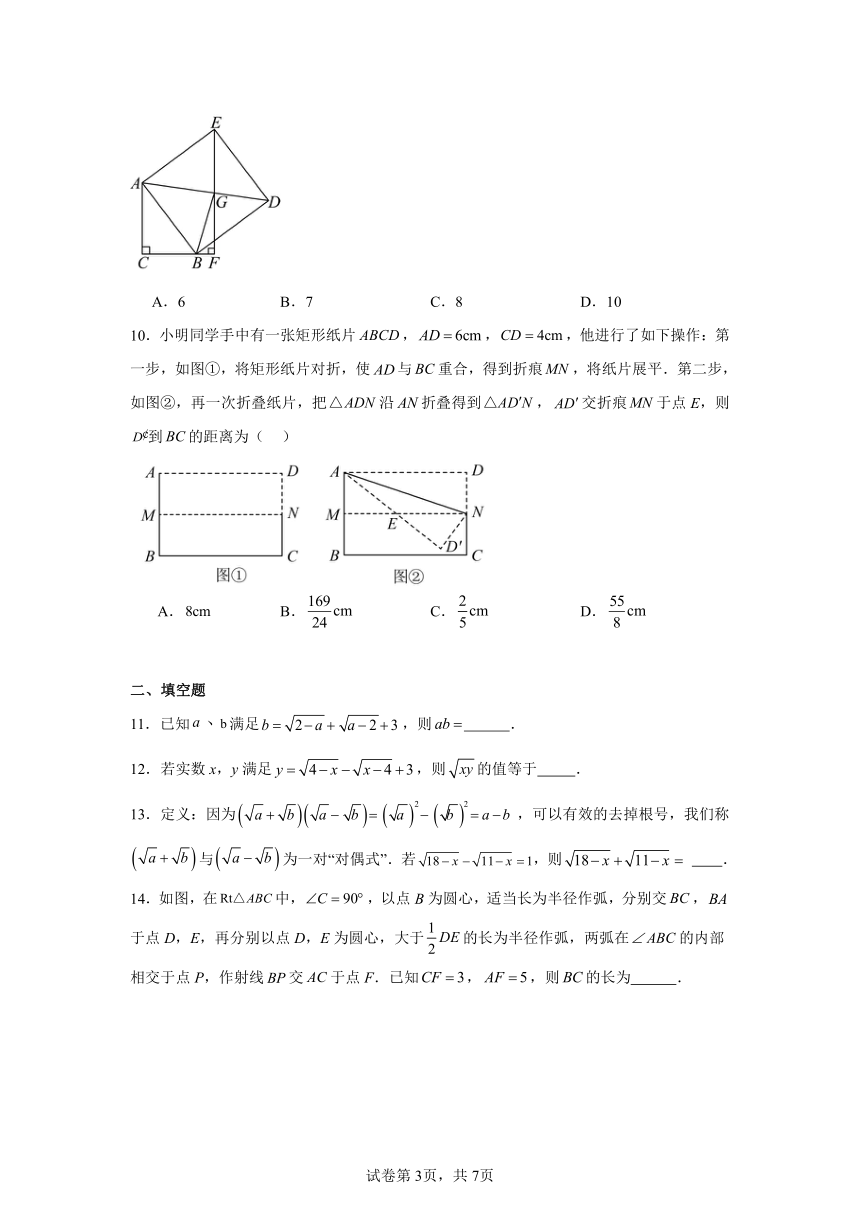
10.小明同学手中有一张矩形纸片,,,他进行了如下操作:第一步,如图①,将矩形纸片对折,使与重合,得到折痕,将纸片展平.第二步,如图②,再一次折叠纸片,把沿折叠得到,交折痕于点E,则到的距离为( )
A. B. C. D.
二、填空题
11.已知丶满足,则 .
12.若实数x,y满足,则的值等于 .
13.定义:因为,可以有效的去掉根号,我们称与为一对“对偶式”.若,则 .
14.如图,在中,,以点B为圆心,适当长为半径作弧,分别交,于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知,,则的长为 .
15.我们定义:有两边之比是的三角形叫“倍半三角形”.已知直角三角形是倍半三角形,如果,,那么的面积 .
16.如图,在中,,,M为斜边上一动点,过点作交于点,交于点,则线段的最小值为 .
17.如图,在四边形中,对角线,相交于点,其中,请你再添加一个条件,使四边形为平行四边形,可以添加的条件是 .
18.如图,在平行四边形中,,,,点E在上,连结,F为的中点,连结,,则长为 .
三、解答题
19.计算:
(1);
(2);
(3);
(4).
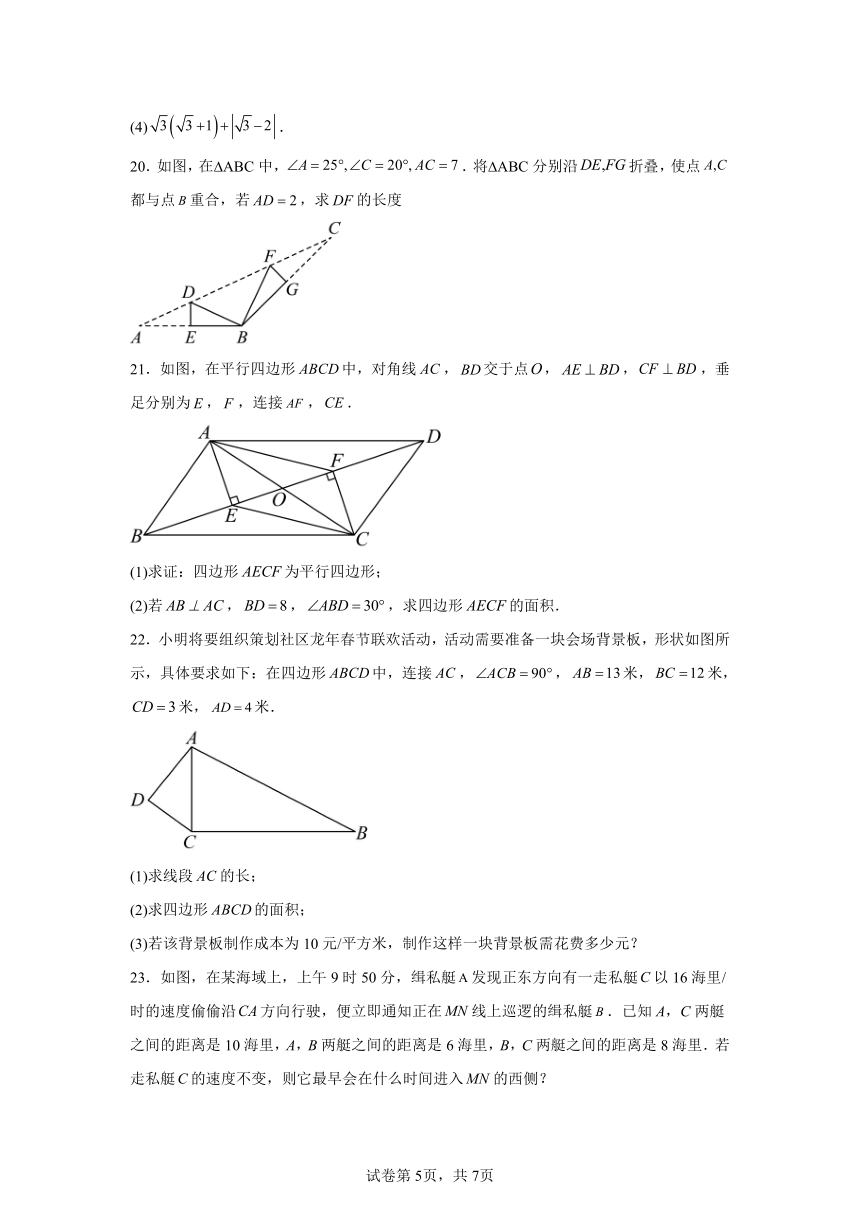
20.如图,在 ABC中,.将 ABC分别沿折叠,使点都与点重合,若,求的长度
21.如图,在平行四边形中,对角线,交于点,,,垂足分别为,,连接,.
(1)求证:四边形为平行四边形;
(2)若,,,求四边形的面积.
22.小明将要组织策划社区龙年春节联欢活动,活动需要准备一块会场背景板,形状如图所示,具体要求如下:在四边形中,连接,,米,米,米,米.
(1)求线段的长;
(2)求四边形的面积;
(3)若该背景板制作成本为10元/平方米,制作这样一块背景板需花费多少元?
23.如图,在某海域上,上午9时50分,缉私艇发现正东方向有一走私艇以16海里/时的速度偷偷沿方向行驶,便立即通知正在线上巡逻的缉私艇.已知A,C两艇之间的距离是10海里,A,B两艇之间的距离是6海里,B,C两艇之间的距离是8海里.若走私艇的速度不变,则它最早会在什么时间进入的西侧?
24.在进行二次根式化简时,我们有时会碰上如这样的式子,我们可以将其进一步化:.这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
(1)化简:.
(2)若a是的小数部分,求的值.
(3)矩形的面积为,一边长为,求它的周长.
25.在学行四边形的性质后,小红进行了拓展性探究.她发现在平行四边形中,连接一条对角线,分别过另外两个顶点作这条对角线的垂线,则这两个顶点和垂足构成的四边形是平行四边形.可以利用平行四边形的判定方法得到此结论.请根据她的思路完成以下作图与填空:
(1)用直尺和圆规,过点作对角线的垂线,垂足为点,连接、.(只保留作图痕迹)
(2)已知:如图,在平行四边形中,连接,于点,于点.求证:四边形是平行四边形.
证明:四边形为平行四边形,
且.
①______.
,
,同理可得,.
②______
.
③______.
又,
,同理可得,.
.
④______.
四边形是平行四边形.
进一步思考:如果四边形是矩形呢?我们发现,在矩形中,连接一条对角线,分别过另外两个顶点作这条对角线的垂线,那么这两个顶点和垂足构成的四边形是⑤______.
26.请阅读下列材料:
问题:已知 ,求代数式 的值.
小明的做法如下:
,
,
两边平方,得:
,
,
.
把 作为整体代入,得 ,即把已知条件适当变形,再整体代入解决问题.
仿照上述方法解决下列问题:
(1)已知 ,求代数式 的值;
(2)已知 ,求代数式 的值.
试卷第1页,共3页
试卷第1页,共3页
《八年级下册数学人教版期中模拟试卷练习题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D C C C B C C C
11.6
12.
13.7
14.
15.1或或
16.
17..(答案不唯一)
18.
19.(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
20.解:∵,
∴,
由折叠得,,,,,
∴,
设,则,
在中,,
∴,
解得,
∴.
21.(1)证明:四边形是平行四边形,
,,
,
,,
,,
在和中,
,
,
,
又,
四边形为平行四边形;
(2)解:四边形是平行四边形,,
,
,
,
,
,,
,
,
,
,
,
,
.
22.(1)解:,米,米,
(米,
即线段的长为5米;
(2)解:,米,米,米,
,
是直角三角形,且,
(平方米),
(3)解:(元,
答:制作这样一块背景板需花费360元.
23.解:如图,设与相交于点,则.
,,
.
是直角三角形,且.
,
.
在中,由勾股定理,得.
(时)(分).
9时50分分时14分.
答:走私艇最早会在10时14分进入的西侧.
24.(1)解:
;
(2)解:∵a是的小数部分,,
∴,
;
(3)解:∵矩形的面积为,一边长为,
∴其邻边长为,
∴该矩形的周长为.
25.(1)如图,点E即为所作;
(2)证明:四边形为平行四边形,
且
,
,同理可得,
,
,
,
又,
,同理可得,,
,
,
四边形是平行四边形.
已知:如图,在矩形中,连接,于点,于点.求证:四边形是平行四边形.
证明:四边形为矩形,
且
,
,同理可得,
,
,
,
又,
,同理可得,,
,
,
四边形是平行四边形.
∴在矩形中,连接一条对角线,分别过另外两个顶点作这条对角线的垂线,那么这两个顶点和垂足构成的四边形是平行四边形.
26.(1)解:,
,
两边平方得:,即,
,
;
(2)解:,
,
,
两边平方,得,即,
,即,
.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.若则( )
A. B. C. D.
2.已知实数a,b,c在数轴上对应点的位置如图所示,化简( )
A. B.
C. D.
3.已知实数满足,那么的值是( )
A.2023 B.2024 C.2025 D.2026
4.在中,,,D为的中点,点在边上,且,连接.若的面积为6,则的长为( )
A.3 B. C. D.5
5.如图,有一架秋千,当它静止时,踏板离地的垂直高度,将它往前推送 (水平距离)时,踏板离地的垂直高度,秋千的绳索始终拉得很直,则秋千绳索的长度是( ).
A. B. C. D.
6.如图,在等腰中,,,且,以边、、为直径画半圆,其中所得两个月形图案和(图中阴影部分)的面积之和等于( )
A.8 B. C.2 D.4
7.如图,平行四边形,,,以B为圆心,某一长度为半径画弧,分别交于点M,N,再分别以M,N为圆心,以大于的长度为半径画弧,两弧交于点P,连接交于点E,连接,,的延长线交于点F,则的长为( )
A. B.2 C. D.1
8.如图,在平行四边形中,以A为圆心,长为半径画弧交于点F,分别以点B,F为圆心,大于的长为半径画弧,两弧交于点G,连接并延长交于点E,连接交于点O,过点A作于点H.若,,则( )
A.15 B. C. D.
9.如图,在中,.以为边向右侧作正方形,过点作交于点,连接,则的周长是( )
A.6 B.7 C.8 D.10
10.小明同学手中有一张矩形纸片,,,他进行了如下操作:第一步,如图①,将矩形纸片对折,使与重合,得到折痕,将纸片展平.第二步,如图②,再一次折叠纸片,把沿折叠得到,交折痕于点E,则到的距离为( )
A. B. C. D.
二、填空题
11.已知丶满足,则 .
12.若实数x,y满足,则的值等于 .
13.定义:因为,可以有效的去掉根号,我们称与为一对“对偶式”.若,则 .
14.如图,在中,,以点B为圆心,适当长为半径作弧,分别交,于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知,,则的长为 .
15.我们定义:有两边之比是的三角形叫“倍半三角形”.已知直角三角形是倍半三角形,如果,,那么的面积 .
16.如图,在中,,,M为斜边上一动点,过点作交于点,交于点,则线段的最小值为 .
17.如图,在四边形中,对角线,相交于点,其中,请你再添加一个条件,使四边形为平行四边形,可以添加的条件是 .
18.如图,在平行四边形中,,,,点E在上,连结,F为的中点,连结,,则长为 .
三、解答题
19.计算:
(1);
(2);
(3);
(4).
20.如图,在 ABC中,.将 ABC分别沿折叠,使点都与点重合,若,求的长度
21.如图,在平行四边形中,对角线,交于点,,,垂足分别为,,连接,.
(1)求证:四边形为平行四边形;
(2)若,,,求四边形的面积.
22.小明将要组织策划社区龙年春节联欢活动,活动需要准备一块会场背景板,形状如图所示,具体要求如下:在四边形中,连接,,米,米,米,米.
(1)求线段的长;
(2)求四边形的面积;
(3)若该背景板制作成本为10元/平方米,制作这样一块背景板需花费多少元?
23.如图,在某海域上,上午9时50分,缉私艇发现正东方向有一走私艇以16海里/时的速度偷偷沿方向行驶,便立即通知正在线上巡逻的缉私艇.已知A,C两艇之间的距离是10海里,A,B两艇之间的距离是6海里,B,C两艇之间的距离是8海里.若走私艇的速度不变,则它最早会在什么时间进入的西侧?
24.在进行二次根式化简时,我们有时会碰上如这样的式子,我们可以将其进一步化:.这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
(1)化简:.
(2)若a是的小数部分,求的值.
(3)矩形的面积为,一边长为,求它的周长.
25.在学行四边形的性质后,小红进行了拓展性探究.她发现在平行四边形中,连接一条对角线,分别过另外两个顶点作这条对角线的垂线,则这两个顶点和垂足构成的四边形是平行四边形.可以利用平行四边形的判定方法得到此结论.请根据她的思路完成以下作图与填空:
(1)用直尺和圆规,过点作对角线的垂线,垂足为点,连接、.(只保留作图痕迹)
(2)已知:如图,在平行四边形中,连接,于点,于点.求证:四边形是平行四边形.
证明:四边形为平行四边形,
且.
①______.
,
,同理可得,.
②______
.
③______.
又,
,同理可得,.
.
④______.
四边形是平行四边形.
进一步思考:如果四边形是矩形呢?我们发现,在矩形中,连接一条对角线,分别过另外两个顶点作这条对角线的垂线,那么这两个顶点和垂足构成的四边形是⑤______.
26.请阅读下列材料:
问题:已知 ,求代数式 的值.
小明的做法如下:
,
,
两边平方,得:
,
,
.
把 作为整体代入,得 ,即把已知条件适当变形,再整体代入解决问题.
仿照上述方法解决下列问题:
(1)已知 ,求代数式 的值;
(2)已知 ,求代数式 的值.
试卷第1页,共3页
试卷第1页,共3页
《八年级下册数学人教版期中模拟试卷练习题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D C C C B C C C
11.6
12.
13.7
14.
15.1或或
16.
17..(答案不唯一)
18.
19.(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
20.解:∵,
∴,
由折叠得,,,,,
∴,
设,则,
在中,,
∴,
解得,
∴.
21.(1)证明:四边形是平行四边形,
,,
,
,,
,,
在和中,
,
,
,
又,
四边形为平行四边形;
(2)解:四边形是平行四边形,,
,
,
,
,
,,
,
,
,
,
,
,
.
22.(1)解:,米,米,
(米,
即线段的长为5米;
(2)解:,米,米,米,
,
是直角三角形,且,
(平方米),
(3)解:(元,
答:制作这样一块背景板需花费360元.
23.解:如图,设与相交于点,则.
,,
.
是直角三角形,且.
,
.
在中,由勾股定理,得.
(时)(分).
9时50分分时14分.
答:走私艇最早会在10时14分进入的西侧.
24.(1)解:
;
(2)解:∵a是的小数部分,,
∴,
;
(3)解:∵矩形的面积为,一边长为,
∴其邻边长为,
∴该矩形的周长为.
25.(1)如图,点E即为所作;
(2)证明:四边形为平行四边形,
且
,
,同理可得,
,
,
,
又,
,同理可得,,
,
,
四边形是平行四边形.
已知:如图,在矩形中,连接,于点,于点.求证:四边形是平行四边形.
证明:四边形为矩形,
且
,
,同理可得,
,
,
,
又,
,同理可得,,
,
,
四边形是平行四边形.
∴在矩形中,连接一条对角线,分别过另外两个顶点作这条对角线的垂线,那么这两个顶点和垂足构成的四边形是平行四边形.
26.(1)解:,
,
两边平方得:,即,
,
;
(2)解:,
,
,
两边平方,得,即,
,即,
.
答案第1页,共2页
答案第1页,共2页
同课章节目录
