4.3 二倍角的三角函数公式 教学课件(共30张PPT) 高中数学:高一下学期北师大版(2019)必修第二册
文档属性
| 名称 | 4.3 二倍角的三角函数公式 教学课件(共30张PPT) 高中数学:高一下学期北师大版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 43.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 20:11:29 | ||
图片预览











文档简介
(共30张PPT)
4.3二倍角的三角函数公式
北师大版(2019)必修第二册
第四章 三角恒等变换
学习目标
能用二倍角公式推导出半角公式;
02
理解二倍角公式与两角和公式之间的联系,能利用两角和公式探索二倍角公式及相关变形式,并能进行简单的应用;
01
能利用三角恒等变换对三角函数式化简、求值以及证明三角恒等式,并能进行一些简单的应用.
03
知识回顾
回顾两角和的三角函数公式
,记作
sin(αβ)=,记作
tan(αβ)= ,记作.
若将公式中的 β 换成 α,
会得到什么结果?
问题:若Sα+β、Cα+β、Tα+β公式中 β=α,这些公式可化成什么样子?
两角和的正弦公式:
将公式中的 β 换成 α 可得:
二倍角公式
同理可得二倍角的余弦和正切公式
化简即得二倍角正弦公式:
注意:二倍角正切公式中的α、2α 均不等于 +kπ,k∈Z.
问题1 倍角公式中的“倍角”仅是指 α 与 2α 吗?
问题2 倍角公式中 α 的取值范围是多少?
对于S2α和C2α,α∈R,但是在使用时,要保证分母且有意义,
二倍角是相对的,如 4α 是 2α 的二倍角,α 是 的二倍角等,“倍”是描述两个数量之间关系的,这里蕴含着换元思想
即α≠ +kπ 且α≠ +kπ 且α≠ +kπ(k∈Z).
思考:根据同角三角函数的基本关系式sin2α+cos2α=1,你能否只用sin α或cos α表示cos 2α?
如何通过恒等变形解决上述问题?
分步
第1步,将公式sin2α+cos2α=1变形为:sin2α=1-cos2α,
第2步,将其代入二倍角余弦公式可得
cos 2α=cos2α-sin2α=cos2α-(1-cos2α)=2cos2α-1,
即得:cos 2α=2cos2α-1
cos 2α=cos2α-sin2α=(1-sin2α)-sin2α=1-2sin2α.
还可以将公式sin2α+cos2α=1变形为:cos2α=1-sin2α,再将其代入二倍角余弦公式可得:
二倍角余弦公式
三种形式
cos 2α=-
cos 2α=2-1
cos 2α=1-2
问题:余弦的二倍角公式还有哪些变形?
由cos 2α=2cos2α-1 升幂变形得: 1+cos 2α=2cos2α
升幂公式:
1+cos 2α=2cos2α
1-cos 2α=2sin2α
观察一下二倍角余弦公式中项的次数,可以做怎样变形?
相应的,我们也可对其作降幂变形:
由cos 2α=1-2sin2α 升幂变形得:1-cos 2α=2sin2α
由cos 2α=2cos2α-1降幂变形得:
由cos 2α=1-2sin2α 降幂变形得:
降幂公式:
例1 已知角 α 是第二象限角,cosα= ,如何求 sin2α,cos2α 和 tan2α 的值?
解:因为角α是第二象限角且
,得
例2 在△ABC 中,已知 AB=AC=2BC,求角 A 的正弦值.
A
B
D
C
θ
解:如图,过点 A 作 BC 的垂线,垂足为 D.设∠BAD=θ,则∠BAC=2θ,
因为AB=AC=2BC,BC=2BD,
所以AB=4BD,AD=,
所以
故sin∠BAC=
例3 要把半径为 R 的半圆形木料截成矩形,应怎样截取,才能使矩形面积最大?
α
R
O
B
A
解:如图,设圆心为 O,矩形面积为 S,∠AOB=α,
则 AB=Rsin α,OB=Rcos α,
S=Rsin α·2(Rcos α)=2R2sin αcos α=R2sin 2α,
当sin 2α取得最大值1,即 时,矩形面积最大,最大面积等于R2.
思考:在利用二倍角公式解决问题时,已知角 α 的一个三角函数值和它所在的象限就可以求出这个角的二倍角的所有三角函数值.如果已知一个角 α 的一个三角函数值,能否求出这个角的半角 的所有三角函数值?
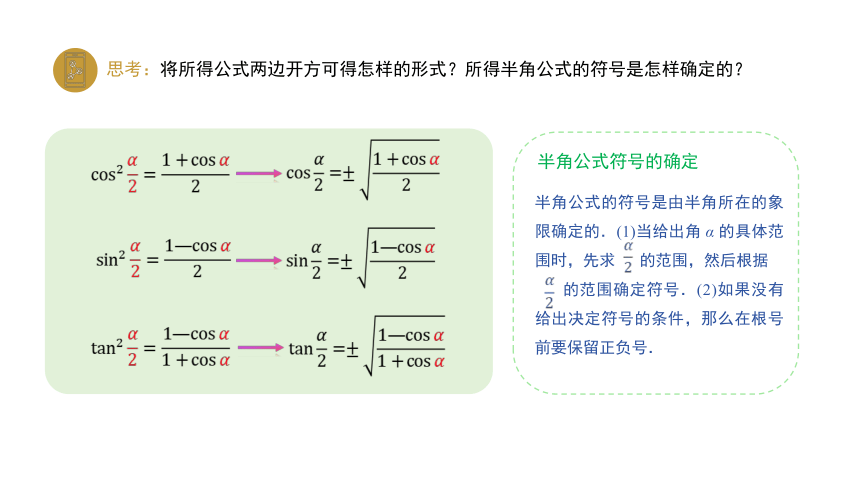
思考:将所得公式两边开方可得怎样的形式?所得半角公式的符号是怎样确定的?
半角公式的符号是由半角所在的象限确定的.(1)当给出角 α 的具体范围时,先求 的范围,然后根据
的范围确定符号.(2)如果没有给出决定符号的条件,那么在根号前要保留正负号.
半角公式符号的确定
问题:根据正切函数定义,还可以得到 的哪些变形?
变形二:
变形一:
例4 求 的值.
解析:因为
所以
例5 已知 ,求 .
解析:因为
又因为 ,故
所以
当堂检测
B
B
B
B
B
二倍角公式:
公式变形:
二倍角公式
注意:二倍角正切公式中的α、2α 均不等于 +kπ,k∈Z.
降幂公式: ; .
升幂公式:1+cos 2α=2cos2α ;1-cos 2α=2sin2α.
1.牢记3组公式:
2.辨清1个易错点:
在、、 的公式中,应注意符号
的选取.
3.二倍角公式与半角公式之间的关系:
感谢您的聆听与指导
General template of fresh teaching
授课人:一一
4.3二倍角的三角函数公式
北师大版(2019)必修第二册
第四章 三角恒等变换
学习目标
能用二倍角公式推导出半角公式;
02
理解二倍角公式与两角和公式之间的联系,能利用两角和公式探索二倍角公式及相关变形式,并能进行简单的应用;
01
能利用三角恒等变换对三角函数式化简、求值以及证明三角恒等式,并能进行一些简单的应用.
03
知识回顾
回顾两角和的三角函数公式
,记作
sin(αβ)=,记作
tan(αβ)= ,记作.
若将公式中的 β 换成 α,
会得到什么结果?
问题:若Sα+β、Cα+β、Tα+β公式中 β=α,这些公式可化成什么样子?
两角和的正弦公式:
将公式中的 β 换成 α 可得:
二倍角公式
同理可得二倍角的余弦和正切公式
化简即得二倍角正弦公式:
注意:二倍角正切公式中的α、2α 均不等于 +kπ,k∈Z.
问题1 倍角公式中的“倍角”仅是指 α 与 2α 吗?
问题2 倍角公式中 α 的取值范围是多少?
对于S2α和C2α,α∈R,但是在使用时,要保证分母且有意义,
二倍角是相对的,如 4α 是 2α 的二倍角,α 是 的二倍角等,“倍”是描述两个数量之间关系的,这里蕴含着换元思想
即α≠ +kπ 且α≠ +kπ 且α≠ +kπ(k∈Z).
思考:根据同角三角函数的基本关系式sin2α+cos2α=1,你能否只用sin α或cos α表示cos 2α?
如何通过恒等变形解决上述问题?
分步
第1步,将公式sin2α+cos2α=1变形为:sin2α=1-cos2α,
第2步,将其代入二倍角余弦公式可得
cos 2α=cos2α-sin2α=cos2α-(1-cos2α)=2cos2α-1,
即得:cos 2α=2cos2α-1
cos 2α=cos2α-sin2α=(1-sin2α)-sin2α=1-2sin2α.
还可以将公式sin2α+cos2α=1变形为:cos2α=1-sin2α,再将其代入二倍角余弦公式可得:
二倍角余弦公式
三种形式
cos 2α=-
cos 2α=2-1
cos 2α=1-2
问题:余弦的二倍角公式还有哪些变形?
由cos 2α=2cos2α-1 升幂变形得: 1+cos 2α=2cos2α
升幂公式:
1+cos 2α=2cos2α
1-cos 2α=2sin2α
观察一下二倍角余弦公式中项的次数,可以做怎样变形?
相应的,我们也可对其作降幂变形:
由cos 2α=1-2sin2α 升幂变形得:1-cos 2α=2sin2α
由cos 2α=2cos2α-1降幂变形得:
由cos 2α=1-2sin2α 降幂变形得:
降幂公式:
例1 已知角 α 是第二象限角,cosα= ,如何求 sin2α,cos2α 和 tan2α 的值?
解:因为角α是第二象限角且
,得
例2 在△ABC 中,已知 AB=AC=2BC,求角 A 的正弦值.
A
B
D
C
θ
解:如图,过点 A 作 BC 的垂线,垂足为 D.设∠BAD=θ,则∠BAC=2θ,
因为AB=AC=2BC,BC=2BD,
所以AB=4BD,AD=,
所以
故sin∠BAC=
例3 要把半径为 R 的半圆形木料截成矩形,应怎样截取,才能使矩形面积最大?
α
R
O
B
A
解:如图,设圆心为 O,矩形面积为 S,∠AOB=α,
则 AB=Rsin α,OB=Rcos α,
S=Rsin α·2(Rcos α)=2R2sin αcos α=R2sin 2α,
当sin 2α取得最大值1,即 时,矩形面积最大,最大面积等于R2.
思考:在利用二倍角公式解决问题时,已知角 α 的一个三角函数值和它所在的象限就可以求出这个角的二倍角的所有三角函数值.如果已知一个角 α 的一个三角函数值,能否求出这个角的半角 的所有三角函数值?
思考:将所得公式两边开方可得怎样的形式?所得半角公式的符号是怎样确定的?
半角公式的符号是由半角所在的象限确定的.(1)当给出角 α 的具体范围时,先求 的范围,然后根据
的范围确定符号.(2)如果没有给出决定符号的条件,那么在根号前要保留正负号.
半角公式符号的确定
问题:根据正切函数定义,还可以得到 的哪些变形?
变形二:
变形一:
例4 求 的值.
解析:因为
所以
例5 已知 ,求 .
解析:因为
又因为 ,故
所以
当堂检测
B
B
B
B
B
二倍角公式:
公式变形:
二倍角公式
注意:二倍角正切公式中的α、2α 均不等于 +kπ,k∈Z.
降幂公式: ; .
升幂公式:1+cos 2α=2cos2α ;1-cos 2α=2sin2α.
1.牢记3组公式:
2.辨清1个易错点:
在、、 的公式中,应注意符号
的选取.
3.二倍角公式与半角公式之间的关系:
感谢您的聆听与指导
General template of fresh teaching
授课人:一一
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
