人教版八年级数学下册 18.1.2 平行四边形的判定 课时练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册 18.1.2 平行四边形的判定 课时练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1014.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 11:22:48 | ||
图片预览




文档简介
八年级数学下册人教版第十八章第1.2节《平行四边形的判定》
_
一、单选题
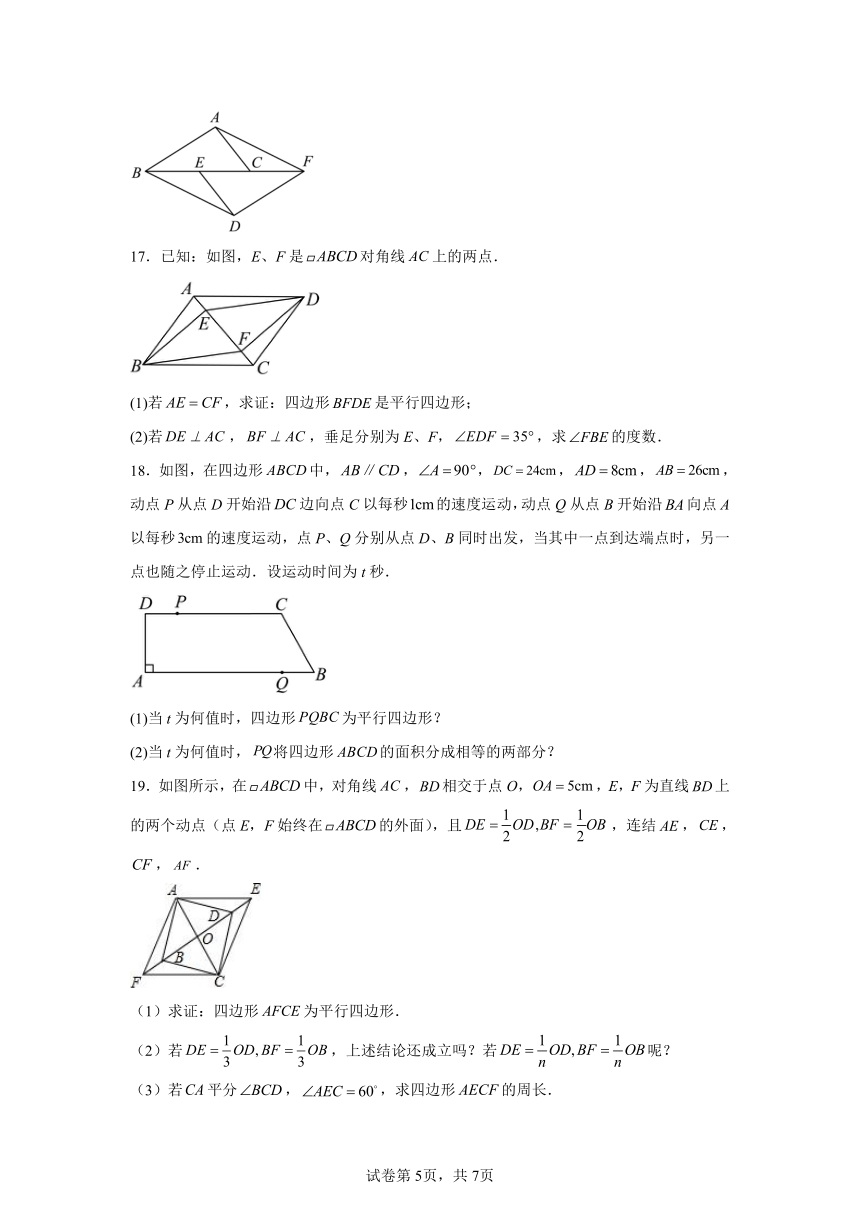
1.如图,在Rt ABC ABC中,,点为边的中点,连接,点E、F分别为、的中点,连接,若,则 ABC的面积为( )
A.12 B.15 C.60 D.30
2.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=5.正确的个数是( )
A.1个 B.2个
C.3个 D.4个
3.如图,已知四边形ABCD和四边形BCEF均为平行四边形,∠D=60°,连接AF,并延长交BE于点P,若AP⊥BE,AB=3,BC=2,AF=1,则BE的长为( )
A.5 B.2 C.2 D.3
4.如图,是的边延长线上一点,连接,,,交于点.添加以下条件,不能判定四边形为平行四边形的是( )
A. B.
C. D.
5.如图,在 ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线,若AE=3,BE=2,则平行四边形ABCD的面积为( )
A.3 B.6 C.8 D.12
6.下面有四个命题:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②一组对边相等,一组对角相等的四边形是平行四边形;
③一组对边相等,一条对角线平分另一条对角线的四边形是平行四边形;
④一组对角相等,连结这组对角的顶点的对角线平分另一条对角线的四边形是平行四边形.
其中,正确的命题是( )
A.④ B.③ C.②③ D.①④
7.如图,的对角线,相交于点,的平分线与边相交于点,是的中点,若,,则的长为( )
A. B. C. D.
二、填空题
8.在平面直角坐标系中,已知点,,请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是 .
9.如图,在四边形中,,对角线,交于点,现有三个条件①;②;③.其中可以判定四边形是平行四边形的有 (只写序号即可).
10.如图,在平行四边形中,,点P在边上以每秒的速度从点A向点D运动,点Q在边上以每秒的速度从点C出发,在间往返运动,两个点同时出发,当点P到达点D时停止运动,同时点Q 也停止运动.设运动时间为,开始运动以后,当以A,B,P,Q为顶点的四边形是平行四边形时,t的值为 .
11.如图,在 ABC中,,点是上的动点,连接,过点作,过点作交于点,当取得最小值时,则四边形的周长为 .
12.如图,四边形中,,,,是上一点,且,点从点出发以的速度向点运动,点从点出发,以的速度向点运动,当其中一点到达终点,另一点也随之停止,设运动时间为,则当以、、、为顶点的四边形是平行四边形时, .
13.如图,在平行四边形中,为上一点,,平分,,分别是,的中点,若,则的长为 .
14.如图,在平行四边形中,E,F分别是边上的动点,连接,点G、H分别为的中点,连接.若,则的最大值为 .
15.如图,在中,,点,分别从点,同时出发,沿,方向以相同的速度运动(分别运动到点,即停止),与相交于点,与相交于点.则在此运动过程中,线段的长始终等于 .
三、解答题
16.如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.
17.已知:如图,E、F是对角线上的两点.
(1)若,求证:四边形是平行四边形;
(2)若,,垂足分别为E、F,,求的度数.
18.如图,在四边形中,,,,,,动点P从点D开始沿边向点C以每秒的速度运动,动点Q从点B开始沿向点A以每秒的速度运动,点P、Q分别从点D、B同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒.
(1)当t为何值时,四边形为平行四边形?
(2)当t为何值时,将四边形的面积分成相等的两部分?
19.如图所示,在中,对角线,相交于点O,,E,F为直线上的两个动点(点E,F始终在的外面),且,连结,,,.
(1)求证:四边形为平行四边形.
(2)若,上述结论还成立吗?若呢?
(3)若平分,,求四边形的周长.
20.【方法运用】如图①,平行四边形的对角线和相交于点O,过点O且与、分别相交于点E、F,,的周长为10,求的值.
【拓展提升】如图②,平行四边形的对角线和相交于点O,过点O且与、的延长线分别相交于点E、F,连结点、,若,的面积为1,则四边形的面积为____________.
【拓展应用】如图③,若四边形是平行四边形,过点O作直线分别交边、于,过点O作直线分别交边、于G、H,且,若,,,则的长度是多少?
21.小红根据学习平行四边形的经验,对平行四边形进行了拓展探究.
【问题探究】
如图1,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)在网格中找一点D,画线段且使,连接;
(2)在括号内填写根据:
∵且CD=BA,
∴四边形是平行四边形(____________)
【拓展延伸】
(3)如图2,在四边形中,,厘米,厘米,点P、Q分别从点A、C同时出发,点P以2厘米/秒的速度由点A向点D运动,点Q以1厘米/秒的速度由点C向点B运动.当其中一点到达终点时,另一点也随之停止运动.请问:经过几秒,直线将四边形截出一个平行四边形?
22.[教材呈现]如图是人教版八年级下册数学教材P48页的部分内容:如图,,分别是的边,的中点,求证:,且.
[定理证明]乐乐给出如下部分证明:
证明:如图1,延长至点,使得,连接……
(1)请你根据乐乐添加的辅助线,写出完整的证明过程;(不再添加新的辅助线)
(2)[定理应用]如图2,在四边形中,,,,,点,,分别是,,的中点,求的长:
(3)如图3,在四边形中,点,,,分别是,,的中点,连接,,,.求证:四边形是平行四边形.
试卷第1页,共3页
试卷第1页,共3页
《八年级数学下册人教版第十八章第1.2节《平行四边形的判定》》参考答案
题号 1 2 3 4 5 6 7
答案 D C D D B A D
8.或或
9.①②/②①
10.3或9/9或3
11.
12.或.
13.
14.
15.
16.详解:证明:(1),
,
在 ABC和中,
,
≌;
(2)解:如图所示:
由(1)知 ABC≌,
,
,
,
四边形ABDF是平行四边形.
17.(1)证明:连接交于O,
∵,
∴,,
∵,
∴,即,
∴四边形是平行四边形.
(2)解:∵,,
∴,,
∵,
∴,,
∴,
在和中,
,
∴,
∴,
∴四边形是平行四边形
∴.
18.(1)解:由题意得,,则,,
∵,
∴当时,四边形是平行四边形,
则有,
解得,
当秒时,四边形是平行四边形;
(2)解:∵,,,,
∴梯形的面积为,
∵,,,
由题意得,
解得,
当为何值时,将四边形的面积分成相等的两部分.
19.解:(1)证明:四边形是平行四边形,
,.
,,
,
,
四边形为平行四边形.
(2),,
,
,
四边形为平行四边形.
上述结论成立,
由此可得出结论:若,,则四边形为平行四边形.
(3)在中,,
.
平分,
,
,
.
,
,
是的垂直平分线,
.
,
是等边三角形,
,
.
20.(1)【方法运用】解:∵四边形是平行四边形,,
∴,,
∴,
∵,
∴,
∴,,
∵的周长为10,
∴,
∴,
∴.
(2)【拓展提升】解:∵,的面积为1,
∴,
∵四边形是平行四边形,
∴,
∴;,
同【方法运用】得:,
∴,
∴,
∴,
故答案为:12;
(3)【拓展应用】解:∵,,
∴,
又∵ ,
∴而,
过作,,
∴,
∴,
∴,
由,,
∴,
故答案为:.
21.(1)解:如图所示;
(2)解:由平行四边形的判定定理可得判定四边形是平行四边形的依据是:一组对边平行且相等的四边形是平行四边形.
(3)解:经过x秒,直线将四边形截出一个平行四边形平行四边形,则:
米,米,米,米,
∵,
∴只需或或或,即得四边形是平行四边形.
①由,得:,解得: ;
②由,得:,解得:,不合题意,舍去;
③由,得:,解得:;
④由,得:,解得:.
答:经过1秒或秒或3秒,直线将四边形截出一个平行四边形.
22.(1)证明:如图1,延长至点,使得,连接,
∴,
∵点是的边的中点,
∴,
在和中,
,
∴,
∴,,
∴,
又∵点是的边的中点,
∴,
∴,
∴四边形是平行四边形,
∴,,
即,.
(2)解:∵如图2,点,,分别是,,的中点,,,,,
∴,,
,,
∴,,
∴,
∴,
∴在中,.
∴的长为.
(3)证明:如图3,连接,
∵点,,,分别是,,的中点,
∴,,
,,
∴,,
∴四边形是平行四边形.
答案第1页,共2页
答案第1页,共2页
_
一、单选题
1.如图,在Rt ABC ABC中,,点为边的中点,连接,点E、F分别为、的中点,连接,若,则 ABC的面积为( )
A.12 B.15 C.60 D.30
2.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=5.正确的个数是( )
A.1个 B.2个
C.3个 D.4个
3.如图,已知四边形ABCD和四边形BCEF均为平行四边形,∠D=60°,连接AF,并延长交BE于点P,若AP⊥BE,AB=3,BC=2,AF=1,则BE的长为( )
A.5 B.2 C.2 D.3
4.如图,是的边延长线上一点,连接,,,交于点.添加以下条件,不能判定四边形为平行四边形的是( )
A. B.
C. D.
5.如图,在 ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线,若AE=3,BE=2,则平行四边形ABCD的面积为( )
A.3 B.6 C.8 D.12
6.下面有四个命题:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②一组对边相等,一组对角相等的四边形是平行四边形;
③一组对边相等,一条对角线平分另一条对角线的四边形是平行四边形;
④一组对角相等,连结这组对角的顶点的对角线平分另一条对角线的四边形是平行四边形.
其中,正确的命题是( )
A.④ B.③ C.②③ D.①④
7.如图,的对角线,相交于点,的平分线与边相交于点,是的中点,若,,则的长为( )
A. B. C. D.
二、填空题
8.在平面直角坐标系中,已知点,,请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是 .
9.如图,在四边形中,,对角线,交于点,现有三个条件①;②;③.其中可以判定四边形是平行四边形的有 (只写序号即可).
10.如图,在平行四边形中,,点P在边上以每秒的速度从点A向点D运动,点Q在边上以每秒的速度从点C出发,在间往返运动,两个点同时出发,当点P到达点D时停止运动,同时点Q 也停止运动.设运动时间为,开始运动以后,当以A,B,P,Q为顶点的四边形是平行四边形时,t的值为 .
11.如图,在 ABC中,,点是上的动点,连接,过点作,过点作交于点,当取得最小值时,则四边形的周长为 .
12.如图,四边形中,,,,是上一点,且,点从点出发以的速度向点运动,点从点出发,以的速度向点运动,当其中一点到达终点,另一点也随之停止,设运动时间为,则当以、、、为顶点的四边形是平行四边形时, .
13.如图,在平行四边形中,为上一点,,平分,,分别是,的中点,若,则的长为 .
14.如图,在平行四边形中,E,F分别是边上的动点,连接,点G、H分别为的中点,连接.若,则的最大值为 .
15.如图,在中,,点,分别从点,同时出发,沿,方向以相同的速度运动(分别运动到点,即停止),与相交于点,与相交于点.则在此运动过程中,线段的长始终等于 .
三、解答题
16.如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.
17.已知:如图,E、F是对角线上的两点.
(1)若,求证:四边形是平行四边形;
(2)若,,垂足分别为E、F,,求的度数.
18.如图,在四边形中,,,,,,动点P从点D开始沿边向点C以每秒的速度运动,动点Q从点B开始沿向点A以每秒的速度运动,点P、Q分别从点D、B同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒.
(1)当t为何值时,四边形为平行四边形?
(2)当t为何值时,将四边形的面积分成相等的两部分?
19.如图所示,在中,对角线,相交于点O,,E,F为直线上的两个动点(点E,F始终在的外面),且,连结,,,.
(1)求证:四边形为平行四边形.
(2)若,上述结论还成立吗?若呢?
(3)若平分,,求四边形的周长.
20.【方法运用】如图①,平行四边形的对角线和相交于点O,过点O且与、分别相交于点E、F,,的周长为10,求的值.
【拓展提升】如图②,平行四边形的对角线和相交于点O,过点O且与、的延长线分别相交于点E、F,连结点、,若,的面积为1,则四边形的面积为____________.
【拓展应用】如图③,若四边形是平行四边形,过点O作直线分别交边、于,过点O作直线分别交边、于G、H,且,若,,,则的长度是多少?
21.小红根据学习平行四边形的经验,对平行四边形进行了拓展探究.
【问题探究】
如图1,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)在网格中找一点D,画线段且使,连接;
(2)在括号内填写根据:
∵且CD=BA,
∴四边形是平行四边形(____________)
【拓展延伸】
(3)如图2,在四边形中,,厘米,厘米,点P、Q分别从点A、C同时出发,点P以2厘米/秒的速度由点A向点D运动,点Q以1厘米/秒的速度由点C向点B运动.当其中一点到达终点时,另一点也随之停止运动.请问:经过几秒,直线将四边形截出一个平行四边形?
22.[教材呈现]如图是人教版八年级下册数学教材P48页的部分内容:如图,,分别是的边,的中点,求证:,且.
[定理证明]乐乐给出如下部分证明:
证明:如图1,延长至点,使得,连接……
(1)请你根据乐乐添加的辅助线,写出完整的证明过程;(不再添加新的辅助线)
(2)[定理应用]如图2,在四边形中,,,,,点,,分别是,,的中点,求的长:
(3)如图3,在四边形中,点,,,分别是,,的中点,连接,,,.求证:四边形是平行四边形.
试卷第1页,共3页
试卷第1页,共3页
《八年级数学下册人教版第十八章第1.2节《平行四边形的判定》》参考答案
题号 1 2 3 4 5 6 7
答案 D C D D B A D
8.或或
9.①②/②①
10.3或9/9或3
11.
12.或.
13.
14.
15.
16.详解:证明:(1),
,
在 ABC和中,
,
≌;
(2)解:如图所示:
由(1)知 ABC≌,
,
,
,
四边形ABDF是平行四边形.
17.(1)证明:连接交于O,
∵,
∴,,
∵,
∴,即,
∴四边形是平行四边形.
(2)解:∵,,
∴,,
∵,
∴,,
∴,
在和中,
,
∴,
∴,
∴四边形是平行四边形
∴.
18.(1)解:由题意得,,则,,
∵,
∴当时,四边形是平行四边形,
则有,
解得,
当秒时,四边形是平行四边形;
(2)解:∵,,,,
∴梯形的面积为,
∵,,,
由题意得,
解得,
当为何值时,将四边形的面积分成相等的两部分.
19.解:(1)证明:四边形是平行四边形,
,.
,,
,
,
四边形为平行四边形.
(2),,
,
,
四边形为平行四边形.
上述结论成立,
由此可得出结论:若,,则四边形为平行四边形.
(3)在中,,
.
平分,
,
,
.
,
,
是的垂直平分线,
.
,
是等边三角形,
,
.
20.(1)【方法运用】解:∵四边形是平行四边形,,
∴,,
∴,
∵,
∴,
∴,,
∵的周长为10,
∴,
∴,
∴.
(2)【拓展提升】解:∵,的面积为1,
∴,
∵四边形是平行四边形,
∴,
∴;,
同【方法运用】得:,
∴,
∴,
∴,
故答案为:12;
(3)【拓展应用】解:∵,,
∴,
又∵ ,
∴而,
过作,,
∴,
∴,
∴,
由,,
∴,
故答案为:.
21.(1)解:如图所示;
(2)解:由平行四边形的判定定理可得判定四边形是平行四边形的依据是:一组对边平行且相等的四边形是平行四边形.
(3)解:经过x秒,直线将四边形截出一个平行四边形平行四边形,则:
米,米,米,米,
∵,
∴只需或或或,即得四边形是平行四边形.
①由,得:,解得: ;
②由,得:,解得:,不合题意,舍去;
③由,得:,解得:;
④由,得:,解得:.
答:经过1秒或秒或3秒,直线将四边形截出一个平行四边形.
22.(1)证明:如图1,延长至点,使得,连接,
∴,
∵点是的边的中点,
∴,
在和中,
,
∴,
∴,,
∴,
又∵点是的边的中点,
∴,
∴,
∴四边形是平行四边形,
∴,,
即,.
(2)解:∵如图2,点,,分别是,,的中点,,,,,
∴,,
,,
∴,,
∴,
∴,
∴在中,.
∴的长为.
(3)证明:如图3,连接,
∵点,,,分别是,,的中点,
∴,,
,,
∴,,
∴四边形是平行四边形.
答案第1页,共2页
答案第1页,共2页
