2024-2025学年人教版八年级数学下册 18.2.3 正方形 课时练习(含答案)
文档属性
| 名称 | 2024-2025学年人教版八年级数学下册 18.2.3 正方形 课时练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览

文档简介
2024-2025学年八年级数学下册人教版第十八章第2.3节《正方形》课时练习
一、单选题
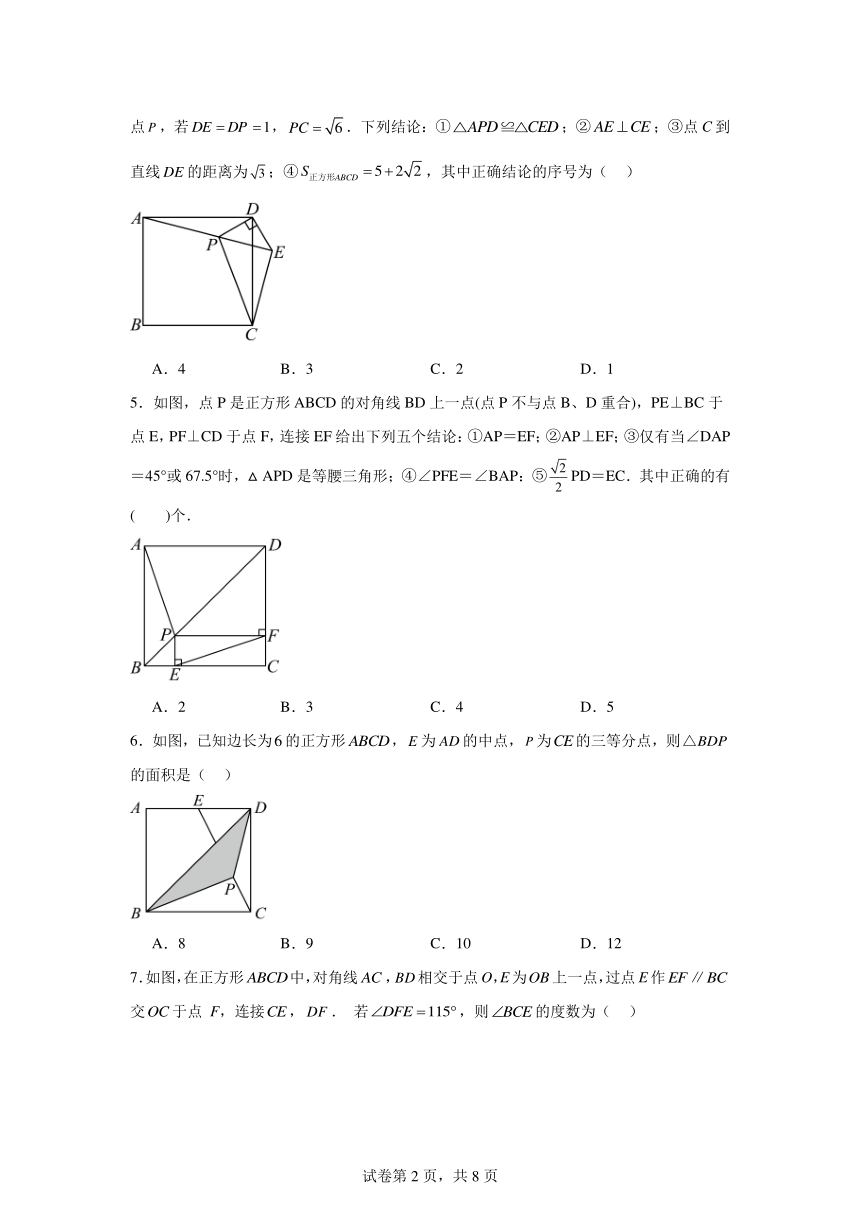
1.如图,正方形的边长为4,点在上且,为对角线上一动点,则周长的最小值为( ).
A.5 B.6 C.7 D.8
2.如图,在正方形中,对角线相交于点O.E、F分别为上一点,且,连接.若,则的度数为( )
A. B. C. D.
3.如图,正方形和正方形中,三点在同一直线上,点在上.,连接是的中点,连接,那么的长是( )
A. B. C. D.
4.如图,在正方形外取一点,连接,,,过点作的垂线交于点,若,.下列结论:①;②;③点C到直线的距离为;④,其中正确结论的序号为( )
A.4 B.3 C.2 D.1
5.如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤PD=EC.其中正确的有( )个.
A.2 B.3 C.4 D.5
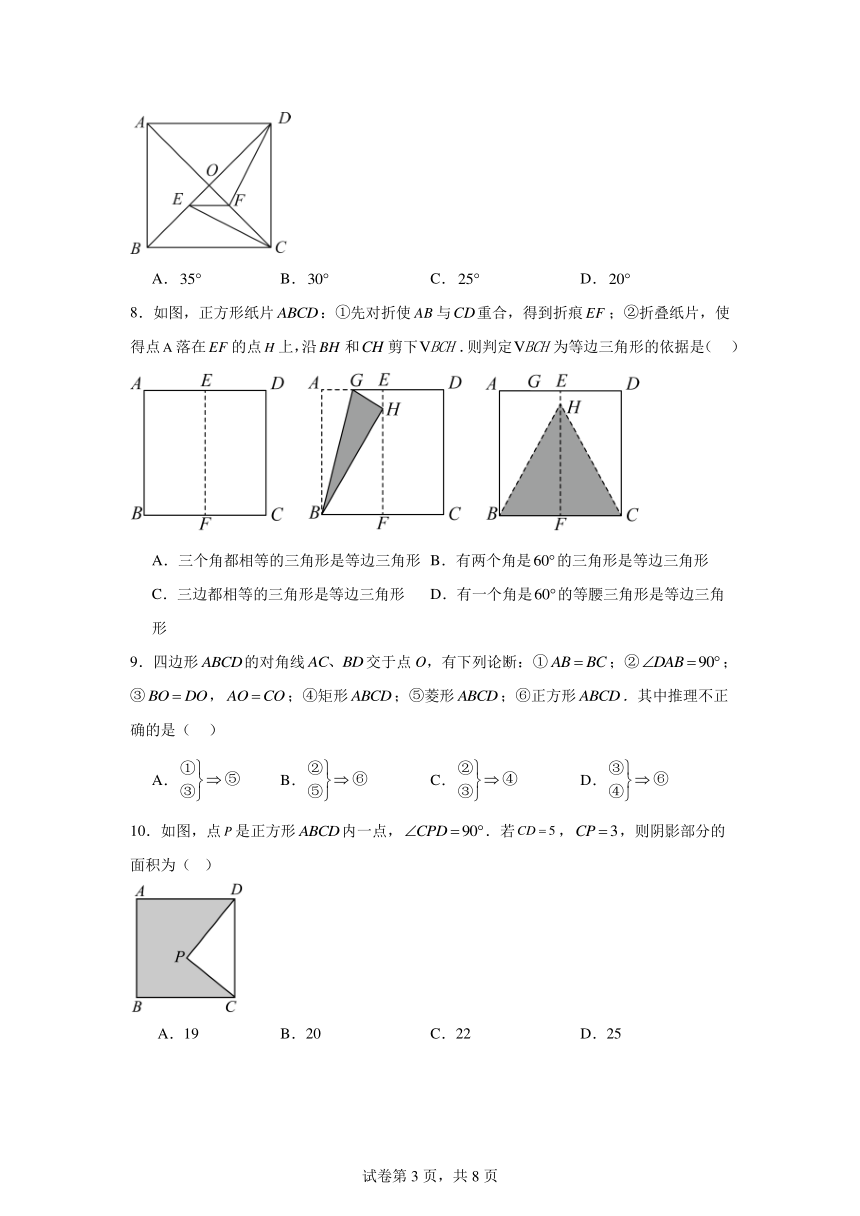
6.如图,已知边长为的正方形,为的中点,为的三等分点,则的面积是( )
A.8 B.9 C.10 D.12
7.如图,在正方形中,对角线,相交于点O,E为上一点,过点E作交于点 F,连接,. 若,则的度数为( )
A. B. C. D.
8.如图,正方形纸片:①先对折使与重合,得到折痕;②折叠纸片,使得点落在的点上,沿和剪下.则判定为等边三角形的依据是( )
A.三个角都相等的三角形是等边三角形 B.有两个角是的三角形是等边三角形
C.三边都相等的三角形是等边三角形 D.有一个角是的等腰三角形是等边三角形
9.四边形的对角线交于点O,有下列论断:①;②;③,;④矩形;⑤菱形;⑥正方形.其中推理不正确的是( )
A. B. C. D.
10.如图,点是正方形内一点,.若,,则阴影部分的面积为( )
A.19 B.20 C.22 D.25
二、填空题
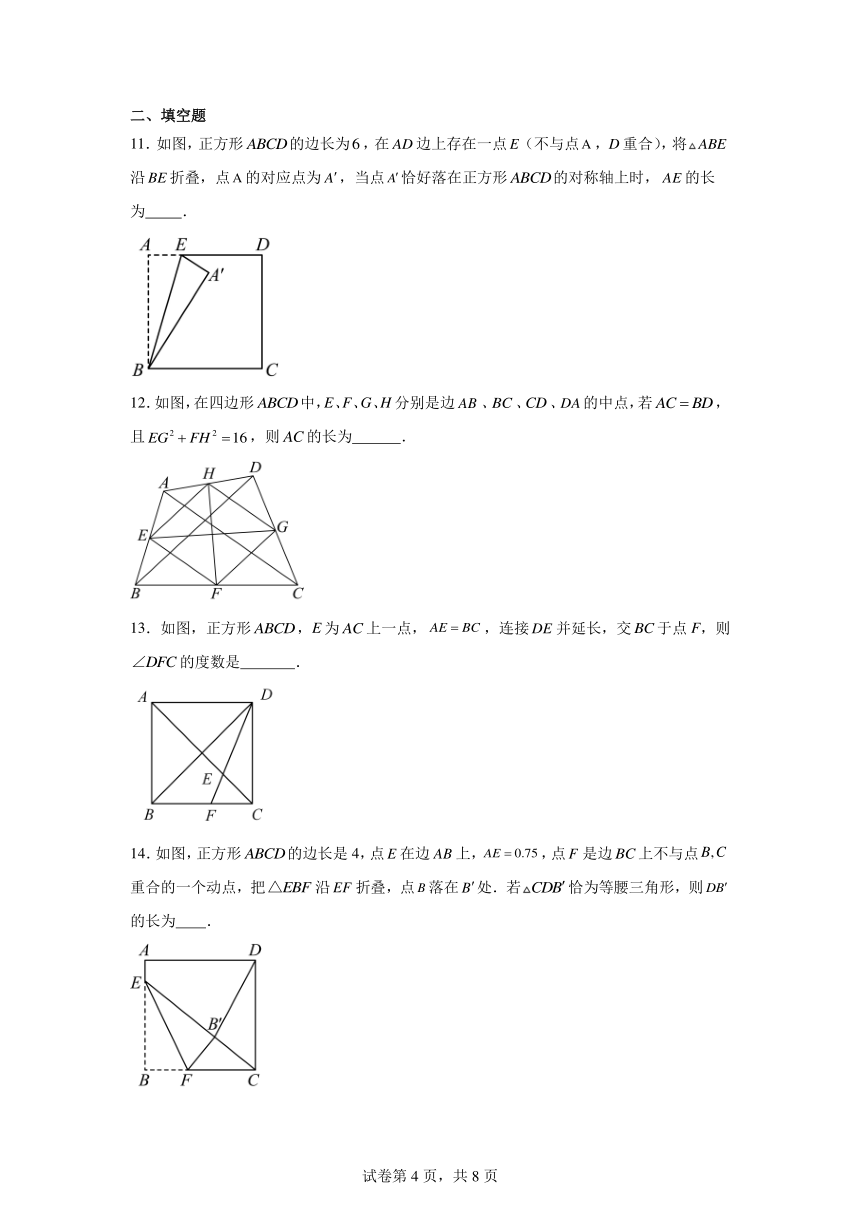
11.如图,正方形的边长为,在边上存在一点(不与点,重合),将沿折叠,点的对应点为,当点恰好落在正方形的对称轴上时,的长为 .
12.如图,在四边形中,E、F、G、H分别是边、、、的中点,若,且,则的长为 .
13.如图,正方形,E为上一点,,连接并延长,交于点F,则的度数是 .
14.如图,正方形的边长是4,点在边上,,点是边上不与点重合的一个动点,把沿折叠,点落在处.若恰为等腰三角形,则的长为 .
15.如图,正方形的边长为4;是边上一点,,连接,过点作于点,则的长为 .
16.七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,且边长为4,那么阴影部分面积为 .
17.如图,正方形中,点为射线上一个动点.连接,把沿折叠,当点的对应点刚好落在线段的垂直平分线上时, .
三、解答题
18.如图1,是我国古代著名的“赵爽弦图”,它是由4个全等的直角三角形围成,即
,其中四边形是正方形,四边形是正方形,如图2,将图1中的线段和线段分别延长到点和点,使,,连接,,,,得到四边形.
(1)求证:四边形是平行四边形;
(2)若,,求四边形的面积.
19.如图,在中,,,,点D从点C出发沿方向以的速度向点A匀速运动,同时点E从点A出发沿方向以的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作于点F,连接、.
备用图
(1)四边形能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(2)四边形能够成为正方形吗?如果能,求出相应的t值;如果不能,请说明理由.
20.如图,点D,E,F分别是,,的中点,连接,,,;
(1)求证:,相平分;
(2)现有三个条件:①;②平分;③;
请你从中选择两个条件(写序号): 使得四边形是正方形,并加以证明.
21.如图,点是正方形边上一动点(不与、重合),是外角的平分线,点在射线上.
(1)当时,判断与是否垂直,并证明结论;
(2)若在点运动过程中,线段与始终满足关系式.
①连接,证明的值为常量;
②设与的交点为,的周长为,求正方形的面积.
22.四边形为正方形,点为线段上一点,连接,过点作,交射线于点,以为邻边作矩形,连接.
(1)如图,求证:矩形是正方形;
(2)若,,求的长度;
(3)当线段与正方形的某条边的夹角是时,求的度数.
23.定义:对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”,如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”
【概念理解】
(1)在已经学过的“①平行四边形;②矩形;③菱形;④正方形”中,_________是“中方四边形”(填序号).
【性质探究】
(2)如图1,若四边形是“中方四边形”,观察图形,线段和线段有什么关系,并证明你的结论.
【问题解决】
(3)如图2,以锐角的两边为边长,分别向外侧作正方形和正方形连结,依次连接四边形的四边中点得到四边形.求证:四边形是“中方四边形”.
试卷第1页,共3页
试卷第1页,共3页
《2024-2025学年八年级数学下册人教版第十八章第2.3节《正方形》课时练习》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B A B D B C C D A
11.或或
12.4
13.
14.4或/或4
15.//
16.3
17.或/或
18.(1)(1)证明:,
,,,
,,
,
,,
,,
在和中,
,
,
;
在和中,
,
,
,
四边形是平行四边形.
(2)解:,,
,,
,,
,,
,,
四边形是正方形,
,
,
四边形的面积是86.
19.(1)四边形能够成为菱形,理由如下:
∵中,,,
.
在中,,,
,
,,
四边形是平行四边形,
当时,四边形是菱形,
即,解得:,
即当时,四边形是菱形;
(2)四边形不能为正方形,理由如下:
当时,.
,
,
,
,
时,
但,
四边形不可能为正方形.
20.(1)证明:、、分别是,,的中点,
、都是△ABC的中位线,
∴,,
四边形为平行四边形,
、互相平分;
(2)解:①;②平分;③,
∵四边形为平行四边形,
∴添加①时,四边形是矩形;
添加②平分时,,则,此时四边形是菱形;
添加③时,由得到,四边形是菱形;
∴选择①③或①②时,四边形是正方形;
选择①③,
证明:四边形为平行四边形,,
四边形是矩形,
点、分别是、的中点,
是△ABC的中位线,
∴,
,
,
四边形是正方形,
选择①②,
证明:四边形为平行四边形,,
四边形是矩形,
平分,
∴,
∵,
∴,
∴,
∴,此时四边形是菱形;
四边形是正方形,
故答案为:①③或①②.
21.(1)解:垂直.
证明:四边形是正方形,
,
,
,
,
,
.
(2)①如图:过点作,
,
四边形是矩形,
,,
,
平分,
,
为等腰直角三角形,
,
在中,根据勾股定理得:,
,
,
,
,
,
,
在和中
≌
,,
,
,
,
为等腰直角三角形,
在中,根据勾股定理得:,
,
,
的值为常量.
②如图:将绕点顺时针旋转,则点落在点处,点落在点处,得到,
,,,
为等腰直角三角形,
,
,
,
在和中
≌,
,
即:,
,
周长为:,
,
,
,
正方形面积为:.
22.(1)证明:如图,作于,于,
∵,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∴矩形是正方形;
(2)∵四边形是正方形,,
∴,, ,
∵,
∴,
∵四边形是正方形,
∴,,
∴,
∴,
∴;
(3)当与的夹角为时,如图,
∴,,
∴,
∵,
∴,
当与的夹角为时,如图,
过作于点,过作于点,
∵四边形是正方形,
∴,,
∴,
∴,
∴四边形为正方形,
∵四边形是矩形,
∴,,
∴,
又,
在和中,
,
∴,
∴,
综上所述:或 .
23.(1)解:在平行四边形、矩形、菱形、正方形中只有正方形是“中方四边形”,理由如下:
因为正方形的对角线相等且互相垂直,
故答案为:④;
(2)解:;
理由如下:如图1,
∵四边形是“中方四边形”,
∴是正方形且E、F、G、H分别是的中点,
∴,,,,
∴,
故答案为:,;
(3)证明:如图2,连接交于P,连接交于K,
∵四边形各边中点分别为M、N、R、L,
∴分别是的中位线,
∴,,,
∴,,
∴四边形是平行四边形,
∵四边形和四边形都是正方形,
∴,
∴,
即,
∴,
∴,
∴,
∴平行四边形是菱形,
∵,
∴.
又∵
∴,
∴,
又∵,
∴.
∴菱形是正方形,
即原四边形是“中方四边形”.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,正方形的边长为4,点在上且,为对角线上一动点,则周长的最小值为( ).
A.5 B.6 C.7 D.8
2.如图,在正方形中,对角线相交于点O.E、F分别为上一点,且,连接.若,则的度数为( )
A. B. C. D.
3.如图,正方形和正方形中,三点在同一直线上,点在上.,连接是的中点,连接,那么的长是( )
A. B. C. D.
4.如图,在正方形外取一点,连接,,,过点作的垂线交于点,若,.下列结论:①;②;③点C到直线的距离为;④,其中正确结论的序号为( )
A.4 B.3 C.2 D.1
5.如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤PD=EC.其中正确的有( )个.
A.2 B.3 C.4 D.5
6.如图,已知边长为的正方形,为的中点,为的三等分点,则的面积是( )
A.8 B.9 C.10 D.12
7.如图,在正方形中,对角线,相交于点O,E为上一点,过点E作交于点 F,连接,. 若,则的度数为( )
A. B. C. D.
8.如图,正方形纸片:①先对折使与重合,得到折痕;②折叠纸片,使得点落在的点上,沿和剪下.则判定为等边三角形的依据是( )
A.三个角都相等的三角形是等边三角形 B.有两个角是的三角形是等边三角形
C.三边都相等的三角形是等边三角形 D.有一个角是的等腰三角形是等边三角形
9.四边形的对角线交于点O,有下列论断:①;②;③,;④矩形;⑤菱形;⑥正方形.其中推理不正确的是( )
A. B. C. D.
10.如图,点是正方形内一点,.若,,则阴影部分的面积为( )
A.19 B.20 C.22 D.25
二、填空题
11.如图,正方形的边长为,在边上存在一点(不与点,重合),将沿折叠,点的对应点为,当点恰好落在正方形的对称轴上时,的长为 .
12.如图,在四边形中,E、F、G、H分别是边、、、的中点,若,且,则的长为 .
13.如图,正方形,E为上一点,,连接并延长,交于点F,则的度数是 .
14.如图,正方形的边长是4,点在边上,,点是边上不与点重合的一个动点,把沿折叠,点落在处.若恰为等腰三角形,则的长为 .
15.如图,正方形的边长为4;是边上一点,,连接,过点作于点,则的长为 .
16.七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,且边长为4,那么阴影部分面积为 .
17.如图,正方形中,点为射线上一个动点.连接,把沿折叠,当点的对应点刚好落在线段的垂直平分线上时, .
三、解答题
18.如图1,是我国古代著名的“赵爽弦图”,它是由4个全等的直角三角形围成,即
,其中四边形是正方形,四边形是正方形,如图2,将图1中的线段和线段分别延长到点和点,使,,连接,,,,得到四边形.
(1)求证:四边形是平行四边形;
(2)若,,求四边形的面积.
19.如图,在中,,,,点D从点C出发沿方向以的速度向点A匀速运动,同时点E从点A出发沿方向以的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作于点F,连接、.
备用图
(1)四边形能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(2)四边形能够成为正方形吗?如果能,求出相应的t值;如果不能,请说明理由.
20.如图,点D,E,F分别是,,的中点,连接,,,;
(1)求证:,相平分;
(2)现有三个条件:①;②平分;③;
请你从中选择两个条件(写序号): 使得四边形是正方形,并加以证明.
21.如图,点是正方形边上一动点(不与、重合),是外角的平分线,点在射线上.
(1)当时,判断与是否垂直,并证明结论;
(2)若在点运动过程中,线段与始终满足关系式.
①连接,证明的值为常量;
②设与的交点为,的周长为,求正方形的面积.
22.四边形为正方形,点为线段上一点,连接,过点作,交射线于点,以为邻边作矩形,连接.
(1)如图,求证:矩形是正方形;
(2)若,,求的长度;
(3)当线段与正方形的某条边的夹角是时,求的度数.
23.定义:对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”,如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”
【概念理解】
(1)在已经学过的“①平行四边形;②矩形;③菱形;④正方形”中,_________是“中方四边形”(填序号).
【性质探究】
(2)如图1,若四边形是“中方四边形”,观察图形,线段和线段有什么关系,并证明你的结论.
【问题解决】
(3)如图2,以锐角的两边为边长,分别向外侧作正方形和正方形连结,依次连接四边形的四边中点得到四边形.求证:四边形是“中方四边形”.
试卷第1页,共3页
试卷第1页,共3页
《2024-2025学年八年级数学下册人教版第十八章第2.3节《正方形》课时练习》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B A B D B C C D A
11.或或
12.4
13.
14.4或/或4
15.//
16.3
17.或/或
18.(1)(1)证明:,
,,,
,,
,
,,
,,
在和中,
,
,
;
在和中,
,
,
,
四边形是平行四边形.
(2)解:,,
,,
,,
,,
,,
四边形是正方形,
,
,
四边形的面积是86.
19.(1)四边形能够成为菱形,理由如下:
∵中,,,
.
在中,,,
,
,,
四边形是平行四边形,
当时,四边形是菱形,
即,解得:,
即当时,四边形是菱形;
(2)四边形不能为正方形,理由如下:
当时,.
,
,
,
,
时,
但,
四边形不可能为正方形.
20.(1)证明:、、分别是,,的中点,
、都是△ABC的中位线,
∴,,
四边形为平行四边形,
、互相平分;
(2)解:①;②平分;③,
∵四边形为平行四边形,
∴添加①时,四边形是矩形;
添加②平分时,,则,此时四边形是菱形;
添加③时,由得到,四边形是菱形;
∴选择①③或①②时,四边形是正方形;
选择①③,
证明:四边形为平行四边形,,
四边形是矩形,
点、分别是、的中点,
是△ABC的中位线,
∴,
,
,
四边形是正方形,
选择①②,
证明:四边形为平行四边形,,
四边形是矩形,
平分,
∴,
∵,
∴,
∴,
∴,此时四边形是菱形;
四边形是正方形,
故答案为:①③或①②.
21.(1)解:垂直.
证明:四边形是正方形,
,
,
,
,
,
.
(2)①如图:过点作,
,
四边形是矩形,
,,
,
平分,
,
为等腰直角三角形,
,
在中,根据勾股定理得:,
,
,
,
,
,
,
在和中
≌
,,
,
,
,
为等腰直角三角形,
在中,根据勾股定理得:,
,
,
的值为常量.
②如图:将绕点顺时针旋转,则点落在点处,点落在点处,得到,
,,,
为等腰直角三角形,
,
,
,
在和中
≌,
,
即:,
,
周长为:,
,
,
,
正方形面积为:.
22.(1)证明:如图,作于,于,
∵,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∴矩形是正方形;
(2)∵四边形是正方形,,
∴,, ,
∵,
∴,
∵四边形是正方形,
∴,,
∴,
∴,
∴;
(3)当与的夹角为时,如图,
∴,,
∴,
∵,
∴,
当与的夹角为时,如图,
过作于点,过作于点,
∵四边形是正方形,
∴,,
∴,
∴,
∴四边形为正方形,
∵四边形是矩形,
∴,,
∴,
又,
在和中,
,
∴,
∴,
综上所述:或 .
23.(1)解:在平行四边形、矩形、菱形、正方形中只有正方形是“中方四边形”,理由如下:
因为正方形的对角线相等且互相垂直,
故答案为:④;
(2)解:;
理由如下:如图1,
∵四边形是“中方四边形”,
∴是正方形且E、F、G、H分别是的中点,
∴,,,,
∴,
故答案为:,;
(3)证明:如图2,连接交于P,连接交于K,
∵四边形各边中点分别为M、N、R、L,
∴分别是的中位线,
∴,,,
∴,,
∴四边形是平行四边形,
∵四边形和四边形都是正方形,
∴,
∴,
即,
∴,
∴,
∴,
∴平行四边形是菱形,
∵,
∴.
又∵
∴,
∴,
又∵,
∴.
∴菱形是正方形,
即原四边形是“中方四边形”.
答案第1页,共2页
答案第1页,共2页
