2024-2025学年湘教版八年级(下)数学期末模拟试题3(含解析)
文档属性
| 名称 | 2024-2025学年湘教版八年级(下)数学期末模拟试题3(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年湘教版八年级(下)数学期末模拟试题3
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列图形既是轴对称又是中心对称图形的是( )
A. B. C. D.
2.已知点与点B关于x轴对称,则点B的坐标是( )
A. B. C. D.
3.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等 C.对角线互相平分 D.邻边相等
4.在体育中考测试中,女生跳绳1分钟达143个以上为优秀,某校200名女生跳绳个数在143个以上的频率为,则该校女生跳绳成绩达到优秀的人数是( )
A.60人 B.100人 C.120人 D.150人
5.对于一次函数,下列结论正确的是( )
A.它的图象与轴交于点 B.随的增大而增大
C.当时, D.它的图象经过第一、二、三象限
6.如图是长方体水槽轴截面示意图,其底部放有一个实心铜球(铜的密度大于水),现向水槽中匀速注水,下列四个图象中能大致反映水槽中水的深度与注水时间关系的是( )
A. B. C. D.
7.如图,在平行四边形中,是的角平分线,,则( )
A. B. C. D.
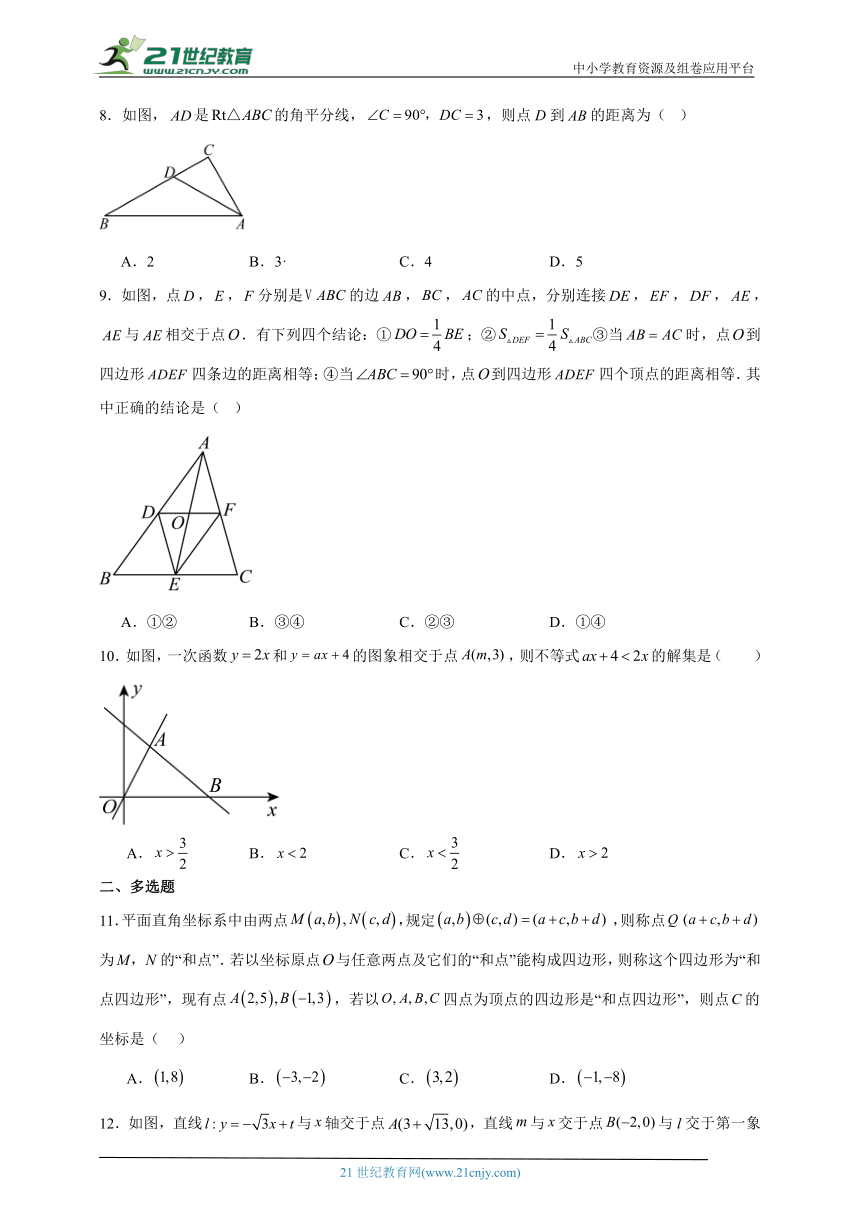
8.如图,是的角平分线,,则点D到的距离为( )
A.2 B.3· C.4 D.5
9.如图,点,,分别是的边,,的中点,分别连接,,,,与相交于点.有下列四个结论:①;②③当时,点到四边形四条边的距离相等;④当时,点到四边形四个顶点的距离相等.其中正确的结论是( )
A.①② B.③④ C.②③ D.①④
10.如图,一次函数和的图象相交于点,则不等式的解集是( )
A. B. C. D.
二、多选题
11.平面直角坐标系中由两点,规定,则称点为的“和点”.若以坐标原点与任意两点及它们的“和点”能构成四边形,则称这个四边形为“和点四边形”,现有点,若以四点为顶点的四边形是“和点四边形”,则点的坐标是( )
A. B. C. D.
12.如图,直线与轴交于点,直线与交于点与l交于第一象限内一点,点与点关于轴对称,点为直线上一动点,连接,若,,则的值为( )
A. B. C. D.
三、填空题
13.一个多边形的外角和等于它的内角和,则这个多边形的边数是 .
14.如图,数轴上点、所表示的数分别是,过点作数轴,个单位长度,以为圆心,长为半径画弧交数轴上点的左侧一点,则点表示的数是 .
15.为了解某校学生每周课外阅读时间的情况,随机抽取该校a名学生进行调查,获得的数据整理后绘制成统计表如下:
每周课外阅读时间/小时 合计
频数 8 17 b 15 a
频率 0.08 0.17 c 0.15 1
表中组的频数b满足.下面有四个推断:
①表中a的值为100;
②表中c的值可以为0.31:
③这a名学生每周课外阅读时间的中位数一定不在6~8之间:
④这名学生每周课外阅读时间的平均数不会超过6.
所有合理推断的序号是 .
16.如图,在平面直角坐标系中,正方形的顶点坐标为,则点的坐标为 .
17.若四条直线x=1,y=﹣1,y=3,y=kx﹣3所围成的凸四边形的面积等于12,则k的值为
18.如图,在正方形的边上有一点E,将直角三角形沿直线进行折叠,点F是点B的对应点,若,,则点F到边的距离是 .
四、解答题
19.已知函数.
(1)当m为何值时,y是x的一次函数?
(2)当m为何值时,y是x的正比例函数?
20.如图,将两个含角的三角尺摆放在一起,可以证得是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于,那么它所对的直角边等于斜边的一半.利用上述结论解答下列问题:
(1)在直角中,,若,则 ;
(2)在直角中,,若D是的中点,连接,求证:.
21.已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,,,,点E,F分别是BC,AD的中点.
(1)求证:;
(2)当与满足什么数量关系时,四边形是正方形?请证明.
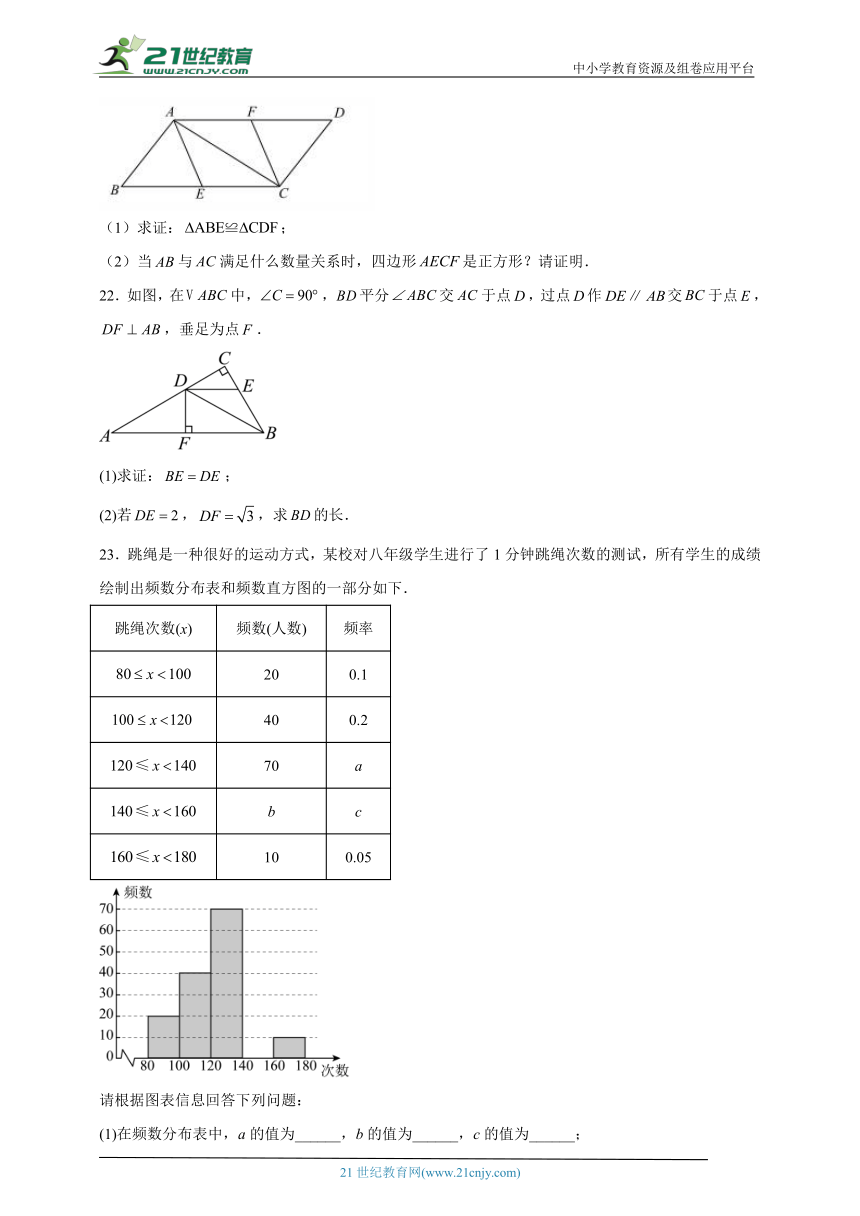
22.如图,在中,,平分交于点,过点作交于点,,垂足为点.
(1)求证:;
(2)若,,求的长.
23.跳绳是一种很好的运动方式,某校对八年级学生进行了1分钟跳绳次数的测试,所有学生的成绩绘制出频数分布表和频数直方图的一部分如下.
跳绳次数(x) 频数(人数) 频率
20 0.1
40 0.2
70 a
b c
10 0.05
请根据图表信息回答下列问题:
(1)在频数分布表中,a的值为______,b的值为______,c的值为______;
(2)将频数直方图补充完整;
(3)小健说“我的跳绳次数是此次测试所得数据的中位数”,小键的成绩在哪个范围内
(4)若跳绳次数在120次以上(含120次)属优良,求此次测试中成绩优良的人数占总人数的百分比.
24.近日,《我的阿勒泰》在网络上掀起了观剧热潮.该剧集以新疆阿勒泰为舞台,通过一系列温馨感人的故事,鲜活地展示了当地的风情民俗与居民的精神世界.某影视公司受此启发,计划制作两部不同题材但同样扎根现实的文艺作品,分别是关于乡村支教的《希望的田野》和展现传统手工艺传承的《指尖上的传承》.经了解,制作每集《希望的田野》比制作每集《指尖上的传承》的成本多100万元.该公司以8100万元制作《希望的田野》的集数与5400万元制作《指尖上的传承》集数相同.
(1)求制作《希望的田野》和《指尖上的传承》每集成本为多少万元.
(2)该影视公司计划拍摄《希望的田野》和《指尖上的传承》共60集,且《指尖上的传承》的集数不少于《希望的田野》集数的.完成后将两部文艺作品出售给某平台,该视频平台给出收购方案:《希望的田野》按每集450万元收购,《指尖上的传承》按每集320万元收购.若要使该影视公司收益最大化,应该如何制作这两部文艺作品?
25.在中,相交于点,分别过点作于点,于点,且.
(1)求证:四边形是平行四边形;
(2)若,求的长.
26.如图,在平面直角坐标系中,直线与轴,轴分别交于,两点,点为直线上一点,直线过点.
(1)求m和b的值;
(2)直线与轴交于点,动点在线段上从点开始以每秒1个单位的速度向点运动.设点的运动时间为秒.
①若的面积为10,求的值;
②是否存在的值,使为等腰三角形?若存在,直接写出的值;若不存在,请说明理由.
参考答案
1.【考点】轴对称图形的识别、中心对称图形的识别
【分析】本题考查了轴对称图形,中心对称图形的识别.解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形;在平面内,把一个图形绕着某个点旋转180度,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.根据中心对称和轴对称的定义,进行判断即可.
解:A、是轴对称图形,不是中心对称图形,故本选项不符合题意;
B、是中心对称图形,不是轴对称图形,故本选项不符合题意;
C、是轴对称图形,不是中心对称图形,故本选项不符合题意;
D、既是轴对称图形,又是中心对称图形,故本选项符合题意;
故选:D.
2.【考点】坐标与图形变化——轴对称
【分析】本题考查坐标与图形-轴对称变换,根据关于x轴对称的点的横坐标相同,纵坐标互为相反数求解即可.
解:∵点与点B关于x轴对称,
∴点B的坐标是,
故选:A.
3.【考点】利用菱形的性质证明、正方形性质理解
【分析】本题考查正方形和菱形的性质,根据对角线相等的菱形是正方形即可得出结果.
解:∵对角线相等的菱形是正方形,
∴正方形具有而菱形不一定具有的性质是对角线相等;
故选B.
4.【考点】根据数据描述求频数
【分析】本题考查求频数,熟练掌握相关知识是解题的关键,根据“频数总数频率”进行计算即可得到本题答案.
解:由题意得:(人),
故选:C.
5.【考点】判断一次函数的增减性、一次函数图象与坐标轴的交点问题、根据一次函数解析式判断其经过的象限
【分析】本题考查了一次函数的图象性质,根据一次函数,且,得出随的增大而减小,令,得出一次函数与轴交于点,它的图象经过第一、二、四象限,当时,则,即可作答.
解:∵一次函数,且,
∴随的增大而减小,故B选项不符合题意;
令时,则,即一次函数与轴交于点,
故A选项符合题意;
则一次函数经过第一、二、四象限,故D选项不符合题意;
∵一次函数的随的增大而减小,
∴令时,则,
∴当时,则,故C选项不符合题意;
故选:A.
6.【考点】用图象表示变量间的关系
【分析】本题主要考查函数的图象,根据题意可分两段进行分析:当水的深度未超过球顶时;当水的深度超过球顶时.分别分析出水槽中装水部分的宽度变化情况,进而判断出水的深度变化快慢,以此得出答案.
解:当水的深度未超过球顶时,
水槽中能装水的部分的宽度由下到上由宽逐渐变窄,再变宽,
所以在匀速注水过程中,水的深度变化先从上升较慢变为较快,再变为较慢;
当水的深度超过球顶时,
水槽中能装水的部分宽度不再变化,
所以在匀速注水过程中,水的深度的上升速度不会发生变化.
综上,水的深度先上升较慢,再变快,然后变慢,最后匀速上升.
故选:D.
7.【考点】角平分线的有关计算、两直线平行同旁内角互补、三角形内角和定理的应用、利用平行四边形的性质求解
【分析】由平行四边形的性质可得,,由两直线平行同旁内角互补可得,进而可得,由是的角平分线可得,由三角形的内角和定理可得,进而可得,解方程即可求出的度数.
解:四边形是平行四边形,
,,
,
是的角平分线,
,
,
,
解得:,
故选:.
【点评】本题主要考查了平行四边形的性质,三角形的内角和定理,两直线平行同旁内角互补,角平分线的有关计算等考点,熟练掌握平行四边形的性质及三角形的内角和定理是解题的关键.
8.【考点】角平分线的性质定理
【分析】本题主要考查角平分线的性质,掌握角平分线上的点到两边的距离相等成为解题的关键.
如图:过D点作垂足为E,然后根据角平分线的性质即可解答.
解:如图:过D点作垂足为E,
∵是的角平分线,,,
∴.
故选:B.
9.【考点】利用平行四边形性质和判定证明、与三角形中位线有关的证明、证明四边形是矩形、证明四边形是菱形
【分析】本题考查了平行四边形的判定与性质,菱形的判定与性质,矩形的判定与性质,三角形中位线定理.①根据三角形中位线定理即可解决问题;②根据三角形中位线定理和平行四边形的判定和性质定理,进而可以解决问题;③证明四边形是菱形,再根据菱形的性质即可解决问题;④证明四边形是平行四边形,进而可以解决问题.
解:①点,,分别是的边,,的中点,
,,,,
四边形是平行四边形,
,
是的中位线,
,故①错误;
②点,,分别是的边,,的中点,
,,,,,
四边形和四边形和四边形是平行四边形,
,
,故②正确;
③,
,
四边形是平行四边形,
四边形是菱形,
,是菱形两组对角的平分线,
点到四边形四条边的距离相等,故③正确;
④,四边形是平行四边形,
点到四边形四个顶点的距离不相等,故④错误.
综上所述:正确的是②③,
故选:C.
10.【考点】根据两条直线的交点求不等式的解集
【分析】此题主要考查了一次函数与一元一次不等式,关键是求出点坐标.
首先把代入,求出点坐标,再以交点为分界,结合图象写出不等式解集即可.
解:把点代入得,
,
解得:,
,
不等式的解集为.
故选:A.
11.【考点】坐标与图形、点坐标规律探索
【分析】以O,A,B,C四点为顶点的四边形是“和点四边形”,分3种情况讨论:①C为点A、B的“和点”;②B为A、C的“和点”;③A为B、C的“和点”,再根据点A、B的坐标求得点C的坐标.
∵以O,A,B,C四点为顶点的四边形是“和点四边形”,
①当C为A、B的“和点”时,C点的坐标为(2-1,5+3),即C(1,8);
②当B为A、C的“和点”时,设C点的坐标为(,),
则,解得C(-3,-2);
③当A为B、C的“和点”时,设C点的坐标为(,),
则,解得C(3,2);
∴点C的坐标为(1,8)或(-3,-2)或(3,2).
故选:ABC.
【点评】本题主要考查了点的坐标,解决问题的关键是掌握“和点”的定义和“和点四边形”的定义.
12.【考点】用勾股定理解三角形、等腰三角形的性质和判定、含30度角的直角三角形、一次函数与几何综合
【分析】先根据等角对等边得出.利用待定系数法求出直线的解析式,设直线与y轴交于点H,过点D作于点F,延长交y轴于点G,利用勾股定理、含30度角的直角三角形的性质求出点G的坐标,进而求出直线所在直线解析式,与直线的解析式联立,求出点F的坐标,利用勾股定理求出的长度,分E在F下方与上方两种情况,分别在E点下方、上方直线l上取一点M,使,利用勾股定理解即可.
解:,点与点关于轴对称,
,
,
,
.
将代入,得,
解得,
直线,
如图,设直线与y轴交于点H,过点D作于点F,延长交y轴于点G,
令,得,
,
又,
,
,,
,,
,
又,
,
,
,
设直线所在直线解析式为,
将,代入,得,
解得,
直线所在直线解析式为,
联立,
解得,
,
,
在中,,
解得.
分两种情况:
(1)当E在F下方时,如图,在E点下方直线l上取一点M,使,连接,
∵,
,
又∵,
,
又∵,
,
,
在中,,
;
(2)当E在F上方时,如图,在E点下方直线l上取一点M,使,连接,
同(1)可证,
,
在中,,
,
综上可知,的值为或.
故选.
【点评】本题考查求一次函数解析式,求两条直线的交点坐标,勾股定理,等腰三角形的判定与性质,三角形外角的定义和性质,含30度角的直角三角形的性质等,难度较大,正确作出辅助线,注意分情况讨论是解题的关键.
13.【考点】多边形内角和问题
【分析】本题考查了多边形的内角和外角,正确记忆多边形的外角和与边数无关,任何多边形的外角和都是是解题关键.根据多边形的内角和公式与外角和定理列出方程,然后求解即可.
解:设这个多边形是n边形,
根据题意得,
解得,
故答案为:4.
14.【考点】实数与数轴、勾股定理与无理数
【分析】本题考查了实数与数轴,勾股定理,熟练掌握相关考点是解题的关键.
根据题意求出,即可得到答案.
解:数轴,
数轴上点、所表示的数分别是,
,
,
,
,
点表示的数是,
故答案为: .
15.【考点】求中位数、频数分布表
【分析】①根据数据总数=频数÷频率,列式计算可求a的值;
②根据组的频数b满足,可求该范围的频数,进一步得到c的值的范围,从而求解;
③根据中位数的定义即可求解;
④根据加权平均数的计算公式即可求解.
解:①,故表中a的值为100,是合理推断;
②,,
,,
故表中c的值为,表中c的值可以为,是合理推断;
③表中组的频数b满足,
∴,,
∴这100名学生每周课外阅读时间的中位数可能在4~6之间,也可能在6~8之间,故此推断不是合理推断;
④这a名学生每周课外阅读时间的平均数可以超过6,故此推断不是合理推断.
综上,所有合理推断的序号是①②.
故答案为:①②.
【点评】本题考查频数(率)分布表,中位数,从表中获取数量及数量之间的关系是解决问题的关键.
16.【考点】根据正方形的性质求线段长、全等的性质和ASA(AAS)综合(ASA或者AAS)、写出直角坐标系中点的坐标
【分析】此题主要考查了正方形的性质,坐标与图形性质,全等三角形的判定与性质,过点作轴于,过点作轴于,于,则四边形为矩形,进而得到,,先证明,进而可证明和全等,则,,进而得到,,,由此可得点的坐标.
解:点作轴于,过点作轴于,于,如图,
则四边形为矩形,
,,,
,
四边形为正方形,
,,
点,
,,
,
,,
,,
,
,
,,
,
,,
点的坐标为,
故答案为:.
17.【考点】一次函数与几何综合
【分析】分别求出直线y=kx﹣3与直线y=﹣1,y=3的交点是A(,-1)、B(,3),直线x=1与直线y=﹣1,y=3的交点是C(1,3)、D(1,-1),根据梯形的面积公式可得关于k的方程即可求解.
直线y=kx﹣3与直线y=﹣1,y=3的交点是A(,-1)、B(,3),
直线x=1与直线y=﹣1,y=3的交点是C(1,3)、D(1,-1),
则四边形ABCD的面积是:
S=|AD+BC|×4=12,
所以,|AD+BC|=6,
|(-1)+(-1)|=6,
|-2|=6,
解得k=-2或1.
故答案为:-2或1.
【点评】考查了一次函数综合题,本题关键是得到凸四边形的四个交点坐标,涉及的考点有梯形的面积公式,以及方程思想的运用.
18.【考点】二次根式的乘法、用勾股定理解三角形、根据正方形的性质求线段长、折叠问题
【分析】如图,连接,过作于,证明,,,可得,,求解,,设,则,再利用勾股定理进一步解答即可.
解:如图,连接,过作于,
∵在正方形的边上有一点E,将直角三角形沿直线进行折叠,点F是点B的对应点, ,,
∴,,,设垂足为K,
∴,,
∴,
∴,
设,则,
∴,
解得:,
∴,
∴点F到边的距离是;
故答案为:
【点评】本题考查的是轴对称的性质,正方形的性质,勾股定理的应用,二次根式的运算,作出合适的辅助线是解本题的关键.
19.【考点】根据一次函数的定义求参数、正比例函数的定义
【分析】(1)利用一次函数定义进行解答即可;
(2)利用正比例函数定义进行解答.
(1)解:由题意得:,
解得:;
(2)解:由题意得:且,
解得:.
【点评】本题主要考查了正比例函数定义和一次函数定义,关键是掌握形如是常数,且的函数叫做正比例函数;形如是常数,且的函数叫做一次例函数.
20.【考点】含30度角的直角三角形、等边三角形的判定和性质
【分析】本题考查含30度角的直角三角形,等边三角形的判定和性质:
(1)直接利用结论进行求解即可;
(2)根据结论得到,进而推出为等边三角形,得到,即可得证.
(1)解:∵,,
∴;
故答案为:4.
(2)∵,
∴,
∵D是的中点,
∴,
∴为等边三角形,
∴,
∴.
21.【考点】证明四边形是正方形、证明四边形是菱形
【分析】(1)先证明得到,,由点E,F分别是BC,AD的中点得,,然后运用SSS证明即可;
(2)易证四边形是平行四边形,再证明四边形是平行四边形,证明AE=EC得平行四边形是菱形,由,点是的中点可证明菱形是正方形.
(1)证明:∵,,
∴
∵,
∴
∴,
∵点分别是,的中点
∴,,
∴
∴
(2)当时,四边形是正方形
理由:
∵,
∴四边形是平行四边形,
∴
∵点分别是,的中点
∴,,
∴
∴四边形是平行四边形.
∵,点是的中点
∴
∴平行四边形是菱形
∵,点是的中点
∴即
∴菱形是正方形.
【点评】此题主要考查了直角三角形斜边上的中线等于斜边的一半、菱形的判定以及正方形的判定等知识,熟练掌握判定定理以及性质定理是解答此题的关键.
22.【考点】用勾股定理解三角形、等腰三角形的性质和判定、角平分线的性质定理
【分析】本题考查了角平分线的性质,平行线的性质,勾股定理,等角对等边,掌握角平分线的性质是解题的关键.
()由角平分线的定义和平行线的性质可得,由等角对等边即可得出结论;
()由角平分线的性质可得,进而由勾股定理得,即可得,再利用勾股定理即可求解.
(1)证明:∵平分,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
又∵平分,,
∴,
∴在中,,
∵,
∴
∴在中,.
23.【考点】求中位数、频数分布直方图、频数分布表
【分析】本题考查频数分布表、频数分布直方图等知识,解题的关键是熟练掌握基本概念,属于基础题,中考常考题型.
(1)根据跳绳次数在的频数和频率求出抽取的人数,再用70除以总人数求出,再用整体1减去其它视力段的频率求出,进而求出b即可;
(2)根据(1)求出的数据直接补图即可;
(3)根据中位数的定义直接解答即可;
(4)跳绳次数在120次以上(含120次)所占的比例乘以即可.
(1)抽取的总人数是:(人,
则,
,
(人,
故答案为:,,;
(2)根据(1)求出的数据,补全频数分布直方图如下:
(3)中位数落在第3组内,
小健的成绩在的范围内;
(4)此次测试中成绩优良的人数占总人数的百分比为.
24.【考点】用一元一次不等式解决实际问题、最大利润问题(一次函数的实际应用)、分式方程的经济问题
【分析】本题考查了分式方程的应用、一次函数的应用、一元一次不等式的应用,理解题意,正确列出分式方程、一元一次不等式、一次函数解析式是解此题的关键.
(1)设制作《希望的田野》每集成本x万元,《指尖上的传承》每集成本万元,根据题意列出分式方程,解方程即可得解;
(2)设制作《希望的田野》m集,则制作《指尖上的传承》集,根据题意列出一元一次不等式,求出.设该影视公司收益为w万元,再求出关于的关系式,再由一次函数的性质计算即可得解.
(1)解:设制作《希望的田野》每集成本x万元,《指尖上的传承》每集成本万元.
根据题意,得,
解得,
经检验是方程的解,且符合题意.
.
答:制作《希望的田野》每集300万元,《指尖上的传承》每集200万元.
(2)解:设制作《希望的田野》m集,则制作《指尖上的传承》集,
根据题意,得,
解得.
设该影视公司收益为w万元,
则.
,
w随m的增大而增大.
又,
当时,w取最大值,此时.
答:制作《希望的田野》36集,《指尖上的传承》24集时,该影视公司收益最大.
25.【考点】用勾股定理解三角形、利用平行四边形性质和判定证明
【分析】本题考查了平行四边形的判定与性质,勾股定理,熟记各性质与判定是解题的关键.
(1)先证明,再根据对角线互相平分的四边形是平行四边形进行证明即可;
(2)根据勾股定理求出,再求出,在中,由勾股定理可求出的长.
(1)证明:四边形是平行四边形,
,
又,
,
,
又,
四边形是平行四边形;
(2)解:,
,
在中,由勾股定理得,,
,
,
四边形是平行四边形,
,
在中,由勾股定理得,,
.
26.【考点】等腰三角形的定义、一次函数图象与坐标轴的交点问题、求一次函数解析式
【分析】本题考查的是一次函数综合运用,涉及到等腰三角形的性质、面积的计算等,其中(3),要注意分类求解,避免遗漏.
(1)把点代入直线中得:,则点,直线过点,,;
(2)①由题意得:,,中,当时,,,,,即可求解;②分、、三种情况,分别求解即可.
(1)解:把点代入直线中得:,
点,
直线过点,
,;
(2)解:①由题意得:,
中,当时,,
,
,
中,当时,,
,
,
,
的面积为10,
,
,
则的值7秒;
②设点,点、的坐标为:、,
当时,则点在的中垂线上,即,
解得:;
当时,则点在点的正下方,故,
解得:;
当时,
同理可得:或(舍去)
故:当秒或秒或秒时,为等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024-2025学年湘教版八年级(下)数学期末模拟试题3
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列图形既是轴对称又是中心对称图形的是( )
A. B. C. D.
2.已知点与点B关于x轴对称,则点B的坐标是( )
A. B. C. D.
3.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等 C.对角线互相平分 D.邻边相等
4.在体育中考测试中,女生跳绳1分钟达143个以上为优秀,某校200名女生跳绳个数在143个以上的频率为,则该校女生跳绳成绩达到优秀的人数是( )
A.60人 B.100人 C.120人 D.150人
5.对于一次函数,下列结论正确的是( )
A.它的图象与轴交于点 B.随的增大而增大
C.当时, D.它的图象经过第一、二、三象限
6.如图是长方体水槽轴截面示意图,其底部放有一个实心铜球(铜的密度大于水),现向水槽中匀速注水,下列四个图象中能大致反映水槽中水的深度与注水时间关系的是( )
A. B. C. D.
7.如图,在平行四边形中,是的角平分线,,则( )
A. B. C. D.
8.如图,是的角平分线,,则点D到的距离为( )
A.2 B.3· C.4 D.5
9.如图,点,,分别是的边,,的中点,分别连接,,,,与相交于点.有下列四个结论:①;②③当时,点到四边形四条边的距离相等;④当时,点到四边形四个顶点的距离相等.其中正确的结论是( )
A.①② B.③④ C.②③ D.①④
10.如图,一次函数和的图象相交于点,则不等式的解集是( )
A. B. C. D.
二、多选题
11.平面直角坐标系中由两点,规定,则称点为的“和点”.若以坐标原点与任意两点及它们的“和点”能构成四边形,则称这个四边形为“和点四边形”,现有点,若以四点为顶点的四边形是“和点四边形”,则点的坐标是( )
A. B. C. D.
12.如图,直线与轴交于点,直线与交于点与l交于第一象限内一点,点与点关于轴对称,点为直线上一动点,连接,若,,则的值为( )
A. B. C. D.
三、填空题
13.一个多边形的外角和等于它的内角和,则这个多边形的边数是 .
14.如图,数轴上点、所表示的数分别是,过点作数轴,个单位长度,以为圆心,长为半径画弧交数轴上点的左侧一点,则点表示的数是 .
15.为了解某校学生每周课外阅读时间的情况,随机抽取该校a名学生进行调查,获得的数据整理后绘制成统计表如下:
每周课外阅读时间/小时 合计
频数 8 17 b 15 a
频率 0.08 0.17 c 0.15 1
表中组的频数b满足.下面有四个推断:
①表中a的值为100;
②表中c的值可以为0.31:
③这a名学生每周课外阅读时间的中位数一定不在6~8之间:
④这名学生每周课外阅读时间的平均数不会超过6.
所有合理推断的序号是 .
16.如图,在平面直角坐标系中,正方形的顶点坐标为,则点的坐标为 .
17.若四条直线x=1,y=﹣1,y=3,y=kx﹣3所围成的凸四边形的面积等于12,则k的值为
18.如图,在正方形的边上有一点E,将直角三角形沿直线进行折叠,点F是点B的对应点,若,,则点F到边的距离是 .
四、解答题
19.已知函数.
(1)当m为何值时,y是x的一次函数?
(2)当m为何值时,y是x的正比例函数?
20.如图,将两个含角的三角尺摆放在一起,可以证得是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于,那么它所对的直角边等于斜边的一半.利用上述结论解答下列问题:
(1)在直角中,,若,则 ;
(2)在直角中,,若D是的中点,连接,求证:.
21.已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,,,,点E,F分别是BC,AD的中点.
(1)求证:;
(2)当与满足什么数量关系时,四边形是正方形?请证明.
22.如图,在中,,平分交于点,过点作交于点,,垂足为点.
(1)求证:;
(2)若,,求的长.
23.跳绳是一种很好的运动方式,某校对八年级学生进行了1分钟跳绳次数的测试,所有学生的成绩绘制出频数分布表和频数直方图的一部分如下.
跳绳次数(x) 频数(人数) 频率
20 0.1
40 0.2
70 a
b c
10 0.05
请根据图表信息回答下列问题:
(1)在频数分布表中,a的值为______,b的值为______,c的值为______;
(2)将频数直方图补充完整;
(3)小健说“我的跳绳次数是此次测试所得数据的中位数”,小键的成绩在哪个范围内
(4)若跳绳次数在120次以上(含120次)属优良,求此次测试中成绩优良的人数占总人数的百分比.
24.近日,《我的阿勒泰》在网络上掀起了观剧热潮.该剧集以新疆阿勒泰为舞台,通过一系列温馨感人的故事,鲜活地展示了当地的风情民俗与居民的精神世界.某影视公司受此启发,计划制作两部不同题材但同样扎根现实的文艺作品,分别是关于乡村支教的《希望的田野》和展现传统手工艺传承的《指尖上的传承》.经了解,制作每集《希望的田野》比制作每集《指尖上的传承》的成本多100万元.该公司以8100万元制作《希望的田野》的集数与5400万元制作《指尖上的传承》集数相同.
(1)求制作《希望的田野》和《指尖上的传承》每集成本为多少万元.
(2)该影视公司计划拍摄《希望的田野》和《指尖上的传承》共60集,且《指尖上的传承》的集数不少于《希望的田野》集数的.完成后将两部文艺作品出售给某平台,该视频平台给出收购方案:《希望的田野》按每集450万元收购,《指尖上的传承》按每集320万元收购.若要使该影视公司收益最大化,应该如何制作这两部文艺作品?
25.在中,相交于点,分别过点作于点,于点,且.
(1)求证:四边形是平行四边形;
(2)若,求的长.
26.如图,在平面直角坐标系中,直线与轴,轴分别交于,两点,点为直线上一点,直线过点.
(1)求m和b的值;
(2)直线与轴交于点,动点在线段上从点开始以每秒1个单位的速度向点运动.设点的运动时间为秒.
①若的面积为10,求的值;
②是否存在的值,使为等腰三角形?若存在,直接写出的值;若不存在,请说明理由.
参考答案
1.【考点】轴对称图形的识别、中心对称图形的识别
【分析】本题考查了轴对称图形,中心对称图形的识别.解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形;在平面内,把一个图形绕着某个点旋转180度,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.根据中心对称和轴对称的定义,进行判断即可.
解:A、是轴对称图形,不是中心对称图形,故本选项不符合题意;
B、是中心对称图形,不是轴对称图形,故本选项不符合题意;
C、是轴对称图形,不是中心对称图形,故本选项不符合题意;
D、既是轴对称图形,又是中心对称图形,故本选项符合题意;
故选:D.
2.【考点】坐标与图形变化——轴对称
【分析】本题考查坐标与图形-轴对称变换,根据关于x轴对称的点的横坐标相同,纵坐标互为相反数求解即可.
解:∵点与点B关于x轴对称,
∴点B的坐标是,
故选:A.
3.【考点】利用菱形的性质证明、正方形性质理解
【分析】本题考查正方形和菱形的性质,根据对角线相等的菱形是正方形即可得出结果.
解:∵对角线相等的菱形是正方形,
∴正方形具有而菱形不一定具有的性质是对角线相等;
故选B.
4.【考点】根据数据描述求频数
【分析】本题考查求频数,熟练掌握相关知识是解题的关键,根据“频数总数频率”进行计算即可得到本题答案.
解:由题意得:(人),
故选:C.
5.【考点】判断一次函数的增减性、一次函数图象与坐标轴的交点问题、根据一次函数解析式判断其经过的象限
【分析】本题考查了一次函数的图象性质,根据一次函数,且,得出随的增大而减小,令,得出一次函数与轴交于点,它的图象经过第一、二、四象限,当时,则,即可作答.
解:∵一次函数,且,
∴随的增大而减小,故B选项不符合题意;
令时,则,即一次函数与轴交于点,
故A选项符合题意;
则一次函数经过第一、二、四象限,故D选项不符合题意;
∵一次函数的随的增大而减小,
∴令时,则,
∴当时,则,故C选项不符合题意;
故选:A.
6.【考点】用图象表示变量间的关系
【分析】本题主要考查函数的图象,根据题意可分两段进行分析:当水的深度未超过球顶时;当水的深度超过球顶时.分别分析出水槽中装水部分的宽度变化情况,进而判断出水的深度变化快慢,以此得出答案.
解:当水的深度未超过球顶时,
水槽中能装水的部分的宽度由下到上由宽逐渐变窄,再变宽,
所以在匀速注水过程中,水的深度变化先从上升较慢变为较快,再变为较慢;
当水的深度超过球顶时,
水槽中能装水的部分宽度不再变化,
所以在匀速注水过程中,水的深度的上升速度不会发生变化.
综上,水的深度先上升较慢,再变快,然后变慢,最后匀速上升.
故选:D.
7.【考点】角平分线的有关计算、两直线平行同旁内角互补、三角形内角和定理的应用、利用平行四边形的性质求解
【分析】由平行四边形的性质可得,,由两直线平行同旁内角互补可得,进而可得,由是的角平分线可得,由三角形的内角和定理可得,进而可得,解方程即可求出的度数.
解:四边形是平行四边形,
,,
,
是的角平分线,
,
,
,
解得:,
故选:.
【点评】本题主要考查了平行四边形的性质,三角形的内角和定理,两直线平行同旁内角互补,角平分线的有关计算等考点,熟练掌握平行四边形的性质及三角形的内角和定理是解题的关键.
8.【考点】角平分线的性质定理
【分析】本题主要考查角平分线的性质,掌握角平分线上的点到两边的距离相等成为解题的关键.
如图:过D点作垂足为E,然后根据角平分线的性质即可解答.
解:如图:过D点作垂足为E,
∵是的角平分线,,,
∴.
故选:B.
9.【考点】利用平行四边形性质和判定证明、与三角形中位线有关的证明、证明四边形是矩形、证明四边形是菱形
【分析】本题考查了平行四边形的判定与性质,菱形的判定与性质,矩形的判定与性质,三角形中位线定理.①根据三角形中位线定理即可解决问题;②根据三角形中位线定理和平行四边形的判定和性质定理,进而可以解决问题;③证明四边形是菱形,再根据菱形的性质即可解决问题;④证明四边形是平行四边形,进而可以解决问题.
解:①点,,分别是的边,,的中点,
,,,,
四边形是平行四边形,
,
是的中位线,
,故①错误;
②点,,分别是的边,,的中点,
,,,,,
四边形和四边形和四边形是平行四边形,
,
,故②正确;
③,
,
四边形是平行四边形,
四边形是菱形,
,是菱形两组对角的平分线,
点到四边形四条边的距离相等,故③正确;
④,四边形是平行四边形,
点到四边形四个顶点的距离不相等,故④错误.
综上所述:正确的是②③,
故选:C.
10.【考点】根据两条直线的交点求不等式的解集
【分析】此题主要考查了一次函数与一元一次不等式,关键是求出点坐标.
首先把代入,求出点坐标,再以交点为分界,结合图象写出不等式解集即可.
解:把点代入得,
,
解得:,
,
不等式的解集为.
故选:A.
11.【考点】坐标与图形、点坐标规律探索
【分析】以O,A,B,C四点为顶点的四边形是“和点四边形”,分3种情况讨论:①C为点A、B的“和点”;②B为A、C的“和点”;③A为B、C的“和点”,再根据点A、B的坐标求得点C的坐标.
∵以O,A,B,C四点为顶点的四边形是“和点四边形”,
①当C为A、B的“和点”时,C点的坐标为(2-1,5+3),即C(1,8);
②当B为A、C的“和点”时,设C点的坐标为(,),
则,解得C(-3,-2);
③当A为B、C的“和点”时,设C点的坐标为(,),
则,解得C(3,2);
∴点C的坐标为(1,8)或(-3,-2)或(3,2).
故选:ABC.
【点评】本题主要考查了点的坐标,解决问题的关键是掌握“和点”的定义和“和点四边形”的定义.
12.【考点】用勾股定理解三角形、等腰三角形的性质和判定、含30度角的直角三角形、一次函数与几何综合
【分析】先根据等角对等边得出.利用待定系数法求出直线的解析式,设直线与y轴交于点H,过点D作于点F,延长交y轴于点G,利用勾股定理、含30度角的直角三角形的性质求出点G的坐标,进而求出直线所在直线解析式,与直线的解析式联立,求出点F的坐标,利用勾股定理求出的长度,分E在F下方与上方两种情况,分别在E点下方、上方直线l上取一点M,使,利用勾股定理解即可.
解:,点与点关于轴对称,
,
,
,
.
将代入,得,
解得,
直线,
如图,设直线与y轴交于点H,过点D作于点F,延长交y轴于点G,
令,得,
,
又,
,
,,
,,
,
又,
,
,
,
设直线所在直线解析式为,
将,代入,得,
解得,
直线所在直线解析式为,
联立,
解得,
,
,
在中,,
解得.
分两种情况:
(1)当E在F下方时,如图,在E点下方直线l上取一点M,使,连接,
∵,
,
又∵,
,
又∵,
,
,
在中,,
;
(2)当E在F上方时,如图,在E点下方直线l上取一点M,使,连接,
同(1)可证,
,
在中,,
,
综上可知,的值为或.
故选.
【点评】本题考查求一次函数解析式,求两条直线的交点坐标,勾股定理,等腰三角形的判定与性质,三角形外角的定义和性质,含30度角的直角三角形的性质等,难度较大,正确作出辅助线,注意分情况讨论是解题的关键.
13.【考点】多边形内角和问题
【分析】本题考查了多边形的内角和外角,正确记忆多边形的外角和与边数无关,任何多边形的外角和都是是解题关键.根据多边形的内角和公式与外角和定理列出方程,然后求解即可.
解:设这个多边形是n边形,
根据题意得,
解得,
故答案为:4.
14.【考点】实数与数轴、勾股定理与无理数
【分析】本题考查了实数与数轴,勾股定理,熟练掌握相关考点是解题的关键.
根据题意求出,即可得到答案.
解:数轴,
数轴上点、所表示的数分别是,
,
,
,
,
点表示的数是,
故答案为: .
15.【考点】求中位数、频数分布表
【分析】①根据数据总数=频数÷频率,列式计算可求a的值;
②根据组的频数b满足,可求该范围的频数,进一步得到c的值的范围,从而求解;
③根据中位数的定义即可求解;
④根据加权平均数的计算公式即可求解.
解:①,故表中a的值为100,是合理推断;
②,,
,,
故表中c的值为,表中c的值可以为,是合理推断;
③表中组的频数b满足,
∴,,
∴这100名学生每周课外阅读时间的中位数可能在4~6之间,也可能在6~8之间,故此推断不是合理推断;
④这a名学生每周课外阅读时间的平均数可以超过6,故此推断不是合理推断.
综上,所有合理推断的序号是①②.
故答案为:①②.
【点评】本题考查频数(率)分布表,中位数,从表中获取数量及数量之间的关系是解决问题的关键.
16.【考点】根据正方形的性质求线段长、全等的性质和ASA(AAS)综合(ASA或者AAS)、写出直角坐标系中点的坐标
【分析】此题主要考查了正方形的性质,坐标与图形性质,全等三角形的判定与性质,过点作轴于,过点作轴于,于,则四边形为矩形,进而得到,,先证明,进而可证明和全等,则,,进而得到,,,由此可得点的坐标.
解:点作轴于,过点作轴于,于,如图,
则四边形为矩形,
,,,
,
四边形为正方形,
,,
点,
,,
,
,,
,,
,
,
,,
,
,,
点的坐标为,
故答案为:.
17.【考点】一次函数与几何综合
【分析】分别求出直线y=kx﹣3与直线y=﹣1,y=3的交点是A(,-1)、B(,3),直线x=1与直线y=﹣1,y=3的交点是C(1,3)、D(1,-1),根据梯形的面积公式可得关于k的方程即可求解.
直线y=kx﹣3与直线y=﹣1,y=3的交点是A(,-1)、B(,3),
直线x=1与直线y=﹣1,y=3的交点是C(1,3)、D(1,-1),
则四边形ABCD的面积是:
S=|AD+BC|×4=12,
所以,|AD+BC|=6,
|(-1)+(-1)|=6,
|-2|=6,
解得k=-2或1.
故答案为:-2或1.
【点评】考查了一次函数综合题,本题关键是得到凸四边形的四个交点坐标,涉及的考点有梯形的面积公式,以及方程思想的运用.
18.【考点】二次根式的乘法、用勾股定理解三角形、根据正方形的性质求线段长、折叠问题
【分析】如图,连接,过作于,证明,,,可得,,求解,,设,则,再利用勾股定理进一步解答即可.
解:如图,连接,过作于,
∵在正方形的边上有一点E,将直角三角形沿直线进行折叠,点F是点B的对应点, ,,
∴,,,设垂足为K,
∴,,
∴,
∴,
设,则,
∴,
解得:,
∴,
∴点F到边的距离是;
故答案为:
【点评】本题考查的是轴对称的性质,正方形的性质,勾股定理的应用,二次根式的运算,作出合适的辅助线是解本题的关键.
19.【考点】根据一次函数的定义求参数、正比例函数的定义
【分析】(1)利用一次函数定义进行解答即可;
(2)利用正比例函数定义进行解答.
(1)解:由题意得:,
解得:;
(2)解:由题意得:且,
解得:.
【点评】本题主要考查了正比例函数定义和一次函数定义,关键是掌握形如是常数,且的函数叫做正比例函数;形如是常数,且的函数叫做一次例函数.
20.【考点】含30度角的直角三角形、等边三角形的判定和性质
【分析】本题考查含30度角的直角三角形,等边三角形的判定和性质:
(1)直接利用结论进行求解即可;
(2)根据结论得到,进而推出为等边三角形,得到,即可得证.
(1)解:∵,,
∴;
故答案为:4.
(2)∵,
∴,
∵D是的中点,
∴,
∴为等边三角形,
∴,
∴.
21.【考点】证明四边形是正方形、证明四边形是菱形
【分析】(1)先证明得到,,由点E,F分别是BC,AD的中点得,,然后运用SSS证明即可;
(2)易证四边形是平行四边形,再证明四边形是平行四边形,证明AE=EC得平行四边形是菱形,由,点是的中点可证明菱形是正方形.
(1)证明:∵,,
∴
∵,
∴
∴,
∵点分别是,的中点
∴,,
∴
∴
(2)当时,四边形是正方形
理由:
∵,
∴四边形是平行四边形,
∴
∵点分别是,的中点
∴,,
∴
∴四边形是平行四边形.
∵,点是的中点
∴
∴平行四边形是菱形
∵,点是的中点
∴即
∴菱形是正方形.
【点评】此题主要考查了直角三角形斜边上的中线等于斜边的一半、菱形的判定以及正方形的判定等知识,熟练掌握判定定理以及性质定理是解答此题的关键.
22.【考点】用勾股定理解三角形、等腰三角形的性质和判定、角平分线的性质定理
【分析】本题考查了角平分线的性质,平行线的性质,勾股定理,等角对等边,掌握角平分线的性质是解题的关键.
()由角平分线的定义和平行线的性质可得,由等角对等边即可得出结论;
()由角平分线的性质可得,进而由勾股定理得,即可得,再利用勾股定理即可求解.
(1)证明:∵平分,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
又∵平分,,
∴,
∴在中,,
∵,
∴
∴在中,.
23.【考点】求中位数、频数分布直方图、频数分布表
【分析】本题考查频数分布表、频数分布直方图等知识,解题的关键是熟练掌握基本概念,属于基础题,中考常考题型.
(1)根据跳绳次数在的频数和频率求出抽取的人数,再用70除以总人数求出,再用整体1减去其它视力段的频率求出,进而求出b即可;
(2)根据(1)求出的数据直接补图即可;
(3)根据中位数的定义直接解答即可;
(4)跳绳次数在120次以上(含120次)所占的比例乘以即可.
(1)抽取的总人数是:(人,
则,
,
(人,
故答案为:,,;
(2)根据(1)求出的数据,补全频数分布直方图如下:
(3)中位数落在第3组内,
小健的成绩在的范围内;
(4)此次测试中成绩优良的人数占总人数的百分比为.
24.【考点】用一元一次不等式解决实际问题、最大利润问题(一次函数的实际应用)、分式方程的经济问题
【分析】本题考查了分式方程的应用、一次函数的应用、一元一次不等式的应用,理解题意,正确列出分式方程、一元一次不等式、一次函数解析式是解此题的关键.
(1)设制作《希望的田野》每集成本x万元,《指尖上的传承》每集成本万元,根据题意列出分式方程,解方程即可得解;
(2)设制作《希望的田野》m集,则制作《指尖上的传承》集,根据题意列出一元一次不等式,求出.设该影视公司收益为w万元,再求出关于的关系式,再由一次函数的性质计算即可得解.
(1)解:设制作《希望的田野》每集成本x万元,《指尖上的传承》每集成本万元.
根据题意,得,
解得,
经检验是方程的解,且符合题意.
.
答:制作《希望的田野》每集300万元,《指尖上的传承》每集200万元.
(2)解:设制作《希望的田野》m集,则制作《指尖上的传承》集,
根据题意,得,
解得.
设该影视公司收益为w万元,
则.
,
w随m的增大而增大.
又,
当时,w取最大值,此时.
答:制作《希望的田野》36集,《指尖上的传承》24集时,该影视公司收益最大.
25.【考点】用勾股定理解三角形、利用平行四边形性质和判定证明
【分析】本题考查了平行四边形的判定与性质,勾股定理,熟记各性质与判定是解题的关键.
(1)先证明,再根据对角线互相平分的四边形是平行四边形进行证明即可;
(2)根据勾股定理求出,再求出,在中,由勾股定理可求出的长.
(1)证明:四边形是平行四边形,
,
又,
,
,
又,
四边形是平行四边形;
(2)解:,
,
在中,由勾股定理得,,
,
,
四边形是平行四边形,
,
在中,由勾股定理得,,
.
26.【考点】等腰三角形的定义、一次函数图象与坐标轴的交点问题、求一次函数解析式
【分析】本题考查的是一次函数综合运用,涉及到等腰三角形的性质、面积的计算等,其中(3),要注意分类求解,避免遗漏.
(1)把点代入直线中得:,则点,直线过点,,;
(2)①由题意得:,,中,当时,,,,,即可求解;②分、、三种情况,分别求解即可.
(1)解:把点代入直线中得:,
点,
直线过点,
,;
(2)解:①由题意得:,
中,当时,,
,
,
中,当时,,
,
,
,
的面积为10,
,
,
则的值7秒;
②设点,点、的坐标为:、,
当时,则点在的中垂线上,即,
解得:;
当时,则点在点的正下方,故,
解得:;
当时,
同理可得:或(舍去)
故:当秒或秒或秒时,为等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
