四边形中的最值 同步练习(含解析)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 四边形中的最值 同步练习(含解析)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 632.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:33:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
四边形中的最值
一、知识梳理
模型介绍——将军饮马模型
1. 如图9-1(a) 所示, 在l上找一点P, 使PA+PB最小.
【分析】如图 9-1(b)所示,作点B关于直线l的对称点B',直线. 与l的交点即为所求点P , PA+PB的最小值为AB'.
2. 如图9-2 (a) 所示, 在l上找一点P , 使 最大.
【分析】如图 9-2(b)所示,直线AB与l的交点即为所求点P , 的最大值为AB.
3. 如图9-3 (a) 所示, 在l上找一点P , 使 最大.
【分析】如图 9-3(b)所示,作点B关于直线l的对称点 直线 与l的交点即为所求点P, 的最大值为.
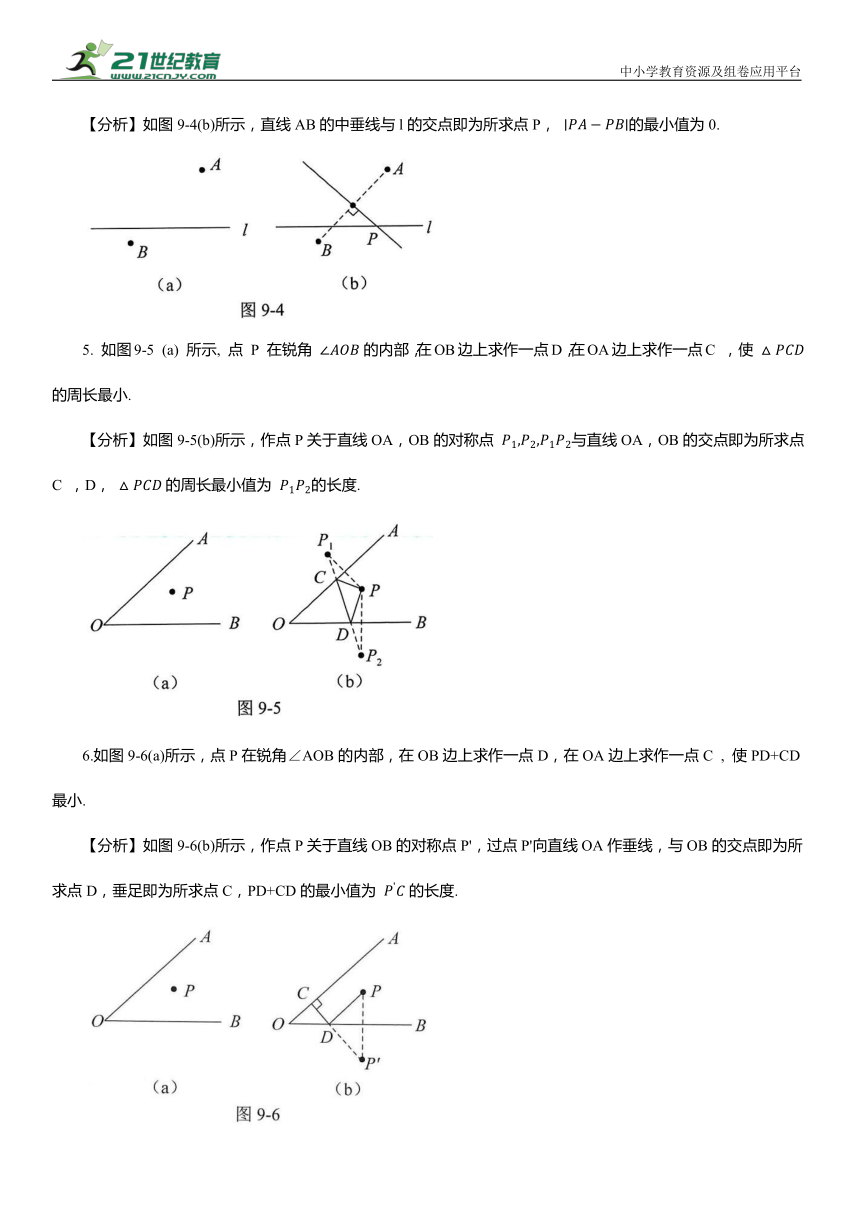
4. 如图9-4 (a) 所示, 在l上找一点P, 使 最小.
【分析】如图9-4(b)所示,直线AB的中垂线与l的交点即为所求点P, 的最小值为0.
5. 如图9-5 (a) 所示, 点 P 在锐角 的内部,在OB边上求作一点D,在OA边上求作一点C , 使 的周长最小.
【分析】如图9-5(b)所示,作点P关于直线OA,OB的对称点 与直线OA,OB的交点即为所求点C ,D, 的周长最小值为 的长度.
6.如图9-6(a)所示,点P在锐角∠AOB的内部,在OB边上求作一点D,在OA边上求作一点C , 使PD+CD最小.
【分析】如图9-6(b)所示,作点P关于直线OB的对称点P',过点P'向直线OA作垂线,与OB的交点即为所求点D,垂足即为所求点C,PD+CD的最小值为 的长度.
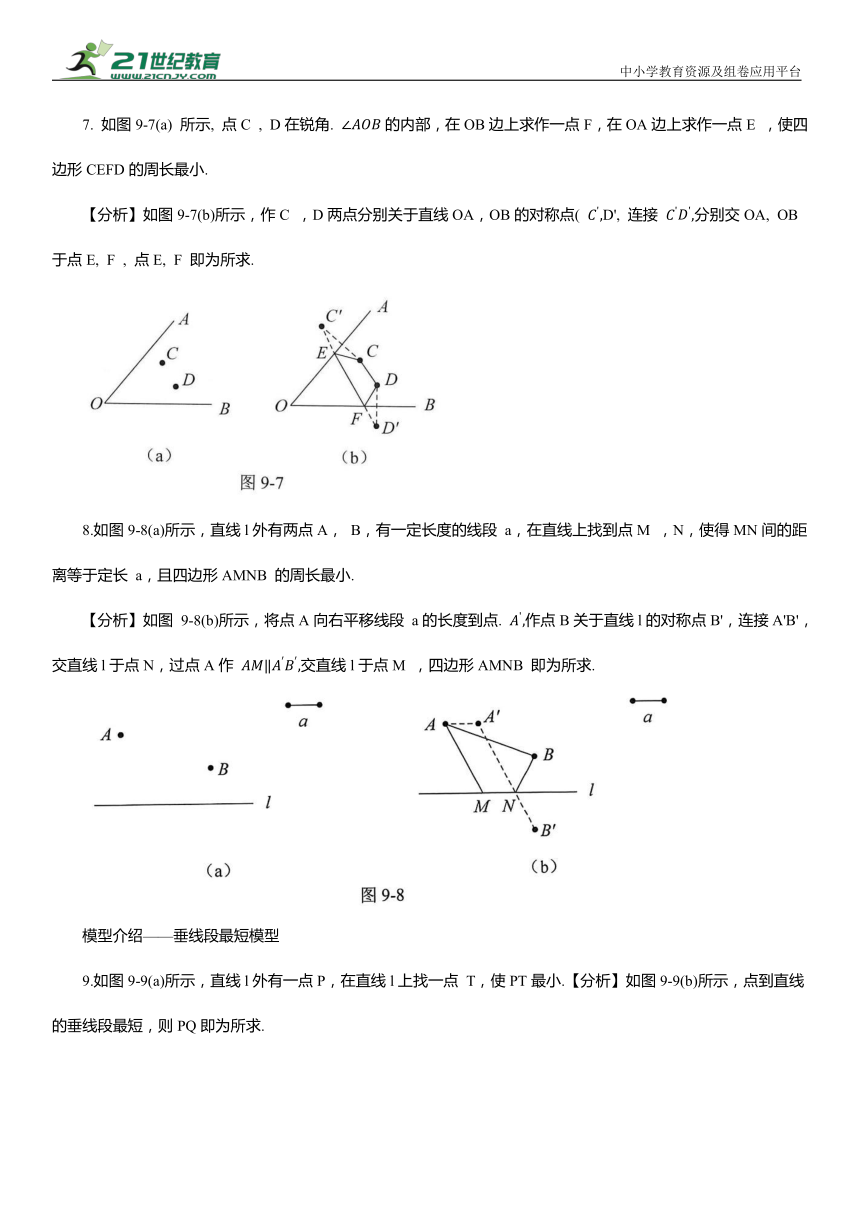
7. 如图9-7(a) 所示, 点C , D在锐角. 的内部,在OB边上求作一点F,在OA边上求作一点E ,使四边形CEFD的周长最小.
【分析】如图9-7(b)所示,作C ,D两点分别关于直线OA,OB的对称点( D', 连接 分别交OA, OB于点E, F , 点E, F 即为所求.
8.如图9-8(a)所示,直线l外有两点A, B,有一定长度的线段 a,在直线上找到点M ,N,使得MN间的距离等于定长 a,且四边形AMNB 的周长最小.
【分析】如图 9-8(b)所示,将点A向右平移线段 a的长度到点. 作点B关于直线l的对称点B',连接A'B',交直线l于点N,过点A作 交直线l于点M ,四边形AMNB 即为所求.
模型介绍——垂线段最短模型
9.如图9-9(a)所示,直线l外有一点P,在直线l上找一点 T,使PT最小.【分析】如图9-9(b)所示,点到直线的垂线段最短,则PQ即为所求.
模型介绍——利用三角形三边关系求最值模型
0.如图9-10所示,点A为动点,AB,BC为定值,求AC的最大值和最小值.
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边,即|AB-BC|≤AC≤AB+BC, 所以AC的最大值为AB+BC, 最小值为|AB-BC|.
二、分层练习
将军饮马模型
1.已知,如图9-11 所示,正方形ABCD的边长为8,点M 在DC上,且DM=2,点N是AC 边上的一个动点,则DN+MN的最小值是 .
2.如图9-12所示, 已知正方形ABCD的边长为6,点E是AB边上的一点,且AE=2, 点P 是AD边上的一个动点, 连接PC, PE, EC, 则 的周长最小值等于 .
3.如图9-13所示,在 中,AB=6,BC=8,∠ABC=60°,点P 是∠ 内的一个动点,且 则PA+PD的最小值为 .
4.如图9-14所示,在菱形ABCD中,点P是对角线BD上的一点,点Q 是BC的中点. 若菱形的周长是16, ∠A=120°, 则. 的最小值为( ).
C. 4
5. 如图9-15 所示, 在矩形ABCD中, AB=3, 对角线AC, BD相交于点O,AE垂直平分OB于点E ,点M ,N分别为AE,AC 上的动点,则 的最小值为( ).
C. 3
6. 如图9-16 所示,在矩形ABCD中, AB=6, AD=5,点P在边AD上,点Q在边BC上,且AP=CQ,连接CP, QD, 则PC+QD的最小值为 .
7.如图9-17所示, AC 是菱形ABCD的对角线,∠ABC=120°,点E , F 是AC上的动点,且 若AD=2, 则DE+BF的最小值为 ( ).
C. 2
8. 如图9-18所示, 在正方形ABCD中, AB=8, AC与BD相交于点O, 点N是AO的中点, 点M 在BC边上,且BM=6, 点P 为对角线BD上的一点, 则PM-PN的最大值为 .
9. (1) 如图9-19 (a) 所示, 点P , Q为△ABC的边AB,AC 上的两个定点,在BC上求作一点M ,使△PQM 的周长最短;(不写作法)
(2)如图9-19(b)所示, 在矩形ABCD中, AB=6, AD=8,点E, F分别为边AB, AD的中点,点M , N分别为BC, CD上的动点,求四边形EFNM 周长的最小值;
(3)如图9-19(c) 所示, 正方形ABCD的边长为2, 点O为AB边的中点,在边AD, CD, BC上分别确定点M , N, P , 使得四边形OMNP的周长最小,并求出最小值.
垂线段最短模型
10. 如图9-20所示, 在△ABC中, . 点D在AB边上, DE⊥AC, DF⊥BC, 垂足分别为点E, F, 连接EF,则线段EF的最小值等于 .
11. 如图9-21 所示, 已知 的顶点A,C分别在直线 和 上,点O 是坐标原点,则对角线OB的最小值为 .
12. 如图9-22 所示, 在. 中, 点P为AB边上的一个动点, 以PA, PC为边作. ,则对角线PQ的最小值为 .
13. 如图9-23 所示, 在 中, 且 点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E , 于点F,点G为四边形DEAF 对角线的交点,则线段GF 的最小值为 .
利用三角形三边关系求最值
14. 如图9-24 所示, 矩形ABCD的顶点A, B 分别在边OM ,ON 上,当点B在边ON上运动时,点A随之在OM 上运动,矩形ABCD的形状保持不变,其中AB=6, BC=2,在运动过程中, 点D到点O的最大距离是 .
15.如图9-25所示,四边形ABCD是矩形,点E是边AB上的一个动点,连接DE, 点A与点P 关于DE对称,连接EP, DP, BP.若. 则BP的最小值为 .
将军饮马模型
1. 解: ∵四边形ABCD是正方形,
∴点B, D关于AC 对称.
∴BN=DN .
∴DN+MN=BN+MN≥BM ,
解题方法详解
如图61所示, 当B, N, M 三点共线时, 的值最小.
∵正方形ABCD的边长是8, DM=2,
∴CM=6.
∵在Rt△BCM 中,
∴ DN+MN的最小值为10.
2.解:如图62所示,作点E关于AD的对称点E',连接CE'交AD于点P.
∵点E, E'关于AD对称,
∴PE=PE'.
∴PE+PC≥E'C.
∴△PCE 的周长=
∴当E'、 P、 C三点共线时, △PCE的周长最小,值为E'C+EC.
∵AE=2, AB=6,
∴BE=4.
∴在Rt△BCE'中, 在Rt△BEC中,
∴△PCE 周长的最小值是
3.解:如图63所示,过点P作直线l∥AD,作点A关于l的对称点A',连接AA', 交l于点E , 交BC于点F , 连接A'P, 则. AA'⊥BC.
∵A'P=AP,
∴AP+PD≥A'D, 当A', P, D三点在同一直线上时,AP+PD的最小值等于A'D的长.
∵AB=6, ∠ABC=60°,
又:
∵四边形ABCD是平行四边形, BC=8,
∴AD=8.
∴在Rt△AA'D中,
∴PA+PD的最小值为
4. 解: 如图64所示, 连接AP, AC, AQ.
∵四边形ABCD是菱形,
∴点A 和点 C关于 BD 对称.
∴AP=CP.
∴PC+PQ=AP+PQ, PC+PQ的最小值即为AP+PQ的最小值.
∵AP+PQ≥AQ,
∴PC+PQ的最小值为AQ.
∵∠BAD=120°, 四边形ABCD 为菱形,
∴∠ABC=60°, AB=AC.
∴△ABC为等边三角形.
∵点Q为BC的中点,
∴AQ⊥BC.
∵菱形ABCD的周长是16,
∴AB=BC=4, BQ=2.
故选B.
5. 解: 如图65所示, 过点B作BN'⊥OA于点N', 交AE于点
∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE 垂直平分OB 于点E,
∴OA=AB.
∴OA=OB=AB.
∴△OAB 是等边三角形.
∵点O与点B关于AE对称,
∴MO+MN的最小值为(
∵△OAB是等边三角形, 且AB=3,
故选 B.
6.解: 如图66所示,在BA的延长线上截取 , 连接BP, PE, CE.
∵四边形ABCD是矩形,
∴AD∥BC, AD=BC.
∵AP=CQ,
∴AD-AP=BC-CQ, 即DP=QB.
又∵ DP∥BQ,
∴四边形DPBQ是平行四边形.
∴PB∥DQ, PB=DQ.
∴PC+QD=PC+PB, PC+QD的最小值转化为PC+PB的最小值.
∵PA⊥BE, AE=AB,
∴PA是BE的垂直平分线.
∴PB=PE.
∴PC+PB=PC+PE.
∵BE=2AB=12, BC=AD=5,
∴PC+PB的最小值为13.
7.解:如图67所示,连接BD交AC于点O,以EF , BF为邻边作平行四边形BFEG.
∵四边形BFEG为平行四边形,
∴DE+BF=DE+EG≥DG.
∴∠DAB=60°.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠AOD=90°.
∴∠GBD=90°.
∴ DE+BF的最小值为
故选D.
8.解:如图68所示, 以BD为对称轴作点N的对称点. 连接 并延长交BD于点P, 连NP.
∵点N , N'关于BD对称,
∴PN=PN'.
∴PM-PN≤MN',
当P,M , N'三点共线时, PM-PN 取最大值.
∵正方形的边长为8,
∵点O为AC的中点,
∵点N 为OA的中点,
∵BM=6,
∴CM=BC-BM=8-6=2.
∴PM∥AB∥CD, ∠CMN'=90°.
∵∠N'CM =45°,
∴△N'CM 为等腰直角三角形.
即PM-PN的最大值为2.
9. 解:(1)如图69所示, 作点P关于BC的对称点P', 连接P'Q, 交BC于点M , 连接PQ, PM, MQ, 则PM=P'M .
∵PM=P'M,
∴△PQM 的最短周长:
∴点M 即为所求.
(2)如图70所示,作点E关于BC的对称点E',作点F关于CD的对称点F',连接 与BC,CD的交点即为四边形EFNM 周长最小时点M、N的位置, 连接EM, FN , 则
∵EM=E'M , FN=F'N,
∴EF+EM+MN+FN =EF+E'M+MN+F'N
∴四边形EFNM 周长的最小值为EF+E'F'的长.
∵AB=6, AD=8,
点E, F 分别为边AB, AD的中点,
∴在Rt△AE'F'中,
又∵在Rt△AEF中,
∴四边形EFNM 周长的最小值:
(3)如图71所示,作点O关于AD的对称点( ,关于BC的对称点( 作点O 关于CD的对称点O ,连接( 则
当N, P , O 点在同一直线上时,
当O , M , N , O 在同一直线上时,
∵正方形边长为2, 点O为AB边的中点,
∴四边形OMNP 周长的最小值为
垂线段最短模型
10. 解: 如图72所示, 连接CD.
∵∠ACB=90°, AC=6, BC=8,
∵DE⊥AC, DF⊥BC, ∠ACB=90°,
∴四边形CFDE是矩形.
∴EF=CD, 由垂线段最短可知,
CD⊥AB时, 线段EF 的值最小.
∴CD=4.8.
∴EF=4.8.
11. 解: 过点B作BD⊥直线x=4, 交直线x=4于点D, 过点B作 轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,直线. 与AB交于点N,如图73所示.
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO, OC∥AB, OA=BC.
∵直线x=1与直线x=4均垂直于x轴,
∴AM∥CN.
∴四边形ANCM 是平行四边形.
∴∠MAN =∠NCM .
∴∠OAF=∠BCD.
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC.
在△OAF和△BCD中,
∴△OAF≌△BCD(ASA).
∴BD=OF =1.
∴OE=4+1=5.
由于OE的长不变,所以当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=5.
12. 解: 设AC , PQ相交于点O, 过点O作( 于点P',如图74所示.
∵四边形PAQC是平行四边形,
∴AO=CO, OP=OQ, PO最短时, PQ最短.
∴△AP'O 是等腰直角三角形.
∴PQ的最小值:
13. 解: 连接AD, EF, 交于点G, 如图75所示.
∵∠BAC=90°, BA=12, AC=16,
∵DE⊥AB, DF⊥AC,
∴∠DEA=∠DFA=∠BAC=90°.
∴四边形DEAF 是矩形.
∴EF=AD.
∴当AD⊥BC时, AD的值最小,此时, △ABC的面积
∴12×16=20AD, 解得
∴EF 的最小值为
∵点G为矩形DEAF对角线的交点,
利用三角形三边关系求最值
14. 解: 如图76所示, 取线段AB的中点E, 连接OE, DE, OD.
∵AB=6, 点E是AB的中点, ∠AOB=90°,
∴AE=BE=OE=3.
∵四边形ABCD是矩形,
∴AD=BC=2, ∠DAB=90°.
∵OD≤OE+DE,
∴当点D, E, O共线时, OD 的长度最大.
∴点D到点O的最大距离
15. 解: 如图77所示, 连接BD, AP.
∵四边形ABCD是矩形,
∴∠A=90°.
∵AB=3, AD=5,
∵点A与点P关于DE对称,
∴DE垂直平分AP.
∴PD=AD=5.
∵BP+PD≥BD,
∴BP的最小值为
四边形中的最值
一、知识梳理
模型介绍——将军饮马模型
1. 如图9-1(a) 所示, 在l上找一点P, 使PA+PB最小.
【分析】如图 9-1(b)所示,作点B关于直线l的对称点B',直线. 与l的交点即为所求点P , PA+PB的最小值为AB'.
2. 如图9-2 (a) 所示, 在l上找一点P , 使 最大.
【分析】如图 9-2(b)所示,直线AB与l的交点即为所求点P , 的最大值为AB.
3. 如图9-3 (a) 所示, 在l上找一点P , 使 最大.
【分析】如图 9-3(b)所示,作点B关于直线l的对称点 直线 与l的交点即为所求点P, 的最大值为.
4. 如图9-4 (a) 所示, 在l上找一点P, 使 最小.
【分析】如图9-4(b)所示,直线AB的中垂线与l的交点即为所求点P, 的最小值为0.
5. 如图9-5 (a) 所示, 点 P 在锐角 的内部,在OB边上求作一点D,在OA边上求作一点C , 使 的周长最小.
【分析】如图9-5(b)所示,作点P关于直线OA,OB的对称点 与直线OA,OB的交点即为所求点C ,D, 的周长最小值为 的长度.
6.如图9-6(a)所示,点P在锐角∠AOB的内部,在OB边上求作一点D,在OA边上求作一点C , 使PD+CD最小.
【分析】如图9-6(b)所示,作点P关于直线OB的对称点P',过点P'向直线OA作垂线,与OB的交点即为所求点D,垂足即为所求点C,PD+CD的最小值为 的长度.
7. 如图9-7(a) 所示, 点C , D在锐角. 的内部,在OB边上求作一点F,在OA边上求作一点E ,使四边形CEFD的周长最小.
【分析】如图9-7(b)所示,作C ,D两点分别关于直线OA,OB的对称点( D', 连接 分别交OA, OB于点E, F , 点E, F 即为所求.
8.如图9-8(a)所示,直线l外有两点A, B,有一定长度的线段 a,在直线上找到点M ,N,使得MN间的距离等于定长 a,且四边形AMNB 的周长最小.
【分析】如图 9-8(b)所示,将点A向右平移线段 a的长度到点. 作点B关于直线l的对称点B',连接A'B',交直线l于点N,过点A作 交直线l于点M ,四边形AMNB 即为所求.
模型介绍——垂线段最短模型
9.如图9-9(a)所示,直线l外有一点P,在直线l上找一点 T,使PT最小.【分析】如图9-9(b)所示,点到直线的垂线段最短,则PQ即为所求.
模型介绍——利用三角形三边关系求最值模型
0.如图9-10所示,点A为动点,AB,BC为定值,求AC的最大值和最小值.
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边,即|AB-BC|≤AC≤AB+BC, 所以AC的最大值为AB+BC, 最小值为|AB-BC|.
二、分层练习
将军饮马模型
1.已知,如图9-11 所示,正方形ABCD的边长为8,点M 在DC上,且DM=2,点N是AC 边上的一个动点,则DN+MN的最小值是 .
2.如图9-12所示, 已知正方形ABCD的边长为6,点E是AB边上的一点,且AE=2, 点P 是AD边上的一个动点, 连接PC, PE, EC, 则 的周长最小值等于 .
3.如图9-13所示,在 中,AB=6,BC=8,∠ABC=60°,点P 是∠ 内的一个动点,且 则PA+PD的最小值为 .
4.如图9-14所示,在菱形ABCD中,点P是对角线BD上的一点,点Q 是BC的中点. 若菱形的周长是16, ∠A=120°, 则. 的最小值为( ).
C. 4
5. 如图9-15 所示, 在矩形ABCD中, AB=3, 对角线AC, BD相交于点O,AE垂直平分OB于点E ,点M ,N分别为AE,AC 上的动点,则 的最小值为( ).
C. 3
6. 如图9-16 所示,在矩形ABCD中, AB=6, AD=5,点P在边AD上,点Q在边BC上,且AP=CQ,连接CP, QD, 则PC+QD的最小值为 .
7.如图9-17所示, AC 是菱形ABCD的对角线,∠ABC=120°,点E , F 是AC上的动点,且 若AD=2, 则DE+BF的最小值为 ( ).
C. 2
8. 如图9-18所示, 在正方形ABCD中, AB=8, AC与BD相交于点O, 点N是AO的中点, 点M 在BC边上,且BM=6, 点P 为对角线BD上的一点, 则PM-PN的最大值为 .
9. (1) 如图9-19 (a) 所示, 点P , Q为△ABC的边AB,AC 上的两个定点,在BC上求作一点M ,使△PQM 的周长最短;(不写作法)
(2)如图9-19(b)所示, 在矩形ABCD中, AB=6, AD=8,点E, F分别为边AB, AD的中点,点M , N分别为BC, CD上的动点,求四边形EFNM 周长的最小值;
(3)如图9-19(c) 所示, 正方形ABCD的边长为2, 点O为AB边的中点,在边AD, CD, BC上分别确定点M , N, P , 使得四边形OMNP的周长最小,并求出最小值.
垂线段最短模型
10. 如图9-20所示, 在△ABC中, . 点D在AB边上, DE⊥AC, DF⊥BC, 垂足分别为点E, F, 连接EF,则线段EF的最小值等于 .
11. 如图9-21 所示, 已知 的顶点A,C分别在直线 和 上,点O 是坐标原点,则对角线OB的最小值为 .
12. 如图9-22 所示, 在. 中, 点P为AB边上的一个动点, 以PA, PC为边作. ,则对角线PQ的最小值为 .
13. 如图9-23 所示, 在 中, 且 点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E , 于点F,点G为四边形DEAF 对角线的交点,则线段GF 的最小值为 .
利用三角形三边关系求最值
14. 如图9-24 所示, 矩形ABCD的顶点A, B 分别在边OM ,ON 上,当点B在边ON上运动时,点A随之在OM 上运动,矩形ABCD的形状保持不变,其中AB=6, BC=2,在运动过程中, 点D到点O的最大距离是 .
15.如图9-25所示,四边形ABCD是矩形,点E是边AB上的一个动点,连接DE, 点A与点P 关于DE对称,连接EP, DP, BP.若. 则BP的最小值为 .
将军饮马模型
1. 解: ∵四边形ABCD是正方形,
∴点B, D关于AC 对称.
∴BN=DN .
∴DN+MN=BN+MN≥BM ,
解题方法详解
如图61所示, 当B, N, M 三点共线时, 的值最小.
∵正方形ABCD的边长是8, DM=2,
∴CM=6.
∵在Rt△BCM 中,
∴ DN+MN的最小值为10.
2.解:如图62所示,作点E关于AD的对称点E',连接CE'交AD于点P.
∵点E, E'关于AD对称,
∴PE=PE'.
∴PE+PC≥E'C.
∴△PCE 的周长=
∴当E'、 P、 C三点共线时, △PCE的周长最小,值为E'C+EC.
∵AE=2, AB=6,
∴BE=4.
∴在Rt△BCE'中, 在Rt△BEC中,
∴△PCE 周长的最小值是
3.解:如图63所示,过点P作直线l∥AD,作点A关于l的对称点A',连接AA', 交l于点E , 交BC于点F , 连接A'P, 则. AA'⊥BC.
∵A'P=AP,
∴AP+PD≥A'D, 当A', P, D三点在同一直线上时,AP+PD的最小值等于A'D的长.
∵AB=6, ∠ABC=60°,
又:
∵四边形ABCD是平行四边形, BC=8,
∴AD=8.
∴在Rt△AA'D中,
∴PA+PD的最小值为
4. 解: 如图64所示, 连接AP, AC, AQ.
∵四边形ABCD是菱形,
∴点A 和点 C关于 BD 对称.
∴AP=CP.
∴PC+PQ=AP+PQ, PC+PQ的最小值即为AP+PQ的最小值.
∵AP+PQ≥AQ,
∴PC+PQ的最小值为AQ.
∵∠BAD=120°, 四边形ABCD 为菱形,
∴∠ABC=60°, AB=AC.
∴△ABC为等边三角形.
∵点Q为BC的中点,
∴AQ⊥BC.
∵菱形ABCD的周长是16,
∴AB=BC=4, BQ=2.
故选B.
5. 解: 如图65所示, 过点B作BN'⊥OA于点N', 交AE于点
∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE 垂直平分OB 于点E,
∴OA=AB.
∴OA=OB=AB.
∴△OAB 是等边三角形.
∵点O与点B关于AE对称,
∴MO+MN的最小值为(
∵△OAB是等边三角形, 且AB=3,
故选 B.
6.解: 如图66所示,在BA的延长线上截取 , 连接BP, PE, CE.
∵四边形ABCD是矩形,
∴AD∥BC, AD=BC.
∵AP=CQ,
∴AD-AP=BC-CQ, 即DP=QB.
又∵ DP∥BQ,
∴四边形DPBQ是平行四边形.
∴PB∥DQ, PB=DQ.
∴PC+QD=PC+PB, PC+QD的最小值转化为PC+PB的最小值.
∵PA⊥BE, AE=AB,
∴PA是BE的垂直平分线.
∴PB=PE.
∴PC+PB=PC+PE.
∵BE=2AB=12, BC=AD=5,
∴PC+PB的最小值为13.
7.解:如图67所示,连接BD交AC于点O,以EF , BF为邻边作平行四边形BFEG.
∵四边形BFEG为平行四边形,
∴DE+BF=DE+EG≥DG.
∴∠DAB=60°.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠AOD=90°.
∴∠GBD=90°.
∴ DE+BF的最小值为
故选D.
8.解:如图68所示, 以BD为对称轴作点N的对称点. 连接 并延长交BD于点P, 连NP.
∵点N , N'关于BD对称,
∴PN=PN'.
∴PM-PN≤MN',
当P,M , N'三点共线时, PM-PN 取最大值.
∵正方形的边长为8,
∵点O为AC的中点,
∵点N 为OA的中点,
∵BM=6,
∴CM=BC-BM=8-6=2.
∴PM∥AB∥CD, ∠CMN'=90°.
∵∠N'CM =45°,
∴△N'CM 为等腰直角三角形.
即PM-PN的最大值为2.
9. 解:(1)如图69所示, 作点P关于BC的对称点P', 连接P'Q, 交BC于点M , 连接PQ, PM, MQ, 则PM=P'M .
∵PM=P'M,
∴△PQM 的最短周长:
∴点M 即为所求.
(2)如图70所示,作点E关于BC的对称点E',作点F关于CD的对称点F',连接 与BC,CD的交点即为四边形EFNM 周长最小时点M、N的位置, 连接EM, FN , 则
∵EM=E'M , FN=F'N,
∴EF+EM+MN+FN =EF+E'M+MN+F'N
∴四边形EFNM 周长的最小值为EF+E'F'的长.
∵AB=6, AD=8,
点E, F 分别为边AB, AD的中点,
∴在Rt△AE'F'中,
又∵在Rt△AEF中,
∴四边形EFNM 周长的最小值:
(3)如图71所示,作点O关于AD的对称点( ,关于BC的对称点( 作点O 关于CD的对称点O ,连接( 则
当N, P , O 点在同一直线上时,
当O , M , N , O 在同一直线上时,
∵正方形边长为2, 点O为AB边的中点,
∴四边形OMNP 周长的最小值为
垂线段最短模型
10. 解: 如图72所示, 连接CD.
∵∠ACB=90°, AC=6, BC=8,
∵DE⊥AC, DF⊥BC, ∠ACB=90°,
∴四边形CFDE是矩形.
∴EF=CD, 由垂线段最短可知,
CD⊥AB时, 线段EF 的值最小.
∴CD=4.8.
∴EF=4.8.
11. 解: 过点B作BD⊥直线x=4, 交直线x=4于点D, 过点B作 轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,直线. 与AB交于点N,如图73所示.
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO, OC∥AB, OA=BC.
∵直线x=1与直线x=4均垂直于x轴,
∴AM∥CN.
∴四边形ANCM 是平行四边形.
∴∠MAN =∠NCM .
∴∠OAF=∠BCD.
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC.
在△OAF和△BCD中,
∴△OAF≌△BCD(ASA).
∴BD=OF =1.
∴OE=4+1=5.
由于OE的长不变,所以当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=5.
12. 解: 设AC , PQ相交于点O, 过点O作( 于点P',如图74所示.
∵四边形PAQC是平行四边形,
∴AO=CO, OP=OQ, PO最短时, PQ最短.
∴△AP'O 是等腰直角三角形.
∴PQ的最小值:
13. 解: 连接AD, EF, 交于点G, 如图75所示.
∵∠BAC=90°, BA=12, AC=16,
∵DE⊥AB, DF⊥AC,
∴∠DEA=∠DFA=∠BAC=90°.
∴四边形DEAF 是矩形.
∴EF=AD.
∴当AD⊥BC时, AD的值最小,此时, △ABC的面积
∴12×16=20AD, 解得
∴EF 的最小值为
∵点G为矩形DEAF对角线的交点,
利用三角形三边关系求最值
14. 解: 如图76所示, 取线段AB的中点E, 连接OE, DE, OD.
∵AB=6, 点E是AB的中点, ∠AOB=90°,
∴AE=BE=OE=3.
∵四边形ABCD是矩形,
∴AD=BC=2, ∠DAB=90°.
∵OD≤OE+DE,
∴当点D, E, O共线时, OD 的长度最大.
∴点D到点O的最大距离
15. 解: 如图77所示, 连接BD, AP.
∵四边形ABCD是矩形,
∴∠A=90°.
∵AB=3, AD=5,
∵点A与点P关于DE对称,
∴DE垂直平分AP.
∴PD=AD=5.
∵BP+PD≥BD,
∴BP的最小值为
