四边形综合 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 四边形综合 同步练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 313.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:35:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
四边形综合
1.如图10-1所示,在正方形ABCD中,点E是AB上一点,点F在BC的延长线上, 且AE=CF, 连接DE, DF, EF, BD, EF交CD于点 G, 下列结论正确的是 ( ).
① ∠DEF=45°;
② △BCD≌△EDF;
③ 若 则 S△DEF=5;
④ 若点E为AB的中点,则
A. ①② B. ①③ C. ①③④ D. ②③
2.如图10-2所示,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中, 点A(10, 0), 点B(0, 6), 点P 为BC边上的动点, 将 沿OP 折叠得到△OPD,连接CD, AD, 则下列结论中正确的有 ( ).
① 当∠BOP=45°时, 四边形OBPD 为正方形;
② 当∠BOP=30°时, △OAD的面积为15;
③ 当OD⊥AD时, BP=2.
A. 0个
B. 1个
C. 2个
D. 3个
3.如图10-3所示,正方形ABCD的边长为4,点E在边DC 上运动(不含端点),以AE为边作等腰直角三角形AEF , ∠AEF=90°,连接DF,则下面四个说法中正确的有 ( ).
① 当DE=1时,
② 当DE=2时, 点B , D, F 共线;
③ 当△ADF 与△EDF 面积相等时,
④ 当AD平分∠EAF时,
A. 1个 B. 2个
C. 3个 D. 4个
4.如图10-4所示,已知正方形ABCD的边长为2,点P 是对角线BD上的一点,PE⊥BC于点E, PF⊥CD于点F, 连接AP, EF , 下列结论正确的个数有( ).
② 四边形PECF 的周长为4;
③ △APD一定是等腰三角形;
④ AP⊥EF且AP=EF;
⑤ EF 的最小值为
A. 2个
B. 3个
C. 4个
D. 5个
5.如图10-5所示,在边长为 的菱形ABCD中,点F为边AD的中点,BF 与对角线AC交于点G, 过点G作GE⊥AB于点E, 且. 则以下结论正确的是 ( ).
① BF⊥AD;
② ∠BAD=60°;
③ CG=2AG;
④ S△ADC是S△AGB的. 倍;
⑤ 若点H为AC上的一动点, 连接DH ,FH , 则DH+FH 的最小值为3.
A. ①③⑤
B. ②③④
C. ①②④⑤
D. ①②③⑤
6.如图10-6所示,正方形ABCD的边长为4,点E是对角线AC上的动点(点E不与点A, C重合), 连接BE, 交CD于点 F,线段EF绕点F逆时针旋转90°得到线段FG,连接BG,CG,下列结论正确的是 .(填写所有正确结论的序号)
① BE=EF;
② ∠ACG=90°;
③ 若四边形BEFG的面积是正方形ABCD面积的一半,AE 的长为
7.在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合,如图10-7(a)所示,其中∠ACB=∠DFE=90°, BC=EF =3cm, AC=DF=4cm,并进行如下研究活动.
活动一: 将图10-7 (a) 中的纸片DEF沿AC方向平移, 连接AE, BD, 如图10-7(b)所示, 当点F 与点C 重合时停止平移.
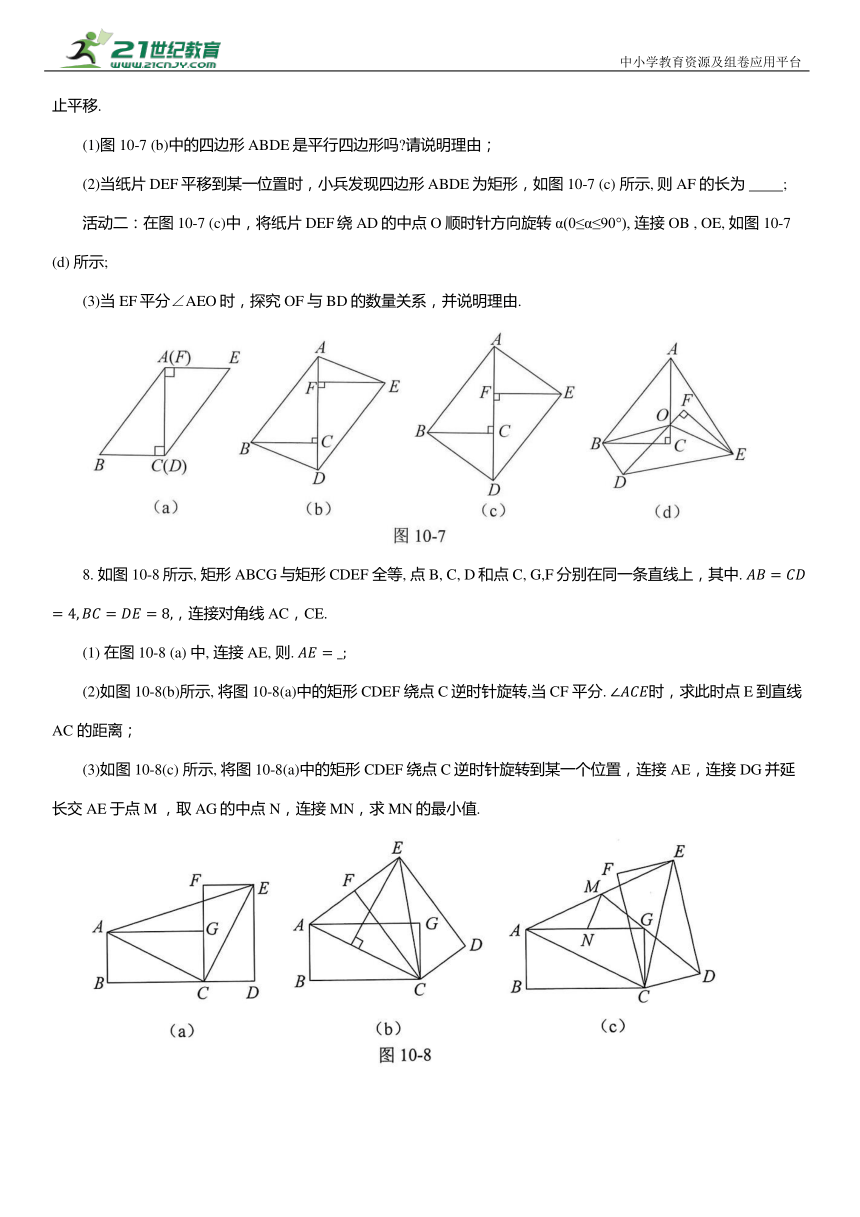
(1)图10-7 (b)中的四边形ABDE是平行四边形吗 请说明理由;
(2)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形,如图10-7 (c) 所示, 则AF 的长为 ;
活动二:在图 10-7 (c)中,将纸片DEF绕AD的中点O 顺时针方向旋转α(0≤α≤90°), 连接OB , OE, 如图10-7(d) 所示;
(3)当EF平分∠AEO时,探究OF 与BD的数量关系,并说明理由.
8. 如图10-8所示, 矩形ABCG与矩形CDEF 全等, 点B, C, D和点C, G,F分别在同一条直线上,其中. ,连接对角线AC,CE.
(1) 在图10-8 (a) 中, 连接AE, 则.
(2)如图10-8(b)所示, 将图10-8(a)中的矩形CDEF 绕点C逆时针旋转,当CF 平分. 时,求此时点E到直线AC 的距离;
(3)如图10-8(c) 所示, 将图10-8(a)中的矩形CDEF 绕点C逆时针旋转到某一个位置,连接AE,连接DG并延长交AE于点M ,取AG的中点N,连接MN,求MN的最小值.
1. 解: ∵四边形ABCD 是正方形,
∴AB=CD=BC=DA,
∠DAE=∠BCD=90°. ∴AE=1.
∴∠DAE=∠DCF.
又∵AE=CF,
∴△ADE≌△CDF (SAS).
∴DE=DF, ∠ADE=∠CDF. 故③正确.
∵∠ADE+∠EDC=90°, 设AB=BC=AD=2a,则
∴∠CDF+∠EDC=90°. ∵点E为AB的中点,
∴∠EDF=90°. ∴AE=a.
∴∠DEF=∠DFE=45°,
故①正确.
∵DE=DF≠DC,
∴△BCD和△EDF不全等,
故②错误.
2. 解: ①∵四边形OACB 是矩形,
∴∠OBC=90°.
∵将△OBP沿OP 折叠得到△OPD,
∴OB=OD, ∠PDO=∠OBP=90°, ∠BOP=∠DOP.
∵∠BOP=45°,
∴∠DOP=∠BOP=45°.
∴∠BOD=90°.
∴∠BOD=∠OBP=∠ODP=90°.
∴四边形OBPD 是矩形.
∵OB=OD,
∴四边形OBPD为正方形,故①正确.
② 过点D作DH⊥OA于点H, 如图78所示.
∵点A(10, 0), 点B(0, 6),
∴OA=10, OB=6.
∴OD=OB=6, ∠BOP=∠DOP=30°.
∴∠DOA=30°.
∴△OAD的面积 故②正确.
③ ∵OD⊥AD,
∴∠ADO=90°.
∵∠ODP=∠OBP=90°,
∴P, D, A三点共线.
∵OA∥BC,
∴∠OPB=∠POA.
∵∠OPB=∠OPD,
∴∠OPA=∠POA.
∴AP=OA=10.
∵AC=6,
∴BP=BC-CP=10-8=2, 故③正确.
故选 D.
3. 解: 当DE=1时,
∵△AEF是等腰直角三角形,
故①说法正确.
当DE=2时, 如图79所示, 过点F作FH⊥CD, 交CD的延长线于点H.
∵△AEF是等腰直角三角形, ∠AEF =90°,
∴AE=EF.
∴∠AED+∠FEH =90°.
∵∠AED+∠DAE=90°,
∴∠DAE=∠FEH.
在△AED和△EFH中,
∴△AED≌△EFH(AAS).
∴HE=AD=4, HF=DE=2.
∴DH=4-2=2=HF.
∴∠HDF=45°.
∵∠HDF+∠ADH+∠ADB=180°,
∴B, D, F三点共线, 故②说法正确.
∵△AED≌△EFH,
∴DE=HF, AD=HE=4.
∴HD=4-DE.
∵三角形ADF与三角形EDF 面积相等,
即
或 (舍去),故③说法正确.
如图80所示, 在AD上截取DN=DE , 连接NE .
∵∠ADC=90°, DN=DE,
∵AD平分∠EAF,
∴∠DAE=22.5°.
∴∠AEN=∠DNE-∠DAE=22.5°.
∴∠AEN =∠DAE .
∵AN+DN=AD=4,
故④说法错误.
故选C.
4. 解: 如图81所示, 延长FP交AB于点G, 连接PC,延长AP交EF于点H.
∵GF∥BC,
∴∠DPF =∠DBC.
∵四边形ABCD是正方形,
∴∠DBC=45°.
∴∠DPF=∠DBC=45°.
∴∠PDF=∠DPF=45°.
∴PF=EC=DF , BE=PE.
∵在Rt△DPF中,
故①正确.
∵PE⊥BC, PF⊥CD, ∠BCD=90°,
∴四边形PECF为矩形.
∴四边形PECF 的周长=2CE+2PE=2CE+2BE=2BC=4, 故②正确.
∵点P是正方形ABCD对角线BD上的任意一点,
∴只有当∠PAD=45°或∠PAD=67.5°或∠PAD=90°时,△APD是等腰三角形,故③错误.
∵四边形PECF 为矩形,
∴PC=EF.
∵四边形ABCD为正方形,点P 为对角线BD上的一点,
∴AP=PC.
∴AP=EF.
∵BD平分∠ABC, PG⊥AB, PE⊥BC,
∴PG=PE.
∵AP=PC , ∠AGP=∠EPF=90°,
∴Rt△AGP≌Rt△FPE(HL).
∴∠GAP=∠PFE .
∵∠AGP=90°,
∴∠GAP+∠APG=90°.
∵∠APG=∠HPF ,
∴∠PFH+∠HPF=90°.
∴AP⊥EF , 故④正确.
∵EF=PC=AP,
∴当AP最小时, EF最小.
∵当AP⊥BD时, AP最小,
∴EF 的最小值等于 故⑤正确.
故选C.
5. 解: ∵四边形ABCD是菱形,
∴AD=CD=AB,
∠1=∠DAC=∠BAC.
∵∠1=∠2,
∴∠BAC=∠2.
又∵GE⊥AB,
∵点F为边AD的中点,
∴AF=AE.
又∵∠DAC=∠BAC, AG=AG,
∴△AGF≌△AGE(SAS).
∴FG=GE,∠AFG=∠AEG=90°.
∴BF⊥AD, 故①正确.
如图82所示,连接BH.
∵四边形ABCD是菱形,
∴点D与点B关于AC 对称.
∴DH=BH .
∴DH+FH=BH+FH.
∴当F, H, B三点共线时,DH+FH有最小值, 为BF的长.
∴DH+FH的最小值为3, 故⑤正确.
故选D.
6. 解: 如图83所示, 过点E作EN⊥BC于点N, EH⊥CD于点H.
∵四边形ABCD是正方形,
∴∠ACB=∠ACD=45°, ∠BCD=90°, AC= AB.
又∵EN⊥BC, EH⊥CD,
∴EN=EH, 四边形ENCH 是矩形.
∴∠BEN=∠FEH.
又∵∠ENB=∠EHF=90°,
∴△BEN≌△FEH (ASA).
∴BE=EF, 故①正确.
∵线段 EF绕点 F逆时针旋转90°得到线段 FG,
∴EF=FG, ∠EFG=90°.
∴BE∥GF.
∴四边形 BEFG 是平行四边形.
又∵∠EFG=90°, EF=FG,
∴四边形 BEFG是正方形.
∴BE=BG, ∠EBG=90°.
∴∠EBG=∠ABC=90°.
∴∠ABE=∠CBG.
又∵AB=BC,
∴△ABE≌△CBG(SAS).
故②正确.
故④正确.
∵正方形ABCD的边长为4,
如图84所示,连接EG.
∵四边形BEFG是正方形,
故③错误.
故答案为①②④.
7. 解: (1) 四边形ABDE是平行四边形.
理由: ∵△ABC≌△DEF ,
∴AB=DE, ∠BAC=∠EDF.
∴AB∥DE.
∴四边形ABDE是平行四边形.
(2) 如图85所示, 连接BE交AD于点O.
∵四边形ABDE为矩形,
∴OA=OD=OB=OE.
设AF = xcm, 则
∵在Rt△OFE中,
即
(3) BD=2OF.
理由:如图86所示,延长OF 交AE于点H.
∵由矩形的性质及旋转的性质知, OA=OB=OE=OD,
∴∠OAB=∠OBA=∠ODE=∠OED, ∠OBD=∠ODB, ∠OAE=∠OEA.
∴∠BDE+∠DEA=∠ABD+∠EAB.
∵∠ABD+∠BDE+∠DEA+∠EAB=360°,
∴∠ABD+∠EAB=180°.
∴AE∥BD.
∴∠OHE=∠ODB .
∵EF平分∠AEO,
∴∠OEF =∠HEF.
∵∠EFO=∠EFH=90°, EF=EF,
∴△EFO≌△EFH(ASA).
∴EO=EH, FO=FH.
∴∠EHO=∠EOH =∠OBD=∠ODB.
∴△EOH≌△OBD(AAS).
∴BD=OH=2OF.
8. 解: (1) ∵矩形ABCG与矩形CDEF全等,
∴AC=CE, ∠ACB=∠ECF .
∵∠ACB+∠ACG=90°,
∴∠ACE=90°.
(2) ∵AC=CE, CF平分∠ACE,
∴由等腰三角形“三线合一”得, CF⊥AE, AF=EF=4.
设点E到直线AC的距离为d.
∴此时点E到直线AC 的距离为
(3)如图87所示,过点E作AG的平行线交DM 的延长线于点H,连接EG.
∵HE∥AG,
∴∠H=∠MGA.
∵CG=CD,
∴∠CGD=∠CDG.
∵∠AGC=∠CDE=90°,
∴∠MGA+∠CGD=90°, ∠CDG+∠HDE=90°.
∴∠MGA=∠HDE.
∴∠HDE=∠H .
∴HE =ED=AG.
在△HME与△GMA中,
∴△HME≌△GMA(AAS).
∴AM=ME.
∵AG的中点为点N,
∵ 在矩形 CDEF 绕 点 C 逆时 针旋转 的过程中 , GE 的 范围为
∴GE的最小值为
∴MN的最小值为
四边形综合
1.如图10-1所示,在正方形ABCD中,点E是AB上一点,点F在BC的延长线上, 且AE=CF, 连接DE, DF, EF, BD, EF交CD于点 G, 下列结论正确的是 ( ).
① ∠DEF=45°;
② △BCD≌△EDF;
③ 若 则 S△DEF=5;
④ 若点E为AB的中点,则
A. ①② B. ①③ C. ①③④ D. ②③
2.如图10-2所示,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中, 点A(10, 0), 点B(0, 6), 点P 为BC边上的动点, 将 沿OP 折叠得到△OPD,连接CD, AD, 则下列结论中正确的有 ( ).
① 当∠BOP=45°时, 四边形OBPD 为正方形;
② 当∠BOP=30°时, △OAD的面积为15;
③ 当OD⊥AD时, BP=2.
A. 0个
B. 1个
C. 2个
D. 3个
3.如图10-3所示,正方形ABCD的边长为4,点E在边DC 上运动(不含端点),以AE为边作等腰直角三角形AEF , ∠AEF=90°,连接DF,则下面四个说法中正确的有 ( ).
① 当DE=1时,
② 当DE=2时, 点B , D, F 共线;
③ 当△ADF 与△EDF 面积相等时,
④ 当AD平分∠EAF时,
A. 1个 B. 2个
C. 3个 D. 4个
4.如图10-4所示,已知正方形ABCD的边长为2,点P 是对角线BD上的一点,PE⊥BC于点E, PF⊥CD于点F, 连接AP, EF , 下列结论正确的个数有( ).
② 四边形PECF 的周长为4;
③ △APD一定是等腰三角形;
④ AP⊥EF且AP=EF;
⑤ EF 的最小值为
A. 2个
B. 3个
C. 4个
D. 5个
5.如图10-5所示,在边长为 的菱形ABCD中,点F为边AD的中点,BF 与对角线AC交于点G, 过点G作GE⊥AB于点E, 且. 则以下结论正确的是 ( ).
① BF⊥AD;
② ∠BAD=60°;
③ CG=2AG;
④ S△ADC是S△AGB的. 倍;
⑤ 若点H为AC上的一动点, 连接DH ,FH , 则DH+FH 的最小值为3.
A. ①③⑤
B. ②③④
C. ①②④⑤
D. ①②③⑤
6.如图10-6所示,正方形ABCD的边长为4,点E是对角线AC上的动点(点E不与点A, C重合), 连接BE, 交CD于点 F,线段EF绕点F逆时针旋转90°得到线段FG,连接BG,CG,下列结论正确的是 .(填写所有正确结论的序号)
① BE=EF;
② ∠ACG=90°;
③ 若四边形BEFG的面积是正方形ABCD面积的一半,AE 的长为
7.在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合,如图10-7(a)所示,其中∠ACB=∠DFE=90°, BC=EF =3cm, AC=DF=4cm,并进行如下研究活动.
活动一: 将图10-7 (a) 中的纸片DEF沿AC方向平移, 连接AE, BD, 如图10-7(b)所示, 当点F 与点C 重合时停止平移.
(1)图10-7 (b)中的四边形ABDE是平行四边形吗 请说明理由;
(2)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形,如图10-7 (c) 所示, 则AF 的长为 ;
活动二:在图 10-7 (c)中,将纸片DEF绕AD的中点O 顺时针方向旋转α(0≤α≤90°), 连接OB , OE, 如图10-7(d) 所示;
(3)当EF平分∠AEO时,探究OF 与BD的数量关系,并说明理由.
8. 如图10-8所示, 矩形ABCG与矩形CDEF 全等, 点B, C, D和点C, G,F分别在同一条直线上,其中. ,连接对角线AC,CE.
(1) 在图10-8 (a) 中, 连接AE, 则.
(2)如图10-8(b)所示, 将图10-8(a)中的矩形CDEF 绕点C逆时针旋转,当CF 平分. 时,求此时点E到直线AC 的距离;
(3)如图10-8(c) 所示, 将图10-8(a)中的矩形CDEF 绕点C逆时针旋转到某一个位置,连接AE,连接DG并延长交AE于点M ,取AG的中点N,连接MN,求MN的最小值.
1. 解: ∵四边形ABCD 是正方形,
∴AB=CD=BC=DA,
∠DAE=∠BCD=90°. ∴AE=1.
∴∠DAE=∠DCF.
又∵AE=CF,
∴△ADE≌△CDF (SAS).
∴DE=DF, ∠ADE=∠CDF. 故③正确.
∵∠ADE+∠EDC=90°, 设AB=BC=AD=2a,则
∴∠CDF+∠EDC=90°. ∵点E为AB的中点,
∴∠EDF=90°. ∴AE=a.
∴∠DEF=∠DFE=45°,
故①正确.
∵DE=DF≠DC,
∴△BCD和△EDF不全等,
故②错误.
2. 解: ①∵四边形OACB 是矩形,
∴∠OBC=90°.
∵将△OBP沿OP 折叠得到△OPD,
∴OB=OD, ∠PDO=∠OBP=90°, ∠BOP=∠DOP.
∵∠BOP=45°,
∴∠DOP=∠BOP=45°.
∴∠BOD=90°.
∴∠BOD=∠OBP=∠ODP=90°.
∴四边形OBPD 是矩形.
∵OB=OD,
∴四边形OBPD为正方形,故①正确.
② 过点D作DH⊥OA于点H, 如图78所示.
∵点A(10, 0), 点B(0, 6),
∴OA=10, OB=6.
∴OD=OB=6, ∠BOP=∠DOP=30°.
∴∠DOA=30°.
∴△OAD的面积 故②正确.
③ ∵OD⊥AD,
∴∠ADO=90°.
∵∠ODP=∠OBP=90°,
∴P, D, A三点共线.
∵OA∥BC,
∴∠OPB=∠POA.
∵∠OPB=∠OPD,
∴∠OPA=∠POA.
∴AP=OA=10.
∵AC=6,
∴BP=BC-CP=10-8=2, 故③正确.
故选 D.
3. 解: 当DE=1时,
∵△AEF是等腰直角三角形,
故①说法正确.
当DE=2时, 如图79所示, 过点F作FH⊥CD, 交CD的延长线于点H.
∵△AEF是等腰直角三角形, ∠AEF =90°,
∴AE=EF.
∴∠AED+∠FEH =90°.
∵∠AED+∠DAE=90°,
∴∠DAE=∠FEH.
在△AED和△EFH中,
∴△AED≌△EFH(AAS).
∴HE=AD=4, HF=DE=2.
∴DH=4-2=2=HF.
∴∠HDF=45°.
∵∠HDF+∠ADH+∠ADB=180°,
∴B, D, F三点共线, 故②说法正确.
∵△AED≌△EFH,
∴DE=HF, AD=HE=4.
∴HD=4-DE.
∵三角形ADF与三角形EDF 面积相等,
即
或 (舍去),故③说法正确.
如图80所示, 在AD上截取DN=DE , 连接NE .
∵∠ADC=90°, DN=DE,
∵AD平分∠EAF,
∴∠DAE=22.5°.
∴∠AEN=∠DNE-∠DAE=22.5°.
∴∠AEN =∠DAE .
∵AN+DN=AD=4,
故④说法错误.
故选C.
4. 解: 如图81所示, 延长FP交AB于点G, 连接PC,延长AP交EF于点H.
∵GF∥BC,
∴∠DPF =∠DBC.
∵四边形ABCD是正方形,
∴∠DBC=45°.
∴∠DPF=∠DBC=45°.
∴∠PDF=∠DPF=45°.
∴PF=EC=DF , BE=PE.
∵在Rt△DPF中,
故①正确.
∵PE⊥BC, PF⊥CD, ∠BCD=90°,
∴四边形PECF为矩形.
∴四边形PECF 的周长=2CE+2PE=2CE+2BE=2BC=4, 故②正确.
∵点P是正方形ABCD对角线BD上的任意一点,
∴只有当∠PAD=45°或∠PAD=67.5°或∠PAD=90°时,△APD是等腰三角形,故③错误.
∵四边形PECF 为矩形,
∴PC=EF.
∵四边形ABCD为正方形,点P 为对角线BD上的一点,
∴AP=PC.
∴AP=EF.
∵BD平分∠ABC, PG⊥AB, PE⊥BC,
∴PG=PE.
∵AP=PC , ∠AGP=∠EPF=90°,
∴Rt△AGP≌Rt△FPE(HL).
∴∠GAP=∠PFE .
∵∠AGP=90°,
∴∠GAP+∠APG=90°.
∵∠APG=∠HPF ,
∴∠PFH+∠HPF=90°.
∴AP⊥EF , 故④正确.
∵EF=PC=AP,
∴当AP最小时, EF最小.
∵当AP⊥BD时, AP最小,
∴EF 的最小值等于 故⑤正确.
故选C.
5. 解: ∵四边形ABCD是菱形,
∴AD=CD=AB,
∠1=∠DAC=∠BAC.
∵∠1=∠2,
∴∠BAC=∠2.
又∵GE⊥AB,
∵点F为边AD的中点,
∴AF=AE.
又∵∠DAC=∠BAC, AG=AG,
∴△AGF≌△AGE(SAS).
∴FG=GE,∠AFG=∠AEG=90°.
∴BF⊥AD, 故①正确.
如图82所示,连接BH.
∵四边形ABCD是菱形,
∴点D与点B关于AC 对称.
∴DH=BH .
∴DH+FH=BH+FH.
∴当F, H, B三点共线时,DH+FH有最小值, 为BF的长.
∴DH+FH的最小值为3, 故⑤正确.
故选D.
6. 解: 如图83所示, 过点E作EN⊥BC于点N, EH⊥CD于点H.
∵四边形ABCD是正方形,
∴∠ACB=∠ACD=45°, ∠BCD=90°, AC= AB.
又∵EN⊥BC, EH⊥CD,
∴EN=EH, 四边形ENCH 是矩形.
∴∠BEN=∠FEH.
又∵∠ENB=∠EHF=90°,
∴△BEN≌△FEH (ASA).
∴BE=EF, 故①正确.
∵线段 EF绕点 F逆时针旋转90°得到线段 FG,
∴EF=FG, ∠EFG=90°.
∴BE∥GF.
∴四边形 BEFG 是平行四边形.
又∵∠EFG=90°, EF=FG,
∴四边形 BEFG是正方形.
∴BE=BG, ∠EBG=90°.
∴∠EBG=∠ABC=90°.
∴∠ABE=∠CBG.
又∵AB=BC,
∴△ABE≌△CBG(SAS).
故②正确.
故④正确.
∵正方形ABCD的边长为4,
如图84所示,连接EG.
∵四边形BEFG是正方形,
故③错误.
故答案为①②④.
7. 解: (1) 四边形ABDE是平行四边形.
理由: ∵△ABC≌△DEF ,
∴AB=DE, ∠BAC=∠EDF.
∴AB∥DE.
∴四边形ABDE是平行四边形.
(2) 如图85所示, 连接BE交AD于点O.
∵四边形ABDE为矩形,
∴OA=OD=OB=OE.
设AF = xcm, 则
∵在Rt△OFE中,
即
(3) BD=2OF.
理由:如图86所示,延长OF 交AE于点H.
∵由矩形的性质及旋转的性质知, OA=OB=OE=OD,
∴∠OAB=∠OBA=∠ODE=∠OED, ∠OBD=∠ODB, ∠OAE=∠OEA.
∴∠BDE+∠DEA=∠ABD+∠EAB.
∵∠ABD+∠BDE+∠DEA+∠EAB=360°,
∴∠ABD+∠EAB=180°.
∴AE∥BD.
∴∠OHE=∠ODB .
∵EF平分∠AEO,
∴∠OEF =∠HEF.
∵∠EFO=∠EFH=90°, EF=EF,
∴△EFO≌△EFH(ASA).
∴EO=EH, FO=FH.
∴∠EHO=∠EOH =∠OBD=∠ODB.
∴△EOH≌△OBD(AAS).
∴BD=OH=2OF.
8. 解: (1) ∵矩形ABCG与矩形CDEF全等,
∴AC=CE, ∠ACB=∠ECF .
∵∠ACB+∠ACG=90°,
∴∠ACE=90°.
(2) ∵AC=CE, CF平分∠ACE,
∴由等腰三角形“三线合一”得, CF⊥AE, AF=EF=4.
设点E到直线AC的距离为d.
∴此时点E到直线AC 的距离为
(3)如图87所示,过点E作AG的平行线交DM 的延长线于点H,连接EG.
∵HE∥AG,
∴∠H=∠MGA.
∵CG=CD,
∴∠CGD=∠CDG.
∵∠AGC=∠CDE=90°,
∴∠MGA+∠CGD=90°, ∠CDG+∠HDE=90°.
∴∠MGA=∠HDE.
∴∠HDE=∠H .
∴HE =ED=AG.
在△HME与△GMA中,
∴△HME≌△GMA(AAS).
∴AM=ME.
∵AG的中点为点N,
∵ 在矩形 CDEF 绕 点 C 逆时 针旋转 的过程中 , GE 的 范围为
∴GE的最小值为
∴MN的最小值为
