人教版八年级数学下册第18章 平行四边形18.2.2菱形 同步培优(含解析)
文档属性
| 名称 | 人教版八年级数学下册第18章 平行四边形18.2.2菱形 同步培优(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 509.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:38:00 | ||
图片预览




文档简介
18.2.2菱形
一、知识梳理
1.定义
一组邻边相等的平行四边形是菱形.
如图2-1所示, 在 ABCD中, 若AB=BC, 则四边形ABCD是菱形.
2.性质
如图2-2所示, 在菱形ABCD中,
(1)边: 对边平行且四边相等,即AB∥CD,AD∥BC,且AB=BC=CD=AD;
(2)角:对角相等,邻角互补,即∠BAD=∠BCD,∠ABC=∠ADC,∠ABC+∠BCD=180°;
(3)对角线:对角线互相垂直平分,且每一条对角线平分每一组对角,即OA=OC,OB=OD,AC⊥BD,∠BAO=∠DAO=∠BCO=∠DCO,∠ADO=∠CDO=∠ABO=∠CBO;
(4)对称性:中心对称图形,对称中心是对角线的交点,即点O;轴对称图形,对称轴有两条,是两条对角线所在的直线.
3.重要结论
(1)菱形的面积等于底乘高,也等于对角线乘积的一半,即 如图2-3所示.
(2)含60° (或120°)的菱形,连接短对角线,得到两个全等的等边三角形;连接长对角线,得到两个全等的等腰三角形.
如图2-4所示, 在菱形ABCD中, 若. 则 和 均为等边三角形,△ABD和△BCD均为顶角为120°的等腰三角形,AB∶AD∶BD=
注意:见到含60° (或120°)的菱形,连接对角线.
4.判定
如图2-5所示,四边形ABCD 满足下列任意情况时,可判定为菱形.
(1)一组邻边相等的平行四边形是菱形(定义).
∵四边形ABCD 是平行四边形, AB=BC,
∴四边形ABCD是菱形.
(2)对角线互相垂直的平行四边形是菱形.
∵四边形ABCD 是平行四边形, AC⊥BD,
∴四边形ABCD是菱形.
(3)四条边都相等的四边形是菱形.
∵AB=BC=CD=AD,
∴四边形ABCD 是菱形.
二、分层练习
万丈高楼平地起
1.菱形具有但一般平行四边形不具有的性质是 ( ).
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等
2. 如图2-6所示, 菱形ABCD的对角线AC, BD 相交于点O, 点E为CD的中点. 若OE=2, 则菱形的周长为 ( ).
A. 10
B. 12
C. 16
D. 20
3. 如图2-7 所示, 四边形ABCD 是菱形, AC=24, BD=10, 则菱形ABCD的边长是 ( ).
A. 13
B. 12
C. 26
D. 52
4. 菱形 ABCD 如图2-8 所示, 对角线 AC, BD 相交于点 O. 若 菱形ABCD的面积为24,且点E为AD的中点,则线段OE的长为( ).
A. 2
B. 2.5
C. 4
D. 5
5. 如图2-9 所示, 四边形 ABCD 为菱形, 对角线 AC, BD 相交于点 O,DH⊥AB 于点 H, 连接OH, ∠CAD=25°, 则∠DHO的度数是 ( ).
A. 20°
B. 25°
C. 30°
D. 35°
6.如图2-10所示,在菱形ABCD中,点M,N分别在AB,CD上,且. MN与AC相交于点O,连接BO.若∠DAC=35°,则∠OBC的大小为 度.
7. 如图2-11 所示, 在菱形ABCD中, AB=5, BD=8, 过点D作 交BA 的延长线于点 E,则线段DE的长为 ( ).
A. 4
B. 3
8. 如图2-12所示, 若菱形ABCD中, AE垂直平分BC于点E, 则BC的长是 ( ).
A. 1cm
C. 3cm
D. 4cm
9. 如图2-13 所示, 在菱形ABCD中, 于点E,交对角线AC于点 P,过点P作PF⊥CD于点 F.若 的周长为8,则菱形ABCD的面积为( ).
A. 16
C. 32
10. 如图2-14 所示, 在 ABCD中, 对角线AC和BD相交于点O, 添加下列条件不能判定四边形ABCD是菱形的是( ).
A. AB=BC
B. AC⊥BD
C. AC平分∠DAB
D. AC=BD
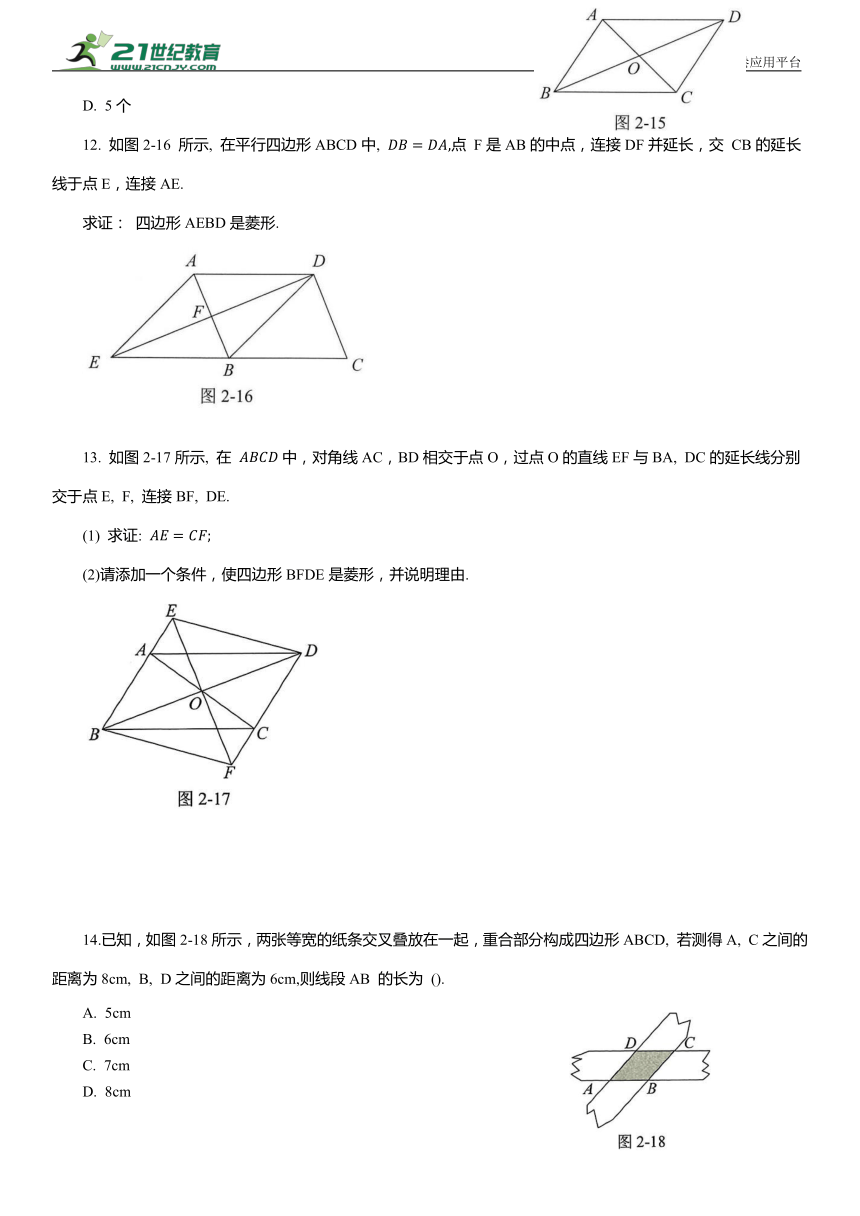
11.如图2-15所示,已知四边形ABCD是平行四边形,对角线AC,BD相交于点 O, 给出下列条件: ①AB=AD; ②AC=BD; ③∠BOC=90°;④∠ABC=∠BCD; ⑤∠ADB=∠CDB. 其中, 能判定四边形 ABCD 是菱形的条件有 ( ).
A. 2个
B. 3个
C. 4个
D. 5个
12. 如图2-16 所示, 在平行四边形ABCD中, 点 F是AB的中点,连接DF并延长,交 CB的延长线于点E,连接AE.
求证: 四边形AEBD是菱形.
13. 如图2-17所示, 在 中,对角线AC,BD相交于点O,过点O的直线EF与BA, DC的延长线分别交于点E, F, 连接BF, DE.
(1) 求证:
(2)请添加一个条件,使四边形BFDE是菱形,并说明理由.
14.已知,如图2-18所示,两张等宽的纸条交叉叠放在一起,重合部分构成四边形ABCD, 若测得A, C之间的距离为8cm, B, D之间的距离为6cm,则线段AB 的长为 ().
A. 5cm
B. 6cm
C. 7cm
D. 8cm
15.如图2-19所示,在平行四边形ABCD中,对角线AC的垂直平分线分别与AD, AC, BC相交于点 E, O, F. 下列结论正确的个数有 ( ).
① 四边形AFCE 为菱形;
② △ABF≌△CDE;
③ 当点F为BC中点时, ∠ACD=90°.
A. 0个 B. 1个 C. 2个 D. 3个
16. 如图2-20 所示, 在四边形ABCD中, AD∥BC, 对角线 BD 的垂直平分线与边AD, BC分别相交于点 M, N.
(1) 求证: 四边形 BNDM是菱形;
(2) 若 BD=12, MN=4, 求菱形BNDM的周长.
17. 如图2-21 所示, 在平行四边形ABCD中, 的角平分线交AD于点 E,过点E作. 交BC于点F.
(1) 求证: 四边形ABFE 是菱形;
(2) 若 求平行四边形ABCD的面积.
18. 如图2-22 所示, 在平行四边形ABCD中, AE平分 交BC于点E ,BF平分 交AD于点F. AE与BF相交于点P,连接EF,PD, PC.
(1) 求证: 四边形ABEF 是菱形;
(2) 若 求 的度数.
19.将三角形纸片 沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图2-23 (a)所示;再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE, DF,如图2-23(b)所示.解决下列问题:
(1) 四边形AEDF 的形状是 ;
(2) 当 时,
20. 如图2-24所示, 在平行四边形ABCD中, 于点E,点F, G分别是AD, BC的中点, 连接CF , EF , FG, 下列四种说法中正确的有 .(填序号)( ②四边形A BGF是 菱形; ③BC=2EG; ④∠DFC=∠EFG.
1.解:由菱形性质可知,其对角相等, 四边相等,对边平行,对角线互相垂直,且每一条对角线平分一组对角.
由平行四边形的性质可知,其对角相等,对边平行且相等,对角线互相平分.故选C.
2. 解: ∵四边形ABCD 是菱形,
∴AB=BC=CD=DA, AC⊥BD.
∴∠COD=90°.
又∵点E 是CD的中点,
∴OE 是Rt△COD 斜边上的中线.
∴CD=2OE=2×2=4.
∴菱形ABCD的周长=4CD
=4×4=16.
故选C.
3. 解: ∵四边形ABCD 是菱形,
∴在 中, 由勾股定理得, 故选A.
4. 解: ∵四边形ABCD 是菱形,
∴AC⊥BD, AO=CO, BO=DO=3.
∵BD=6, 菱形ABCD 的面积为24,
即 解得AC=8.
∴AO=4.
∴在 Rt△AOD中, 由勾股定理得, AD=5.
∵点E为AD的中点, AC⊥BD,
故选B.
5 解: ∵四边形ABCD 是菱形,
∴AD=AB, BO=DO, ∠BAD=2∠CAD=50°.
中小学教育资源及组卷应用平台
∴∠ABD=(180°-∠BAD)÷2=65°.
∵DH⊥AB, BO=DO,
故选B.
6. 解: ∵四边形ABCD 为菱形,
∴AB∥CD, AB=BC.
∴∠MAO=∠NCO,
∠AMO=∠CNO.
在△AMO和△CNO中,
∴△AMO≌△CNO (ASA).
7.解: 如图3所示,设AC与BD的交点为O.
∵四边形ABCD 是菱形, BD=8,
∴AC=2OA=6.
故选D.
8. 解: 连接AC, 如图4所示.
∵四边形ABCD 是菱形,
∴AB=BC.
∵AE 垂直平分BC于点 E,
∴AB=AC, BE=EC, ∠AEB=90°.
∴AB=BC=AC.
是等边三角形.
∵在 中,
解得 (负值已舍去).
故选B.
9. 解: ∵四边形ABCD 是菱形,∴BC=CD, ∠BCD=∠BAD,∠ACB=∠ACD, AD∥BC.
∴∠BAD+∠B=180°.
∵∠DAB=45°,
∴∠BCD=∠BAD=45°.
∵DE⊥BC,
∴△CDE 是等腰直角三角形.
∵PF⊥CD,
∴△DPF 是等腰直角三角形.
设 则
的周长为8,
解得
∴菱形ABCD的面积:
故选D.
10. 解: 当. 或 时,均可判定平行四边形ABCD 是菱形.
∵AC平分∠DAB,
∴∠BAC=∠DAC.
∵四边形ABCD 是平行四边形,
∴AB∥CD.
∴∠BAC=∠DCA.
∴∠DAC=∠DCA.
∴CD=AD.
∴平行四边形ABCD 是菱形.
当AC=BD时,只能判定平行四边形ABCD 是矩形.
故选 D.
11. 解: ①∵四边形ABCD 是平行四边形, AB=AD,
∴平行四边形ABCD 是菱形.
②∵四边形ABCD 是平行四边形,AC=BD,
∴平行四边形ABCD 是矩形.
③∵∠BOC=90°,
∴AC⊥BD.
又∵四边形ABCD 是平行四边形,
∴四边形ABCD是菱形.
④∵四边形ABCD 是平行四边形,
∴AB∥CD.
∴∠ABC+∠BCD=180°.
∴平行四边形ABCD 是矩形.
⑤∵四边形ABCD 是平行四边形,
∴平行四边形ABCD是菱形.
∴能判定四边形ABCD 是菱形的条件有3个.
故选B.
12.证明: ∵四边形ABCD 是平行四边形,
∴AD∥CB.
∴∠DAF=∠EBF.
∵点F是AB的中点,
∴AF=BF.
∵∠AFD=∠BFE,
∴△AFD≌△BFE (ASA).
∴AD=EB.
又∵AD∥EB,
∴四边形AEBD是平行四边形.
又∵DB=DA,
∴平行四边形AEBD 是菱形.
13. (1) 证明: ∵四边形ABCD是平行四边形,
∴OA=OC, AB∥CD.
∵点 E, F分别在 BA, DC的延长线上,
∴∠AEO=∠CFO.
在△AOE和△COF中,
∴△AOE≌△COF(AAS).
∴AE=CF.
(2) 解: 添加的条件为EF⊥BD.
∵四边形ABCD是平行四边形,
∴OB=OD.
∵由 (1) 可知, △AOE≌△COF,
∴OE=OF.
∴四边形BFDE是平行四边形.
∵EF⊥BD,
∴四边形BFDE是菱形.
欲穷千里目,更上一层楼
14. 解: 如图5所示, 连接AC, BD交于点O, 过点A作. 于点R, BC于点S.
∵由题意可知, AD∥BC, AB∥CD,
∴四边形ABCD 是平行四边形.
∵两张纸条等宽, AR⊥CD, AS⊥BC,
∴AR=AS.
∴BC=CD.
∴平行四边形ABCD 是菱形.
∴AC⊥BD.
∵在Rt△AOB 中,
故选A.
15.解:∵四边形ABCD为平行四边形,
∴AD∥BC, AD=BC, AB∥CD,
AB=CD, ∠B=∠D.
∴∠EAC=∠FCA.
∵EF 垂直平分AC,
∴OA=OC, EA=EC.
在△AOE和△COF中,
∴△AOE≌△COF (ASA).
∴OE=OF.
∴四边形AFCE为平行四边形.
∵EF 垂直平分AC,
∴平行四边形AFCE 是菱形,故①正确.
∴AE=CF.
∵BF=BC-FC, DE=AD--AE,
∴BF=DE.
在△ABF和△CDE中,
∴△ABF≌△CDE(SAS),故②正确.
∵四边形AFCE 是菱形,
∴AF=CF.
∵点F为BC的中点,
∴BF=CF.
∴∠BAC=90°.
∵AB∥CD,
∴∠ACD=∠BAC=90°,故③正确.
∴正确的个数有3个.
故选 D.
16. (1) 证明: ∵AD∥BC,
∴∠DMO=∠BNO.
∵MN是对角线BD 的垂直平分线,
∴OB=OD, MN⊥BD.
在△MOD 和△NOB 中,
∴△MOD≌△NOB (AAS).
∴OM=ON.
∵OB=OD,
∴四边形 BNDM 是平行四边形.
∵MN⊥BD,
∴平行四边形 BNDM 是菱形.
(2) 解: ∵四边形 BNDM 是菱形,BD=12, MN=4,
∴MN⊥BD, BN=DN=DM=BM,
∵同理可证
∴四边形ABEF是平行四边形.
∴四边形ABEF是菱形.
∴在 中,
∴菱形 BNDM的周长=4BN
17.(1)证明: ∵四边形ABCD 是平行四边形,
∴AD∥BC.
∵EF∥AB,
∴四边形ABFE 是平行四边形.
∵AD∥BC,
(2)解:如图6所示,连接AF交BE于点M,过点A作 '于点N,
∵由 (1) 可知, 四边形ABFE是菱形, AB=5, BE=8,
∴∠AMB=90°.
∴AF=2AM=6.
∵AN⊥BF,
即 解得
∵BE平分
∴平行四边形ABFE 是菱形.
18.(1)证明:∵四边形ABCD 是平行
四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
(2) 解: ∵由 (1) 可知, 四边形ABEF 是菱形,
∴∠ABP=∠EBP, AB=AF=BE, AE⊥BF, AP=PE.
∴∠APB=90°. ∵∠ABC=60°, AB=6,
∵AD=9, ∴FD=AD-AF=AD-AB=9-6=3.
∵四边形ABCD 是平行四边形,
∴EC=FD=3, ∠ABC+∠BCD=180°.
∴PE=EC.
∴∠ECP=∠EPC.
∵∠ABC=60°, AB=BE,
∴∠BEA=60°, ∠BCD=180°-∠ABC=120°.
∴∠ECP=30°.
∴∠DCP=90°.
19. 解: 折叠过程及结果如图7 (a)、(b) 所示.
(1)∵由第一次折叠可知, AD为∠CAB的角平分线,
∴∠1=∠2.
∵由第二次折叠可知, ∠CAB=∠EDF , AE=ED, AF=FD,
∴∠1=∠3, ∠2=∠4.
∴∠3=∠4.
在△AED与△AFD中,
100
解题方法详解
∴△AED≌△AFD(ASA).
∴AE=AF, DE=DF.
∴AE=AF=DE=DF.
∴四边形AEDF 是菱形.
故答案为菱形.
(2) ∵四边形AEDF 是菱形, ∠BAC =60°,
∴△AEF 是等边三角形, AD⊥EF.
故答案为
20.解: ∵四边形ABCD是平行四边形,
∴AD∥BC, AD=BC.
∵点F,G分别是AD,BC的中点,
∴AF=BG.
∵AF∥BG,
∴四边形ABGF 是平行四边形.
∴AB∥FG.
∵CE⊥AB,
如图8所示,延长EF,交CD延长线于点M.
∵四边形ABCD 是平行四边形,
∴∠A=∠MDF.
∵点F为AD的中点,
在 和 中,
∴△AEF≌△DMF(ASA).
∴FE=FM , ∠AEF=∠M .
∵CE⊥AB,
∴∠AEC=90°.
∴∠ECD=∠AEC=90°.
∵FM=EF,
∴FC=EF=FM .
∴∠DCF =∠M .
∵四边形ABCD是平行四边形,
∴AB=CD, AD∥BC.
∵AF=DF, AD=2AB,
∴DF=DC.
∴∠DCF =∠DFC.
∴∠DFC=∠M.
∵AB∥CD, AB∥FG,
∴FG∥CD.
∴∠EFG=∠M.
∴∠EFG=∠DFC, 故④正确.
故答案为①②③④.
一、知识梳理
1.定义
一组邻边相等的平行四边形是菱形.
如图2-1所示, 在 ABCD中, 若AB=BC, 则四边形ABCD是菱形.
2.性质
如图2-2所示, 在菱形ABCD中,
(1)边: 对边平行且四边相等,即AB∥CD,AD∥BC,且AB=BC=CD=AD;
(2)角:对角相等,邻角互补,即∠BAD=∠BCD,∠ABC=∠ADC,∠ABC+∠BCD=180°;
(3)对角线:对角线互相垂直平分,且每一条对角线平分每一组对角,即OA=OC,OB=OD,AC⊥BD,∠BAO=∠DAO=∠BCO=∠DCO,∠ADO=∠CDO=∠ABO=∠CBO;
(4)对称性:中心对称图形,对称中心是对角线的交点,即点O;轴对称图形,对称轴有两条,是两条对角线所在的直线.
3.重要结论
(1)菱形的面积等于底乘高,也等于对角线乘积的一半,即 如图2-3所示.
(2)含60° (或120°)的菱形,连接短对角线,得到两个全等的等边三角形;连接长对角线,得到两个全等的等腰三角形.
如图2-4所示, 在菱形ABCD中, 若. 则 和 均为等边三角形,△ABD和△BCD均为顶角为120°的等腰三角形,AB∶AD∶BD=
注意:见到含60° (或120°)的菱形,连接对角线.
4.判定
如图2-5所示,四边形ABCD 满足下列任意情况时,可判定为菱形.
(1)一组邻边相等的平行四边形是菱形(定义).
∵四边形ABCD 是平行四边形, AB=BC,
∴四边形ABCD是菱形.
(2)对角线互相垂直的平行四边形是菱形.
∵四边形ABCD 是平行四边形, AC⊥BD,
∴四边形ABCD是菱形.
(3)四条边都相等的四边形是菱形.
∵AB=BC=CD=AD,
∴四边形ABCD 是菱形.
二、分层练习
万丈高楼平地起
1.菱形具有但一般平行四边形不具有的性质是 ( ).
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等
2. 如图2-6所示, 菱形ABCD的对角线AC, BD 相交于点O, 点E为CD的中点. 若OE=2, 则菱形的周长为 ( ).
A. 10
B. 12
C. 16
D. 20
3. 如图2-7 所示, 四边形ABCD 是菱形, AC=24, BD=10, 则菱形ABCD的边长是 ( ).
A. 13
B. 12
C. 26
D. 52
4. 菱形 ABCD 如图2-8 所示, 对角线 AC, BD 相交于点 O. 若 菱形ABCD的面积为24,且点E为AD的中点,则线段OE的长为( ).
A. 2
B. 2.5
C. 4
D. 5
5. 如图2-9 所示, 四边形 ABCD 为菱形, 对角线 AC, BD 相交于点 O,DH⊥AB 于点 H, 连接OH, ∠CAD=25°, 则∠DHO的度数是 ( ).
A. 20°
B. 25°
C. 30°
D. 35°
6.如图2-10所示,在菱形ABCD中,点M,N分别在AB,CD上,且. MN与AC相交于点O,连接BO.若∠DAC=35°,则∠OBC的大小为 度.
7. 如图2-11 所示, 在菱形ABCD中, AB=5, BD=8, 过点D作 交BA 的延长线于点 E,则线段DE的长为 ( ).
A. 4
B. 3
8. 如图2-12所示, 若菱形ABCD中, AE垂直平分BC于点E, 则BC的长是 ( ).
A. 1cm
C. 3cm
D. 4cm
9. 如图2-13 所示, 在菱形ABCD中, 于点E,交对角线AC于点 P,过点P作PF⊥CD于点 F.若 的周长为8,则菱形ABCD的面积为( ).
A. 16
C. 32
10. 如图2-14 所示, 在 ABCD中, 对角线AC和BD相交于点O, 添加下列条件不能判定四边形ABCD是菱形的是( ).
A. AB=BC
B. AC⊥BD
C. AC平分∠DAB
D. AC=BD
11.如图2-15所示,已知四边形ABCD是平行四边形,对角线AC,BD相交于点 O, 给出下列条件: ①AB=AD; ②AC=BD; ③∠BOC=90°;④∠ABC=∠BCD; ⑤∠ADB=∠CDB. 其中, 能判定四边形 ABCD 是菱形的条件有 ( ).
A. 2个
B. 3个
C. 4个
D. 5个
12. 如图2-16 所示, 在平行四边形ABCD中, 点 F是AB的中点,连接DF并延长,交 CB的延长线于点E,连接AE.
求证: 四边形AEBD是菱形.
13. 如图2-17所示, 在 中,对角线AC,BD相交于点O,过点O的直线EF与BA, DC的延长线分别交于点E, F, 连接BF, DE.
(1) 求证:
(2)请添加一个条件,使四边形BFDE是菱形,并说明理由.
14.已知,如图2-18所示,两张等宽的纸条交叉叠放在一起,重合部分构成四边形ABCD, 若测得A, C之间的距离为8cm, B, D之间的距离为6cm,则线段AB 的长为 ().
A. 5cm
B. 6cm
C. 7cm
D. 8cm
15.如图2-19所示,在平行四边形ABCD中,对角线AC的垂直平分线分别与AD, AC, BC相交于点 E, O, F. 下列结论正确的个数有 ( ).
① 四边形AFCE 为菱形;
② △ABF≌△CDE;
③ 当点F为BC中点时, ∠ACD=90°.
A. 0个 B. 1个 C. 2个 D. 3个
16. 如图2-20 所示, 在四边形ABCD中, AD∥BC, 对角线 BD 的垂直平分线与边AD, BC分别相交于点 M, N.
(1) 求证: 四边形 BNDM是菱形;
(2) 若 BD=12, MN=4, 求菱形BNDM的周长.
17. 如图2-21 所示, 在平行四边形ABCD中, 的角平分线交AD于点 E,过点E作. 交BC于点F.
(1) 求证: 四边形ABFE 是菱形;
(2) 若 求平行四边形ABCD的面积.
18. 如图2-22 所示, 在平行四边形ABCD中, AE平分 交BC于点E ,BF平分 交AD于点F. AE与BF相交于点P,连接EF,PD, PC.
(1) 求证: 四边形ABEF 是菱形;
(2) 若 求 的度数.
19.将三角形纸片 沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图2-23 (a)所示;再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE, DF,如图2-23(b)所示.解决下列问题:
(1) 四边形AEDF 的形状是 ;
(2) 当 时,
20. 如图2-24所示, 在平行四边形ABCD中, 于点E,点F, G分别是AD, BC的中点, 连接CF , EF , FG, 下列四种说法中正确的有 .(填序号)( ②四边形A BGF是 菱形; ③BC=2EG; ④∠DFC=∠EFG.
1.解:由菱形性质可知,其对角相等, 四边相等,对边平行,对角线互相垂直,且每一条对角线平分一组对角.
由平行四边形的性质可知,其对角相等,对边平行且相等,对角线互相平分.故选C.
2. 解: ∵四边形ABCD 是菱形,
∴AB=BC=CD=DA, AC⊥BD.
∴∠COD=90°.
又∵点E 是CD的中点,
∴OE 是Rt△COD 斜边上的中线.
∴CD=2OE=2×2=4.
∴菱形ABCD的周长=4CD
=4×4=16.
故选C.
3. 解: ∵四边形ABCD 是菱形,
∴在 中, 由勾股定理得, 故选A.
4. 解: ∵四边形ABCD 是菱形,
∴AC⊥BD, AO=CO, BO=DO=3.
∵BD=6, 菱形ABCD 的面积为24,
即 解得AC=8.
∴AO=4.
∴在 Rt△AOD中, 由勾股定理得, AD=5.
∵点E为AD的中点, AC⊥BD,
故选B.
5 解: ∵四边形ABCD 是菱形,
∴AD=AB, BO=DO, ∠BAD=2∠CAD=50°.
中小学教育资源及组卷应用平台
∴∠ABD=(180°-∠BAD)÷2=65°.
∵DH⊥AB, BO=DO,
故选B.
6. 解: ∵四边形ABCD 为菱形,
∴AB∥CD, AB=BC.
∴∠MAO=∠NCO,
∠AMO=∠CNO.
在△AMO和△CNO中,
∴△AMO≌△CNO (ASA).
7.解: 如图3所示,设AC与BD的交点为O.
∵四边形ABCD 是菱形, BD=8,
∴AC=2OA=6.
故选D.
8. 解: 连接AC, 如图4所示.
∵四边形ABCD 是菱形,
∴AB=BC.
∵AE 垂直平分BC于点 E,
∴AB=AC, BE=EC, ∠AEB=90°.
∴AB=BC=AC.
是等边三角形.
∵在 中,
解得 (负值已舍去).
故选B.
9. 解: ∵四边形ABCD 是菱形,∴BC=CD, ∠BCD=∠BAD,∠ACB=∠ACD, AD∥BC.
∴∠BAD+∠B=180°.
∵∠DAB=45°,
∴∠BCD=∠BAD=45°.
∵DE⊥BC,
∴△CDE 是等腰直角三角形.
∵PF⊥CD,
∴△DPF 是等腰直角三角形.
设 则
的周长为8,
解得
∴菱形ABCD的面积:
故选D.
10. 解: 当. 或 时,均可判定平行四边形ABCD 是菱形.
∵AC平分∠DAB,
∴∠BAC=∠DAC.
∵四边形ABCD 是平行四边形,
∴AB∥CD.
∴∠BAC=∠DCA.
∴∠DAC=∠DCA.
∴CD=AD.
∴平行四边形ABCD 是菱形.
当AC=BD时,只能判定平行四边形ABCD 是矩形.
故选 D.
11. 解: ①∵四边形ABCD 是平行四边形, AB=AD,
∴平行四边形ABCD 是菱形.
②∵四边形ABCD 是平行四边形,AC=BD,
∴平行四边形ABCD 是矩形.
③∵∠BOC=90°,
∴AC⊥BD.
又∵四边形ABCD 是平行四边形,
∴四边形ABCD是菱形.
④∵四边形ABCD 是平行四边形,
∴AB∥CD.
∴∠ABC+∠BCD=180°.
∴平行四边形ABCD 是矩形.
⑤∵四边形ABCD 是平行四边形,
∴平行四边形ABCD是菱形.
∴能判定四边形ABCD 是菱形的条件有3个.
故选B.
12.证明: ∵四边形ABCD 是平行四边形,
∴AD∥CB.
∴∠DAF=∠EBF.
∵点F是AB的中点,
∴AF=BF.
∵∠AFD=∠BFE,
∴△AFD≌△BFE (ASA).
∴AD=EB.
又∵AD∥EB,
∴四边形AEBD是平行四边形.
又∵DB=DA,
∴平行四边形AEBD 是菱形.
13. (1) 证明: ∵四边形ABCD是平行四边形,
∴OA=OC, AB∥CD.
∵点 E, F分别在 BA, DC的延长线上,
∴∠AEO=∠CFO.
在△AOE和△COF中,
∴△AOE≌△COF(AAS).
∴AE=CF.
(2) 解: 添加的条件为EF⊥BD.
∵四边形ABCD是平行四边形,
∴OB=OD.
∵由 (1) 可知, △AOE≌△COF,
∴OE=OF.
∴四边形BFDE是平行四边形.
∵EF⊥BD,
∴四边形BFDE是菱形.
欲穷千里目,更上一层楼
14. 解: 如图5所示, 连接AC, BD交于点O, 过点A作. 于点R, BC于点S.
∵由题意可知, AD∥BC, AB∥CD,
∴四边形ABCD 是平行四边形.
∵两张纸条等宽, AR⊥CD, AS⊥BC,
∴AR=AS.
∴BC=CD.
∴平行四边形ABCD 是菱形.
∴AC⊥BD.
∵在Rt△AOB 中,
故选A.
15.解:∵四边形ABCD为平行四边形,
∴AD∥BC, AD=BC, AB∥CD,
AB=CD, ∠B=∠D.
∴∠EAC=∠FCA.
∵EF 垂直平分AC,
∴OA=OC, EA=EC.
在△AOE和△COF中,
∴△AOE≌△COF (ASA).
∴OE=OF.
∴四边形AFCE为平行四边形.
∵EF 垂直平分AC,
∴平行四边形AFCE 是菱形,故①正确.
∴AE=CF.
∵BF=BC-FC, DE=AD--AE,
∴BF=DE.
在△ABF和△CDE中,
∴△ABF≌△CDE(SAS),故②正确.
∵四边形AFCE 是菱形,
∴AF=CF.
∵点F为BC的中点,
∴BF=CF.
∴∠BAC=90°.
∵AB∥CD,
∴∠ACD=∠BAC=90°,故③正确.
∴正确的个数有3个.
故选 D.
16. (1) 证明: ∵AD∥BC,
∴∠DMO=∠BNO.
∵MN是对角线BD 的垂直平分线,
∴OB=OD, MN⊥BD.
在△MOD 和△NOB 中,
∴△MOD≌△NOB (AAS).
∴OM=ON.
∵OB=OD,
∴四边形 BNDM 是平行四边形.
∵MN⊥BD,
∴平行四边形 BNDM 是菱形.
(2) 解: ∵四边形 BNDM 是菱形,BD=12, MN=4,
∴MN⊥BD, BN=DN=DM=BM,
∵同理可证
∴四边形ABEF是平行四边形.
∴四边形ABEF是菱形.
∴在 中,
∴菱形 BNDM的周长=4BN
17.(1)证明: ∵四边形ABCD 是平行四边形,
∴AD∥BC.
∵EF∥AB,
∴四边形ABFE 是平行四边形.
∵AD∥BC,
(2)解:如图6所示,连接AF交BE于点M,过点A作 '于点N,
∵由 (1) 可知, 四边形ABFE是菱形, AB=5, BE=8,
∴∠AMB=90°.
∴AF=2AM=6.
∵AN⊥BF,
即 解得
∵BE平分
∴平行四边形ABFE 是菱形.
18.(1)证明:∵四边形ABCD 是平行
四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
(2) 解: ∵由 (1) 可知, 四边形ABEF 是菱形,
∴∠ABP=∠EBP, AB=AF=BE, AE⊥BF, AP=PE.
∴∠APB=90°. ∵∠ABC=60°, AB=6,
∵AD=9, ∴FD=AD-AF=AD-AB=9-6=3.
∵四边形ABCD 是平行四边形,
∴EC=FD=3, ∠ABC+∠BCD=180°.
∴PE=EC.
∴∠ECP=∠EPC.
∵∠ABC=60°, AB=BE,
∴∠BEA=60°, ∠BCD=180°-∠ABC=120°.
∴∠ECP=30°.
∴∠DCP=90°.
19. 解: 折叠过程及结果如图7 (a)、(b) 所示.
(1)∵由第一次折叠可知, AD为∠CAB的角平分线,
∴∠1=∠2.
∵由第二次折叠可知, ∠CAB=∠EDF , AE=ED, AF=FD,
∴∠1=∠3, ∠2=∠4.
∴∠3=∠4.
在△AED与△AFD中,
100
解题方法详解
∴△AED≌△AFD(ASA).
∴AE=AF, DE=DF.
∴AE=AF=DE=DF.
∴四边形AEDF 是菱形.
故答案为菱形.
(2) ∵四边形AEDF 是菱形, ∠BAC =60°,
∴△AEF 是等边三角形, AD⊥EF.
故答案为
20.解: ∵四边形ABCD是平行四边形,
∴AD∥BC, AD=BC.
∵点F,G分别是AD,BC的中点,
∴AF=BG.
∵AF∥BG,
∴四边形ABGF 是平行四边形.
∴AB∥FG.
∵CE⊥AB,
如图8所示,延长EF,交CD延长线于点M.
∵四边形ABCD 是平行四边形,
∴∠A=∠MDF.
∵点F为AD的中点,
在 和 中,
∴△AEF≌△DMF(ASA).
∴FE=FM , ∠AEF=∠M .
∵CE⊥AB,
∴∠AEC=90°.
∴∠ECD=∠AEC=90°.
∵FM=EF,
∴FC=EF=FM .
∴∠DCF =∠M .
∵四边形ABCD是平行四边形,
∴AB=CD, AD∥BC.
∵AF=DF, AD=2AB,
∴DF=DC.
∴∠DCF =∠DFC.
∴∠DFC=∠M.
∵AB∥CD, AB∥FG,
∴FG∥CD.
∴∠EFG=∠M.
∴∠EFG=∠DFC, 故④正确.
故答案为①②③④.
