18.2.1矩形 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 18.2.1矩形 同步练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 429.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:39:06 | ||
图片预览




文档简介
18.2.1 矩形
一、知识梳理
1.定义
有一个角是直角的平行四边形是矩形.
如图3-1所示, 在 ABCD中, 若∠ABC=90°, 则四边形ABCD是矩形.
2.性质
在图3-1所示的矩形ABCD中,
(1) 边: 对边平行且相等, 即AB∥CD且. 且
(2)角:四个角都是直角, 即
(3) 对角线: 对角线相等且互相平分, 即AC=BD, OA=OC=OB=OD;
(4)对称性: 中心对称图形,对称中心是对角线的交点, 即点O;轴对称图形,对称轴有两条,是各边的中垂线.
3.重要结论
对角线夹角为60° (或120°)的矩形,对角线互相平分形成的四个三角形中,有两个全等的等边三角形和两个全等的且顶角为120°的等腰三角形,三边之比为1∶1∶
如图3-2所示,在矩形ABCD中,若 则 均为等边三角形, 均为顶角为 的等腰三角形,等腰三角形的三条边之比AO:DO:AD=1∶1∶
4.判定
如图3-3所示,四边形ABCD满足下列任意情况时,可判定为矩形.
(1)有一个角是直角的平行四边形是矩形(定义).
∵四边形ABCD 是平行四边形,
∴四边形ABCD是矩形.
(2)对角线相等的平行四边形是矩形.
∵四边形ABCD 是平行四边形, AC=BD,
∴四边形ABCD 是矩形.
(3)三个角都是直角的四边形是矩形.
∵∠BCD=∠ABC=∠ADC=90°,
∴四边形ABCD 是矩形.
二、分层练习
1.下列关于矩形的说法不正确的是 ( ).
A.对角线平分且相等 B.四个角都是直角
C.有四条对称轴 D.是中心对称图形
2.如图3-4所示,在矩形ABCD中,对角线AC, BD相交于点O.若 BD=4, 则BC的长为 ( ).
A. 4
C. 3
D. 6
3.如图3-5所示,点O为矩形ABCD对角线AC的中点, OP∥AB交BC于点P,连接OD. 若OP=3, AD=8, 则OD的长为 ( ).
A. 3
B. 4
C. 5
D. 6
4.如图3-6所示,在矩形ABCD中,对角线AC, BD相交于点O, OB=2cm, 则矩形ABCD的面积为 ( ).
5. 如图3-7所示, 在矩形ABCD中, 对角线AC, BD相交于点O, AE垂直平分BO. 若 则OD= ( ).
A. 2
B. 3
C. 4
D. 6
6. 如图3-8所示, 在矩形ABCD中,对角线AC, BD相交于点O, 于点E, 则 的大小是 ().
A. 55°
B. 40°
C. 35°
D. 20°
7. 如图 3-9 所示, 在矩形ABCD中, 于点E. 若. 则 的度数为 ( ).
A. 54°
B. 45°
C. 36°
D. 18°
8. 如图 3-10 所示, 在矩形ABCD中, 对角线AC, BD相交于点O. 若AE平分∠BAD交BC于点E, 且BO=BE, 则.
9. 如图 3-11 所示, 在矩形ABCD中, 垂足为点E,∠BAE=30°, 那么△ECD的面积是 ( ).
10. 如图3-12 所示, 在矩形ABCD中, 对角线AC, BD相交于点O,点P是AD上一动点(不与点A, D重合),过点P作AC和BD的垂线,垂足分别为点E, F ,则PE+PF的值是 ( ).
D. 3
11.如图3-13所示,在平行四边形ABCD中,对角线AC与BD相交于点O,添加下列条件不能判定四边形ABCD是矩形的是 ( ).
A. AC⊥BD
B. AB⊥BC
C. AC=BD
D. ∠1=∠2
12. 如图 3-14 所示, 在四边形ABCD中, 对角线AC, BD相交于点O. 在下列各组条件中,不能判定四边形ABCD是矩形的是 ( ).
A. ∠A=∠C, ∠B+∠C=180°, AC⊥BD
B. AO=CO, BO=DO, ∠A=90°
C. ∠A=∠B=90°, AC=BD
D. AB=CD, AD=BC, AC=BD
13.下列对矩形的判定,正确的个数有 ( ).
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(4)有四个角是直角的四边形是矩形;
(5)四个角都相等的四边形是矩形;
(6)对角线相等,且有一个直角的四边形是矩形;
(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(8)对角线相等且互相垂直的四边形是矩形.
A. 3个 B. 4个 C. 5个 D. 6个
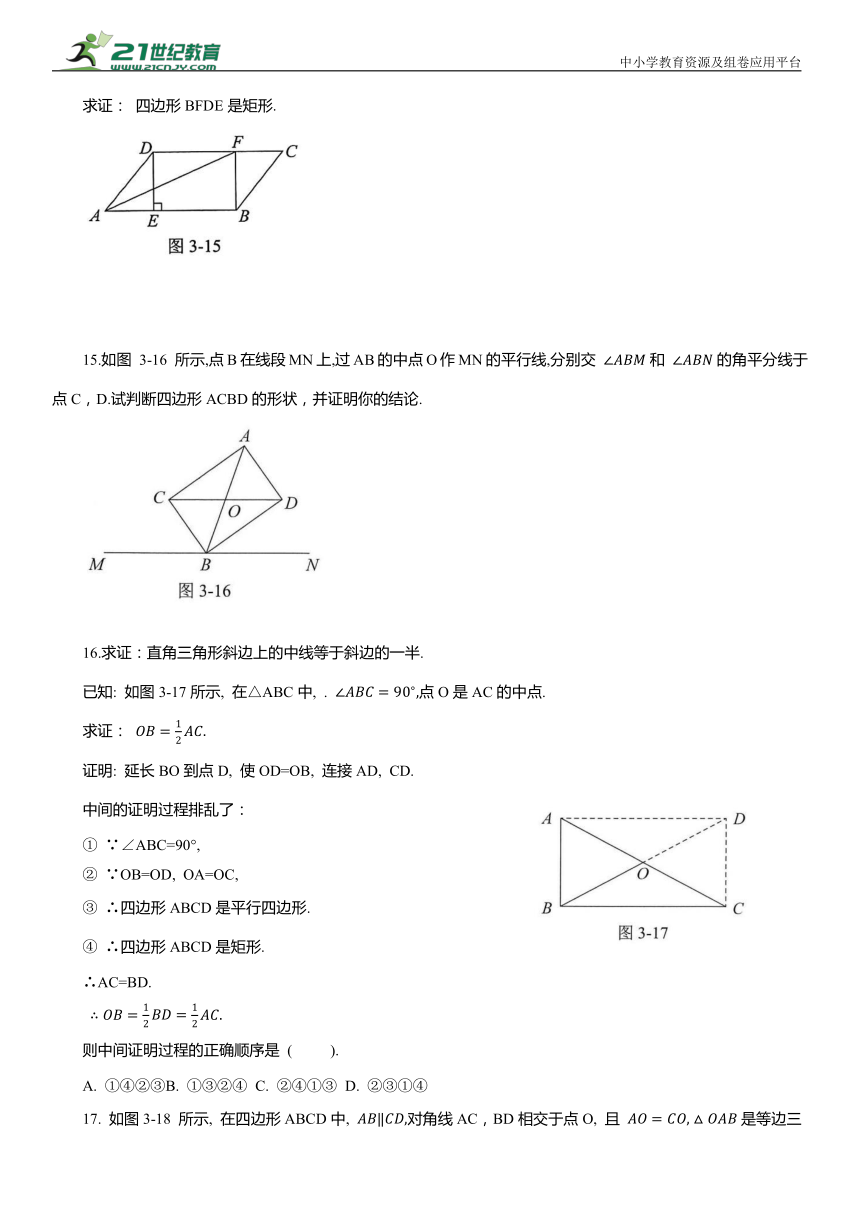
14. 如图3-15 所示, 在平行四边形ABCD中, 过点D作. 于点E,点F在CD上, 连接BF, A F.
求证: 四边形BFDE是矩形.
15.如图 3-16 所示,点B在线段MN上,过AB的中点O作MN的平行线,分别交 和 的角平分线于点C,D.试判断四边形ACBD的形状,并证明你的结论.
16.求证:直角三角形斜边上的中线等于斜边的一半.
已知: 如图3-17所示, 在△ABC中, . 点O是AC的中点.
求证:
证明: 延长BO到点D, 使OD=OB, 连接AD, CD.
中间的证明过程排乱了:
① ∵∠ABC=90°,
② ∵OB=OD, OA=OC,
③ ∴四边形ABCD是平行四边形.
④ ∴四边形ABCD是矩形.
∴AC=BD.
则中间证明过程的正确顺序是 ( ).
A. ①④②③B. ①③②④ C. ②④①③ D. ②③①④
17. 如图3-18 所示, 在四边形ABCD中, 对角线AC,BD相交于点O, 且 是等边三角形.
(1) 求证: 四边形ABCD是矩形;
(2) 若 求BD的长.
18. 如图3-19所示, 在平行四边形ABCD中, 于点E,延长BC至点F, 使 连接AF, DE, DF.
(1) 求证: 四边形AEFD为矩形;
(2) 若 求DF的长.
19. 如图 3-20 所示, 在平行四边形ABCD中, 对角线AC, BD相交于点O,过点A作 于点E,延长BC至点F,使 连接DF.
(1) 求证: 四边形ADFE为矩形;
(2) 连接OF , 若 求OF的 长.
20.如图3-21 所示,点E是平行四边形ABCD对角线AC上的一点,点F 在BE的延长线上,且. EF与CD相交于点G.
(1) 求证:
(2) 若 点G恰好是CD的中点,求证:四边形CFDE是矩形;
(3)在(2)的条件下,若四边形CFDE是正方形,且. 求AB的长.
1.解:矩形的对角线平分且相等,故选项A说法正确.
矩形的四个角都是直角,故选项 B说法正确.
矩形有两条对称轴,故选项C说法不正确.
矩形是中心对称图形,对角线的交点是它的对称中心,故选项D的说法正确.
故选C.
2. 解: ∵四边形ABCD是矩形,
∴OA=OB.
∵∠AOB=60°,
∴△AOB是等边三角形.
∴AB=OB=2.
故选B.
3.解:∵四边形ABCD是矩形, AD=8,OP=3,点O是矩形ABCD对角线AC的中点, OP∥AB,
∴BC=AD=8, ∠B=∠ADC=90°, 点P是BC边的中点.
∴AB=2OP=6.
∵点O为AC的中点, ∠ADC=90°,
故选C.
4. 解: ∵四边形ABCD是矩形,
∴OA=OC=OD=OB.
∴∠OAD=∠ODA.
∵∠AOD=60°,
∴△AOD是等边三角形.
∴OA=OD=AD
=OC=OB=2(cm).
∴AC=4(cm).
故选D.
5. 解: ∵四边形ABCD是矩形,∴OB=OD, OA=OC,AC=BD.
∴OA=OB.
∵AE 垂直平分BO,
∴AB=AO.
∴OA=AB=OB.
∴△BAO是等边三角形.
∴∠AOB=60°.
∴OE=2.
∴OD=OB=2OE=4.
故选C.
6. 解: ∵四边形ABCD是矩形,
∴∠ADC=90°, AC=BD, OA=OC, OB=OD.
∴OC=OD.
∴∠ODC=∠OCD.
∵∠AOD=110°,
∵DE⊥AC,
∴∠ODE=90°-∠DOE=20°.
.
故选C.
7. 解: ∵四边形ABCD是矩形,
∴OA=OB.
∴∠OAB=∠OBA.
∵∠DAE=4∠BAE,
∵AE⊥BD,
∴∠AEB=90°.
故选A.
解: ∵四边形ABCD是矩形,
∴OA=OB.
∵AE 平分.
是等腰直角三角形.
是等边三角形.
故答案为
9. 解: 如图9所示, 过点C作CF⊥BD于点F .
∵在矩形ABCD中, BC=2, AE⊥BD,
∴∠ABE=∠CDF=60°, AB=CD, AD=BC=2, ∠AEB=∠CFD=90°.
∴△ABE≌△CDF (AAS).
∴AE=CF.
∵∠ABE=60°, ∠BAD=90°,
∴∠ADE=30°.
∵AD=2, ∠AED=90°,
∴△ECD 的面积是
故选C.
10. 解: 如图10所示, 连接OP , 过点A作AG⊥BD于点G.
∵在矩形ABCD中, AB=3, AD=4,
即 解得
∵四边形ABCD 是矩形,对角线AC,BC相交于点O,
∴OA=OD.
故选 A.
11.解: ∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,故选项A不能判定四边形ABCD是矩形.
∵AB⊥BC,
∴∠ABC=90°.
∴平行四边形ABCD是矩形,故选项B可以判定四边形ABCD是矩形.
∵四边形ABCD是平行四边形, AC=BD,
∴平行四边形ABCD是矩形,故选项C可以判定四边形ABCD是矩形.
∵四边形ABCD是平行四边形,
∵∠1=∠2,
∴OA=OD.
∴AC=BD.
∴平行四边形ABCD是矩形,故选项D 可以判定四边形ABCD是矩形.故选A.
12. 解: ∵∠B+∠C=180°,
∴AB∥DC.
∵∠A=∠C,
∴∠B+∠A=180°.
∴AD∥BC.
∴四边形ABCD是平行四边形.
又∵AC⊥BD,
∴四边形ABCD是菱形,故选项A不能判定四边形ABCD 是矩形.
∵AO=CO, BO=DO,
∴四边形ABCD是平行四边形.
又∵∠A=90°,
∴四边形ABCD是矩形,故选项B可以判定四边形ABCD 是矩形.
在Rt△ABC和Rt△BAD中,
∴ Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
∴四边形ABCD是平行四边形.
又∵∠A=90°.
∴四边形ABCD是矩形,故选项C可以判定四边形ABCD 是矩形.
∵AB=CD, AD=BC,
∴四边形ABCD是平行四边形.
又∵AC=BD,
∴四边形ABCD是矩形,故选项D可以判定四边形ABCD 是矩形.
故选A.
13.解: ∵对角线相等的平行四边形是矩形,
∴①不正确.
∵对角线互相平分且相等的四边形是矩形,
∴②正确,⑧不正确.
∵有一个角是直角的平行四边形是矩形,
∴③不正确.
∵有三个角是直角的四边形是矩形,
∴④正确.
∵四边形的内角和等于360°,
∴若四个角都相等,则四个角都为直角.
∴四个角都相等的四边形是矩形.
∴⑤正确.
∵对角线相等的平行四边形是矩形,
∴⑥不正确.
∵一组对边平行且相等的四边形是平行四边形,
∴一组邻边垂直,一组对边平行且相等的四边形是矩形.
∴⑦正确.
∴正确的个数有4个.
故选B.
14.证明: ∵四边形ABCD是平行四
边形,
∴AB=DC, AB∥DC.
∴DF∥EB.
∵CF=AE,
∴AB--AE=CD-FC,
即EB=DF.
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°.
∴四边形BFDE是矩形.
15. 解: 四边形ACBD是矩形.
∵CD∥MN,
∴∠OCB=∠CBM.
∵BC平分∠ABM,
∴∠OBC=∠CBM.
∴∠OCB=∠OBC.
∴OC=OB.
∵同理可证, OB=OD.
∴OB=OC=OD.
∵点O是AB的中点,
∴OA=OB.
∴四边形ACBD是平行四边形.
∵CD=OC+OD, AB=OA+OB,
∴AB=CD.
∴四边形ACBD是矩形.
16. 解: 延长BO到点D, 使OD=OB, 连接AD, CD.
∵OB=OD, OA=OC,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形.
∴AC=BD.
∴中间证明过程正确的顺序是②③①④.
故选 D.
17. (1) 证明: ∵AB∥CD,
∴∠OAB=∠OCD.
在△AOB和△COD中,
∴△AOB≌COD(ASA).
∴BO=DO, AB=CD.
∴四边形ABCD是平行四边形.
∵△OAB是等边三角形,
∴OA=OB.
∴OA=OC=OB=OD.
∴AC=BD.
∴平行四边形ABCD是矩形.
(2) 解: ∵△OAB是等边三角形,
∴AB=OA=OB.
∵AO=CO,
∴AC=2OA.
∴AC=2AB.
∵四边形ABCD是矩形,
∴∠ABC=90°.
∴OB=2.
∴BD=2OB=4.
18. (1) 证明: ∵BE=CF,∴BE+CE=CF+CE, 即BC=EF.
∵四边形ABCD是平行四边形,
∴AD=BC=EF.
又∵AD∥EF,
∴四边形AEFD为平行四边形.
中小学教育资源及组卷应用平台
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD为矩形.
(2)解:∵由(1)可知,四边形AEFD为矩形,
∴DF=AE, AF=DE=4.
∵AB=3, DE=4, BF=5,
∴△BAF为直角三角形,∠BAF=90°.
∴ AB·AF=BF·AE,即3×4=5AE, 解得
19. (1) 证明: ∵四边形ABCD是平行
四边形,
∴AB∥DC, AB=DC.
∴∠ABE=∠DCF.
在△ABE和△DCF中,
∴△ABE≌△DCF(SAS).
∴AE=DF,∠DFC=∠AEB=90°.
∴AE∥DF.
∴四边形ADFE 是平行四边形.
∵∠DFC=90°,
∴四边形ADFE是矩形.
(2)解: ∵由(1)可知,四边形ADFE是矩形,
∴EF=AD=3.
∵四边形ABCD是平行四边形,
∴BC=AD=3, CD=AB,OB=OD.
∴BE=CF=BC-EC=1.
∴BF=BC+CF=4.
∵在Rt△ABE中, ∠ABE=60°,
∴∠BAE=90°-∠ABE=30°.
∴AB=2BE=2.
∵∠DFB=90°, OB=OD,
20. (1) 证明: 连接BD, 交AC于点O, 如图11所示.
∵四边形ABCD是平行四边形,
∴BO=DO.
∵BE=EF,
∴OE是△BDF的中位线.
∴OE∥DF, 即DF∥AC.
(2) 证明: 连接DE, CF, 如图12所示.
∵由(1) 可知, DF∥AC,
∵点G是CD的中点,
在 和 中,
∴△DFG≌△CEG(AAS).
∴FG=EG.
∴四边形CFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴AB=CD.
∵2AB=BF,
∴2CD=BF.
又∵EF=BE,
∴CD=EF.
∴四边形CFDE是矩形.
(3) 解: 如图13所示, 设AB=2a, 则BF=4a, BE=EF=CD=2a.
∵四边形ABCD是平行四边形,
∴AD=BC=80, AB∥CD.
∵四边形CFDE是正方形,
∴∠AED=90°, △DEG是等腰直角三角形.
∴AB⊥BF.
∴△ABE是等腰直角三角形.
∴ 在 Rt△ADE 中, 即 解得
a=8,00.
一、知识梳理
1.定义
有一个角是直角的平行四边形是矩形.
如图3-1所示, 在 ABCD中, 若∠ABC=90°, 则四边形ABCD是矩形.
2.性质
在图3-1所示的矩形ABCD中,
(1) 边: 对边平行且相等, 即AB∥CD且. 且
(2)角:四个角都是直角, 即
(3) 对角线: 对角线相等且互相平分, 即AC=BD, OA=OC=OB=OD;
(4)对称性: 中心对称图形,对称中心是对角线的交点, 即点O;轴对称图形,对称轴有两条,是各边的中垂线.
3.重要结论
对角线夹角为60° (或120°)的矩形,对角线互相平分形成的四个三角形中,有两个全等的等边三角形和两个全等的且顶角为120°的等腰三角形,三边之比为1∶1∶
如图3-2所示,在矩形ABCD中,若 则 均为等边三角形, 均为顶角为 的等腰三角形,等腰三角形的三条边之比AO:DO:AD=1∶1∶
4.判定
如图3-3所示,四边形ABCD满足下列任意情况时,可判定为矩形.
(1)有一个角是直角的平行四边形是矩形(定义).
∵四边形ABCD 是平行四边形,
∴四边形ABCD是矩形.
(2)对角线相等的平行四边形是矩形.
∵四边形ABCD 是平行四边形, AC=BD,
∴四边形ABCD 是矩形.
(3)三个角都是直角的四边形是矩形.
∵∠BCD=∠ABC=∠ADC=90°,
∴四边形ABCD 是矩形.
二、分层练习
1.下列关于矩形的说法不正确的是 ( ).
A.对角线平分且相等 B.四个角都是直角
C.有四条对称轴 D.是中心对称图形
2.如图3-4所示,在矩形ABCD中,对角线AC, BD相交于点O.若 BD=4, 则BC的长为 ( ).
A. 4
C. 3
D. 6
3.如图3-5所示,点O为矩形ABCD对角线AC的中点, OP∥AB交BC于点P,连接OD. 若OP=3, AD=8, 则OD的长为 ( ).
A. 3
B. 4
C. 5
D. 6
4.如图3-6所示,在矩形ABCD中,对角线AC, BD相交于点O, OB=2cm, 则矩形ABCD的面积为 ( ).
5. 如图3-7所示, 在矩形ABCD中, 对角线AC, BD相交于点O, AE垂直平分BO. 若 则OD= ( ).
A. 2
B. 3
C. 4
D. 6
6. 如图3-8所示, 在矩形ABCD中,对角线AC, BD相交于点O, 于点E, 则 的大小是 ().
A. 55°
B. 40°
C. 35°
D. 20°
7. 如图 3-9 所示, 在矩形ABCD中, 于点E. 若. 则 的度数为 ( ).
A. 54°
B. 45°
C. 36°
D. 18°
8. 如图 3-10 所示, 在矩形ABCD中, 对角线AC, BD相交于点O. 若AE平分∠BAD交BC于点E, 且BO=BE, 则.
9. 如图 3-11 所示, 在矩形ABCD中, 垂足为点E,∠BAE=30°, 那么△ECD的面积是 ( ).
10. 如图3-12 所示, 在矩形ABCD中, 对角线AC, BD相交于点O,点P是AD上一动点(不与点A, D重合),过点P作AC和BD的垂线,垂足分别为点E, F ,则PE+PF的值是 ( ).
D. 3
11.如图3-13所示,在平行四边形ABCD中,对角线AC与BD相交于点O,添加下列条件不能判定四边形ABCD是矩形的是 ( ).
A. AC⊥BD
B. AB⊥BC
C. AC=BD
D. ∠1=∠2
12. 如图 3-14 所示, 在四边形ABCD中, 对角线AC, BD相交于点O. 在下列各组条件中,不能判定四边形ABCD是矩形的是 ( ).
A. ∠A=∠C, ∠B+∠C=180°, AC⊥BD
B. AO=CO, BO=DO, ∠A=90°
C. ∠A=∠B=90°, AC=BD
D. AB=CD, AD=BC, AC=BD
13.下列对矩形的判定,正确的个数有 ( ).
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(4)有四个角是直角的四边形是矩形;
(5)四个角都相等的四边形是矩形;
(6)对角线相等,且有一个直角的四边形是矩形;
(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(8)对角线相等且互相垂直的四边形是矩形.
A. 3个 B. 4个 C. 5个 D. 6个
14. 如图3-15 所示, 在平行四边形ABCD中, 过点D作. 于点E,点F在CD上, 连接BF, A F.
求证: 四边形BFDE是矩形.
15.如图 3-16 所示,点B在线段MN上,过AB的中点O作MN的平行线,分别交 和 的角平分线于点C,D.试判断四边形ACBD的形状,并证明你的结论.
16.求证:直角三角形斜边上的中线等于斜边的一半.
已知: 如图3-17所示, 在△ABC中, . 点O是AC的中点.
求证:
证明: 延长BO到点D, 使OD=OB, 连接AD, CD.
中间的证明过程排乱了:
① ∵∠ABC=90°,
② ∵OB=OD, OA=OC,
③ ∴四边形ABCD是平行四边形.
④ ∴四边形ABCD是矩形.
∴AC=BD.
则中间证明过程的正确顺序是 ( ).
A. ①④②③B. ①③②④ C. ②④①③ D. ②③①④
17. 如图3-18 所示, 在四边形ABCD中, 对角线AC,BD相交于点O, 且 是等边三角形.
(1) 求证: 四边形ABCD是矩形;
(2) 若 求BD的长.
18. 如图3-19所示, 在平行四边形ABCD中, 于点E,延长BC至点F, 使 连接AF, DE, DF.
(1) 求证: 四边形AEFD为矩形;
(2) 若 求DF的长.
19. 如图 3-20 所示, 在平行四边形ABCD中, 对角线AC, BD相交于点O,过点A作 于点E,延长BC至点F,使 连接DF.
(1) 求证: 四边形ADFE为矩形;
(2) 连接OF , 若 求OF的 长.
20.如图3-21 所示,点E是平行四边形ABCD对角线AC上的一点,点F 在BE的延长线上,且. EF与CD相交于点G.
(1) 求证:
(2) 若 点G恰好是CD的中点,求证:四边形CFDE是矩形;
(3)在(2)的条件下,若四边形CFDE是正方形,且. 求AB的长.
1.解:矩形的对角线平分且相等,故选项A说法正确.
矩形的四个角都是直角,故选项 B说法正确.
矩形有两条对称轴,故选项C说法不正确.
矩形是中心对称图形,对角线的交点是它的对称中心,故选项D的说法正确.
故选C.
2. 解: ∵四边形ABCD是矩形,
∴OA=OB.
∵∠AOB=60°,
∴△AOB是等边三角形.
∴AB=OB=2.
故选B.
3.解:∵四边形ABCD是矩形, AD=8,OP=3,点O是矩形ABCD对角线AC的中点, OP∥AB,
∴BC=AD=8, ∠B=∠ADC=90°, 点P是BC边的中点.
∴AB=2OP=6.
∵点O为AC的中点, ∠ADC=90°,
故选C.
4. 解: ∵四边形ABCD是矩形,
∴OA=OC=OD=OB.
∴∠OAD=∠ODA.
∵∠AOD=60°,
∴△AOD是等边三角形.
∴OA=OD=AD
=OC=OB=2(cm).
∴AC=4(cm).
故选D.
5. 解: ∵四边形ABCD是矩形,∴OB=OD, OA=OC,AC=BD.
∴OA=OB.
∵AE 垂直平分BO,
∴AB=AO.
∴OA=AB=OB.
∴△BAO是等边三角形.
∴∠AOB=60°.
∴OE=2.
∴OD=OB=2OE=4.
故选C.
6. 解: ∵四边形ABCD是矩形,
∴∠ADC=90°, AC=BD, OA=OC, OB=OD.
∴OC=OD.
∴∠ODC=∠OCD.
∵∠AOD=110°,
∵DE⊥AC,
∴∠ODE=90°-∠DOE=20°.
.
故选C.
7. 解: ∵四边形ABCD是矩形,
∴OA=OB.
∴∠OAB=∠OBA.
∵∠DAE=4∠BAE,
∵AE⊥BD,
∴∠AEB=90°.
故选A.
解: ∵四边形ABCD是矩形,
∴OA=OB.
∵AE 平分.
是等腰直角三角形.
是等边三角形.
故答案为
9. 解: 如图9所示, 过点C作CF⊥BD于点F .
∵在矩形ABCD中, BC=2, AE⊥BD,
∴∠ABE=∠CDF=60°, AB=CD, AD=BC=2, ∠AEB=∠CFD=90°.
∴△ABE≌△CDF (AAS).
∴AE=CF.
∵∠ABE=60°, ∠BAD=90°,
∴∠ADE=30°.
∵AD=2, ∠AED=90°,
∴△ECD 的面积是
故选C.
10. 解: 如图10所示, 连接OP , 过点A作AG⊥BD于点G.
∵在矩形ABCD中, AB=3, AD=4,
即 解得
∵四边形ABCD 是矩形,对角线AC,BC相交于点O,
∴OA=OD.
故选 A.
11.解: ∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,故选项A不能判定四边形ABCD是矩形.
∵AB⊥BC,
∴∠ABC=90°.
∴平行四边形ABCD是矩形,故选项B可以判定四边形ABCD是矩形.
∵四边形ABCD是平行四边形, AC=BD,
∴平行四边形ABCD是矩形,故选项C可以判定四边形ABCD是矩形.
∵四边形ABCD是平行四边形,
∵∠1=∠2,
∴OA=OD.
∴AC=BD.
∴平行四边形ABCD是矩形,故选项D 可以判定四边形ABCD是矩形.故选A.
12. 解: ∵∠B+∠C=180°,
∴AB∥DC.
∵∠A=∠C,
∴∠B+∠A=180°.
∴AD∥BC.
∴四边形ABCD是平行四边形.
又∵AC⊥BD,
∴四边形ABCD是菱形,故选项A不能判定四边形ABCD 是矩形.
∵AO=CO, BO=DO,
∴四边形ABCD是平行四边形.
又∵∠A=90°,
∴四边形ABCD是矩形,故选项B可以判定四边形ABCD 是矩形.
在Rt△ABC和Rt△BAD中,
∴ Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
∴四边形ABCD是平行四边形.
又∵∠A=90°.
∴四边形ABCD是矩形,故选项C可以判定四边形ABCD 是矩形.
∵AB=CD, AD=BC,
∴四边形ABCD是平行四边形.
又∵AC=BD,
∴四边形ABCD是矩形,故选项D可以判定四边形ABCD 是矩形.
故选A.
13.解: ∵对角线相等的平行四边形是矩形,
∴①不正确.
∵对角线互相平分且相等的四边形是矩形,
∴②正确,⑧不正确.
∵有一个角是直角的平行四边形是矩形,
∴③不正确.
∵有三个角是直角的四边形是矩形,
∴④正确.
∵四边形的内角和等于360°,
∴若四个角都相等,则四个角都为直角.
∴四个角都相等的四边形是矩形.
∴⑤正确.
∵对角线相等的平行四边形是矩形,
∴⑥不正确.
∵一组对边平行且相等的四边形是平行四边形,
∴一组邻边垂直,一组对边平行且相等的四边形是矩形.
∴⑦正确.
∴正确的个数有4个.
故选B.
14.证明: ∵四边形ABCD是平行四
边形,
∴AB=DC, AB∥DC.
∴DF∥EB.
∵CF=AE,
∴AB--AE=CD-FC,
即EB=DF.
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°.
∴四边形BFDE是矩形.
15. 解: 四边形ACBD是矩形.
∵CD∥MN,
∴∠OCB=∠CBM.
∵BC平分∠ABM,
∴∠OBC=∠CBM.
∴∠OCB=∠OBC.
∴OC=OB.
∵同理可证, OB=OD.
∴OB=OC=OD.
∵点O是AB的中点,
∴OA=OB.
∴四边形ACBD是平行四边形.
∵CD=OC+OD, AB=OA+OB,
∴AB=CD.
∴四边形ACBD是矩形.
16. 解: 延长BO到点D, 使OD=OB, 连接AD, CD.
∵OB=OD, OA=OC,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形.
∴AC=BD.
∴中间证明过程正确的顺序是②③①④.
故选 D.
17. (1) 证明: ∵AB∥CD,
∴∠OAB=∠OCD.
在△AOB和△COD中,
∴△AOB≌COD(ASA).
∴BO=DO, AB=CD.
∴四边形ABCD是平行四边形.
∵△OAB是等边三角形,
∴OA=OB.
∴OA=OC=OB=OD.
∴AC=BD.
∴平行四边形ABCD是矩形.
(2) 解: ∵△OAB是等边三角形,
∴AB=OA=OB.
∵AO=CO,
∴AC=2OA.
∴AC=2AB.
∵四边形ABCD是矩形,
∴∠ABC=90°.
∴OB=2.
∴BD=2OB=4.
18. (1) 证明: ∵BE=CF,∴BE+CE=CF+CE, 即BC=EF.
∵四边形ABCD是平行四边形,
∴AD=BC=EF.
又∵AD∥EF,
∴四边形AEFD为平行四边形.
中小学教育资源及组卷应用平台
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD为矩形.
(2)解:∵由(1)可知,四边形AEFD为矩形,
∴DF=AE, AF=DE=4.
∵AB=3, DE=4, BF=5,
∴△BAF为直角三角形,∠BAF=90°.
∴ AB·AF=BF·AE,即3×4=5AE, 解得
19. (1) 证明: ∵四边形ABCD是平行
四边形,
∴AB∥DC, AB=DC.
∴∠ABE=∠DCF.
在△ABE和△DCF中,
∴△ABE≌△DCF(SAS).
∴AE=DF,∠DFC=∠AEB=90°.
∴AE∥DF.
∴四边形ADFE 是平行四边形.
∵∠DFC=90°,
∴四边形ADFE是矩形.
(2)解: ∵由(1)可知,四边形ADFE是矩形,
∴EF=AD=3.
∵四边形ABCD是平行四边形,
∴BC=AD=3, CD=AB,OB=OD.
∴BE=CF=BC-EC=1.
∴BF=BC+CF=4.
∵在Rt△ABE中, ∠ABE=60°,
∴∠BAE=90°-∠ABE=30°.
∴AB=2BE=2.
∵∠DFB=90°, OB=OD,
20. (1) 证明: 连接BD, 交AC于点O, 如图11所示.
∵四边形ABCD是平行四边形,
∴BO=DO.
∵BE=EF,
∴OE是△BDF的中位线.
∴OE∥DF, 即DF∥AC.
(2) 证明: 连接DE, CF, 如图12所示.
∵由(1) 可知, DF∥AC,
∵点G是CD的中点,
在 和 中,
∴△DFG≌△CEG(AAS).
∴FG=EG.
∴四边形CFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴AB=CD.
∵2AB=BF,
∴2CD=BF.
又∵EF=BE,
∴CD=EF.
∴四边形CFDE是矩形.
(3) 解: 如图13所示, 设AB=2a, 则BF=4a, BE=EF=CD=2a.
∵四边形ABCD是平行四边形,
∴AD=BC=80, AB∥CD.
∵四边形CFDE是正方形,
∴∠AED=90°, △DEG是等腰直角三角形.
∴AB⊥BF.
∴△ABE是等腰直角三角形.
∴ 在 Rt△ADE 中, 即 解得
a=8,00.
