18.2.3 正方形 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 18.2.3 正方形 同步练习(含答案)2024-2025学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 360.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览



文档简介
18.2.3 正 方 形
一、知识梳理
1.定义
有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
如图4-1 所示, 在 ABCD中, 若AB=BC且. 则四边形ABCD是正方形.
2.性质
在图4-1所示的正方形ABCD中,
(1)边:对边平行且四边相等,即, , 且
(2)角:四个角都是直角, 即
(3)对角线:对角线互相平分、垂直且相等,每一条对角线平分一组对角,即AC=BD,AC⊥BD,OA=OC=OB=OD,∠BAO=∠DAO=∠BCO=∠DCO=∠ADO=∠CDO=∠ABO=∠CBO=45°;
(4)对称性:中心对称图形,对称中心是对角线的交点,即点O;
轴对称图形,对称轴有四条,是两条对角线所在直线和各边的中垂线.
3.判定
如图4-2所示, 四边形ABCD满足下列任意情况时,可判定为正方形.
(1)有一组邻边相等,并且有一个角是直角的平行四边形是正方形(定义).
∵四边形ABCD是平行四边形, AB=BC且∠ABC=90°,
∴四边形ABCD是正方形.
(2)有一组邻边相等的矩形是正方形.
∵四边形ABCD 是矩形, AB=BC,
∴四边形ABCD 是正方形.
(3)对角线互相垂直的矩形是正方形.
∵四边形ABCD 是矩形, AC⊥BD,
∴四边形ABCD是正方形.
(4)有一个角是直角的菱形是正方形.
∵四边形ABCD 是菱形, ∠ABC=90°,
∴四边形ABCD是正方形.
(5)对角线相等的菱形是正方形.
∵四边形ABCD 是菱形, AC=BD,
∴四边形ABCD是正方形.
二、分层练习
万丈高楼平地起
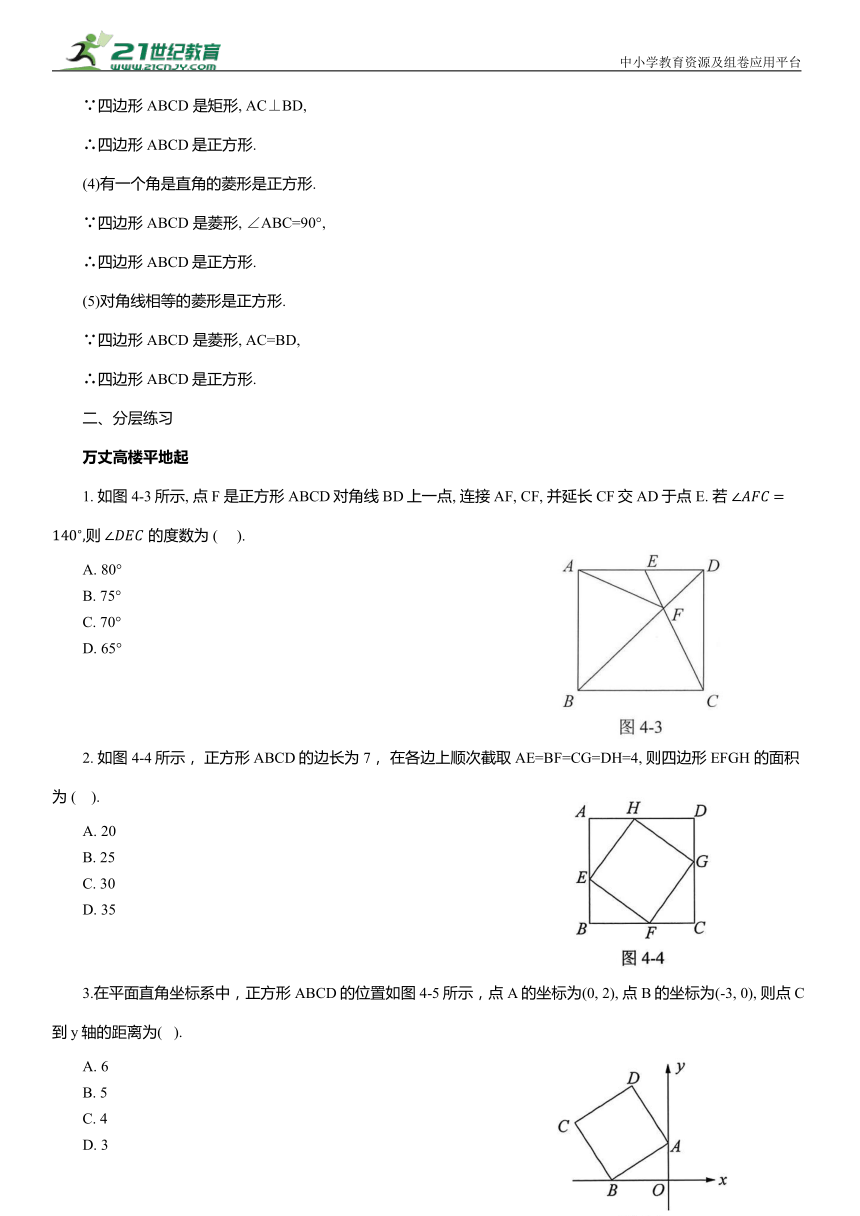
1. 如图4-3所示, 点F 是正方形ABCD对角线BD上一点, 连接AF, CF, 并延长CF交AD于点E. 若 则 的度数为 ( ).
A. 80°
B. 75°
C. 70°
D. 65°
2. 如图 4-4所示, 正方形 ABCD的边长为 7, 在各边上顺次截取AE=BF=CG=DH=4, 则四边形EFGH 的面积为 ( ).
A. 20
B. 25
C. 30
D. 35
3.在平面直角坐标系中,正方形ABCD的位置如图 4-5所示,点A的坐标为(0, 2), 点B的坐标为(-3, 0), 则点C到y轴的距离为( ).
A. 6
B. 5
C. 4
D. 3
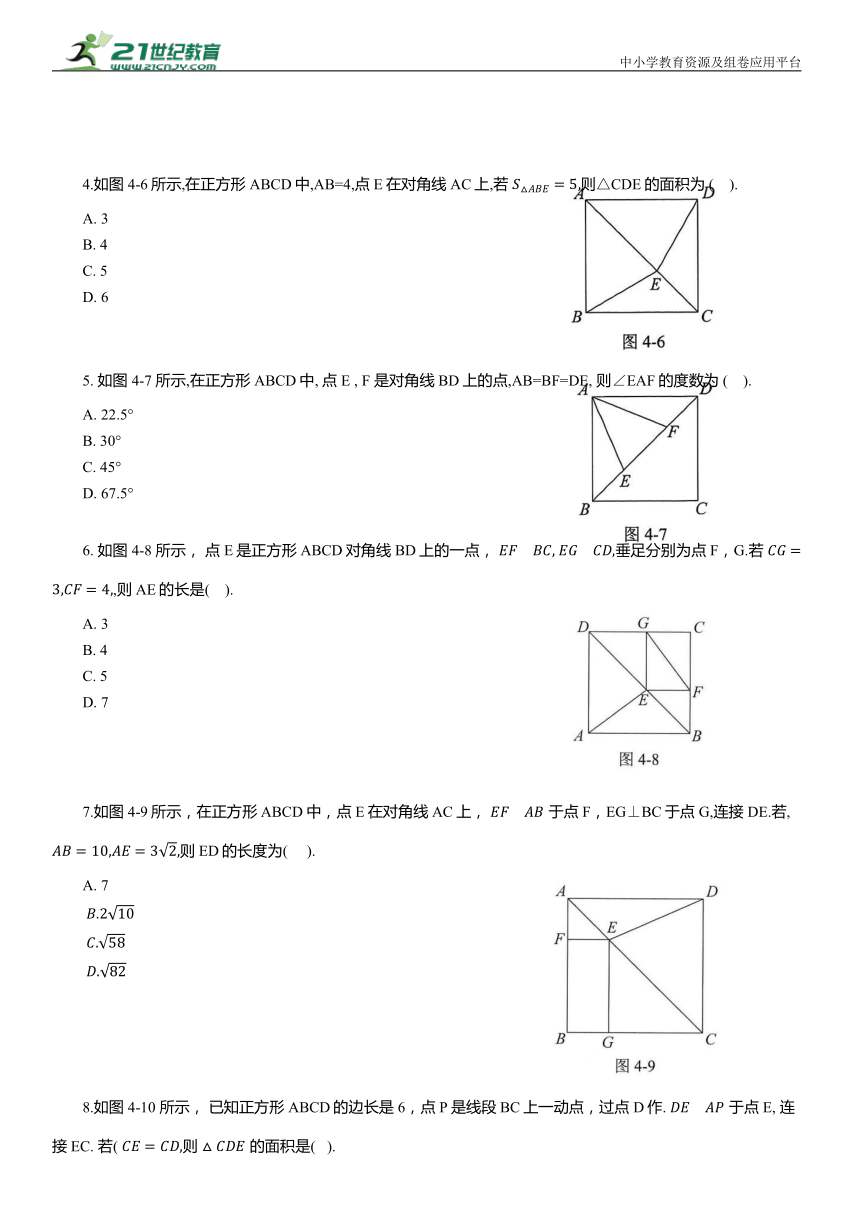
4.如图4-6所示,在正方形ABCD中,AB=4,点E在对角线AC上,若 则△CDE的面积为 ( ).
A. 3
B. 4
C. 5
D. 6
5. 如图 4-7 所示,在正方形ABCD中, 点E , F 是对角线BD上的点,AB=BF=DE, 则∠EAF的度数为 ( ).
A. 22.5°
B. 30°
C. 45°
D. 67.5°
6. 如图 4-8 所示, 点E是正方形ABCD对角线BD上的一点, 垂足分别为点F,G.若 ,则AE的长是( ).
A. 3
B. 4
C. 5
D. 7
7.如图4-9所示,在正方形ABCD中,点E在对角线AC上, 于点F,EG⊥BC于点G,连接DE.若, 则ED的长度为( ).
A. 7
8.如图4-10 所示, 已知正方形ABCD的边长是6,点P是线段BC上一动点,过点D作. 于点E, 连接EC. 若( 则 的面积是( ).
A. 18
C. 14.4
9.如图4-11 所示, 在边长为4的正方形ABCD中,点E, F分别是BC, AB上的点, 连接DE, DF, EF, 满足 若 则EF的长为( ).
A. 2.4
B. 3.4
10.如图4-12所示,已知在正方形ABCD中,对角线AC,BD相交于点O, AE,DF分别是∠OAD与∠ODC的角平分线, AE的延长线与DF相交于点G,则下列结论正确的有 ( ).
①AG⊥DF;
②EF∥AB;
③AB=AF;
④OE:OB=0.5.
A. 1个
B. 2个
C. 3个
D. 4个
11. 在四边形ABCD中, 如果再添加一个条件可判定四边形ABCD 是正方形,那么这个条件可以是 ( ).
12.如图 4-13 所示, 已知四边形ABCD的对角线AC, BD相交于点O,则下列能判定它是正方形的条件是 ( ).
A. AO=BO=CO=DO, AC⊥BD
B. AC=BC=CD=DA
C. AO=CO, BO=DO, AC⊥BD
D. AB=BC, CD⊥DA
13.下列说法正确的有 ().
① 有一组邻边相等的矩形是正方形;
② 对角线互相垂直的矩形是正方形;
③ 有一个角是直角的菱形是正方形;
④ 对角线相等的菱形是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
14. 如图4-14所示,在Rt△ABC中,∠ACB=90°, CD平分∠ACB , DE⊥BC,DF⊥AC, 垂足分别为点E, F.
求证:四边形CFDE是正方形.
15. 如图4-15 所示, 在 中, 过点A的直线. 点E为BC边上一点,过点E作. ,交直线MN于点D,垂足为点F ,连接AE.
(1) 求证:
(2)当点E在BC的中点时,四边形AECD是什么特殊的四边形 说明理由.
(3) 若点E为BC的中点, 当. 满足什么条件时, 四边形AECD是正方形 说明理由.
16. 如图4-16 所示, 边长为4 的菱形ABCD的对角线AC, BD相交于点O,
(1)求证:四边形ABCD是正方形;
(2) 点E是OB上一点, 且 垂足为点H, DH与OC相交于点 F ,求线段OF 的长.
17. 如图 4-17 所示, 点E是正方形ABCD对角线AC上一点, 垂足分别为点F, G .若正方形ABCD的周长是40cm.
(1) 求证: 四边形BFEG是矩形;
(2) 求四边形EFBG的周长;
(3) 当AF 的长为 时, 四边形BFEG是正方形.
18. 如图4-18所示,在 中,两个锐角的角平分线AD,BE相交于点O, 于点F, 于点G.
(1)求证:四边形OGCF是正方形;
(2) 若 求正方形OGCF的边长.
19.如图4-19所示,已知四边形ABCD是正方形, 点E为对角线AC上一动点,连接DE ,过点E作. 交射线BC于点F, 以DE, EF为邻边作矩形DEFG, 连CG.
(1) 求证: 矩形DEFG为正方形;
(2) 求证:
20.如图4-20所示, 已知四边形ABCD为正方形, 点E为对角线AC上一点,连接DE,过点E作. 交BC延长线于点F,以DE,EF为邻边作矩形DEFG,连接CG.下列结论正确的有( ).
①矩形DEFG是正方形;
③CG平分
A. ①③
B. ②④
C. ①②③
D. ①②③④
1. 解: ∵四边形ABCD是正方形,
∴AB=CB,
在△ABF和△CBF中,
∴△ABF≌△CBF(SAS).
∴∠AFB=∠CFB.
∵∠AFC=140°,
∴∠CFB=70°.
∵∠DFC+∠CFB=180°,
∴∠DFC=180°-∠CFB=110°.
∵∠DEF+∠EDF=∠DFC,
∴∠DEC=∠DFC-∠EDF
=110°-45°=65°.
故选 D.
2. 解: ∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA.
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
∴△AEH≌△BFE≌△CGF≌△DHG(SAS).
∴EH=FE=GF=GH,∠AEH =∠BFE.
∴四边形EFGH 是菱形.
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°.
∴∠HEF=90°.
∴四边形 EFGH 是正方形.
∵AB=BC=CD=DA=7,
AE=BF=CG=DH=4,
∴AH=BE=CF=DG=3.
∴EH=FE=GF=HG
∴ 四 边 形 EFGH 的 面 积=5×5=25.
中小学教育资源及组卷应用平台
故选 B.
3.解:过点C作CE⊥x轴于点E,如图14所示,则点C到y轴的距离为OE.
∵点A 的坐标为(0, 2), 点B 的坐标为(-3, 0),
∵CE⊥x轴,
∴∠CEB=90°.
∴∠ECB+∠EBC=90°.
∵四边形ABCD是正方形,
∴BC=AB, ∠CBA=90°.
∴∠EBC+∠ABO=90°.
∴∠ECB=∠ABO.
在△CBE和△BAO中,
∴△CBE≌△BAO(AAS).
∴EB=OA=2.
∴OE=OB+BE=3+2=5.
∴点C到y轴的距离为5.
故选B.
4. 解: 过点E作MN∥AD,交AB于点M, 交CD于点N, 如图15所示.
∵四边形ABCD是正方形,
∴AD⊥AB, AD⊥CD, AB=BC=CD=DA=4.
∵MN∥AD,
∴MN⊥AB, MN⊥CD.
故选 A.
5. 解: ∵四边形ABCD是正方形,
.
∵AB=BF=DE,
∴∠BAF=∠BFA=∠DAE=∠DEA
∴AE=AF.
故选C.
6. 解: 如图16所示, 连接CE.
∵四边形ABCD是正方形,
∴AB=BC, ∠ABD=∠CBD=45°.
在△ABE和△CBE中,
∴△ABE≌△CBE(SAS).
∴AE=CE.
∵EF⊥BC, EG⊥CD, ∠BCD=90°,
∴四边形CFEG是矩形.
∴EF=CG=3, ∠EFC=90°.
∴AE=5.
故选C.
7. 解: 如图17所示, 连接BE.
∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°, AB=AD.
∵AE=AE,
∴△ABE≌△ADE(SAS).
∴BE=DE.
于点F,
故选C.
8. 解: 作CF⊥ED于点F, 如图18所示.
∵四边形ABCD是正方形,
∴AD=DC, ∠CDA=90°.
∴∠ADE+∠FDC=90°.
∵CF⊥DE, CD=CE,
∴∠FDC+∠DCF=90°.
∴∠ADE=∠DCF .
在△ADE和△DCF中,
∴△ADE≌△DCF(AAS).
∴DE=CF.
∵∠CFD=90°, CD=6,
即 解得
故选C.
9. 解: 如图19所示, 在EF上截取EG=EC, 连接DG.
∵四边形ABCD是正方形,
在 和 中,
∴∠DGE=∠C=90°, DG=DC.
∴∠DGF=∠A=90°, DG=DA.
在Rt△DAF和Rt△DGF中,
∴ Rt△DAF≌Rt△DGF(HL).
∴GF=AF=1.
∵EG=EC,
∴BE=BC-EC=4-EG, EF=EG+FG=EG+1, BF=AB-AF=3.
∵在Rt△BEF 中,
解得EG=2.4.
∴EF=EG+FG=2.4+1=3.4.
∴EF的长为3.4.
故选B.
10. 解: ∵四边形ABCD是正方形,
∴∠CAD=∠BDC=45°.
∵AE , DF 分 别 是 ∠OAD 与∠ODC的角平分线,
∴∠DAE=∠CDF.
∵∠ADF+∠CDF=90°,
∴∠DAE+∠ADG=90°.
∴∠AGD=90°, 即 AG⊥DF , 故
故结论②正确.
故结论③正确.
结论①正确.
在△AGF和△AGD中,
∴△AGF≌△AGD(ASA).
∴GF=GD.
∵AG⊥DF,
故结论④错误.
故选 C.
11. 解: ∵在四边形ABCD中, ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
∴AB=CD, ∠D=90°, AC=BD.
故选项A,C,D不能判定四边形ABCD 是正方形.
当BC=CD时,即一组邻边相等时,矩形ABCD为正方形.故选项B可以判定四边形ABCD 是正方形.
故选B.
12. 解: 选项 A 正确, 由AC⊥BD且AC, BD互相平分可判定四边形 ABCD为菱形,再由AC=BD判定为正方形.
选项B错误,不能判定四边形ABCD为正方形.
选项C错误,只能判定四边形ABCD为菱形.
选项D错误,不能判定四边形ABCD为正方形.
故选A.
13.解:一组邻边相等的矩形是正方形,故①正确.
对角线互相垂直的矩形是正方形,故②正确.
对角线相等的菱形是正方形,故③正确.
对角线相等的菱形是正方形,故④正确.
故选D.
14. 证明: ∵∠ACB=90°, DE⊥BC, DF⊥AC,
∴四边形CFDE是矩形.
∵CD平分∠ACB, DE⊥BC, DF⊥AC,
∴DE=DF.
∴四边形CFDE是正方形(有一组邻边相等的矩形是正方形).
15. (1) 证明: ∵DE⊥AC,
∴∠EFC=90°.
∵∠BAC=90°,
∴∠BAC=∠EFC.
∴BE∥AD.
∴四边形ABED 是平行四边形.
∴BE=AD.
(2) 结论: 四边形AECD是菱形.
理由: ∵点E为BC的中点,
∴四边形AECD是平行四边形.
∴四边形AECD是菱形.
(3) 解: 当∠B=45°时, 四边形AECD是正方形.
理由: ∠B=45°, 如图20所示.
∵∠BAC=90°, ∠B=45°,
∴△ABC是等腰直角三角形.
∵点E为BC的中点,
∴AE⊥BC.
∴∠AEC=90°.
∴四边形AECD是正方形.
16. (1) 证明: ∵四边形ABCD是菱形,
∴AD∥BC, ∠BAD=2∠DAC, ∠ABC=2∠DBC.
∴∠BAD+∠ABC=180°.
∵∠CAD=∠DBC,
∴∠BAD=∠ABC.
∴2∠BAD=180°.
∴∠BAD=90°.
∴四边形ABCD是正方形.
(2) 解: ∵四边形ABCD是正方形, .
∴AC⊥BD, AC=BD=4
∴∠COB=∠DOC=90°, CO=DO.
∵DH⊥CE, 垂足为H,
∴∠DHE=90°, ∠EDH+∠DEH=90°.
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH .
在△ECO和△FDO中,
∴△ECO≌△FDO(ASA).
∴OE=OF.
∵BE=1,
17. (1) 证明: ∵四边形ABCD为正方形,
∴AB⊥BC, ∠B=90°.
∵EF⊥AB, EG⊥BC,
∴∠BFE=90°, ∠BGE=90°.
∴四边形BFEG是矩形.
(2) 解: ∵正方形ABCD的周长是40cm,
∴AB=40÷4=10(cm).
∵四边形ABCD为正方形,
∴△AEF 为等腰直角三角形.
∴AF=EF.
∴四边形EFBG的周长=2(EF+BF)=2(AF+BF)=20(cm).
(3) 解: 当AF =5cm时, 四边形BFEG是正方形.
∵AF=5cm, AB=10cm,
∴四边形BFEG是正方形.
故答案为5cm.
18. (1) 证明: 过点O作OH⊥AB于点H, 如图21所示.
∵OF⊥AC于点F , OG⊥BC于点G,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF 是矩形.
∵AD, BE分别是 的角平分线,
∴OG=OH=OF.
∴四边形OGCF 是正方形.
(2) 解: ∵在Rt△ABC中, ∠BAC=60°,
∵AC=4,
∴AB=2AC=2×4=8.
在Rt△AOH和Rt△AOF中,
∴ Rt△AOH≌Rt△AOF(HL).
∴AH=AF.
设正方形OGCF的边长为x,则.
∵ AB=BH+AH,
解得
故正方形OGCF的边长为
19. 证明: (1) 如图22所示, 作EM⊥BC于点M , 于点N.
∵ EM ⊥BC, EN⊥CD, 四边形ABCD为正方形,
∵点E 是正方形ABCD对角线上的点,
在△DEN和△FEM 中,
∴△DEN≌△FEM(ASA).
∴EF=DE.
∴矩形DEFG是正方形.
(2) ∵四边形ABCD和四边形DEFG均为正方形,
∴DE=DG, AD=DC.
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE.
∴△ADE≌△CDG(SAS).
∴AE=CG.
20.解:如图23所示,过点E作EM⊥BC于点M ,过点E作 于点N.
∵四边形ABCD是正方形,
∴∠BCD=90°, ∠ECN=45°.
∵EM⊥BC, EN⊥CD,
∴∠EMC=∠ENC=∠BCD=90°.
∴四边形EMCN 是矩形.
∴∠CEN=∠ECN=45°.
∴NE=NC.
∴四边形EMCN为正方形.
∴EM=EN, ∠DEN+∠NEF=∠MEF+∠NEF=90°.
∴∠DEN=∠MEF.
在△DEN和△FEM中,
∴△DEN≌△FEM(ASA).
∴ED=EF.
∴矩形DEFG为正方形,故①正确.
∴DE=DG, ∠EDC+∠CDG=90°.
∵四边形ABCD是正方形,
∴ AD=DC, ∠ADE+∠EDC=90°.
∴∠ADE=∠CDG.
在△ADE和△CDG中,
∴△ADE≌△CDG(SAS).
∴AE=CG, ∠DCG=∠DAE=45°.
∵∠DCF=90°,
∴CG平分∠DCF, 故③正确.
故②错误.
当DE⊥AC时, 点C 与点F重合, 故④错误.
故选A.
一、知识梳理
1.定义
有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
如图4-1 所示, 在 ABCD中, 若AB=BC且. 则四边形ABCD是正方形.
2.性质
在图4-1所示的正方形ABCD中,
(1)边:对边平行且四边相等,即, , 且
(2)角:四个角都是直角, 即
(3)对角线:对角线互相平分、垂直且相等,每一条对角线平分一组对角,即AC=BD,AC⊥BD,OA=OC=OB=OD,∠BAO=∠DAO=∠BCO=∠DCO=∠ADO=∠CDO=∠ABO=∠CBO=45°;
(4)对称性:中心对称图形,对称中心是对角线的交点,即点O;
轴对称图形,对称轴有四条,是两条对角线所在直线和各边的中垂线.
3.判定
如图4-2所示, 四边形ABCD满足下列任意情况时,可判定为正方形.
(1)有一组邻边相等,并且有一个角是直角的平行四边形是正方形(定义).
∵四边形ABCD是平行四边形, AB=BC且∠ABC=90°,
∴四边形ABCD是正方形.
(2)有一组邻边相等的矩形是正方形.
∵四边形ABCD 是矩形, AB=BC,
∴四边形ABCD 是正方形.
(3)对角线互相垂直的矩形是正方形.
∵四边形ABCD 是矩形, AC⊥BD,
∴四边形ABCD是正方形.
(4)有一个角是直角的菱形是正方形.
∵四边形ABCD 是菱形, ∠ABC=90°,
∴四边形ABCD是正方形.
(5)对角线相等的菱形是正方形.
∵四边形ABCD 是菱形, AC=BD,
∴四边形ABCD是正方形.
二、分层练习
万丈高楼平地起
1. 如图4-3所示, 点F 是正方形ABCD对角线BD上一点, 连接AF, CF, 并延长CF交AD于点E. 若 则 的度数为 ( ).
A. 80°
B. 75°
C. 70°
D. 65°
2. 如图 4-4所示, 正方形 ABCD的边长为 7, 在各边上顺次截取AE=BF=CG=DH=4, 则四边形EFGH 的面积为 ( ).
A. 20
B. 25
C. 30
D. 35
3.在平面直角坐标系中,正方形ABCD的位置如图 4-5所示,点A的坐标为(0, 2), 点B的坐标为(-3, 0), 则点C到y轴的距离为( ).
A. 6
B. 5
C. 4
D. 3
4.如图4-6所示,在正方形ABCD中,AB=4,点E在对角线AC上,若 则△CDE的面积为 ( ).
A. 3
B. 4
C. 5
D. 6
5. 如图 4-7 所示,在正方形ABCD中, 点E , F 是对角线BD上的点,AB=BF=DE, 则∠EAF的度数为 ( ).
A. 22.5°
B. 30°
C. 45°
D. 67.5°
6. 如图 4-8 所示, 点E是正方形ABCD对角线BD上的一点, 垂足分别为点F,G.若 ,则AE的长是( ).
A. 3
B. 4
C. 5
D. 7
7.如图4-9所示,在正方形ABCD中,点E在对角线AC上, 于点F,EG⊥BC于点G,连接DE.若, 则ED的长度为( ).
A. 7
8.如图4-10 所示, 已知正方形ABCD的边长是6,点P是线段BC上一动点,过点D作. 于点E, 连接EC. 若( 则 的面积是( ).
A. 18
C. 14.4
9.如图4-11 所示, 在边长为4的正方形ABCD中,点E, F分别是BC, AB上的点, 连接DE, DF, EF, 满足 若 则EF的长为( ).
A. 2.4
B. 3.4
10.如图4-12所示,已知在正方形ABCD中,对角线AC,BD相交于点O, AE,DF分别是∠OAD与∠ODC的角平分线, AE的延长线与DF相交于点G,则下列结论正确的有 ( ).
①AG⊥DF;
②EF∥AB;
③AB=AF;
④OE:OB=0.5.
A. 1个
B. 2个
C. 3个
D. 4个
11. 在四边形ABCD中, 如果再添加一个条件可判定四边形ABCD 是正方形,那么这个条件可以是 ( ).
12.如图 4-13 所示, 已知四边形ABCD的对角线AC, BD相交于点O,则下列能判定它是正方形的条件是 ( ).
A. AO=BO=CO=DO, AC⊥BD
B. AC=BC=CD=DA
C. AO=CO, BO=DO, AC⊥BD
D. AB=BC, CD⊥DA
13.下列说法正确的有 ().
① 有一组邻边相等的矩形是正方形;
② 对角线互相垂直的矩形是正方形;
③ 有一个角是直角的菱形是正方形;
④ 对角线相等的菱形是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
14. 如图4-14所示,在Rt△ABC中,∠ACB=90°, CD平分∠ACB , DE⊥BC,DF⊥AC, 垂足分别为点E, F.
求证:四边形CFDE是正方形.
15. 如图4-15 所示, 在 中, 过点A的直线. 点E为BC边上一点,过点E作. ,交直线MN于点D,垂足为点F ,连接AE.
(1) 求证:
(2)当点E在BC的中点时,四边形AECD是什么特殊的四边形 说明理由.
(3) 若点E为BC的中点, 当. 满足什么条件时, 四边形AECD是正方形 说明理由.
16. 如图4-16 所示, 边长为4 的菱形ABCD的对角线AC, BD相交于点O,
(1)求证:四边形ABCD是正方形;
(2) 点E是OB上一点, 且 垂足为点H, DH与OC相交于点 F ,求线段OF 的长.
17. 如图 4-17 所示, 点E是正方形ABCD对角线AC上一点, 垂足分别为点F, G .若正方形ABCD的周长是40cm.
(1) 求证: 四边形BFEG是矩形;
(2) 求四边形EFBG的周长;
(3) 当AF 的长为 时, 四边形BFEG是正方形.
18. 如图4-18所示,在 中,两个锐角的角平分线AD,BE相交于点O, 于点F, 于点G.
(1)求证:四边形OGCF是正方形;
(2) 若 求正方形OGCF的边长.
19.如图4-19所示,已知四边形ABCD是正方形, 点E为对角线AC上一动点,连接DE ,过点E作. 交射线BC于点F, 以DE, EF为邻边作矩形DEFG, 连CG.
(1) 求证: 矩形DEFG为正方形;
(2) 求证:
20.如图4-20所示, 已知四边形ABCD为正方形, 点E为对角线AC上一点,连接DE,过点E作. 交BC延长线于点F,以DE,EF为邻边作矩形DEFG,连接CG.下列结论正确的有( ).
①矩形DEFG是正方形;
③CG平分
A. ①③
B. ②④
C. ①②③
D. ①②③④
1. 解: ∵四边形ABCD是正方形,
∴AB=CB,
在△ABF和△CBF中,
∴△ABF≌△CBF(SAS).
∴∠AFB=∠CFB.
∵∠AFC=140°,
∴∠CFB=70°.
∵∠DFC+∠CFB=180°,
∴∠DFC=180°-∠CFB=110°.
∵∠DEF+∠EDF=∠DFC,
∴∠DEC=∠DFC-∠EDF
=110°-45°=65°.
故选 D.
2. 解: ∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA.
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
∴△AEH≌△BFE≌△CGF≌△DHG(SAS).
∴EH=FE=GF=GH,∠AEH =∠BFE.
∴四边形EFGH 是菱形.
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°.
∴∠HEF=90°.
∴四边形 EFGH 是正方形.
∵AB=BC=CD=DA=7,
AE=BF=CG=DH=4,
∴AH=BE=CF=DG=3.
∴EH=FE=GF=HG
∴ 四 边 形 EFGH 的 面 积=5×5=25.
中小学教育资源及组卷应用平台
故选 B.
3.解:过点C作CE⊥x轴于点E,如图14所示,则点C到y轴的距离为OE.
∵点A 的坐标为(0, 2), 点B 的坐标为(-3, 0),
∵CE⊥x轴,
∴∠CEB=90°.
∴∠ECB+∠EBC=90°.
∵四边形ABCD是正方形,
∴BC=AB, ∠CBA=90°.
∴∠EBC+∠ABO=90°.
∴∠ECB=∠ABO.
在△CBE和△BAO中,
∴△CBE≌△BAO(AAS).
∴EB=OA=2.
∴OE=OB+BE=3+2=5.
∴点C到y轴的距离为5.
故选B.
4. 解: 过点E作MN∥AD,交AB于点M, 交CD于点N, 如图15所示.
∵四边形ABCD是正方形,
∴AD⊥AB, AD⊥CD, AB=BC=CD=DA=4.
∵MN∥AD,
∴MN⊥AB, MN⊥CD.
故选 A.
5. 解: ∵四边形ABCD是正方形,
.
∵AB=BF=DE,
∴∠BAF=∠BFA=∠DAE=∠DEA
∴AE=AF.
故选C.
6. 解: 如图16所示, 连接CE.
∵四边形ABCD是正方形,
∴AB=BC, ∠ABD=∠CBD=45°.
在△ABE和△CBE中,
∴△ABE≌△CBE(SAS).
∴AE=CE.
∵EF⊥BC, EG⊥CD, ∠BCD=90°,
∴四边形CFEG是矩形.
∴EF=CG=3, ∠EFC=90°.
∴AE=5.
故选C.
7. 解: 如图17所示, 连接BE.
∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°, AB=AD.
∵AE=AE,
∴△ABE≌△ADE(SAS).
∴BE=DE.
于点F,
故选C.
8. 解: 作CF⊥ED于点F, 如图18所示.
∵四边形ABCD是正方形,
∴AD=DC, ∠CDA=90°.
∴∠ADE+∠FDC=90°.
∵CF⊥DE, CD=CE,
∴∠FDC+∠DCF=90°.
∴∠ADE=∠DCF .
在△ADE和△DCF中,
∴△ADE≌△DCF(AAS).
∴DE=CF.
∵∠CFD=90°, CD=6,
即 解得
故选C.
9. 解: 如图19所示, 在EF上截取EG=EC, 连接DG.
∵四边形ABCD是正方形,
在 和 中,
∴∠DGE=∠C=90°, DG=DC.
∴∠DGF=∠A=90°, DG=DA.
在Rt△DAF和Rt△DGF中,
∴ Rt△DAF≌Rt△DGF(HL).
∴GF=AF=1.
∵EG=EC,
∴BE=BC-EC=4-EG, EF=EG+FG=EG+1, BF=AB-AF=3.
∵在Rt△BEF 中,
解得EG=2.4.
∴EF=EG+FG=2.4+1=3.4.
∴EF的长为3.4.
故选B.
10. 解: ∵四边形ABCD是正方形,
∴∠CAD=∠BDC=45°.
∵AE , DF 分 别 是 ∠OAD 与∠ODC的角平分线,
∴∠DAE=∠CDF.
∵∠ADF+∠CDF=90°,
∴∠DAE+∠ADG=90°.
∴∠AGD=90°, 即 AG⊥DF , 故
故结论②正确.
故结论③正确.
结论①正确.
在△AGF和△AGD中,
∴△AGF≌△AGD(ASA).
∴GF=GD.
∵AG⊥DF,
故结论④错误.
故选 C.
11. 解: ∵在四边形ABCD中, ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
∴AB=CD, ∠D=90°, AC=BD.
故选项A,C,D不能判定四边形ABCD 是正方形.
当BC=CD时,即一组邻边相等时,矩形ABCD为正方形.故选项B可以判定四边形ABCD 是正方形.
故选B.
12. 解: 选项 A 正确, 由AC⊥BD且AC, BD互相平分可判定四边形 ABCD为菱形,再由AC=BD判定为正方形.
选项B错误,不能判定四边形ABCD为正方形.
选项C错误,只能判定四边形ABCD为菱形.
选项D错误,不能判定四边形ABCD为正方形.
故选A.
13.解:一组邻边相等的矩形是正方形,故①正确.
对角线互相垂直的矩形是正方形,故②正确.
对角线相等的菱形是正方形,故③正确.
对角线相等的菱形是正方形,故④正确.
故选D.
14. 证明: ∵∠ACB=90°, DE⊥BC, DF⊥AC,
∴四边形CFDE是矩形.
∵CD平分∠ACB, DE⊥BC, DF⊥AC,
∴DE=DF.
∴四边形CFDE是正方形(有一组邻边相等的矩形是正方形).
15. (1) 证明: ∵DE⊥AC,
∴∠EFC=90°.
∵∠BAC=90°,
∴∠BAC=∠EFC.
∴BE∥AD.
∴四边形ABED 是平行四边形.
∴BE=AD.
(2) 结论: 四边形AECD是菱形.
理由: ∵点E为BC的中点,
∴四边形AECD是平行四边形.
∴四边形AECD是菱形.
(3) 解: 当∠B=45°时, 四边形AECD是正方形.
理由: ∠B=45°, 如图20所示.
∵∠BAC=90°, ∠B=45°,
∴△ABC是等腰直角三角形.
∵点E为BC的中点,
∴AE⊥BC.
∴∠AEC=90°.
∴四边形AECD是正方形.
16. (1) 证明: ∵四边形ABCD是菱形,
∴AD∥BC, ∠BAD=2∠DAC, ∠ABC=2∠DBC.
∴∠BAD+∠ABC=180°.
∵∠CAD=∠DBC,
∴∠BAD=∠ABC.
∴2∠BAD=180°.
∴∠BAD=90°.
∴四边形ABCD是正方形.
(2) 解: ∵四边形ABCD是正方形, .
∴AC⊥BD, AC=BD=4
∴∠COB=∠DOC=90°, CO=DO.
∵DH⊥CE, 垂足为H,
∴∠DHE=90°, ∠EDH+∠DEH=90°.
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH .
在△ECO和△FDO中,
∴△ECO≌△FDO(ASA).
∴OE=OF.
∵BE=1,
17. (1) 证明: ∵四边形ABCD为正方形,
∴AB⊥BC, ∠B=90°.
∵EF⊥AB, EG⊥BC,
∴∠BFE=90°, ∠BGE=90°.
∴四边形BFEG是矩形.
(2) 解: ∵正方形ABCD的周长是40cm,
∴AB=40÷4=10(cm).
∵四边形ABCD为正方形,
∴△AEF 为等腰直角三角形.
∴AF=EF.
∴四边形EFBG的周长=2(EF+BF)=2(AF+BF)=20(cm).
(3) 解: 当AF =5cm时, 四边形BFEG是正方形.
∵AF=5cm, AB=10cm,
∴四边形BFEG是正方形.
故答案为5cm.
18. (1) 证明: 过点O作OH⊥AB于点H, 如图21所示.
∵OF⊥AC于点F , OG⊥BC于点G,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF 是矩形.
∵AD, BE分别是 的角平分线,
∴OG=OH=OF.
∴四边形OGCF 是正方形.
(2) 解: ∵在Rt△ABC中, ∠BAC=60°,
∵AC=4,
∴AB=2AC=2×4=8.
在Rt△AOH和Rt△AOF中,
∴ Rt△AOH≌Rt△AOF(HL).
∴AH=AF.
设正方形OGCF的边长为x,则.
∵ AB=BH+AH,
解得
故正方形OGCF的边长为
19. 证明: (1) 如图22所示, 作EM⊥BC于点M , 于点N.
∵ EM ⊥BC, EN⊥CD, 四边形ABCD为正方形,
∵点E 是正方形ABCD对角线上的点,
在△DEN和△FEM 中,
∴△DEN≌△FEM(ASA).
∴EF=DE.
∴矩形DEFG是正方形.
(2) ∵四边形ABCD和四边形DEFG均为正方形,
∴DE=DG, AD=DC.
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE.
∴△ADE≌△CDG(SAS).
∴AE=CG.
20.解:如图23所示,过点E作EM⊥BC于点M ,过点E作 于点N.
∵四边形ABCD是正方形,
∴∠BCD=90°, ∠ECN=45°.
∵EM⊥BC, EN⊥CD,
∴∠EMC=∠ENC=∠BCD=90°.
∴四边形EMCN 是矩形.
∴∠CEN=∠ECN=45°.
∴NE=NC.
∴四边形EMCN为正方形.
∴EM=EN, ∠DEN+∠NEF=∠MEF+∠NEF=90°.
∴∠DEN=∠MEF.
在△DEN和△FEM中,
∴△DEN≌△FEM(ASA).
∴ED=EF.
∴矩形DEFG为正方形,故①正确.
∴DE=DG, ∠EDC+∠CDG=90°.
∵四边形ABCD是正方形,
∴ AD=DC, ∠ADE+∠EDC=90°.
∴∠ADE=∠CDG.
在△ADE和△CDG中,
∴△ADE≌△CDG(SAS).
∴AE=CG, ∠DCG=∠DAE=45°.
∵∠DCF=90°,
∴CG平分∠DCF, 故③正确.
故②错误.
当DE⊥AC时, 点C 与点F重合, 故④错误.
故选A.
