中点四边形 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 中点四边形 同步练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 376.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:40:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中点四边形
一、知识梳理
1.四边中点的连线
如图6-1所示, 在四边形ABCD中, 点E, F, G, H分别为AB, BC, CD,DA 的中点.
结论: 四边形 EFGH为平行四边形.
证明思路:
∴EH∥GF, EH=GF.
∴四边形EFGH为平行四边形.
注意: 若AC=BD, 易证EH=EF, 则四边形EFGH为菱形.
若AC⊥BD, 易证EH⊥EF, 则四边形EFGH为矩形.
2.对边中点+对角线中点
如图6-2所示, 在四边形ABCD中, 点E, F, G, H分别为AD, BD, BC,AC的中点.
结论: 四边形EFGH为平行四边形.
证明思路:
∴EF∥GH, EF=GH.
∴四边形 EFGH为平行四边形.
注意: 若AB=CD, 易证EF=EH, 则四边形EFGH为菱形.
若AB⊥CD, 易证EF⊥EH, 则四边形EFGH为矩形.
二、分层练习
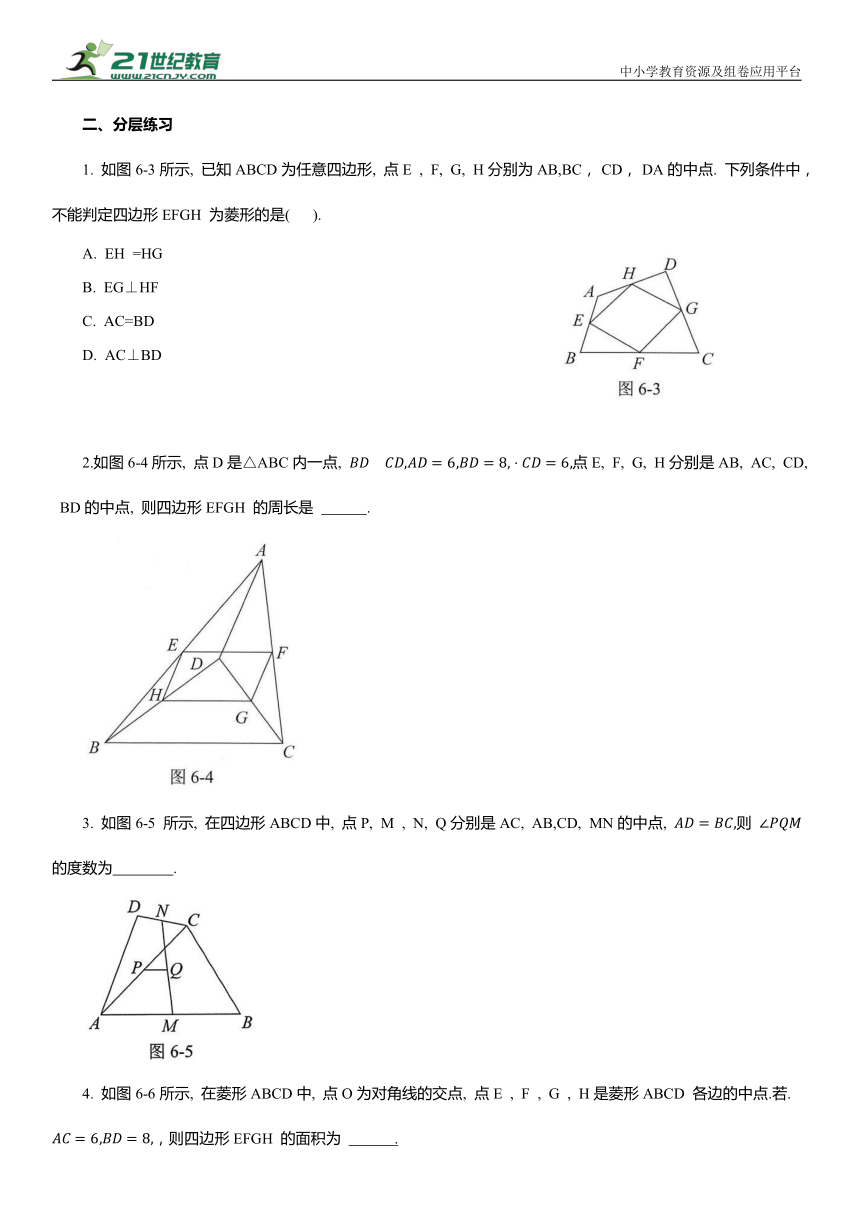
1. 如图6-3所示, 已知ABCD为任意四边形, 点E , F, G, H分别为AB,BC, CD, DA的中点. 下列条件中,不能判定四边形EFGH 为菱形的是( ).
A. EH =HG
B. EG⊥HF
C. AC=BD
D. AC⊥BD
2.如图6-4所示, 点D是△ABC内一点, 点E, F, G, H分别是AB, AC, CD, BD的中点, 则四边形EFGH 的周长是 .
3. 如图6-5 所示, 在四边形ABCD中, 点P, M , N, Q分别是AC, AB,CD, MN的中点, 则 的度数为 .
4. 如图6-6所示, 在菱形ABCD中, 点O为对角线的交点, 点E , F , G , H是菱形ABCD 各边的中点.若. ,则四边形EFGH 的面积为 .
欲穷千里目,更上一层楼
5.某地筹建红军历史博物馆,为了更详尽地再现历史片断,决定把博物馆的平面设计图扩大.如图 6-7所示,已知博物馆原来的平面设计图是平行四边形ABCD,修改后博物馆的平面设计图是四边形EFGH ,其中点A,B ,C, D分别是边EF , FG , GH , HE的中点. 如果博物馆原来的平面设计图ABCD的占地面积为: 则修改后博物馆的平面设计图EFGH的占地面积为 m .
6. 如图6-8所示, 在四边形ABCD中, 点E, F , G , H分别为边AB,BC,CD,DA的中点,连接EG , HF,相交于点O,则 的值为( ).
A. 25
B. 30
C. 35
D. 40
7. 如图6-9所示, 在四边形ABCD中, AB与CD不平行, 点E, F , G , H分别是AD, BD, BC, AC的中点.
(1)求证: 四边形EFGH 是平行四边形;
(2)当AB=CD时,四边形EFGH 是怎样的四边形 证明你的结论.
8.如图6-10所示,两个全等的直角三角形( 和 按照斜边重合的方式摆放, 点E, F, G, H分别为AB, BC, CD, DA的中点.
(1)判断并证明四边形EFGH 的形状;
(2) 若 求四边形EFGH 的面积.
9. 如图6-11 所示, 在四边形ABCD中, AC, BD是对角线, 点E, F , G,H分别是边AB, BC, CD, DA的中点, 依次连接点E, F, G, H.
(1)证明:四边形EFGH 是平行四边形;
(2)在四边形ABCD中,若再补充一个条件: ,则四边形EFGH 是矩形;
(3) 连接EG , FH , 求证:
1. 解: 如图31 所示, 连接AC, BD.
∵点E, F 分别是AB, BC的中点,
∴EF∥AC且
∵同理可证,
∴EF∥HG, EF=HG.
∴四边形EFGH 为平行四边形.
若EH=HG, 则□EFGH为菱形, 故选项A能判定四边形EFGH为菱形.
若EG⊥HF, 则□EFGH 为菱形, 故选项B能判定四边形EFGH为菱形.
∴EH =HG.
∴ □EFGH 为菱形,故选项C能判定四边形EFGH 为菱形.
∵若AC⊥BD, 则EH⊥HG, □EFGH 为矩形, 不一定是菱形,
∴选项 D 不能判定四边形EFGH 为菱形.
故选D.
2. 解: ∵BD⊥CD, BD=8, CD=6,
∵点E, F, G, H分别是AB, AC, CD, BD的中点,
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC.
∴四边形EFGH的周长=6+10=16.
故答案是16.
3. 解: 如图32所示, 连接PM , PN.
∵点P, M 是AC, AB的中点,
∴同理,
∴PM =PN.
∵点Q是MN的中点,
∴PQ⊥MN.
∴∠PQM=90°.
故答案为90°.
4. 解: ∵四边形ABCD是菱形,
∴AC⊥BD.
∵点E, F, G, H分别是边AB, BC, CD和DA的中点,
∴EH∥BD, FG∥BD, EF∥AC, HG∥AC.
∴EH∥FG, EF∥HG.
∴四边形EFGH 是平行四边形.
∵AC⊥BD,
∴∠AOB=90°.
∴∠BAO+∠ABO=90°.
∵∠AEH=∠ABO, ∠BEF=∠EAO,
∴∠AEH+∠BEF=90°.
∴∠HEF=90°.
∴四边形EFGH 是矩形.
∵AC=6, BD=8,
∴四边形EFGH 的面积为=3×4=12.
故答案是12.
5. 解: 如图33 所示, 连接FH, EG, 交于点O, 连接OD, 设CD与FH 交于点M , AD与EG交于点N.
∵点C, D分别是HG, EH 的中点,
∴CD是 的中位线.
∴点M 是OH 的中点.
∴同理可证,
∵同理可证, 四边形EFGH·
∵平行四边形ABCD的面积为
∴四边形EFGH 的面积为(
故答案为600.
6. 解: 如图34所示, 连接EF, FG, GH, HE.
∵点E, F, G, H分别为边AB, BC, CD, DA的中点,
∴EF=FG=GH=HE.
∴四边形EFGH 为菱形.
∴EG⊥FH, OE=OG, OF=OH.
故选 A.
7. (1) 证明: ∵点E, F 分别是AD,BD的中点,
∴EF是. 的中位线.
∴ 同 理 可 证,
∴四边形EFGH 是平行四边形.
(2) 解: 四边形EFGH 是菱形.
∵点G, F分别是BC, BD的中点,
∴FG是 的中位线.
又
∴当 时,
∴平行四边形EFGH 是菱形.
8. 解: (1) 四边形EFGH 为矩形.
理由如下:连接BD,如图35所示.
∵△ABC≌△ADC,
∴AB=AD, CB=CD.
∴AC垂直平分BD.
∵点E, F, G, H分别为AB, BC, CD, DA的中点,
∴EF=HG, EF∥HG.
∴四边形EFGH为平行四边形.
∵EF∥AC, EH∥BD, AC⊥BD,
∴EF⊥EH.
∴∠HEF=90°.
∴四边形EFGH 为矩形.
(2) ∵在Rt△ABC中, ∠BAC=30°,
∴△ABD为等边三角形.
∴四边形EFGH 的面积
会当凌绝顶,一览众山小
9. (1) 证明: ∵点H, G是AD, CD的中点,
∴HG是△ACD的中位线.
∵同理可证,
∴HG∥EF , HG=EF.
∴四边形EFGH 是平行四边形.
(2)解:补充的条件是AC⊥BD,证明如下.
如图36所示,EF与BD相交于点 M.
若AC⊥BD, 则∠DOC=90°.
∵EF∥AC,
∴∠OMF =∠DOC=90°.
∵FG是△BCD的中位线,
∴FG∥BD.
∵由 (1)可知, 四边形EFGH 是平行四边形,
∴四边形EFGH 是矩形.
(3) 证明: 过点H作HP⊥EG于点 P, 过点F作 于点Q,如图37所示.
在Rt△HPE中,
在Rt△HPG中,
∵由 (1)可知,四边形EFGH 是平行四边形,
∴ OP
∴同理可证,
中点四边形
一、知识梳理
1.四边中点的连线
如图6-1所示, 在四边形ABCD中, 点E, F, G, H分别为AB, BC, CD,DA 的中点.
结论: 四边形 EFGH为平行四边形.
证明思路:
∴EH∥GF, EH=GF.
∴四边形EFGH为平行四边形.
注意: 若AC=BD, 易证EH=EF, 则四边形EFGH为菱形.
若AC⊥BD, 易证EH⊥EF, 则四边形EFGH为矩形.
2.对边中点+对角线中点
如图6-2所示, 在四边形ABCD中, 点E, F, G, H分别为AD, BD, BC,AC的中点.
结论: 四边形EFGH为平行四边形.
证明思路:
∴EF∥GH, EF=GH.
∴四边形 EFGH为平行四边形.
注意: 若AB=CD, 易证EF=EH, 则四边形EFGH为菱形.
若AB⊥CD, 易证EF⊥EH, 则四边形EFGH为矩形.
二、分层练习
1. 如图6-3所示, 已知ABCD为任意四边形, 点E , F, G, H分别为AB,BC, CD, DA的中点. 下列条件中,不能判定四边形EFGH 为菱形的是( ).
A. EH =HG
B. EG⊥HF
C. AC=BD
D. AC⊥BD
2.如图6-4所示, 点D是△ABC内一点, 点E, F, G, H分别是AB, AC, CD, BD的中点, 则四边形EFGH 的周长是 .
3. 如图6-5 所示, 在四边形ABCD中, 点P, M , N, Q分别是AC, AB,CD, MN的中点, 则 的度数为 .
4. 如图6-6所示, 在菱形ABCD中, 点O为对角线的交点, 点E , F , G , H是菱形ABCD 各边的中点.若. ,则四边形EFGH 的面积为 .
欲穷千里目,更上一层楼
5.某地筹建红军历史博物馆,为了更详尽地再现历史片断,决定把博物馆的平面设计图扩大.如图 6-7所示,已知博物馆原来的平面设计图是平行四边形ABCD,修改后博物馆的平面设计图是四边形EFGH ,其中点A,B ,C, D分别是边EF , FG , GH , HE的中点. 如果博物馆原来的平面设计图ABCD的占地面积为: 则修改后博物馆的平面设计图EFGH的占地面积为 m .
6. 如图6-8所示, 在四边形ABCD中, 点E, F , G , H分别为边AB,BC,CD,DA的中点,连接EG , HF,相交于点O,则 的值为( ).
A. 25
B. 30
C. 35
D. 40
7. 如图6-9所示, 在四边形ABCD中, AB与CD不平行, 点E, F , G , H分别是AD, BD, BC, AC的中点.
(1)求证: 四边形EFGH 是平行四边形;
(2)当AB=CD时,四边形EFGH 是怎样的四边形 证明你的结论.
8.如图6-10所示,两个全等的直角三角形( 和 按照斜边重合的方式摆放, 点E, F, G, H分别为AB, BC, CD, DA的中点.
(1)判断并证明四边形EFGH 的形状;
(2) 若 求四边形EFGH 的面积.
9. 如图6-11 所示, 在四边形ABCD中, AC, BD是对角线, 点E, F , G,H分别是边AB, BC, CD, DA的中点, 依次连接点E, F, G, H.
(1)证明:四边形EFGH 是平行四边形;
(2)在四边形ABCD中,若再补充一个条件: ,则四边形EFGH 是矩形;
(3) 连接EG , FH , 求证:
1. 解: 如图31 所示, 连接AC, BD.
∵点E, F 分别是AB, BC的中点,
∴EF∥AC且
∵同理可证,
∴EF∥HG, EF=HG.
∴四边形EFGH 为平行四边形.
若EH=HG, 则□EFGH为菱形, 故选项A能判定四边形EFGH为菱形.
若EG⊥HF, 则□EFGH 为菱形, 故选项B能判定四边形EFGH为菱形.
∴EH =HG.
∴ □EFGH 为菱形,故选项C能判定四边形EFGH 为菱形.
∵若AC⊥BD, 则EH⊥HG, □EFGH 为矩形, 不一定是菱形,
∴选项 D 不能判定四边形EFGH 为菱形.
故选D.
2. 解: ∵BD⊥CD, BD=8, CD=6,
∵点E, F, G, H分别是AB, AC, CD, BD的中点,
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC.
∴四边形EFGH的周长=6+10=16.
故答案是16.
3. 解: 如图32所示, 连接PM , PN.
∵点P, M 是AC, AB的中点,
∴同理,
∴PM =PN.
∵点Q是MN的中点,
∴PQ⊥MN.
∴∠PQM=90°.
故答案为90°.
4. 解: ∵四边形ABCD是菱形,
∴AC⊥BD.
∵点E, F, G, H分别是边AB, BC, CD和DA的中点,
∴EH∥BD, FG∥BD, EF∥AC, HG∥AC.
∴EH∥FG, EF∥HG.
∴四边形EFGH 是平行四边形.
∵AC⊥BD,
∴∠AOB=90°.
∴∠BAO+∠ABO=90°.
∵∠AEH=∠ABO, ∠BEF=∠EAO,
∴∠AEH+∠BEF=90°.
∴∠HEF=90°.
∴四边形EFGH 是矩形.
∵AC=6, BD=8,
∴四边形EFGH 的面积为=3×4=12.
故答案是12.
5. 解: 如图33 所示, 连接FH, EG, 交于点O, 连接OD, 设CD与FH 交于点M , AD与EG交于点N.
∵点C, D分别是HG, EH 的中点,
∴CD是 的中位线.
∴点M 是OH 的中点.
∴同理可证,
∵同理可证, 四边形EFGH·
∵平行四边形ABCD的面积为
∴四边形EFGH 的面积为(
故答案为600.
6. 解: 如图34所示, 连接EF, FG, GH, HE.
∵点E, F, G, H分别为边AB, BC, CD, DA的中点,
∴EF=FG=GH=HE.
∴四边形EFGH 为菱形.
∴EG⊥FH, OE=OG, OF=OH.
故选 A.
7. (1) 证明: ∵点E, F 分别是AD,BD的中点,
∴EF是. 的中位线.
∴ 同 理 可 证,
∴四边形EFGH 是平行四边形.
(2) 解: 四边形EFGH 是菱形.
∵点G, F分别是BC, BD的中点,
∴FG是 的中位线.
又
∴当 时,
∴平行四边形EFGH 是菱形.
8. 解: (1) 四边形EFGH 为矩形.
理由如下:连接BD,如图35所示.
∵△ABC≌△ADC,
∴AB=AD, CB=CD.
∴AC垂直平分BD.
∵点E, F, G, H分别为AB, BC, CD, DA的中点,
∴EF=HG, EF∥HG.
∴四边形EFGH为平行四边形.
∵EF∥AC, EH∥BD, AC⊥BD,
∴EF⊥EH.
∴∠HEF=90°.
∴四边形EFGH 为矩形.
(2) ∵在Rt△ABC中, ∠BAC=30°,
∴△ABD为等边三角形.
∴四边形EFGH 的面积
会当凌绝顶,一览众山小
9. (1) 证明: ∵点H, G是AD, CD的中点,
∴HG是△ACD的中位线.
∵同理可证,
∴HG∥EF , HG=EF.
∴四边形EFGH 是平行四边形.
(2)解:补充的条件是AC⊥BD,证明如下.
如图36所示,EF与BD相交于点 M.
若AC⊥BD, 则∠DOC=90°.
∵EF∥AC,
∴∠OMF =∠DOC=90°.
∵FG是△BCD的中位线,
∴FG∥BD.
∵由 (1)可知, 四边形EFGH 是平行四边形,
∴四边形EFGH 是矩形.
(3) 证明: 过点H作HP⊥EG于点 P, 过点F作 于点Q,如图37所示.
在Rt△HPE中,
在Rt△HPG中,
∵由 (1)可知,四边形EFGH 是平行四边形,
∴ OP
∴同理可证,
