新定义四边形 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 新定义四边形 同步练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 440.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:51:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第7节 新定义四边形
一、知识梳理
深刻理解新定义四边形的性质,围绕性质完成题目要求.
二、分层练习
1.定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为“勾股四边形”.
(1)在你学过的特殊四边形中,写出两种“勾股四边形”的名称;
(2) 如图 7-1 所示, 将 绕顶点B 按顺时针方向旋转( 得到 连接AD,DC , CE, 已知
① 求证: 是等边三角形;
② 求证: 即四边形ABCD是“勾股四边形”.
2. 如图 7-2(a) 所示, 在四边形ABCD中, 若∠A, ∠C均为直角, 则称这样的四边形为“美妙四边形”.
(1)在“平行四边形、矩形、菱形”中, 一定是“美妙四边形”.(填写图形名称)
(2) 试证明:
(3) 如图7-2(b) 所示, 在等腰直角三角形ABC中, 点D为BC的中点, 点E, F分别在AB, AC 上, 连接DE, DF, 如果四边形AEDF 是“美妙四边形”,试证明:
3.我们定义对角线互相垂直的四边形叫作“垂美四边形”.
如图 7-3 所示, 点E 是四边形ABCD内一点, 已知 ,对角线AC 与BD相交于O点,BD与EC相交于点F,AC与ED相交于点G .
(1)求证: 四边形ABCD是“垂美四边形”.
(2)猜想四边形ABCD两组对边AB,CD与BC,AD之间的数量关系并说明理由.
(3) 若. , 则CD的长为 .
4.定义:有一组邻边相等的凸四边形叫作“等邻边四边形”.
【概念理解】
(1)下列四边形中是“等邻边四边形”的是 .
A. 矩形 B. 菱形 C.平行四边形 D. 梯形
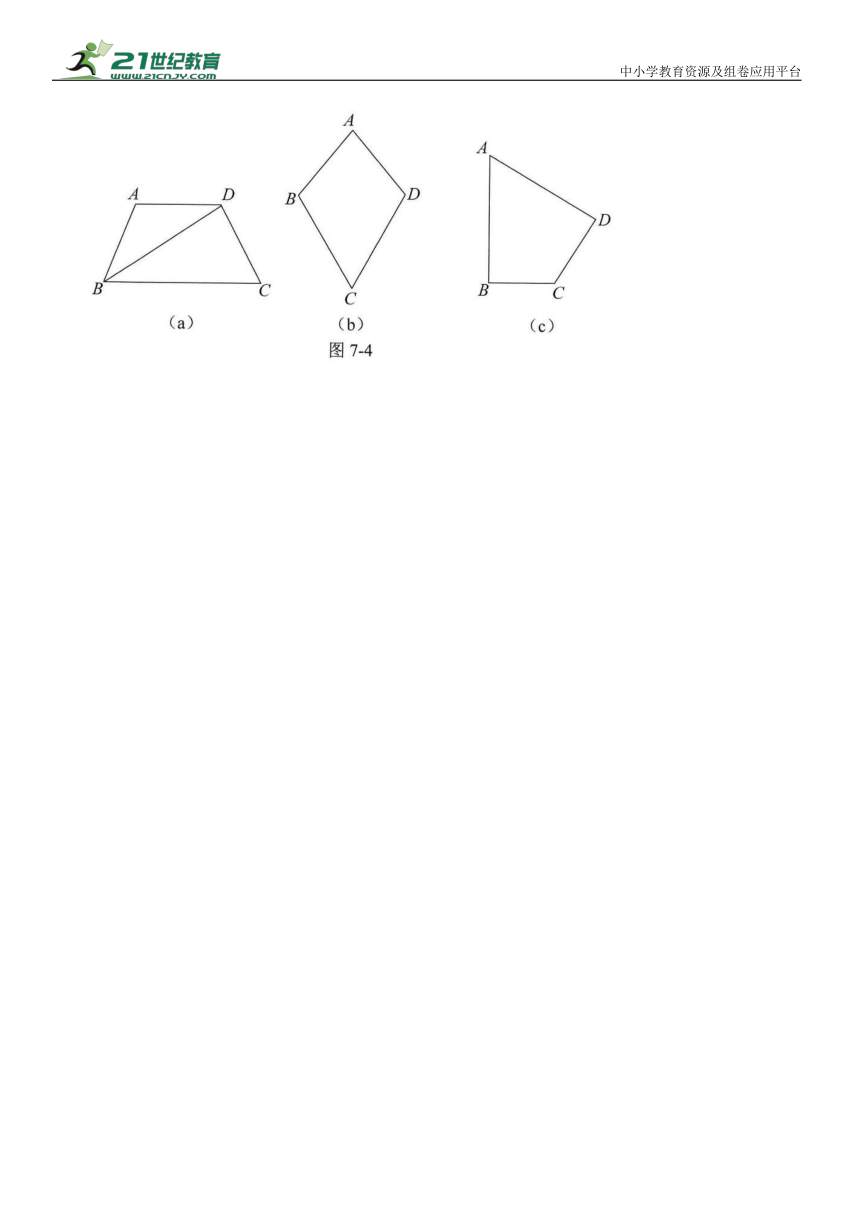
(2)如图7-4(a)所示, 在四边形ABCD中, 若∠ABC=∠BCD, BC∥AD,对角线BD平分∠ABC, 则四边形ABCD “等邻边四边形”. (填“是”或“不是”)
【性质探究】
(1)小红画了一个“等邻边四边形” ABCD,如图7-4(b)所示,其中AB=AD,BC=CD. 若∠A=80°, ∠C=60°, 求出∠B, ∠D的度数.
(2) 如图 7-4 (c) 所示, 在“等邻边四边形” ABCD中, ∠ABC=∠ADC=90°, AB=AD=6, 求对角线AC 的长.
5.定义:如果四边形的某条对角线平分一组对角,那么把这条对角线叫作“美妙线”, 该四边形叫作“美妙四边形”.
如图7-5 所示,在四边形ABDC中,对角线BC平分 和 那么对角线BC为“美妙线”, 四边形ABDC为“美妙四边形”.
(1)下列四边形中是“美妙四边形”的有 .
A.平行四边形 B. 矩形 C. 菱形 D. 正方形
(2) 四边形 ABCD 是“美妙四边形”, 求四边形ABCD的面积.(画出图形并写出解答过程)
6.新定义:有一组对角相等而另一组对角不相等的凸四边形叫作“等对角四边形”.
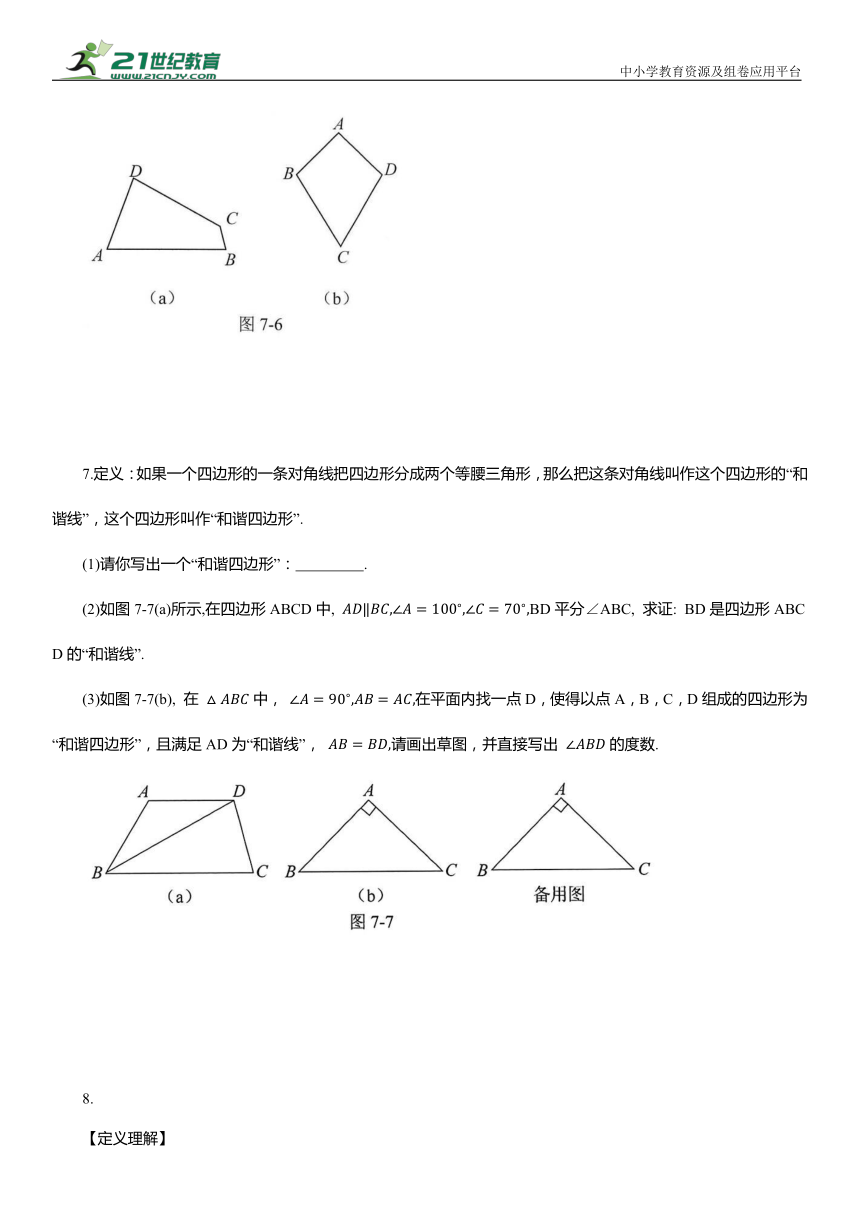
(1)已知: 如图7-6(a)所示,四边形ABCD是“等对角四边形”,∠A≠∠C, 求∠C, ∠ D的度数.
(2)在探究“等对角四边形”的性质时,小红画了一个“等对角四边形”ABCD,如图7-6(b) 所示, 其中 此时她发现( 成立,请你证明此结论.
(3)已知:在“等对角四边形” ABCD中, 求对角线AC的长.
7.定义:如果一个四边形的一条对角线把四边形分成两个等腰三角形,那么把这条对角线叫作这个四边形的“和谐线”,这个四边形叫作“和谐四边形”.
(1)请你写出一个“和谐四边形”: .
(2)如图7-7(a)所示,在四边形ABCD中, BD平分∠ABC, 求证: BD是四边形ABCD的“和谐线”.
(3)如图7-7(b), 在 中, 在平面内找一点D,使得以点A,B,C,D组成的四边形为“和谐四边形”,且满足AD为“和谐线”, 请画出草图,并直接写出 的度数.
8.
【定义理解】
如图7-8(a) 所示, 在△ABC中, 点E是BC的中点, 点P是AE的中点,则称CP是△ABC的“双中线”, ∠ACB=90°, AC=3, AB=5, 则CP= .
【类比探究】
(1) 如图 7-8(b) 所示, 点E是菱形ABCD一边上的中点, 点P是BE上的中点, 则称AP是菱形ABCD的“双中线”. 若AB=4, ∠BAD=120°, 则AP= .
(2)如图7-8(c)所示, AP是矩形ABCD的“双中线”.若AB=4, BC=6,求AP的长.
【拓展应用】
如图7-8(d)所示,AP是平行四边形ABCD的“双中线”.若AB=4,BC=6,∠BAD=120°, 求AP的长.
1. (1)解:正方形、矩形、直角梯形均可.
(2) 证明: ①∵△ABC≌△DBE,
∴BC=BE.
∵∠CBE=60°,
∴△BCE是等边三角形.
②∵△BCE 是等边三角形,
∴BC=CE, ∠BCE=60°.
∵∠DCB=30°,
∴∠DCE=90°.
∵△ABC≌△DBE,
∴DE=AC.
∵在Rt△DCE中,
2.(1)解: 如图38所示,在矩形ABCD中, ∠A, ∠C均为直角, 则矩形ABCD是“美妙四边形”.
故答案为矩形.
证明: (2) 如图39所示, 连接BD.
∵∠C=90°, ∠A=90°,
(3) 如图40 所示, 连接AD.
∵四边形AEDF是“美妙四边形”, ∠A=90°,
∴∠EDF=90°.
∵∠A=90°, AB=AC,
点D为斜边BC上的中点,
∴∠B=∠C=45°, AD⊥BD,
∴∠BDE+∠ADE=∠ADF+∠ADE=90°.
∴∠BDE=∠ADF.
在△BDE和△ADF中,
∴△BDE≌△ADF(ASA).
∴BE=AF.
∴AE+AF=AE+BE=AB, 即AE+AF=AB.
3. (1) 证明: ∵∠BEC=∠AED=90°,
, 即∠BED=∠CEA.
∵BE=EC, AE=ED,
∴△BED≌△CEA(SAS).
∴∠AOD=∠AEG=90°.
∴AC⊥BD.
∴四边形ABCD是“垂美四边形”.
解: 理由如下.
∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°.
∴由勾股定理得,
(3) ∵△BCE和△AED是等腰直角三角形,
故答案为
4. 解:
【概念理解】
(1)在矩形、菱形、平行四边形和梯形中,只有菱形的邻边相等,所以菱形是“等邻边四边形”,故选 B.
(2) ∵BD平分∠ABC,
∴∠ABD=∠DBC.
∵BC∥AD,
∴∠DBC=∠ADB.
∴∠ABD=∠ADB.
∴AB=AD.
∴四边形ABCD是“等邻边四边形”.
故答案为“是”.
【性质探究】
(1) 如图41所示, 连接AC.
∵AB=AD, BC=CD, AC=AC,
∴△ABC≌△ADC(SSS).
∴∠B=∠D.
∵∠BAD=80°, ∠BCD=60°,
(2) 如图42所示, 连接AC.
∵∠ABC=∠ADC=90°, AB=AD, AC=AC,
∴ Rt△ABC≌Rt△ADC(HL).
∴∠BAC=∠DAC.
∵∠DAB=60°,
设AC=x, 则
解得 (不符合题意,舍去).
∴对角线AC的长为
5.解: (1)∵菱形和正方形的每一条对角线平分一组对角,∴菱形和正方形是“美妙四边形”.
故答案为2.
(2)求四边形ABCD的面积有两种情况。
① 当AC是“美妙线”时,如图43所示.
∵AC平分∠BAD和∠BCD, ∠BAD=60°,
∵∠ABC=90°, AB=3+
∵AC=AC, ∠BCA=∠DCA, ∠BCA=∠DAC,
∴△ABC≌△ADC(AAS).
② 当BD是“美妙线”时, 如图44所示, 过点D作DH⊥AB于点H.
∵∠ABC=90°, BD平分∠ABC,
∴∠ABD=∠CBD=45°.
∴△BDH是等腰直角三角形.
∴DH=BH.
∵设AH=a, 则.
解得
∴DH=3.
∵同理可证, △ABD≌△CBD(ASA),
综上所述,四边形ABCD的面积为( 或
6.(1)解:∵四边形ABCD是“等对角四边形”,∠A≠∠C ,∠A=60°,∠B=70°,
(2) 证明: 如图45所示, 连接BD.
∵AB=AD,
∴∠ABD=∠ADB.
∵∠ABC=∠ADC,
∴∠ABC-∠ABD=∠ADC-∠ADB, 即
∴CB=CD.
(3)解:求对角线AC的长分两种情况.
① 当∠ADC=∠ABC=90°时, 延长AD, BC交于点E, 如图46所示.
∵∠ABC=90°, ∠DAB=60°,
∴∠E=30°.
∵ AB=10,
∴AE=2AB=20.
∵ AD=8,
∴DE=AE--AD=20-8=12.
∵∠EDC=90°, ∠E=30°,
② 当∠BCD=∠DAB=60°时,过点D作DM⊥AB于点M , 于点N, 如图47所示.
∵ DM⊥AB, DN⊥BC, ∠ABC=90°,
∴ ∠AMD=90°, 四边形BNDM 是矩形.
∵∠DAB=60°, AD=8, AB=10,
BM =AB-AM =10-4=6.
∵四边形BNDM 是矩形,
∴DN=BM =6, BN=DM =4
∵∠BCD=60°,
综上所述, AC 的长为 或
7.(1)解:根据定义可直接得出,菱形和正方形都是“和谐四边形”.
故答案为菱形 (或正方形).
(2) 证明: ∵AD∥BC, ∠A=100°,
∴∠A+∠ABC=180°, ∠ADB=∠DBC.
∴∠ABC=80°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=∠ADB=40°.
∴AB=AD, 即△ABD是等腰三角形.
∵∠C=70°, ∠DBC=40°,
∴∠BDC=70°.
∴∠C=∠BDC.
∴BD=BC, 即△BDC是等腰三角形.
∴BD把四边形ABCD分成两个等腰三角形,即BD是四边形ABCD的“和谐线”.
(3)解: ∠ABD的大小有以下三种情况.
① 当AD=AC时, 如图48所示.
∵AB=AC, AB=BD,
∴AB=BD=AD, 即△ABD是等边三角形.
∴∠ABD=60°.
② 当AC=CD时, 如图49所示.
∵AB=AC, AB=BD, AD=CD,
∴ AB=BD=AD=CD.
∵∠BAC=90°,
∴四边形ABDC是正方形.
∴∠ABD=90°.
③ 当AD=CD时, 如图 50 所示, 过点D作. 于点M,过点D作DN⊥AB, 交AB的延长线于点N .
∴四边形ANDM 是矩形.
∵ AD=CD,
综上所述,若以点A, B, C, D组成的四边形为“和谐四边形”,且满足AD为“和谐线”,则 的度数为( 或
8. 解:
【定义理解】
∵在 中, ∠ACB=90°, AB=5, AC=3,
∵点E是BC的中点,
∴EC=EB=2.
∵点P是AE的中点,
故答案为
【类比探究】
(1)连接BE,延长BE交AD的延长线于点F,过点B作. 交DA的延长线于点M,如图51所示.
∵四边形ABCD是菱形, AB=4,
∴∠F =∠CBE.
又∵
∴DF=BC=4, EF=BE.
∴AF=8.
∵BM⊥AD,
∴∠ABM =30°.
∴MF=AM+AF=2+8=10.
∵AP是菱形ABCD的“双中线”,
故答案为
(2)如图52所示,连接DP并延长,交AB的延长线于点H.
∵同理可证, △HPB≌△DPE(AAS),
∴在Rt△ADH 中,
∵DP=PH,
【拓展应用】
如图53所示,连接DP,延长DP交AB的延长线于点H.
∵同理可证, △HPB≌△DPE(AAS),
∴DP=PH, DE=BH=2.
∴AH =AB+BH =4+2=6.
∴AD=AH.
∵ 点 P 为DH 中点,
∴ AP⊥DH.
∵四边形ABCD是平行四边形. BC=6,
∴ AD=BC=6.
∵∠BAD=120°,
∴∠DAP=∠HAP=60°.
第7节 新定义四边形
一、知识梳理
深刻理解新定义四边形的性质,围绕性质完成题目要求.
二、分层练习
1.定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为“勾股四边形”.
(1)在你学过的特殊四边形中,写出两种“勾股四边形”的名称;
(2) 如图 7-1 所示, 将 绕顶点B 按顺时针方向旋转( 得到 连接AD,DC , CE, 已知
① 求证: 是等边三角形;
② 求证: 即四边形ABCD是“勾股四边形”.
2. 如图 7-2(a) 所示, 在四边形ABCD中, 若∠A, ∠C均为直角, 则称这样的四边形为“美妙四边形”.
(1)在“平行四边形、矩形、菱形”中, 一定是“美妙四边形”.(填写图形名称)
(2) 试证明:
(3) 如图7-2(b) 所示, 在等腰直角三角形ABC中, 点D为BC的中点, 点E, F分别在AB, AC 上, 连接DE, DF, 如果四边形AEDF 是“美妙四边形”,试证明:
3.我们定义对角线互相垂直的四边形叫作“垂美四边形”.
如图 7-3 所示, 点E 是四边形ABCD内一点, 已知 ,对角线AC 与BD相交于O点,BD与EC相交于点F,AC与ED相交于点G .
(1)求证: 四边形ABCD是“垂美四边形”.
(2)猜想四边形ABCD两组对边AB,CD与BC,AD之间的数量关系并说明理由.
(3) 若. , 则CD的长为 .
4.定义:有一组邻边相等的凸四边形叫作“等邻边四边形”.
【概念理解】
(1)下列四边形中是“等邻边四边形”的是 .
A. 矩形 B. 菱形 C.平行四边形 D. 梯形
(2)如图7-4(a)所示, 在四边形ABCD中, 若∠ABC=∠BCD, BC∥AD,对角线BD平分∠ABC, 则四边形ABCD “等邻边四边形”. (填“是”或“不是”)
【性质探究】
(1)小红画了一个“等邻边四边形” ABCD,如图7-4(b)所示,其中AB=AD,BC=CD. 若∠A=80°, ∠C=60°, 求出∠B, ∠D的度数.
(2) 如图 7-4 (c) 所示, 在“等邻边四边形” ABCD中, ∠ABC=∠ADC=90°, AB=AD=6, 求对角线AC 的长.
5.定义:如果四边形的某条对角线平分一组对角,那么把这条对角线叫作“美妙线”, 该四边形叫作“美妙四边形”.
如图7-5 所示,在四边形ABDC中,对角线BC平分 和 那么对角线BC为“美妙线”, 四边形ABDC为“美妙四边形”.
(1)下列四边形中是“美妙四边形”的有 .
A.平行四边形 B. 矩形 C. 菱形 D. 正方形
(2) 四边形 ABCD 是“美妙四边形”, 求四边形ABCD的面积.(画出图形并写出解答过程)
6.新定义:有一组对角相等而另一组对角不相等的凸四边形叫作“等对角四边形”.
(1)已知: 如图7-6(a)所示,四边形ABCD是“等对角四边形”,∠A≠∠C, 求∠C, ∠ D的度数.
(2)在探究“等对角四边形”的性质时,小红画了一个“等对角四边形”ABCD,如图7-6(b) 所示, 其中 此时她发现( 成立,请你证明此结论.
(3)已知:在“等对角四边形” ABCD中, 求对角线AC的长.
7.定义:如果一个四边形的一条对角线把四边形分成两个等腰三角形,那么把这条对角线叫作这个四边形的“和谐线”,这个四边形叫作“和谐四边形”.
(1)请你写出一个“和谐四边形”: .
(2)如图7-7(a)所示,在四边形ABCD中, BD平分∠ABC, 求证: BD是四边形ABCD的“和谐线”.
(3)如图7-7(b), 在 中, 在平面内找一点D,使得以点A,B,C,D组成的四边形为“和谐四边形”,且满足AD为“和谐线”, 请画出草图,并直接写出 的度数.
8.
【定义理解】
如图7-8(a) 所示, 在△ABC中, 点E是BC的中点, 点P是AE的中点,则称CP是△ABC的“双中线”, ∠ACB=90°, AC=3, AB=5, 则CP= .
【类比探究】
(1) 如图 7-8(b) 所示, 点E是菱形ABCD一边上的中点, 点P是BE上的中点, 则称AP是菱形ABCD的“双中线”. 若AB=4, ∠BAD=120°, 则AP= .
(2)如图7-8(c)所示, AP是矩形ABCD的“双中线”.若AB=4, BC=6,求AP的长.
【拓展应用】
如图7-8(d)所示,AP是平行四边形ABCD的“双中线”.若AB=4,BC=6,∠BAD=120°, 求AP的长.
1. (1)解:正方形、矩形、直角梯形均可.
(2) 证明: ①∵△ABC≌△DBE,
∴BC=BE.
∵∠CBE=60°,
∴△BCE是等边三角形.
②∵△BCE 是等边三角形,
∴BC=CE, ∠BCE=60°.
∵∠DCB=30°,
∴∠DCE=90°.
∵△ABC≌△DBE,
∴DE=AC.
∵在Rt△DCE中,
2.(1)解: 如图38所示,在矩形ABCD中, ∠A, ∠C均为直角, 则矩形ABCD是“美妙四边形”.
故答案为矩形.
证明: (2) 如图39所示, 连接BD.
∵∠C=90°, ∠A=90°,
(3) 如图40 所示, 连接AD.
∵四边形AEDF是“美妙四边形”, ∠A=90°,
∴∠EDF=90°.
∵∠A=90°, AB=AC,
点D为斜边BC上的中点,
∴∠B=∠C=45°, AD⊥BD,
∴∠BDE+∠ADE=∠ADF+∠ADE=90°.
∴∠BDE=∠ADF.
在△BDE和△ADF中,
∴△BDE≌△ADF(ASA).
∴BE=AF.
∴AE+AF=AE+BE=AB, 即AE+AF=AB.
3. (1) 证明: ∵∠BEC=∠AED=90°,
, 即∠BED=∠CEA.
∵BE=EC, AE=ED,
∴△BED≌△CEA(SAS).
∴∠AOD=∠AEG=90°.
∴AC⊥BD.
∴四边形ABCD是“垂美四边形”.
解: 理由如下.
∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°.
∴由勾股定理得,
(3) ∵△BCE和△AED是等腰直角三角形,
故答案为
4. 解:
【概念理解】
(1)在矩形、菱形、平行四边形和梯形中,只有菱形的邻边相等,所以菱形是“等邻边四边形”,故选 B.
(2) ∵BD平分∠ABC,
∴∠ABD=∠DBC.
∵BC∥AD,
∴∠DBC=∠ADB.
∴∠ABD=∠ADB.
∴AB=AD.
∴四边形ABCD是“等邻边四边形”.
故答案为“是”.
【性质探究】
(1) 如图41所示, 连接AC.
∵AB=AD, BC=CD, AC=AC,
∴△ABC≌△ADC(SSS).
∴∠B=∠D.
∵∠BAD=80°, ∠BCD=60°,
(2) 如图42所示, 连接AC.
∵∠ABC=∠ADC=90°, AB=AD, AC=AC,
∴ Rt△ABC≌Rt△ADC(HL).
∴∠BAC=∠DAC.
∵∠DAB=60°,
设AC=x, 则
解得 (不符合题意,舍去).
∴对角线AC的长为
5.解: (1)∵菱形和正方形的每一条对角线平分一组对角,∴菱形和正方形是“美妙四边形”.
故答案为2.
(2)求四边形ABCD的面积有两种情况。
① 当AC是“美妙线”时,如图43所示.
∵AC平分∠BAD和∠BCD, ∠BAD=60°,
∵∠ABC=90°, AB=3+
∵AC=AC, ∠BCA=∠DCA, ∠BCA=∠DAC,
∴△ABC≌△ADC(AAS).
② 当BD是“美妙线”时, 如图44所示, 过点D作DH⊥AB于点H.
∵∠ABC=90°, BD平分∠ABC,
∴∠ABD=∠CBD=45°.
∴△BDH是等腰直角三角形.
∴DH=BH.
∵设AH=a, 则.
解得
∴DH=3.
∵同理可证, △ABD≌△CBD(ASA),
综上所述,四边形ABCD的面积为( 或
6.(1)解:∵四边形ABCD是“等对角四边形”,∠A≠∠C ,∠A=60°,∠B=70°,
(2) 证明: 如图45所示, 连接BD.
∵AB=AD,
∴∠ABD=∠ADB.
∵∠ABC=∠ADC,
∴∠ABC-∠ABD=∠ADC-∠ADB, 即
∴CB=CD.
(3)解:求对角线AC的长分两种情况.
① 当∠ADC=∠ABC=90°时, 延长AD, BC交于点E, 如图46所示.
∵∠ABC=90°, ∠DAB=60°,
∴∠E=30°.
∵ AB=10,
∴AE=2AB=20.
∵ AD=8,
∴DE=AE--AD=20-8=12.
∵∠EDC=90°, ∠E=30°,
② 当∠BCD=∠DAB=60°时,过点D作DM⊥AB于点M , 于点N, 如图47所示.
∵ DM⊥AB, DN⊥BC, ∠ABC=90°,
∴ ∠AMD=90°, 四边形BNDM 是矩形.
∵∠DAB=60°, AD=8, AB=10,
BM =AB-AM =10-4=6.
∵四边形BNDM 是矩形,
∴DN=BM =6, BN=DM =4
∵∠BCD=60°,
综上所述, AC 的长为 或
7.(1)解:根据定义可直接得出,菱形和正方形都是“和谐四边形”.
故答案为菱形 (或正方形).
(2) 证明: ∵AD∥BC, ∠A=100°,
∴∠A+∠ABC=180°, ∠ADB=∠DBC.
∴∠ABC=80°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=∠ADB=40°.
∴AB=AD, 即△ABD是等腰三角形.
∵∠C=70°, ∠DBC=40°,
∴∠BDC=70°.
∴∠C=∠BDC.
∴BD=BC, 即△BDC是等腰三角形.
∴BD把四边形ABCD分成两个等腰三角形,即BD是四边形ABCD的“和谐线”.
(3)解: ∠ABD的大小有以下三种情况.
① 当AD=AC时, 如图48所示.
∵AB=AC, AB=BD,
∴AB=BD=AD, 即△ABD是等边三角形.
∴∠ABD=60°.
② 当AC=CD时, 如图49所示.
∵AB=AC, AB=BD, AD=CD,
∴ AB=BD=AD=CD.
∵∠BAC=90°,
∴四边形ABDC是正方形.
∴∠ABD=90°.
③ 当AD=CD时, 如图 50 所示, 过点D作. 于点M,过点D作DN⊥AB, 交AB的延长线于点N .
∴四边形ANDM 是矩形.
∵ AD=CD,
综上所述,若以点A, B, C, D组成的四边形为“和谐四边形”,且满足AD为“和谐线”,则 的度数为( 或
8. 解:
【定义理解】
∵在 中, ∠ACB=90°, AB=5, AC=3,
∵点E是BC的中点,
∴EC=EB=2.
∵点P是AE的中点,
故答案为
【类比探究】
(1)连接BE,延长BE交AD的延长线于点F,过点B作. 交DA的延长线于点M,如图51所示.
∵四边形ABCD是菱形, AB=4,
∴∠F =∠CBE.
又∵
∴DF=BC=4, EF=BE.
∴AF=8.
∵BM⊥AD,
∴∠ABM =30°.
∴MF=AM+AF=2+8=10.
∵AP是菱形ABCD的“双中线”,
故答案为
(2)如图52所示,连接DP并延长,交AB的延长线于点H.
∵同理可证, △HPB≌△DPE(AAS),
∴在Rt△ADH 中,
∵DP=PH,
【拓展应用】
如图53所示,连接DP,延长DP交AB的延长线于点H.
∵同理可证, △HPB≌△DPE(AAS),
∴DP=PH, DE=BH=2.
∴AH =AB+BH =4+2=6.
∴AD=AH.
∵ 点 P 为DH 中点,
∴ AP⊥DH.
∵四边形ABCD是平行四边形. BC=6,
∴ AD=BC=6.
∵∠BAD=120°,
∴∠DAP=∠HAP=60°.
