四边形与动点 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 四边形与动点 同步练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 344.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:41:05 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第8节 四边形与动点
一、方法总结
1.用含未知数的式子表示线段长度,明确未知数的取值范围.
2.根据题目要求选择合适的四边形判定定理.
3.根据不同的取值范围分类讨论.
二、分层练习
☆万丈高楼平地起
1. 如图 8-1 所示, 在四边形ABCD中, 点M 是BC上一点,且BM=9cm,点E从点A出发以1cm/s的速度向点D运动,点F 从点C 出发, 以3cm/s的速度向点B运动,当其中一点到达终点时,另一点也随之停止. 设运动时间为 ts,则当以点A, M, E, F为顶点的四边形是平行四边形时, t的值是( ).
A.
B. 3
C. 3或
D.
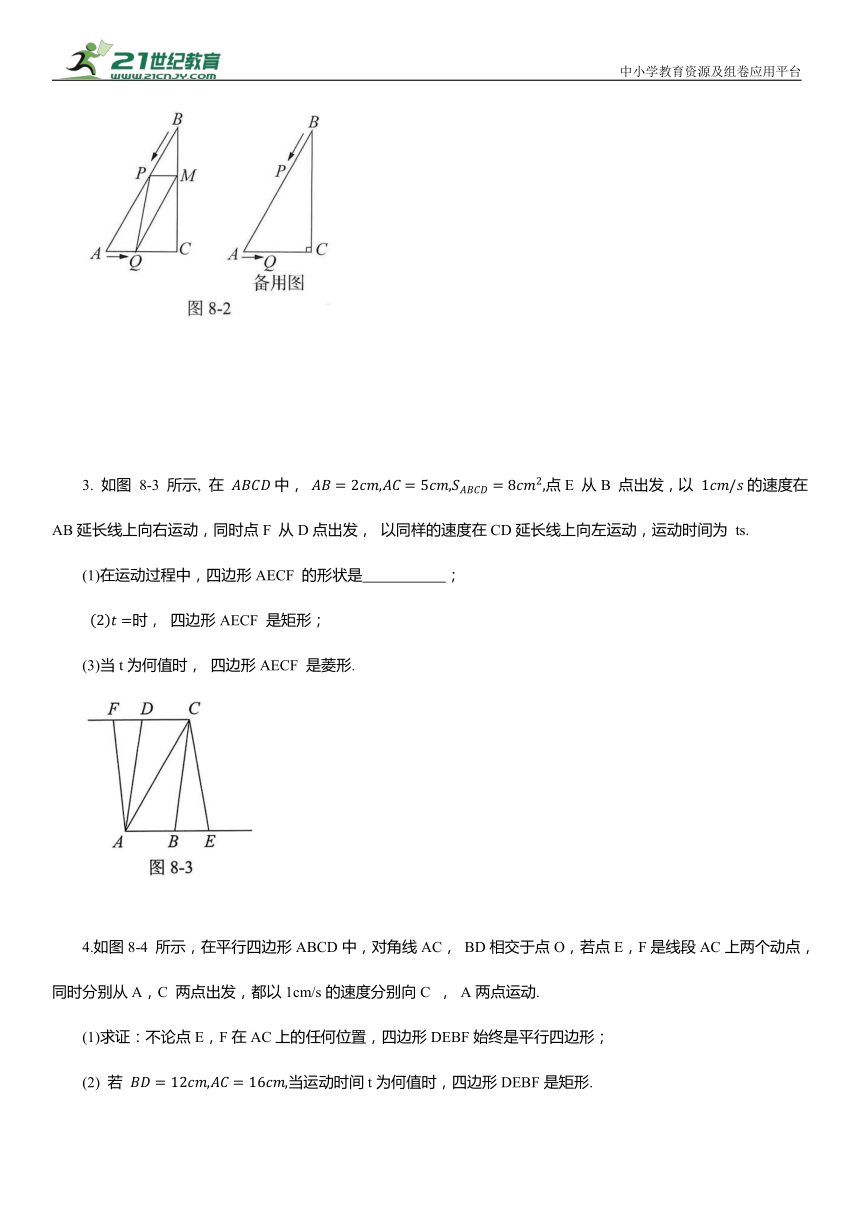
2. 如图8-2所示, 在 中, 点P从点B出发沿BA方向以每秒2个单位长度的速度向点A匀速运动,同时点Q从点A出发沿AC 方向以每秒1个单位长度的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P, Q运动的时间是 ts,过点P作 于点M , 连接PQ, QM.
(1)请用含有t的式子填空:
(2)是否存在某一时刻,使四边形AQMP为菱形 如果存在,求出相应的t值;如果不存在,说明理由.
3. 如图 8-3 所示, 在 中, 点E 从B 点出发,以 的速度在AB延长线上向右运动,同时点F 从D点出发, 以同样的速度在CD延长线上向左运动,运动时间为 ts.
(1)在运动过程中,四边形AECF 的形状是 ;
时, 四边形AECF 是矩形;
(3)当t为何值时, 四边形AECF 是菱形.
4.如图8-4 所示,在平行四边形ABCD中,对角线AC, BD相交于点O,若点E,F是线段AC上两个动点,同时分别从A,C 两点出发,都以1cm/s的速度分别向C , A两点运动.
(1)求证:不论点E,F在AC上的任何位置,四边形DEBF始终是平行四边形;
(2) 若 当运动时间t为何值时,四边形DEBF是矩形.
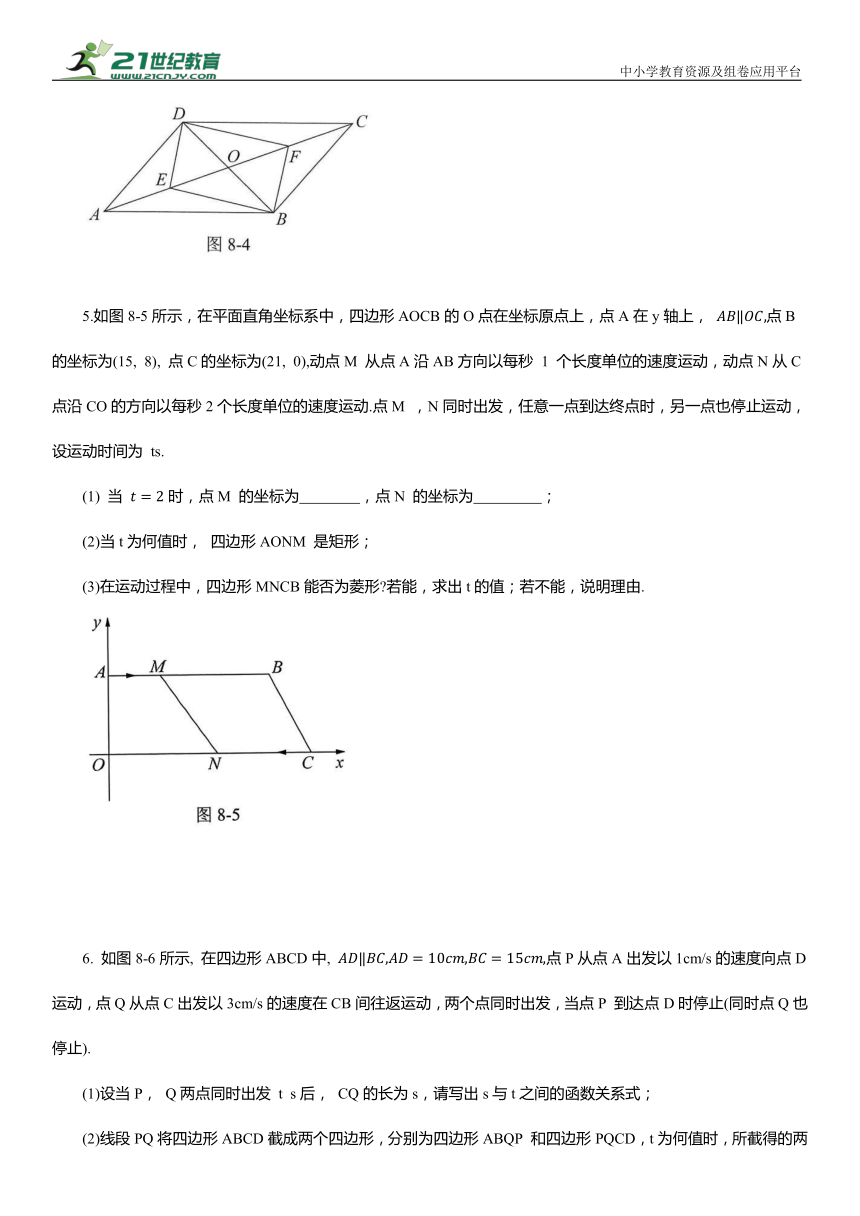
5.如图8-5所示,在平面直角坐标系中,四边形AOCB的O点在坐标原点上,点A在y轴上, 点B 的坐标为(15, 8), 点C的坐标为(21, 0),动点M 从点A沿AB方向以每秒 1 个长度单位的速度运动,动点N从C点沿CO的方向以每秒2个长度单位的速度运动.点M ,N同时出发,任意一点到达终点时,另一点也停止运动,设运动时间为 ts.
(1) 当 时,点M 的坐标为 ,点N 的坐标为 ;
(2)当t为何值时, 四边形AONM 是矩形;
(3)在运动过程中,四边形MNCB能否为菱形 若能,求出t的值;若不能,说明理由.
6. 如图8-6所示, 在四边形ABCD中, 点P从点A出发以1cm/s的速度向点D运动,点Q从点C出发以3cm/s的速度在CB间往返运动,两个点同时出发,当点P 到达点D时停止(同时点Q也停止).
(1)设当P, Q两点同时出发 t s后, CQ的长为s,请写出s与t之间的函数关系式;
(2)线段PQ将四边形ABCD截成两个四边形,分别为四边形ABQP 和四边形PQCD,t为何值时,所截得的两个四边形中,其中一个四边形为平行四边形.
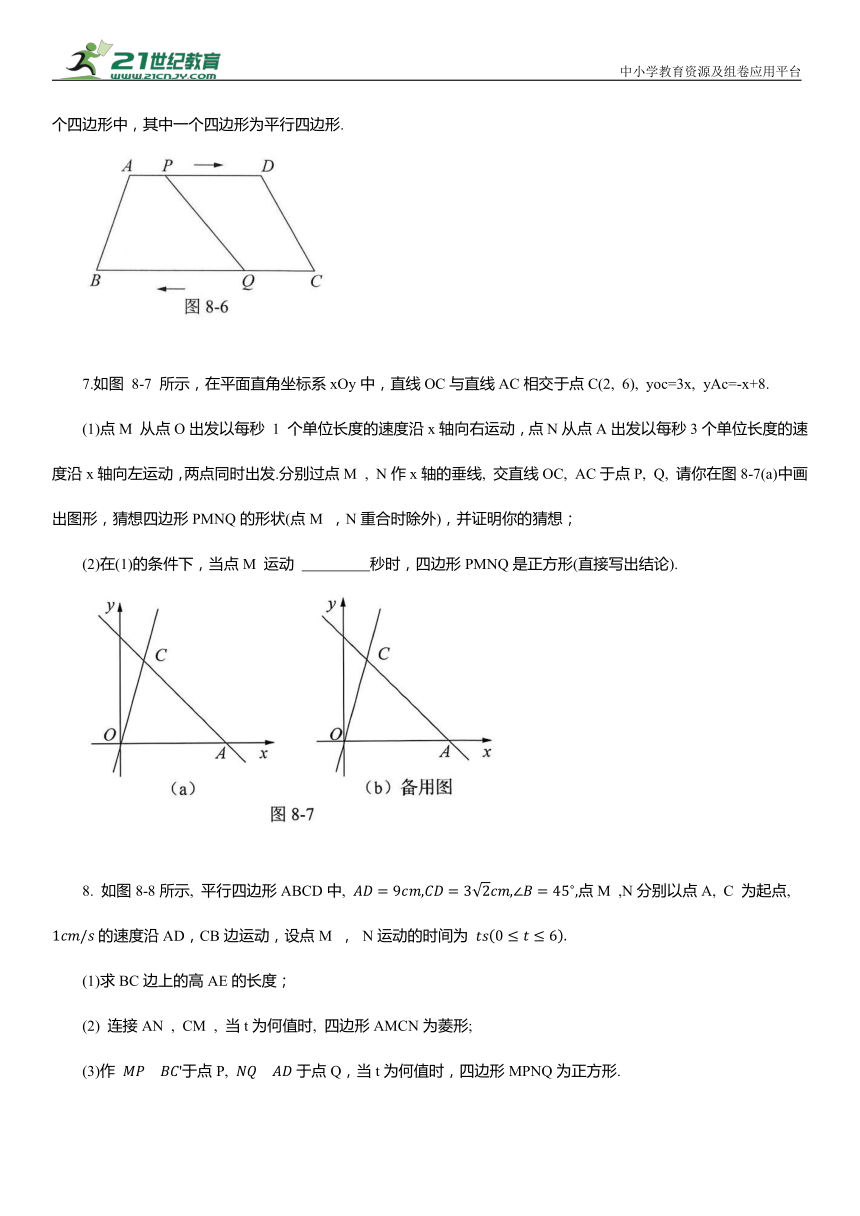
7.如图 8-7 所示,在平面直角坐标系xOy中,直线OC与直线AC相交于点C(2, 6), yoc=3x, yAc=-x+8.
(1)点M 从点O出发以每秒 1 个单位长度的速度沿x轴向右运动,点N从点A出发以每秒3个单位长度的速度沿x轴向左运动,两点同时出发.分别过点M , N作x轴的垂线, 交直线OC, AC于点P, Q, 请你在图8-7(a)中画出图形,猜想四边形PMNQ的形状(点M ,N重合时除外),并证明你的猜想;
(2)在(1)的条件下,当点M 运动 秒时,四边形PMNQ是正方形(直接写出结论).
8. 如图8-8所示, 平行四边形ABCD中, 点M ,N分别以点A, C 为起点, 的速度沿AD,CB边运动,设点M , N运动的时间为
(1)求BC边上的高AE的长度;
(2) 连接AN , CM , 当t为何值时, 四边形AMCN为菱形;
(3)作 '于点P, 于点Q,当t为何值时,四边形MPNQ为正方形.
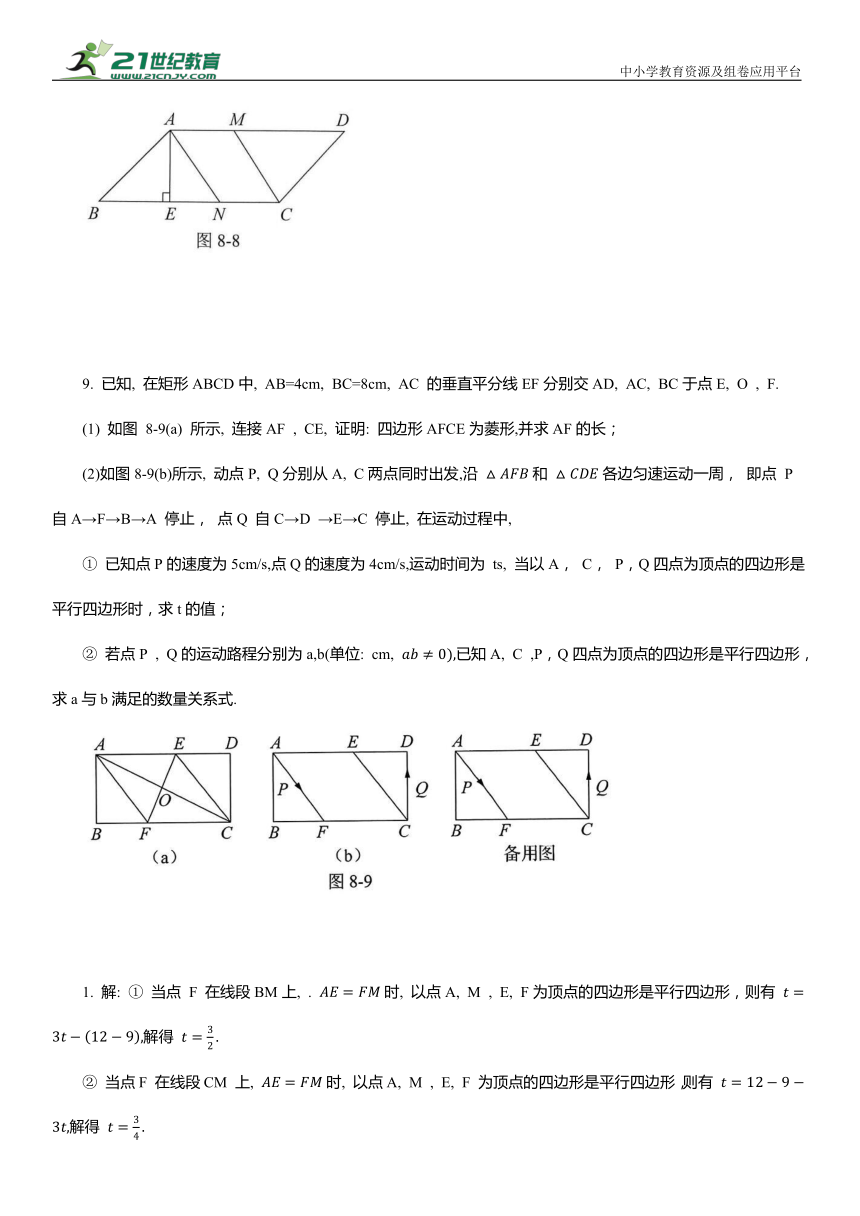
9. 已知, 在矩形ABCD中, AB=4cm, BC=8cm, AC 的垂直平分线EF分别交AD, AC, BC于点E, O , F.
(1) 如图 8-9(a) 所示, 连接AF , CE, 证明: 四边形AFCE为菱形,并求AF的长;
(2)如图8-9(b)所示, 动点P, Q分别从A, C两点同时出发,沿 和 各边匀速运动一周, 即点 P 自A→F→B→A 停止, 点Q 自C→D →E→C 停止, 在运动过程中,
① 已知点P的速度为5cm/s,点Q的速度为4cm/s,运动时间为 ts, 当以A, C, P,Q四点为顶点的四边形是平行四边形时,求t的值;
② 若点P , Q的运动路程分别为a,b(单位: cm, 已知A, C ,P,Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
1. 解: ① 当点 F 在线段BM上, . 时, 以点A, M , E, F为顶点的四边形是平行四边形,则有 解得
② 当点F 在线段CM 上, 时, 以点A, M , E, F 为顶点的四边形是平行四边形,则有 解得
综上所述, 或 时,以点A,M,E,F为顶点的四边形是平行四边形.
故选 D.
2. 解:
(1)∵点Q从点A出发沿AC 方向以每秒1个单位长度的速度向点C匀速运动,设运动时间为t,
(2)存在,理由如下:
又∵由 (1) 知,
∴四边形AQMP 是平行四边形.
∴当 时, 平行四边形AQMP是菱形.
即
时,平行四边形AQMP为菱形.
∴AB=2AC=40.
∴AP=AB-BP=40-2t.
∵PM⊥BC,
∴∠PMB=90°.
故答案为t, 40-2t, t.
3. 解: (1) 四边形 AECF 是平行四边形.
∵四边形ABCD是平行四边形,
∴AB=CD=2cm, AB∥CD.
∴CF∥AE.
∵DF=BE.
∴CF=AE .
∴四边形AECF 是平行四边形.
时,四边形AECF 是矩形.
∵四边形AECF 是矩形,
∵在 中,
即
或 (舍去).
(3) 过点C作CG⊥BE于点G, 如图54所示.
∵由 (1)知,四边形AECF 是平行四边形,
∴ AE=CE时, 四边形AECF 是菱形.
又∵BE= tcm,
∴AE=CE=t+2(cm).
∴CG=4cm.
∴GE=t+2-3=t-1(cm).
∵在Rt△CGE中, 即
时, 四边形AECF 是菱形.
4. (1) 证明: 设运动时间为t, 则AE=CF =t.
∵四边形ABCD是平行四边形,
∴AO=CO, BO=DO.
∴EO=FO.
∴四边形DEBF是平行四边形.
(2) 解:
∴当OE=OB时, 四边形DEBF 是矩形.
∴i) 当点E在AO上时, 8-t=6, 解得t=2;
ii) 当点E在OC上时, t-8=6, 解得t=14.
∴当t=2s或t=14s时, 四边形DEBF 是矩形.
5. 解: (1) ∵点B的坐标为(15,8), 点C的坐标为(21,0), 动点M 从点A沿AB方向以每秒1个长度单位的速度运动,动点N从C点沿CO的方向以每秒2个长度单位的速度运动, t=2,
∴AM=2, CN=4.
∴ON=21-4=17.
∴点M 的坐标为(2, 8), 点N的坐标为(17, 0).
(2) 过点B作BD⊥OC于点D, 如图55所示, 则四边形AODB是矩形.
∵当四边形AONM 是矩形时, AM =ON ,
∴t=21-2t, 解得t=7.
∴t=7时, 四边形AONM 是矩形.
(3) t=5时, 四边形MNCB为菱形.
∵四边形MNCB 为平行四边形时,BM=CN,
∴15-t=2t, 解得t=5.
∴CN=5×2=10.
∵四边形AODB 是矩形,
∴OD=AB=15, BD=OA=8, CD=OC-OD=6.
∵在Rt△BCD中,
∴BC=CN.
∴平行四边形MNCB 是菱形.
6. 解: (1) ∵点P从点A出发以1cm/s的速度向点D运动,
∴点P到达点D的时间
∴当0当5≤t<10时, CQ=s=30-3t.
(2) 当0若四边形PQCD是平行四边形, 则PD=CQ, 10-t=3t, 解得
若四边形ABQP 是平行四边形, 则AP=BQ, t=15-3t, 解得
当5≤t<10时,
若四边形PQCD是平行四边形,则PD=CQ,10-t=30-3t,解得t=10(不合题意,舍去).
若四边形ABQP 是平行四边形, 则AP=BQ, t=3t-15, 解得
7. 解: (1) 如图56所示, 四边形PMNQ为矩形.
∵点A在直线AC上,
∴当y=0时, x=8, 即A(8, 0).
设点 M 的运动时间为 m s, 则OM =m ,AN=3m.
∵点M , N在x轴上,
∴M(m, 0), N(8-3m, 0).
∵PM⊥x轴, QN⊥x轴,
∴∠PMA=∠QNA=90°.
∴PM∥QN.
∵点P在直线OC上, yoc=3x,
点Q在直线AC上,
∴P(m, 3m), Q(8-3m, 3m).
∴PM=QN.
∴四边形PMNQ为平行四边形.
又∵∠PMA=90°,
∴四边形PMNQ为矩形.
(2) ∵四边形PMNQ是正方形,
∴MN=QN, 即8-4m=|3m|, 解得 或8.
∴当点M 运动 或8s时,四边形PMNQ是正方形.
故答案为 或8.
8. 解: (1) ∵四边形ABCD是平行四边形,
∵在Rt△ABE中, ∠AEB=90°, ∠B=45°,
∴AE=3cm.
(2) ∵点M, N分别以A, C为起点, 1cm/s的速度沿AD, CB边运动,设点M , N运动的时间为 ts(0≤t≤6),
∴AM =CN =t.
∵AM∥CN,
∴四边形AMCN 为平行四边形.
∴当AN =AM 时, 四边形AMCN为菱形.
∵BE=AE=3, EN=6-t,
解得
故当 时, 四边形AMCN为菱形
(3)按照题干要求作图,如图57所示.
∵MP⊥BC于点P, NQ⊥AD于点Q,
∴四边形MPNQ为矩形.
∴当QM=QN时, 四边形MPNQ为正方形.
∵AM =CN=t, BE=3,
∴AQ=EN=BC-BE-CN=9-3-t=6-t.
(注:点Q在点M 的左侧或右侧).
∵QN=AE=3,
∴|2t-6|=3, 解得t=4.5或t=1.5.
故当t=4.5或t=1.5时, 四边形MPNQ为正方形.
23会当凌绝顶,一览众山小
9. 解: (1) ∵四边形ABCD是矩形,
∴AD∥BC.
∴∠CAD=∠ACB , ∠AEF=∠CFE.
∵EF 垂直平分AC,垂足为点O,
∴OA=OC.
∴△AOE≌△COF(AAS).
∴OE=OF.
∴四边形AFCE为平行四边形.
又∵EF⊥AC,
∴四边形AFCE为菱形.
设菱形的边长 , 则
∵在Rt△ABF中, AB=4cm,
解得x=5.
∴AF=5cm.
(2) ①当点P在AF上时, Q点在CD上, A, C, P, Q四点不构成平行四边形.
同理, 点P在AB上时, Q点在DE或CE上, A, C, P, Q四点不构成平行四边形.
点P在BF上,点Q在CD上时, A, C, P, Q四点不构成平行四边形.
只有当点P在BF上,点Q在ED上时,才能构成平行四边形.
综上所述,以A,C,P,Q四点为顶点的四边形是平行四边形时,
∵点P 的速度为5cm/s,点Q的速度为 运动时间为 ts,
∴5t=12-4t, 解得
∴以A, C, P, Q四点为顶点的四边形是平行四边形时,
② 由题意得,四边形APCQ是平行四边形时,点P,Q在互相平行的对应边上,有以下三种情况.
如图58所示,当点P在AF上,点Q在CE上时, 即a=12-b,得a+b=12.
如图59所示,当点P在BF上,点Q在DE上时,. 即12-b=a,得a+b=12.
如图60所示,当点P在AB上,点Q在CD上时, 即 得a+b=12.
综上所述,a与b满足的数量关系式是
第8节 四边形与动点
一、方法总结
1.用含未知数的式子表示线段长度,明确未知数的取值范围.
2.根据题目要求选择合适的四边形判定定理.
3.根据不同的取值范围分类讨论.
二、分层练习
☆万丈高楼平地起
1. 如图 8-1 所示, 在四边形ABCD中, 点M 是BC上一点,且BM=9cm,点E从点A出发以1cm/s的速度向点D运动,点F 从点C 出发, 以3cm/s的速度向点B运动,当其中一点到达终点时,另一点也随之停止. 设运动时间为 ts,则当以点A, M, E, F为顶点的四边形是平行四边形时, t的值是( ).
A.
B. 3
C. 3或
D.
2. 如图8-2所示, 在 中, 点P从点B出发沿BA方向以每秒2个单位长度的速度向点A匀速运动,同时点Q从点A出发沿AC 方向以每秒1个单位长度的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P, Q运动的时间是 ts,过点P作 于点M , 连接PQ, QM.
(1)请用含有t的式子填空:
(2)是否存在某一时刻,使四边形AQMP为菱形 如果存在,求出相应的t值;如果不存在,说明理由.
3. 如图 8-3 所示, 在 中, 点E 从B 点出发,以 的速度在AB延长线上向右运动,同时点F 从D点出发, 以同样的速度在CD延长线上向左运动,运动时间为 ts.
(1)在运动过程中,四边形AECF 的形状是 ;
时, 四边形AECF 是矩形;
(3)当t为何值时, 四边形AECF 是菱形.
4.如图8-4 所示,在平行四边形ABCD中,对角线AC, BD相交于点O,若点E,F是线段AC上两个动点,同时分别从A,C 两点出发,都以1cm/s的速度分别向C , A两点运动.
(1)求证:不论点E,F在AC上的任何位置,四边形DEBF始终是平行四边形;
(2) 若 当运动时间t为何值时,四边形DEBF是矩形.
5.如图8-5所示,在平面直角坐标系中,四边形AOCB的O点在坐标原点上,点A在y轴上, 点B 的坐标为(15, 8), 点C的坐标为(21, 0),动点M 从点A沿AB方向以每秒 1 个长度单位的速度运动,动点N从C点沿CO的方向以每秒2个长度单位的速度运动.点M ,N同时出发,任意一点到达终点时,另一点也停止运动,设运动时间为 ts.
(1) 当 时,点M 的坐标为 ,点N 的坐标为 ;
(2)当t为何值时, 四边形AONM 是矩形;
(3)在运动过程中,四边形MNCB能否为菱形 若能,求出t的值;若不能,说明理由.
6. 如图8-6所示, 在四边形ABCD中, 点P从点A出发以1cm/s的速度向点D运动,点Q从点C出发以3cm/s的速度在CB间往返运动,两个点同时出发,当点P 到达点D时停止(同时点Q也停止).
(1)设当P, Q两点同时出发 t s后, CQ的长为s,请写出s与t之间的函数关系式;
(2)线段PQ将四边形ABCD截成两个四边形,分别为四边形ABQP 和四边形PQCD,t为何值时,所截得的两个四边形中,其中一个四边形为平行四边形.
7.如图 8-7 所示,在平面直角坐标系xOy中,直线OC与直线AC相交于点C(2, 6), yoc=3x, yAc=-x+8.
(1)点M 从点O出发以每秒 1 个单位长度的速度沿x轴向右运动,点N从点A出发以每秒3个单位长度的速度沿x轴向左运动,两点同时出发.分别过点M , N作x轴的垂线, 交直线OC, AC于点P, Q, 请你在图8-7(a)中画出图形,猜想四边形PMNQ的形状(点M ,N重合时除外),并证明你的猜想;
(2)在(1)的条件下,当点M 运动 秒时,四边形PMNQ是正方形(直接写出结论).
8. 如图8-8所示, 平行四边形ABCD中, 点M ,N分别以点A, C 为起点, 的速度沿AD,CB边运动,设点M , N运动的时间为
(1)求BC边上的高AE的长度;
(2) 连接AN , CM , 当t为何值时, 四边形AMCN为菱形;
(3)作 '于点P, 于点Q,当t为何值时,四边形MPNQ为正方形.
9. 已知, 在矩形ABCD中, AB=4cm, BC=8cm, AC 的垂直平分线EF分别交AD, AC, BC于点E, O , F.
(1) 如图 8-9(a) 所示, 连接AF , CE, 证明: 四边形AFCE为菱形,并求AF的长;
(2)如图8-9(b)所示, 动点P, Q分别从A, C两点同时出发,沿 和 各边匀速运动一周, 即点 P 自A→F→B→A 停止, 点Q 自C→D →E→C 停止, 在运动过程中,
① 已知点P的速度为5cm/s,点Q的速度为4cm/s,运动时间为 ts, 当以A, C, P,Q四点为顶点的四边形是平行四边形时,求t的值;
② 若点P , Q的运动路程分别为a,b(单位: cm, 已知A, C ,P,Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
1. 解: ① 当点 F 在线段BM上, . 时, 以点A, M , E, F为顶点的四边形是平行四边形,则有 解得
② 当点F 在线段CM 上, 时, 以点A, M , E, F 为顶点的四边形是平行四边形,则有 解得
综上所述, 或 时,以点A,M,E,F为顶点的四边形是平行四边形.
故选 D.
2. 解:
(1)∵点Q从点A出发沿AC 方向以每秒1个单位长度的速度向点C匀速运动,设运动时间为t,
(2)存在,理由如下:
又∵由 (1) 知,
∴四边形AQMP 是平行四边形.
∴当 时, 平行四边形AQMP是菱形.
即
时,平行四边形AQMP为菱形.
∴AB=2AC=40.
∴AP=AB-BP=40-2t.
∵PM⊥BC,
∴∠PMB=90°.
故答案为t, 40-2t, t.
3. 解: (1) 四边形 AECF 是平行四边形.
∵四边形ABCD是平行四边形,
∴AB=CD=2cm, AB∥CD.
∴CF∥AE.
∵DF=BE.
∴CF=AE .
∴四边形AECF 是平行四边形.
时,四边形AECF 是矩形.
∵四边形AECF 是矩形,
∵在 中,
即
或 (舍去).
(3) 过点C作CG⊥BE于点G, 如图54所示.
∵由 (1)知,四边形AECF 是平行四边形,
∴ AE=CE时, 四边形AECF 是菱形.
又∵BE= tcm,
∴AE=CE=t+2(cm).
∴CG=4cm.
∴GE=t+2-3=t-1(cm).
∵在Rt△CGE中, 即
时, 四边形AECF 是菱形.
4. (1) 证明: 设运动时间为t, 则AE=CF =t.
∵四边形ABCD是平行四边形,
∴AO=CO, BO=DO.
∴EO=FO.
∴四边形DEBF是平行四边形.
(2) 解:
∴当OE=OB时, 四边形DEBF 是矩形.
∴i) 当点E在AO上时, 8-t=6, 解得t=2;
ii) 当点E在OC上时, t-8=6, 解得t=14.
∴当t=2s或t=14s时, 四边形DEBF 是矩形.
5. 解: (1) ∵点B的坐标为(15,8), 点C的坐标为(21,0), 动点M 从点A沿AB方向以每秒1个长度单位的速度运动,动点N从C点沿CO的方向以每秒2个长度单位的速度运动, t=2,
∴AM=2, CN=4.
∴ON=21-4=17.
∴点M 的坐标为(2, 8), 点N的坐标为(17, 0).
(2) 过点B作BD⊥OC于点D, 如图55所示, 则四边形AODB是矩形.
∵当四边形AONM 是矩形时, AM =ON ,
∴t=21-2t, 解得t=7.
∴t=7时, 四边形AONM 是矩形.
(3) t=5时, 四边形MNCB为菱形.
∵四边形MNCB 为平行四边形时,BM=CN,
∴15-t=2t, 解得t=5.
∴CN=5×2=10.
∵四边形AODB 是矩形,
∴OD=AB=15, BD=OA=8, CD=OC-OD=6.
∵在Rt△BCD中,
∴BC=CN.
∴平行四边形MNCB 是菱形.
6. 解: (1) ∵点P从点A出发以1cm/s的速度向点D运动,
∴点P到达点D的时间
∴当0
(2) 当0
若四边形ABQP 是平行四边形, 则AP=BQ, t=15-3t, 解得
当5≤t<10时,
若四边形PQCD是平行四边形,则PD=CQ,10-t=30-3t,解得t=10(不合题意,舍去).
若四边形ABQP 是平行四边形, 则AP=BQ, t=3t-15, 解得
7. 解: (1) 如图56所示, 四边形PMNQ为矩形.
∵点A在直线AC上,
∴当y=0时, x=8, 即A(8, 0).
设点 M 的运动时间为 m s, 则OM =m ,AN=3m.
∵点M , N在x轴上,
∴M(m, 0), N(8-3m, 0).
∵PM⊥x轴, QN⊥x轴,
∴∠PMA=∠QNA=90°.
∴PM∥QN.
∵点P在直线OC上, yoc=3x,
点Q在直线AC上,
∴P(m, 3m), Q(8-3m, 3m).
∴PM=QN.
∴四边形PMNQ为平行四边形.
又∵∠PMA=90°,
∴四边形PMNQ为矩形.
(2) ∵四边形PMNQ是正方形,
∴MN=QN, 即8-4m=|3m|, 解得 或8.
∴当点M 运动 或8s时,四边形PMNQ是正方形.
故答案为 或8.
8. 解: (1) ∵四边形ABCD是平行四边形,
∵在Rt△ABE中, ∠AEB=90°, ∠B=45°,
∴AE=3cm.
(2) ∵点M, N分别以A, C为起点, 1cm/s的速度沿AD, CB边运动,设点M , N运动的时间为 ts(0≤t≤6),
∴AM =CN =t.
∵AM∥CN,
∴四边形AMCN 为平行四边形.
∴当AN =AM 时, 四边形AMCN为菱形.
∵BE=AE=3, EN=6-t,
解得
故当 时, 四边形AMCN为菱形
(3)按照题干要求作图,如图57所示.
∵MP⊥BC于点P, NQ⊥AD于点Q,
∴四边形MPNQ为矩形.
∴当QM=QN时, 四边形MPNQ为正方形.
∵AM =CN=t, BE=3,
∴AQ=EN=BC-BE-CN=9-3-t=6-t.
(注:点Q在点M 的左侧或右侧).
∵QN=AE=3,
∴|2t-6|=3, 解得t=4.5或t=1.5.
故当t=4.5或t=1.5时, 四边形MPNQ为正方形.
23会当凌绝顶,一览众山小
9. 解: (1) ∵四边形ABCD是矩形,
∴AD∥BC.
∴∠CAD=∠ACB , ∠AEF=∠CFE.
∵EF 垂直平分AC,垂足为点O,
∴OA=OC.
∴△AOE≌△COF(AAS).
∴OE=OF.
∴四边形AFCE为平行四边形.
又∵EF⊥AC,
∴四边形AFCE为菱形.
设菱形的边长 , 则
∵在Rt△ABF中, AB=4cm,
解得x=5.
∴AF=5cm.
(2) ①当点P在AF上时, Q点在CD上, A, C, P, Q四点不构成平行四边形.
同理, 点P在AB上时, Q点在DE或CE上, A, C, P, Q四点不构成平行四边形.
点P在BF上,点Q在CD上时, A, C, P, Q四点不构成平行四边形.
只有当点P在BF上,点Q在ED上时,才能构成平行四边形.
综上所述,以A,C,P,Q四点为顶点的四边形是平行四边形时,
∵点P 的速度为5cm/s,点Q的速度为 运动时间为 ts,
∴5t=12-4t, 解得
∴以A, C, P, Q四点为顶点的四边形是平行四边形时,
② 由题意得,四边形APCQ是平行四边形时,点P,Q在互相平行的对应边上,有以下三种情况.
如图58所示,当点P在AF上,点Q在CE上时, 即a=12-b,得a+b=12.
如图59所示,当点P在BF上,点Q在DE上时,. 即12-b=a,得a+b=12.
如图60所示,当点P在AB上,点Q在CD上时, 即 得a+b=12.
综上所述,a与b满足的数量关系式是
