华师大版七下(2024版)第八章 三角形 小结与评价 课件
文档属性
| 名称 | 华师大版七下(2024版)第八章 三角形 小结与评价 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 14:18:01 | ||
图片预览










文档简介
(共32张PPT)
第八章 三角形
单元复习:小结与评价
01
教学目标
03
思考回顾
02
思维导图
04
典例精析
05
课堂巩固
06
作业布置
01
教学目标
1.复习三角形的基本性质(内角和、外角、三边关系)及分类。
2.掌握多边形内角和与外角和定理,能快速计算相关角度。
3.理解正多边形铺设地面的条件,能设计合理的铺设方案。
4.通过实际问题分析与几何建模,培养逻辑推理与空间想象能力。
02
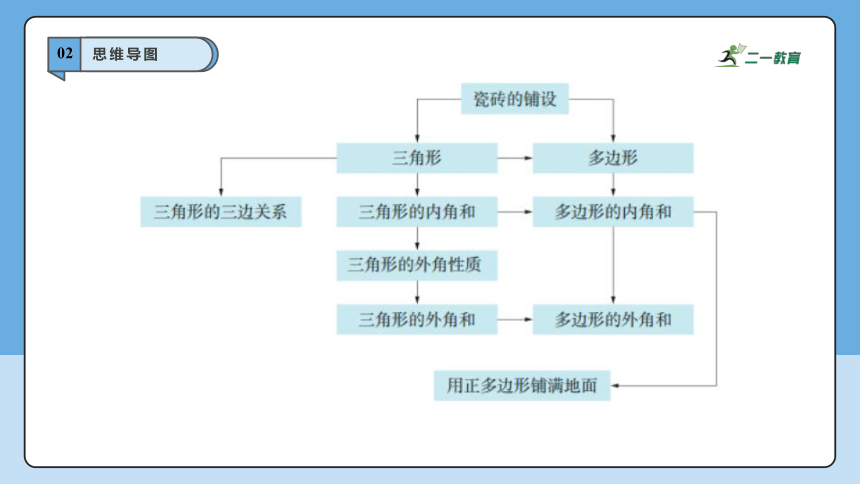
思维导图
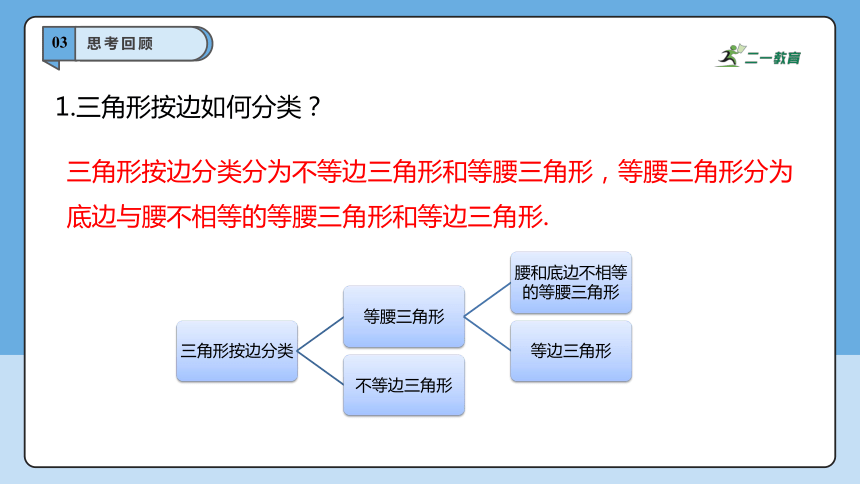
1.三角形按边如何分类?
三角形按边分类分为不等边三角形和等腰三角形,等腰三角形分为底边与腰不相等的等腰三角形和等边三角形.
03
思考回顾
2.三角形三边有什么关系?
任意两边之和大于第三边,任意两边之差小于第三边
03
思考回顾
高、中线、角平分线.每种都有三条,且所在直线都相交于一点.除了高线有可能在三角形的外部或边上外,中线和角平分线都在三角形的内部.
中线用来求线段长或等分面积,角平分线用来求角,高用来求面积.
3.三角形中三条重要线段指的是什么?它们有什么重要作用?
4.三角形的内角和定理是什么?三角形外角和是多少度?三角形外角的性质是什么?
三角形内角和等于180°;
三角形外角和为360°;
三角形的一个外角等于与它不相邻的两个内角的和.
03
思考回顾
(1)n边形的内角和等于(-2)×180°;
(2)多边形的外角和等于360°
5.多边形的内角和定理是什么?多边形的外角和是多少度?
03
知识回顾
围绕一点的角度和为360°(如正三角形:60°×6=360°)
6.用正多边形铺设地面的关键条件是什么?
1. 本章通过对三角形和多边形的一系列探索活动, 归纳得到关于三角形的边、 角及多边形的角的一些推断, 演绎证明了某些推断的正确性.
2. 推理的数学思想在本章得到了充分体现: 我们运用归纳推理, 从具体的多边形着手分析, 发现其中的逻辑关系, 归纳出多边形内角和公式; 我们还对探索得到的 “三角形的内角和等于 180°” 这一推断, 进行了演绎推理, 基本依据是有关平行线的一些基本事实和推导所得的结论.
3. 本章还将学习得到的数学结论用于实际生活, 理解某些正多边形能够铺满地面的道理.
03
思考回顾
例1如图,CD⊥AB于点D,已知∠ABC是钝角,则( )
A.线段CD是△ABC的AC边上的高线
B.线段CD是△ABC的AB边上的高线
C.线段AD是△ABC的BC边上的高线
D.线段AD是△ABC的AC边上的高线
04
典例精析
B
04
典例精析
例2如图,在中,的平分线相交于点,,则的度数是( )
A.118° B.119° C.120° D.121°
C
分析:利用三角形内角和定理,建立要求的角与已知角之间的关系解决问题
解:
的平分线分别为,
∴.
.答案:C
例3老师让同学们用20cm,90cm,100cm长的三根木条搭一个三角形,小明不小心把100cm的木条折断了,他用折断后剩下的较长木条与另两根木条怎么搭也不能搭成三角形.
(1)你知道这是为什么吗?
(2)小明把100cm的木条至少折去了多少厘米?
(3)如果100cm的木条折去了40cm,你能通过截90cm长的木条的办法帮小明搭一个小的三角形吗?
04
典例精析
分析:判断三条线段能否组成三角形,关键是看其是否满足三角形的三边关系.
04
典例精析
(2)设把的木条折去后,与另两根木条可搭成三角形。
根据题意得
解得.
小明把的木条至少折去了
(3)设的木条截去后,与另两根木条可以搭成一个小的三角形.
根据题意得(100-40)-20<90-a<(100-40)+20,解得10∴90cm的木条截去的长度应大于10cm且小于50cm才能搭成一个小的三角形.
分析:利用多边形的内角和公式和外角和建立方程解决.
04
典例精析
解:∵多边形外角和是360°,外角和是内角和的.
∴多边形的内角和为900°,
设多边形边数为n,则有(n-2)×180°=900,
解得n=7,
故答案选C.
C
例5已知等腰三角形ABC的两个底角相等(∠ABC=∠C),且一腰AC上的高BD与另一腰AB的夹角为40°.求∠ABC,∠C的度数.
解:(1)如图,BD在三角形的内部.
∵BD⊥AC,
∴∠ADB=90°.
∴∠A=180°-90°-40°=50°.
∴∠ABC=∠C=1/2(180°-∠A)=65°.
04
典例精析
分析:若等腰三角形的顶角是钝角,则腰上的高在三角形的外部;若等腰三角形的顶角是锐角,则腰上的高在三角形的内部,题中没明确指出三角形的形状,要分两种情况讨论.
解:(2)如图,BD在三角形的外部.
,
.
.
是的外角,
.
综上,的度数都是或都是.
04
典例精析
例6:如果用正方形材料和正n边形(n>4)材料能够把地面铺得既平整又无空隙,那么n的值为多少?
04
典例精析
分析:紧扣密铺的规则:围绕一点的几个内角的和等于360°,列出方程和不等式解决问题.
解:设正n边形内角的度数为x°
因为,所以.
设用块正方形,块正n边形拼,则有
(其中为正整数)
因为,所以,
即,故,所以或
.若,则,则x为270的因数
又因为,所以
,∴.
若,则,
则为的因数,而,故无解
综上,的值为8.
04
典例精析
方法点拨:用两种正多边形密铺,既要考虑两种正多边形每个内角的度数,又要考虑每种正多边形选用的块数,而密铺的规则是列方程的依据。
1.如图,BE是△ABC的高的是( )
2.从数学角度看下列四幅图片有一个与众不同,该图片是( )
05
课堂练习
【知识技能类作业】必做题:
C
C
04
课堂练习
【知识技能类作业】必做题:
3.一个多边形,它的内角和比外角和的4倍多180°,则这个多边形的边数是( )
A.9 B.10 C.11 D.12
C
04
课堂练习
【知识技能类作业】选做题:
C
A
4.如图,在△ABC中,∠C=60°,把△ABC沿直线DE折叠,使得点B与点A重合.若AD恰好平分∠BAC,则∠BDE的度数为( )
A.30° B.40° C.50° D.60°
5.如图,△ABC中,D、E、F分别是BC、AD、EC的中点,若S△ABD=4,则S△BFC=( )
A.2 B.1 C. D.
04
课堂练习
【综合拓展类作业】
解:(1)∵△BCD的周长为BC+CD+BD,△ACD的周长为AC+CD+AD,
∴△BCD与△ACD的周长差为BC-AC+BD-AD.
∵CD是△ABC的中线,
∴AD=BD.
又∵BC=3,AC=2,
∴BC-AC+BD-AD=BC-AC=3-2=1,即△BCD与△ACD的周长差为1.
6.如图,在△ABC中,BE是角平分线,点D在边AB上(不与点A,B重合),连结CD交BE于点O.
(1)若CD是中线,BC=3,AC=2,求△BCD与△ACD的周长差;
(2)若CD是高,∠ABC=62°,求∠BOC的度数.
04
课堂练习
【综合拓展类作业】
解(2)∵BE是∠ABC的平分线,∠ABC=62°,
∴∠ABE=∠ABC=×62°=31°.
∵CD是△ABC的高,
∴∠CDB=90°.
∴∠BOC=∠CDB+∠ABE=90°+31°=121°.
6.如图,在△ABC中,BE是角平分线,点D在边AB上(不与点A,B重合),连结CD交BE于点O.
(1)若CD是中线,BC=3,AC=2,求△BCD与△ACD的周长差;
(2)若CD是高,∠ABC=62°,求∠BOC的度数.
06
课堂小结
一、三角形基本性质
内角和:180°;外角性质:外角=不相邻两内角和
三边关系:a+b>c,a-b分类:按边(等边、等腰、不等边);按角(锐角、直角、钝角)
二、多边形定理
内角和:(n-2)×180°;外角和:360°
三、正多边形铺设
条件:围绕一点的角度和为360°(如正三角形:60°×6=360°)
1.如图,△ABC的角平分线AD,中线BE相交于点O,则下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.其中正确的结论是 .(填序号)
06
作业布置
【知识技能类作业】必做题:
①③
3.如图,在△ABC中,已知D、E、F分别为BC、AD、CE的中点.
(1)若S△ABC=1,则S△BEF= ;
(2)若S△BFC=1,则S△ABC= .
06
作业布置
【知识技能类作业】必做题:
100°
2.如图,在△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 .
4.已知a、b、c是△ABC的三边长.
(1)化简:|a-b+c|+|a-b-c|;
(2)若a和b满足方程组且c为偶数,求这个三角形的周长.
06
作业布置
【知识技能类作业】必做题:
解:∵两边之和大于第三边,两边之差小于第三边.
∴原式=a+c-b+b+c-a=2c
解:解方程组得,∴3∵c为偶数,∴c=4或6,
故a+b+c=2+5+4=11或a+b+c=2+5+6=13,
即三角形的周长为11或13.
5.如图,在△ABC中,∠A=60°,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,∠BDC=85°,则∠BDE的度数为 .
06
作业布置
【知识技能类作业】选做题:
25°
6.如图,在△ABC中,∠A=20°,CD是∠BCA的平分线,在△CDA中,DE是边CA上的高,如果∠EDA=∠CDB,求∠B的度数.
解:∵DE 是 CA 边上的高,
∴∠DEA=∠DEC=90°.∵∠A=20°,∴∠EDA=90°-20° =70°.
∵∠EDA= ∠CDB,∴∠CDE=180° -70°×2=40°.
在 Rt△CDE中,∠DCE=90°-40°=50°.
∵CD是∠BCA的平分线,∴∠BCA=2∠DCE=2×50°=100°.
∴∠B=180°-∠BCA-∠A=60°.
06
作业布置
【综合拓展类作业】
7.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为25°、75°、80°的三角形是“三倍角三角形”.
(1)△ABC中,∠A=20°,∠B=40°,△ABC是“三倍角三角形”吗?为什么?
(2)若△ABC是“三倍角三角形”,且∠B=30°,求△ABC中最大内角的度数.
解:(1)是,理由如下:
∵∠A=20°,∠B=40°,∴∠C=120°,
∵120=3×40,∴△ABC是“三倍角三角形”.
06
作业布置
【综合拓展类作业】
解: (2)∵ △ABC是“三倍角三角形”,且∠B=30°,
∴∠A+∠C=150°.
设△ABC的最大内角为x,
当最大内角是∠B的三倍时,即x=90°.
当最大内角是另一个角的三倍时,即x+3x=150°
∴x=37.5°,3x=112.5°
当∠B时∠A或∠C的三倍时, 则10°+30°+x=180°, ∴x=140°.
∴△ABC中最大内角的度数为90°或112.5°或140°
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第八章 三角形
单元复习:小结与评价
01
教学目标
03
思考回顾
02
思维导图
04
典例精析
05
课堂巩固
06
作业布置
01
教学目标
1.复习三角形的基本性质(内角和、外角、三边关系)及分类。
2.掌握多边形内角和与外角和定理,能快速计算相关角度。
3.理解正多边形铺设地面的条件,能设计合理的铺设方案。
4.通过实际问题分析与几何建模,培养逻辑推理与空间想象能力。
02
思维导图
1.三角形按边如何分类?
三角形按边分类分为不等边三角形和等腰三角形,等腰三角形分为底边与腰不相等的等腰三角形和等边三角形.
03
思考回顾
2.三角形三边有什么关系?
任意两边之和大于第三边,任意两边之差小于第三边
03
思考回顾
高、中线、角平分线.每种都有三条,且所在直线都相交于一点.除了高线有可能在三角形的外部或边上外,中线和角平分线都在三角形的内部.
中线用来求线段长或等分面积,角平分线用来求角,高用来求面积.
3.三角形中三条重要线段指的是什么?它们有什么重要作用?
4.三角形的内角和定理是什么?三角形外角和是多少度?三角形外角的性质是什么?
三角形内角和等于180°;
三角形外角和为360°;
三角形的一个外角等于与它不相邻的两个内角的和.
03
思考回顾
(1)n边形的内角和等于(-2)×180°;
(2)多边形的外角和等于360°
5.多边形的内角和定理是什么?多边形的外角和是多少度?
03
知识回顾
围绕一点的角度和为360°(如正三角形:60°×6=360°)
6.用正多边形铺设地面的关键条件是什么?
1. 本章通过对三角形和多边形的一系列探索活动, 归纳得到关于三角形的边、 角及多边形的角的一些推断, 演绎证明了某些推断的正确性.
2. 推理的数学思想在本章得到了充分体现: 我们运用归纳推理, 从具体的多边形着手分析, 发现其中的逻辑关系, 归纳出多边形内角和公式; 我们还对探索得到的 “三角形的内角和等于 180°” 这一推断, 进行了演绎推理, 基本依据是有关平行线的一些基本事实和推导所得的结论.
3. 本章还将学习得到的数学结论用于实际生活, 理解某些正多边形能够铺满地面的道理.
03
思考回顾
例1如图,CD⊥AB于点D,已知∠ABC是钝角,则( )
A.线段CD是△ABC的AC边上的高线
B.线段CD是△ABC的AB边上的高线
C.线段AD是△ABC的BC边上的高线
D.线段AD是△ABC的AC边上的高线
04
典例精析
B
04
典例精析
例2如图,在中,的平分线相交于点,,则的度数是( )
A.118° B.119° C.120° D.121°
C
分析:利用三角形内角和定理,建立要求的角与已知角之间的关系解决问题
解:
的平分线分别为,
∴.
.答案:C
例3老师让同学们用20cm,90cm,100cm长的三根木条搭一个三角形,小明不小心把100cm的木条折断了,他用折断后剩下的较长木条与另两根木条怎么搭也不能搭成三角形.
(1)你知道这是为什么吗?
(2)小明把100cm的木条至少折去了多少厘米?
(3)如果100cm的木条折去了40cm,你能通过截90cm长的木条的办法帮小明搭一个小的三角形吗?
04
典例精析
分析:判断三条线段能否组成三角形,关键是看其是否满足三角形的三边关系.
04
典例精析
(2)设把的木条折去后,与另两根木条可搭成三角形。
根据题意得
解得.
小明把的木条至少折去了
(3)设的木条截去后,与另两根木条可以搭成一个小的三角形.
根据题意得(100-40)-20<90-a<(100-40)+20,解得10
分析:利用多边形的内角和公式和外角和建立方程解决.
04
典例精析
解:∵多边形外角和是360°,外角和是内角和的.
∴多边形的内角和为900°,
设多边形边数为n,则有(n-2)×180°=900,
解得n=7,
故答案选C.
C
例5已知等腰三角形ABC的两个底角相等(∠ABC=∠C),且一腰AC上的高BD与另一腰AB的夹角为40°.求∠ABC,∠C的度数.
解:(1)如图,BD在三角形的内部.
∵BD⊥AC,
∴∠ADB=90°.
∴∠A=180°-90°-40°=50°.
∴∠ABC=∠C=1/2(180°-∠A)=65°.
04
典例精析
分析:若等腰三角形的顶角是钝角,则腰上的高在三角形的外部;若等腰三角形的顶角是锐角,则腰上的高在三角形的内部,题中没明确指出三角形的形状,要分两种情况讨论.
解:(2)如图,BD在三角形的外部.
,
.
.
是的外角,
.
综上,的度数都是或都是.
04
典例精析
例6:如果用正方形材料和正n边形(n>4)材料能够把地面铺得既平整又无空隙,那么n的值为多少?
04
典例精析
分析:紧扣密铺的规则:围绕一点的几个内角的和等于360°,列出方程和不等式解决问题.
解:设正n边形内角的度数为x°
因为,所以.
设用块正方形,块正n边形拼,则有
(其中为正整数)
因为,所以,
即,故,所以或
.若,则,则x为270的因数
又因为,所以
,∴.
若,则,
则为的因数,而,故无解
综上,的值为8.
04
典例精析
方法点拨:用两种正多边形密铺,既要考虑两种正多边形每个内角的度数,又要考虑每种正多边形选用的块数,而密铺的规则是列方程的依据。
1.如图,BE是△ABC的高的是( )
2.从数学角度看下列四幅图片有一个与众不同,该图片是( )
05
课堂练习
【知识技能类作业】必做题:
C
C
04
课堂练习
【知识技能类作业】必做题:
3.一个多边形,它的内角和比外角和的4倍多180°,则这个多边形的边数是( )
A.9 B.10 C.11 D.12
C
04
课堂练习
【知识技能类作业】选做题:
C
A
4.如图,在△ABC中,∠C=60°,把△ABC沿直线DE折叠,使得点B与点A重合.若AD恰好平分∠BAC,则∠BDE的度数为( )
A.30° B.40° C.50° D.60°
5.如图,△ABC中,D、E、F分别是BC、AD、EC的中点,若S△ABD=4,则S△BFC=( )
A.2 B.1 C. D.
04
课堂练习
【综合拓展类作业】
解:(1)∵△BCD的周长为BC+CD+BD,△ACD的周长为AC+CD+AD,
∴△BCD与△ACD的周长差为BC-AC+BD-AD.
∵CD是△ABC的中线,
∴AD=BD.
又∵BC=3,AC=2,
∴BC-AC+BD-AD=BC-AC=3-2=1,即△BCD与△ACD的周长差为1.
6.如图,在△ABC中,BE是角平分线,点D在边AB上(不与点A,B重合),连结CD交BE于点O.
(1)若CD是中线,BC=3,AC=2,求△BCD与△ACD的周长差;
(2)若CD是高,∠ABC=62°,求∠BOC的度数.
04
课堂练习
【综合拓展类作业】
解(2)∵BE是∠ABC的平分线,∠ABC=62°,
∴∠ABE=∠ABC=×62°=31°.
∵CD是△ABC的高,
∴∠CDB=90°.
∴∠BOC=∠CDB+∠ABE=90°+31°=121°.
6.如图,在△ABC中,BE是角平分线,点D在边AB上(不与点A,B重合),连结CD交BE于点O.
(1)若CD是中线,BC=3,AC=2,求△BCD与△ACD的周长差;
(2)若CD是高,∠ABC=62°,求∠BOC的度数.
06
课堂小结
一、三角形基本性质
内角和:180°;外角性质:外角=不相邻两内角和
三边关系:a+b>c,a-b
二、多边形定理
内角和:(n-2)×180°;外角和:360°
三、正多边形铺设
条件:围绕一点的角度和为360°(如正三角形:60°×6=360°)
1.如图,△ABC的角平分线AD,中线BE相交于点O,则下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.其中正确的结论是 .(填序号)
06
作业布置
【知识技能类作业】必做题:
①③
3.如图,在△ABC中,已知D、E、F分别为BC、AD、CE的中点.
(1)若S△ABC=1,则S△BEF= ;
(2)若S△BFC=1,则S△ABC= .
06
作业布置
【知识技能类作业】必做题:
100°
2.如图,在△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 .
4.已知a、b、c是△ABC的三边长.
(1)化简:|a-b+c|+|a-b-c|;
(2)若a和b满足方程组且c为偶数,求这个三角形的周长.
06
作业布置
【知识技能类作业】必做题:
解:∵两边之和大于第三边,两边之差小于第三边.
∴原式=a+c-b+b+c-a=2c
解:解方程组得,∴3
故a+b+c=2+5+4=11或a+b+c=2+5+6=13,
即三角形的周长为11或13.
5.如图,在△ABC中,∠A=60°,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,∠BDC=85°,则∠BDE的度数为 .
06
作业布置
【知识技能类作业】选做题:
25°
6.如图,在△ABC中,∠A=20°,CD是∠BCA的平分线,在△CDA中,DE是边CA上的高,如果∠EDA=∠CDB,求∠B的度数.
解:∵DE 是 CA 边上的高,
∴∠DEA=∠DEC=90°.∵∠A=20°,∴∠EDA=90°-20° =70°.
∵∠EDA= ∠CDB,∴∠CDE=180° -70°×2=40°.
在 Rt△CDE中,∠DCE=90°-40°=50°.
∵CD是∠BCA的平分线,∴∠BCA=2∠DCE=2×50°=100°.
∴∠B=180°-∠BCA-∠A=60°.
06
作业布置
【综合拓展类作业】
7.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为25°、75°、80°的三角形是“三倍角三角形”.
(1)△ABC中,∠A=20°,∠B=40°,△ABC是“三倍角三角形”吗?为什么?
(2)若△ABC是“三倍角三角形”,且∠B=30°,求△ABC中最大内角的度数.
解:(1)是,理由如下:
∵∠A=20°,∠B=40°,∴∠C=120°,
∵120=3×40,∴△ABC是“三倍角三角形”.
06
作业布置
【综合拓展类作业】
解: (2)∵ △ABC是“三倍角三角形”,且∠B=30°,
∴∠A+∠C=150°.
设△ABC的最大内角为x,
当最大内角是∠B的三倍时,即x=90°.
当最大内角是另一个角的三倍时,即x+3x=150°
∴x=37.5°,3x=112.5°
当∠B时∠A或∠C的三倍时, 则10°+30°+x=180°, ∴x=140°.
∴△ABC中最大内角的度数为90°或112.5°或140°
Thanks!
https://www.21cnjy.com/recruitment/home/fine
