华师大版七下(2024版)三角形单元小结与评价课时教案
文档属性
| 名称 | 华师大版七下(2024版)三角形单元小结与评价课时教案 |  | |
| 格式 | docx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 14:18:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
分课时教学设计
第9课时《三角形单元小结与评价》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 本章系统梳理了三角形的基本概念、分类、内角与外角性质、三角形的三边关系、多边形的内角和与外角和定理,以及正多边形铺设地面的应用。通过复习,帮助学生巩固几何基础,强化逻辑推理能力,提升解决实际问题的综合素养。
学习者分析 学生已掌握三角形的基本性质,但对多边形内角和公式的灵活应用存在不足,正多边形铺设地面的实际问题中易忽略角度匹配条件。部分学生在复杂图形分析中缺乏空间想象力,需通过针对性训练加强。
教学目标 1.复习三角形的基本性质(内角和、外角、三边关系)及分类。 2.掌握多边形内角和与外角和定理,能快速计算相关角度。 3.理解正多边形铺设地面的条件,能设计合理的铺设方案。 4.通过实际问题分析与几何建模,培养逻辑推理与空间想象能力。
教学重点 1.三角形内角和定理与三边关系的应用。 2.多边形内角和公式的推导与计算。 3.正多边形平面镶嵌的条件分析。
教学难点 1.复杂图形中多角度关系的综合运用。 2.正多边形组合铺设地面的角度匹配逻辑。
学习活动设计
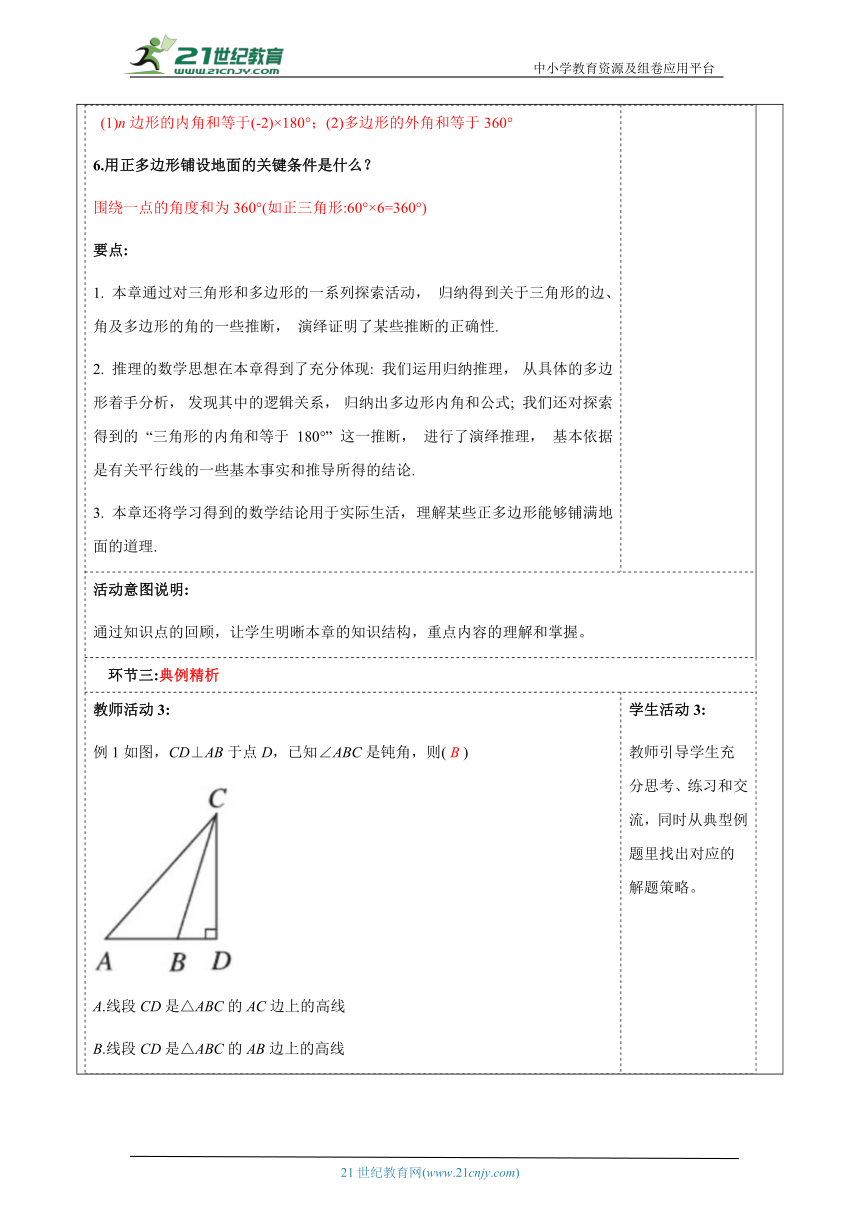
教师活动学生活动环节一:构建知识体系教师活动1: 知识结构图 学生活动1: 给学生充分的时间把课本知识简单复习,然后梳理总结形成本章的知识结构框架。 活动意图说明: 在知识体系的指导下,我们可以更有针对性地进行学习。当我们需要掌握某个领域的知识时,可以清晰地了解需要学习的内容和顺序,避免盲目学习造成的时间和精力浪费。环节二: 思考回顾教师活动2: 1.三角形按边如何分类? 三角形按边分类分为不等边三角形和等腰三角形,等腰三角形分为底边与腰不相等的等腰三角形和等边三角形. 2.三角形三边有什么关系? 任意两边之和大于第三边,任意两边之差小于第三边 3.三角形中三条重要线段指的是什么?它们有什么重要作用? 高、中线、角平分线.每种都有三条,且所在直线都相交于一点.除了高线有可能在三角形的外部或边上外,中线和角平分线都在三角形的内部. 中线用来求线段长或等分面积,角平分线用来求角,高用来求面积. 4.三角形的内角和定理是什么?三角形外角和是多少度?三角形外角的性质是什么? 三角形内角和等于180°;三角形外角和为360°;三角形的一个外角等于与它不相邻的两个内角的和. 5.多边形的内角和定理是什么?多边形的外角和是多少度? (1)n边形的内角和等于(-2)×180°;(2)多边形的外角和等于360° 6.用正多边形铺设地面的关键条件是什么? 围绕一点的角度和为360°(如正三角形:60°×6=360°) 要点: 1. 本章通过对三角形和多边形的一系列探索活动, 归纳得到关于三角形的边、 角及多边形的角的一些推断, 演绎证明了某些推断的正确性. 2. 推理的数学思想在本章得到了充分体现: 我们运用归纳推理, 从具体的多边形着手分析, 发现其中的逻辑关系, 归纳出多边形内角和公式; 我们还对探索得到的 “三角形的内角和等于 180°” 这一推断, 进行了演绎推理, 基本依据是有关平行线的一些基本事实和推导所得的结论. 3. 本章还将学习得到的数学结论用于实际生活, 理解某些正多边形能够铺满地面的道理.学生活动2: 学生回顾本章知识点,学生思考回答.活动意图说明: 通过知识点的回顾,让学生明晰本章的知识结构,重点内容的理解和掌握。环节三:典例精析教师活动3: 例1如图,CD⊥AB于点D,已知∠ABC是钝角,则( B ) A.线段CD是△ABC的AC边上的高线 B.线段CD是△ABC的AB边上的高线 C.线段AD是△ABC的BC边上的高线 D.线段AD是△ABC的AC边上的高线 例2如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数是( ) A.118° B.119° C.120° D.121° 分析:利用三角形内角和定理,建立要求的角与已知角之间的关系解决问题 解:∵∠A=60°,∠ABC=42°, ∴.∠ACB=180°-∠A-∠ABC=78°. ∵∠ABC,∠ACB的平分线分别为BE,CD, ∴. ∴∠BFC=180°-∠FBC-∠FCB=120° 答案:C 方法点拨:运用三角形内角和定理求角的度数时,先找出所求角所在的三角形,然后结合已知条件分析要求的角与已知角之间的关系. 例3老师让同学们用20cm,90cm,100cm长的三根木条搭一个三角形,小明不小心把100cm的木条折断了,他用折断后剩下的较长木条与另两根木条怎么搭也不能搭成三角形. (1)你知道这是为什么吗? (2)小明把100cm的木条至少折去了多少厘米? (3)如果100cm的木条折去了40cm,你能通过截90cm长的木条的办法帮小明搭一个小的三角形吗? 分析:判断三条线段能否组成三角形,关键是看其是否满足三角形的三边关系 解:(1)构成三角形的三条线段必须满足任意两条线段之和大于第三条线段,任意两条线段之差小于第三条线段.小明不能搭成三角形的原因是所用的木条与的两根木条不符合该条件。 (2)设把的木条折去后,与另两根木条可搭成三角形。 根据题意得 解得. 小明把的木条至少折去了 (3)设的木条截去后,与另两根木条可以搭成一个小的三角形. 根据题意得(100-40)-20<90-a<(100-40)+20,解得104)材料能够把地面铺得既平整又无空隙,那么n的值为多少? 分析:紧扣密铺的规则:围绕一点的几个内角的和等于360°,列出方程和不等式解决问题. 解:设正n边形内角的度数为x° 因为,所以. 设用块正方形,块正n边形拼,则有 (其中为正整数) 因为,所以, 即,故,所以或 若,则,则x为270的因数 又因为,所以 ,∴. 若,则, 则为的因数,而,故无解 综上,的值为8. 方法点拨:用两种正多边形密铺,既要考虑两种正多边形每个内角的度数,又要考虑每种正多边形选用的块数,而密铺的规则是列方程的依据。学生活动3: 教师引导学生充分思考、练习和交流,同时从典型例题里找出对应的解题策略。活动意图说明: 通过知识点的回顾与例题的学习,让学生理解三角形的内角和与外角的性质、多边形的内角和与外角和,正多边形铺设地面。提高解决实际问题的能力,使学生对本章知识内容有进一步的理解和掌握.培养学生积极思考,合作交流的习惯。
板书设计 第8章小结与评价 一、三角形基本性质 内角和:180°;外角性质:外角=不相邻两内角和 三边关系:a+b>c,a-b课堂练习 【知识技能类作业】 必做题: 1.如图,BE是△ABC的高的是( ) 2.从数学角度看下列四幅图片有一个与众不同,该图片是( ) 3.一个多边形,它的内角和比外角和的4倍多180°,则这个多边形的边数是( ) A.9 B.10 C.11 D.12 选做题: 4.如图,在△ABC中,∠C=60°,把△ABC沿直线DE折叠,使得点B与点A重合.若AD恰好平分∠BAC,则∠BDE的度数为( ) A.30° B.40° C.50° D.60° 5.如图,△ABC中,D、E、F分别是BC、AD、EC的中点,若S△ABD=4,则S△BFC=( ) A.2 B.1 C. D. 6.如图,在△ABC中,BE是角平分线,点D在边AB上(不与点A,B重合),连结CD交BE于点O. (1)若CD是中线,BC=3,AC=2,求△BCD与△ACD的周长差; (2)若CD是高,∠ABC=62°,求∠BOC的度数. 【综合拓展类作业】 7.阅读小明和小红的对话,解决下列问题. (1)这个“多加的锐角”是________°. (2)若这是个正多边形,则这个正多边形的一个内角是多少度? 1.C 解析:A.BE不是△ABC的高,不符合题意;B.BE不是△ABC的高,不符合题意;C.BE是△ABC的高,符合题意;D.BE不是△ABC的高,不符合题意.故选C. 2.C 解析:∵C选项中的伸缩门是利用了四边形的不稳定性,A、B、D选项都是利用了三角形的稳定性,∴选项C中的图片与众不同.故选C. 3.C 解析:设这个多边形的边数为n,根据题意,得 (n-2)·180°=360°×4+180°, 解得n=11.则这个多边形的边数是11.故选C. 4.C 解析:由折叠可知∠B=∠DAB,∠BED=∠AED=90°. ∵AD平分∠BAC, ∴∠BAD=∠CAD. ∵∠B+∠BAC+∠C=180°,∠C=60°,∴3∠B=120°.解得∠B=40°.∴∠BDE=90°-40°=50°.故选C. 5.A 解析:如图,连结BE, ∵点D、E、F分别是BC、AD、EC的中点, ∴AE=DE=AD,EF=CF=CE,BD=DC=BC. ∵S△ABD=4, ∴S△ABD=S△ACD=4, S△ABE=S△BED=S△ABD=2,S△AEC=S△CDE=S△ACD=2. ∴S△BEC=S△BDE+S△CDE=2+2=4. ∴S△BFC=S△BEF=S△BEC=×4=2.故选A. 6.解:(1)∵△BCD的周长为BC+CD+BD,△ACD的周长为AC+CD+AD, ∴△BCD与△ACD的周长差为BC-AC+BD-AD. ∵CD是△ABC的中线, ∴AD=BD. 又∵BC=3,AC=2, ∴BC-AC+BD-AD=BC-AC=3-2=1,即△BCD与△ACD的周长差为1. (2)∵BE是∠ABC的平分线,∠ABC=62°, ∴∠ABE=∠ABC=×62°=31°. ∵CD是△ABC的高, ∴∠CDB=90°. ∴∠BOC=∠CDB+∠ABE=90°+31°=121°. 7.解:(1)30 (2)由(1)知,这个多边形是正十二边形, 所以这个正多边形的一个内角是180°-=150°.
作业设计 【知识技能类作业】 必做题: 1.如图,△ABC的角平分线AD,中线BE相交于点O,则下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.其中正确的结论是 .(填序号) 第1题图 2.如图,在△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 . 第2题图 3.如图,在△ABC中,已知D、E、F分别为BC、AD、CE的中点. (1)若S△ABC=1,则S△BEF= ; (2)若S△BFC=1,则S△ABC= . 4.已知a、b、c是△ABC的三边长. (1)化简:|a-b+c|+|a-b-c|; (2)若a和b满足方程组且c为偶数,求这个三角形的周长. 选做题: 5.如图,在△ABC中,∠A=60°,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,∠BDC=85°,则∠BDE的度数为 . 6.如图,在△ABC中,∠A=20°,CD是∠BCA的平分线,在△CDA中,DE是边CA上的高,如果∠EDA=∠CDB,求∠B的度数. 【综合拓展类作业】 7.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为25°、75°、80°的三角形是“三倍角三角形”. (1)△ABC中,∠A=20°,∠B=40°,△ABC是“三倍角三角形”吗?为什么? (2)若△ABC是“三倍角三角形”,且∠B=30°,求△ABC中最大内角的度数. 1.①③ 2.100° 3.(1) (2)4 4.(1)2c (2)这个三角形的周长为11或13. 5.25° 6. 解:∵DE 是 CA 边上的高, ∴∠DEA=∠DEC=90°.∵∠A=20°,∴∠EDA=90°-20° =70°. ∵∠EDA= ∠CDB,∴∠CDE=180° -70°×2=40°. 在 Rt△CDE中,∠DCE=90°-40°=50°. ∵CD是∠BCA的平分线,∴∠BCA=2∠DCE=2×50°=100°. ∴∠B=180°-∠BCA-∠A=60°. 7. 解:(1)是,理由如下: ∵∠A=20°,∠B=40°,∴∠C=120°, ∵120=3×40,∴△ABC是“三倍角三角形”. (2)∵ △ABC是“三倍角三角形”,且∠B=30°, ∴∠A+∠C=150°. 设△ABC的最大内角为x, 当最大内角是∠B的三倍时,即x=90°. 当最大内角是另一个角的三倍时,即x+3x=150° ∴x=37.5°,3x=112.5° 当∠B是∠A或∠C的三倍时, 则10°+30°+x=180°, ∴x=140°. ∴△ABC中最大内角的度数为90°或112.5°或140°
教学反思 本次复习课以三角形与多边形为核心,通过例题解析与实际应用结合,强化了几何推理能力。多数学生能熟练应用内角和公式,但在正多边形组合铺设的抽象分析中表现不足。未来可引入动态几何工具(如GeoGebra),直观展示图形拼接过程,帮助学生理解角度匹配原理。
21世纪教育网(www.21cnjy.com)
分课时教学设计
第9课时《三角形单元小结与评价》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 本章系统梳理了三角形的基本概念、分类、内角与外角性质、三角形的三边关系、多边形的内角和与外角和定理,以及正多边形铺设地面的应用。通过复习,帮助学生巩固几何基础,强化逻辑推理能力,提升解决实际问题的综合素养。
学习者分析 学生已掌握三角形的基本性质,但对多边形内角和公式的灵活应用存在不足,正多边形铺设地面的实际问题中易忽略角度匹配条件。部分学生在复杂图形分析中缺乏空间想象力,需通过针对性训练加强。
教学目标 1.复习三角形的基本性质(内角和、外角、三边关系)及分类。 2.掌握多边形内角和与外角和定理,能快速计算相关角度。 3.理解正多边形铺设地面的条件,能设计合理的铺设方案。 4.通过实际问题分析与几何建模,培养逻辑推理与空间想象能力。
教学重点 1.三角形内角和定理与三边关系的应用。 2.多边形内角和公式的推导与计算。 3.正多边形平面镶嵌的条件分析。
教学难点 1.复杂图形中多角度关系的综合运用。 2.正多边形组合铺设地面的角度匹配逻辑。
学习活动设计
教师活动学生活动环节一:构建知识体系教师活动1: 知识结构图 学生活动1: 给学生充分的时间把课本知识简单复习,然后梳理总结形成本章的知识结构框架。 活动意图说明: 在知识体系的指导下,我们可以更有针对性地进行学习。当我们需要掌握某个领域的知识时,可以清晰地了解需要学习的内容和顺序,避免盲目学习造成的时间和精力浪费。环节二: 思考回顾教师活动2: 1.三角形按边如何分类? 三角形按边分类分为不等边三角形和等腰三角形,等腰三角形分为底边与腰不相等的等腰三角形和等边三角形. 2.三角形三边有什么关系? 任意两边之和大于第三边,任意两边之差小于第三边 3.三角形中三条重要线段指的是什么?它们有什么重要作用? 高、中线、角平分线.每种都有三条,且所在直线都相交于一点.除了高线有可能在三角形的外部或边上外,中线和角平分线都在三角形的内部. 中线用来求线段长或等分面积,角平分线用来求角,高用来求面积. 4.三角形的内角和定理是什么?三角形外角和是多少度?三角形外角的性质是什么? 三角形内角和等于180°;三角形外角和为360°;三角形的一个外角等于与它不相邻的两个内角的和. 5.多边形的内角和定理是什么?多边形的外角和是多少度? (1)n边形的内角和等于(-2)×180°;(2)多边形的外角和等于360° 6.用正多边形铺设地面的关键条件是什么? 围绕一点的角度和为360°(如正三角形:60°×6=360°) 要点: 1. 本章通过对三角形和多边形的一系列探索活动, 归纳得到关于三角形的边、 角及多边形的角的一些推断, 演绎证明了某些推断的正确性. 2. 推理的数学思想在本章得到了充分体现: 我们运用归纳推理, 从具体的多边形着手分析, 发现其中的逻辑关系, 归纳出多边形内角和公式; 我们还对探索得到的 “三角形的内角和等于 180°” 这一推断, 进行了演绎推理, 基本依据是有关平行线的一些基本事实和推导所得的结论. 3. 本章还将学习得到的数学结论用于实际生活, 理解某些正多边形能够铺满地面的道理.学生活动2: 学生回顾本章知识点,学生思考回答.活动意图说明: 通过知识点的回顾,让学生明晰本章的知识结构,重点内容的理解和掌握。环节三:典例精析教师活动3: 例1如图,CD⊥AB于点D,已知∠ABC是钝角,则( B ) A.线段CD是△ABC的AC边上的高线 B.线段CD是△ABC的AB边上的高线 C.线段AD是△ABC的BC边上的高线 D.线段AD是△ABC的AC边上的高线 例2如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数是( ) A.118° B.119° C.120° D.121° 分析:利用三角形内角和定理,建立要求的角与已知角之间的关系解决问题 解:∵∠A=60°,∠ABC=42°, ∴.∠ACB=180°-∠A-∠ABC=78°. ∵∠ABC,∠ACB的平分线分别为BE,CD, ∴. ∴∠BFC=180°-∠FBC-∠FCB=120° 答案:C 方法点拨:运用三角形内角和定理求角的度数时,先找出所求角所在的三角形,然后结合已知条件分析要求的角与已知角之间的关系. 例3老师让同学们用20cm,90cm,100cm长的三根木条搭一个三角形,小明不小心把100cm的木条折断了,他用折断后剩下的较长木条与另两根木条怎么搭也不能搭成三角形. (1)你知道这是为什么吗? (2)小明把100cm的木条至少折去了多少厘米? (3)如果100cm的木条折去了40cm,你能通过截90cm长的木条的办法帮小明搭一个小的三角形吗? 分析:判断三条线段能否组成三角形,关键是看其是否满足三角形的三边关系 解:(1)构成三角形的三条线段必须满足任意两条线段之和大于第三条线段,任意两条线段之差小于第三条线段.小明不能搭成三角形的原因是所用的木条与的两根木条不符合该条件。 (2)设把的木条折去后,与另两根木条可搭成三角形。 根据题意得 解得. 小明把的木条至少折去了 (3)设的木条截去后,与另两根木条可以搭成一个小的三角形. 根据题意得(100-40)-20<90-a<(100-40)+20,解得10
板书设计 第8章小结与评价 一、三角形基本性质 内角和:180°;外角性质:外角=不相邻两内角和 三边关系:a+b>c,a-b
作业设计 【知识技能类作业】 必做题: 1.如图,△ABC的角平分线AD,中线BE相交于点O,则下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.其中正确的结论是 .(填序号) 第1题图 2.如图,在△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 . 第2题图 3.如图,在△ABC中,已知D、E、F分别为BC、AD、CE的中点. (1)若S△ABC=1,则S△BEF= ; (2)若S△BFC=1,则S△ABC= . 4.已知a、b、c是△ABC的三边长. (1)化简:|a-b+c|+|a-b-c|; (2)若a和b满足方程组且c为偶数,求这个三角形的周长. 选做题: 5.如图,在△ABC中,∠A=60°,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,∠BDC=85°,则∠BDE的度数为 . 6.如图,在△ABC中,∠A=20°,CD是∠BCA的平分线,在△CDA中,DE是边CA上的高,如果∠EDA=∠CDB,求∠B的度数. 【综合拓展类作业】 7.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为25°、75°、80°的三角形是“三倍角三角形”. (1)△ABC中,∠A=20°,∠B=40°,△ABC是“三倍角三角形”吗?为什么? (2)若△ABC是“三倍角三角形”,且∠B=30°,求△ABC中最大内角的度数. 1.①③ 2.100° 3.(1) (2)4 4.(1)2c (2)这个三角形的周长为11或13. 5.25° 6. 解:∵DE 是 CA 边上的高, ∴∠DEA=∠DEC=90°.∵∠A=20°,∴∠EDA=90°-20° =70°. ∵∠EDA= ∠CDB,∴∠CDE=180° -70°×2=40°. 在 Rt△CDE中,∠DCE=90°-40°=50°. ∵CD是∠BCA的平分线,∴∠BCA=2∠DCE=2×50°=100°. ∴∠B=180°-∠BCA-∠A=60°. 7. 解:(1)是,理由如下: ∵∠A=20°,∠B=40°,∴∠C=120°, ∵120=3×40,∴△ABC是“三倍角三角形”. (2)∵ △ABC是“三倍角三角形”,且∠B=30°, ∴∠A+∠C=150°. 设△ABC的最大内角为x, 当最大内角是∠B的三倍时,即x=90°. 当最大内角是另一个角的三倍时,即x+3x=150° ∴x=37.5°,3x=112.5° 当∠B是∠A或∠C的三倍时, 则10°+30°+x=180°, ∴x=140°. ∴△ABC中最大内角的度数为90°或112.5°或140°
教学反思 本次复习课以三角形与多边形为核心,通过例题解析与实际应用结合,强化了几何推理能力。多数学生能熟练应用内角和公式,但在正多边形组合铺设的抽象分析中表现不足。未来可引入动态几何工具(如GeoGebra),直观展示图形拼接过程,帮助学生理解角度匹配原理。
21世纪教育网(www.21cnjy.com)
