6.4 探索三角形相似的条件 练习(5课时、含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 6.4 探索三角形相似的条件 练习(5课时、含答案) 2024-2025学年数学苏科版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 222.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览

文档简介
6.4 探索三角形相似的条件
第1课时 平行线分线段成比例及平行线截三角形相似
1. 两条直线被一组平行线所截,所得的对应线段 .
2. 平行于三角形一边的直线与其他两边相交,所截得的三角形与原三角形 .
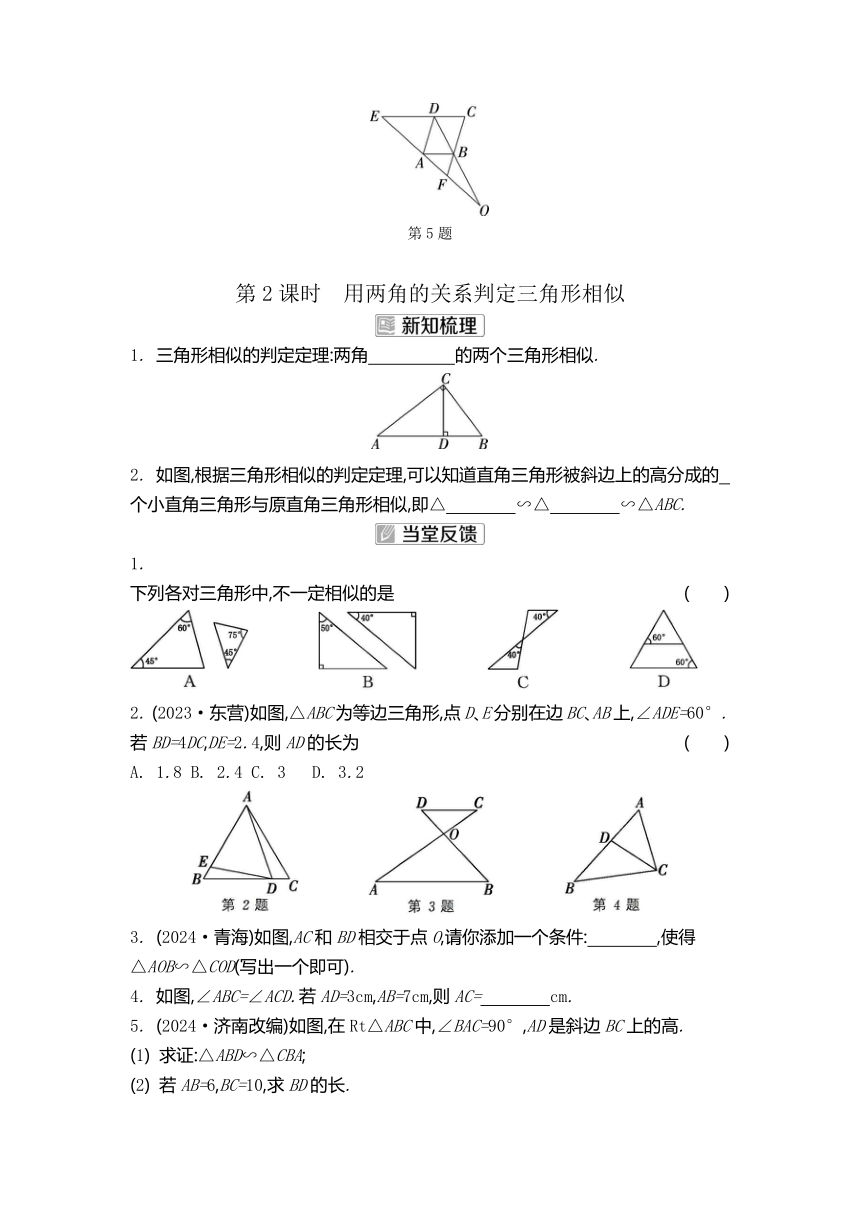
1. (2023·吉林)如图,在△ABC中,点D在边AB上,过点D作DE∥BC,交AC于点E.若AD=2,BD=3,则的值是 ( )
A. B. C. D.
2. (2024·湖南改编)如图,在△ABC中,D、E分别为边AB、AC的中点.下列结论错误的是 ( )
A. △ADE∽△ABC B. △ADE与△ABC的相似比是2
C. DE∶BC=1∶2 D. ∠AED=∠C
3. 如图,直线l1∥l2∥l3,另有两条直线分别交l1、l2、l3于点A、B、C及点D、E、F,且AB=3,DE=6,EF=2,则BC的长为 .
4. (2024·河南)如图,在 ABCD中,对角线AC、BD相交于点O,E为OC的中点,EF∥AB,交BC于点F.若AB=4,则EF的长为 .
5. 如图,EC∥AB,∠EDA=∠ABF.指出图中所有的相似三角形(不含相似比为1的相似三角形).
第5题
第2课时 用两角的关系判定三角形相似
1. 三角形相似的判定定理:两角 的两个三角形相似.
2. 如图,根据三角形相似的判定定理,可以知道直角三角形被斜边上的高分成的 个小直角三角形与原直角三角形相似,即△ ∽△ ∽△ABC.
1.
下列各对三角形中,不一定相似的是 ( )
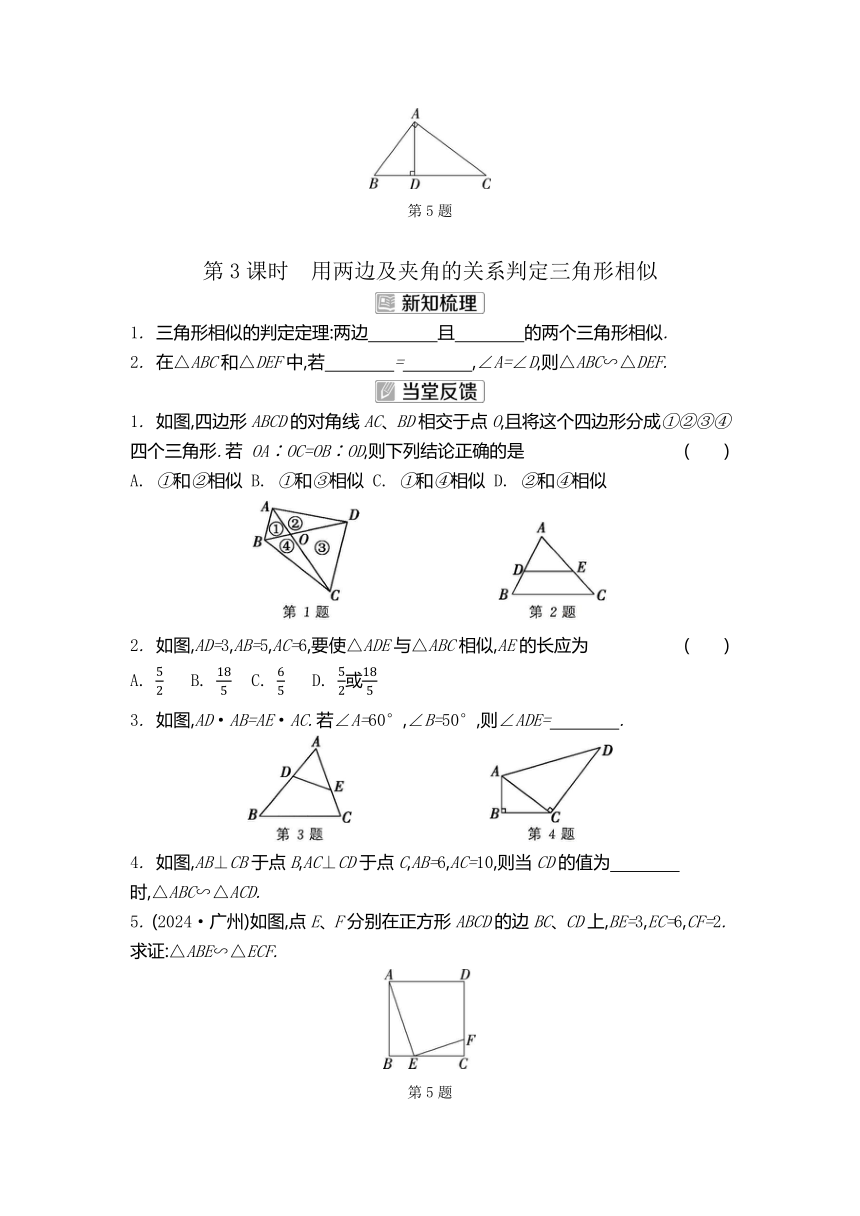
2. (2023·东营)如图,△ABC为等边三角形,点D、E分别在边BC、AB上,∠ADE=60°.若BD=4DC,DE=2.4,则AD的长为 ( )
A. 1.8 B. 2.4 C. 3 D. 3.2
3. (2024·青海)如图,AC和BD相交于点O,请你添加一个条件: ,使得△AOB∽△COD(写出一个即可).
4. 如图,∠ABC=∠ACD.若AD=3cm,AB=7cm,则AC= cm.
5. (2024·济南改编)如图,在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1) 求证:△ABD∽△CBA;
(2) 若AB=6,BC=10,求BD的长.
第5题
第3课时 用两边及夹角的关系判定三角形相似
1. 三角形相似的判定定理:两边 且 的两个三角形相似.
2. 在△ABC和△DEF中,若 = ,∠A=∠D,则△ABC∽△DEF.
1. 如图,四边形ABCD的对角线AC、BD相交于点O,且将这个四边形分成①②③④四个三角形.若 OA∶OC=OB∶OD,则下列结论正确的是 ( )
A. ①和②相似 B. ①和③相似 C. ①和④相似 D. ②和④相似
2. 如图,AD=3,AB=5,AC=6,要使△ADE与△ABC相似,AE的长应为 ( )
A. B. C. D. 或
3. 如图,AD·AB=AE·AC.若∠A=60°,∠B=50°,则∠ADE= .
4. 如图,AB⊥CB于点B,AC⊥CD于点C,AB=6,AC=10,则当CD的值为 时,△ABC∽△ACD.
5. (2024·广州)如图,点E、F分别在正方形ABCD的边BC、CD上,BE=3,EC=6,CF=2.求证:△ABE∽△ECF.
第5题
第4课时 用三边的关系判定三角形相似
1. 三角形相似的判定定理:三边 的两个三角形相似.
2. 在△ABC和△DEF中,若 = = ,则△ABC∽△DEF.
1. 有甲、乙两个三角形木框,甲的三边长分别为1、、,乙的三边长分别为5、、,则甲、乙两个三角形木框 ( )
A. 全等 B. 相似 C. 不相似 D. 周长相等
2. △ABC的三边长分别为7、6、2,△A1B1C1的两边长分别为1、3,要使△ABC∽△A1B1C1,则△A1B1C1的第三边的长应为 ( )
A. B. 2 C. D.
3. 如图,在由边长为1的小正方形组成的网格中有6个斜三角形:① △ABC;② △BCD;③ △BDE;④ △BFG;⑤ △FGH;⑥ △EFK.在②~⑥中,与①相似的是 (填序号).
4. 已知△ABC的三边长分别为6、、9,△MNP的一边长为4,则当△MNP其余两边的长分别为 时,这两个三角形相似.
5. 如图,在△ABC和△AED中,AB=25,BC=40,AC=20,AE=12,AD=15,DE=24.
(1) 求证:△ABC∽△ADE;
(2) 若∠BAC=125°,∠EAC=70°,求∠CAD的度数.
第5题
第5课时 与判定三角形相似有关的应用及三角形的重心
1. 判定两个三角形相似的基本思路:
(1) 若已知一对等角,则可找另一对 角,或找夹已知等角的两边 ;
(2) 若已知两边成比例,则可找其 相等,或找 也成比例.
2. 三角形的三条 相交于一点,这个点叫做三角形的重心.三角形的重心到三角形一个顶点的距离是它到这个顶点对边中点的距离的 .
1. 如图,AB=2AD,AC=2AE,要使△ABC∽△ADE,下列添加的条件错误的是 ( )
A. ∠DAC=∠CAE B. ∠BAD=∠CAE
C. ∠BAC=∠DAE D. BC∶DE=2∶1
2. 如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E.如果CB=8,那么GE的长为 .
3. (2024·南充)如图,直线y=kx+b经过A(0,-2)、B(-1,0)两点,与双曲线y=在第二象限内的一支交于点C(a,2),过点C作CD⊥x轴于点D.若点P在x轴上,以O、A、P为顶点的三角形与△BCD相似,则点P的坐标为 .
4. 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于点G.求证:==.
第4题
6.4 探索三角形相似的条件
第1课时 平行线分线段成比例
及平行线截三角形相似
1. 成比例 2. 相似
1. A 2. B 3. 1 4. 1
5. ∵ EC∥AB,即ED∥AB,∴ △FAB∽△FEC,△OAB∽△OED,∠C=∠ABF.∵ ∠EDA=∠ABF,∴ ∠C=∠EDA.∴ AD∥CF,即AD∥BF.∴ △AED∽△FEC,△OFB∽△OAD.∴ △FAB∽△AED
第2课时 用两角的关系判定三角形相似
1. 分别相等 2. 两 ACD CBD
1. C 2. C 3. 答案不唯一,如∠A=∠C 4.
5. (1) ∵ AD是斜边BC上的高,∴ ∠BDA=90°.∵ ∠BAC=90°,∴ ∠BDA=∠BAC.又∵ ∠B=∠B,∴ △ABD∽△CBA (2) 由(1),知△ABD∽△CBA,∴ =.∵ AB=6,BC=10,∴ =.∴ BD=3.6
第3课时 用两边及夹角的关系判定三角形相似
1. 成比例 夹角相等 2.
1. B 2. D 3. 70° 4.
5. ∵ BE=3,EC=6,∴ BC=3+6=9.∵ 四边形ABCD是正方形,∴ AB=BC=9,∠B=∠C=90°.∵ ==,=,∴ =.∴ △ABE∽△ECF
第4课时 用三边的关系判定三角形相似
1. 成比例 2.
1. B 2. C 3. ③④⑤ 4. 5、6或、或、
5. (1) ∵ BC∶DE=40∶24=5∶3,AB∶AD=25∶15=5∶3,AC∶AE=20∶12=5∶3,∴ BC∶DE=AB∶AD=AC∶AE.∴ △ABC∽△ADE (2) ∵ △ABC∽△ADE,∴ ∠BAC=∠DAE=125°.又∵ ∠EAC=70°,∴ ∠CAD=∠DAE-∠EAC=55°
第5课时 与判定三角形相似
有关的应用及三角形的重心
1. (1) 等 成比例 (2) 夹角 第三边 2. 中线 2倍
1. A 2. 3. (-4,0)或(-1,0)或(1,0)或(4,0)
4. 连接ED.∵ D、E分别是边BC、AB的中点,∴ DE∥AC,=.∴ 易得△DEG∽△ACG.∴ ===.∴ 易得==
第1课时 平行线分线段成比例及平行线截三角形相似
1. 两条直线被一组平行线所截,所得的对应线段 .
2. 平行于三角形一边的直线与其他两边相交,所截得的三角形与原三角形 .
1. (2023·吉林)如图,在△ABC中,点D在边AB上,过点D作DE∥BC,交AC于点E.若AD=2,BD=3,则的值是 ( )
A. B. C. D.
2. (2024·湖南改编)如图,在△ABC中,D、E分别为边AB、AC的中点.下列结论错误的是 ( )
A. △ADE∽△ABC B. △ADE与△ABC的相似比是2
C. DE∶BC=1∶2 D. ∠AED=∠C
3. 如图,直线l1∥l2∥l3,另有两条直线分别交l1、l2、l3于点A、B、C及点D、E、F,且AB=3,DE=6,EF=2,则BC的长为 .
4. (2024·河南)如图,在 ABCD中,对角线AC、BD相交于点O,E为OC的中点,EF∥AB,交BC于点F.若AB=4,则EF的长为 .
5. 如图,EC∥AB,∠EDA=∠ABF.指出图中所有的相似三角形(不含相似比为1的相似三角形).
第5题
第2课时 用两角的关系判定三角形相似
1. 三角形相似的判定定理:两角 的两个三角形相似.
2. 如图,根据三角形相似的判定定理,可以知道直角三角形被斜边上的高分成的 个小直角三角形与原直角三角形相似,即△ ∽△ ∽△ABC.
1.
下列各对三角形中,不一定相似的是 ( )
2. (2023·东营)如图,△ABC为等边三角形,点D、E分别在边BC、AB上,∠ADE=60°.若BD=4DC,DE=2.4,则AD的长为 ( )
A. 1.8 B. 2.4 C. 3 D. 3.2
3. (2024·青海)如图,AC和BD相交于点O,请你添加一个条件: ,使得△AOB∽△COD(写出一个即可).
4. 如图,∠ABC=∠ACD.若AD=3cm,AB=7cm,则AC= cm.
5. (2024·济南改编)如图,在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1) 求证:△ABD∽△CBA;
(2) 若AB=6,BC=10,求BD的长.
第5题
第3课时 用两边及夹角的关系判定三角形相似
1. 三角形相似的判定定理:两边 且 的两个三角形相似.
2. 在△ABC和△DEF中,若 = ,∠A=∠D,则△ABC∽△DEF.
1. 如图,四边形ABCD的对角线AC、BD相交于点O,且将这个四边形分成①②③④四个三角形.若 OA∶OC=OB∶OD,则下列结论正确的是 ( )
A. ①和②相似 B. ①和③相似 C. ①和④相似 D. ②和④相似
2. 如图,AD=3,AB=5,AC=6,要使△ADE与△ABC相似,AE的长应为 ( )
A. B. C. D. 或
3. 如图,AD·AB=AE·AC.若∠A=60°,∠B=50°,则∠ADE= .
4. 如图,AB⊥CB于点B,AC⊥CD于点C,AB=6,AC=10,则当CD的值为 时,△ABC∽△ACD.
5. (2024·广州)如图,点E、F分别在正方形ABCD的边BC、CD上,BE=3,EC=6,CF=2.求证:△ABE∽△ECF.
第5题
第4课时 用三边的关系判定三角形相似
1. 三角形相似的判定定理:三边 的两个三角形相似.
2. 在△ABC和△DEF中,若 = = ,则△ABC∽△DEF.
1. 有甲、乙两个三角形木框,甲的三边长分别为1、、,乙的三边长分别为5、、,则甲、乙两个三角形木框 ( )
A. 全等 B. 相似 C. 不相似 D. 周长相等
2. △ABC的三边长分别为7、6、2,△A1B1C1的两边长分别为1、3,要使△ABC∽△A1B1C1,则△A1B1C1的第三边的长应为 ( )
A. B. 2 C. D.
3. 如图,在由边长为1的小正方形组成的网格中有6个斜三角形:① △ABC;② △BCD;③ △BDE;④ △BFG;⑤ △FGH;⑥ △EFK.在②~⑥中,与①相似的是 (填序号).
4. 已知△ABC的三边长分别为6、、9,△MNP的一边长为4,则当△MNP其余两边的长分别为 时,这两个三角形相似.
5. 如图,在△ABC和△AED中,AB=25,BC=40,AC=20,AE=12,AD=15,DE=24.
(1) 求证:△ABC∽△ADE;
(2) 若∠BAC=125°,∠EAC=70°,求∠CAD的度数.
第5题
第5课时 与判定三角形相似有关的应用及三角形的重心
1. 判定两个三角形相似的基本思路:
(1) 若已知一对等角,则可找另一对 角,或找夹已知等角的两边 ;
(2) 若已知两边成比例,则可找其 相等,或找 也成比例.
2. 三角形的三条 相交于一点,这个点叫做三角形的重心.三角形的重心到三角形一个顶点的距离是它到这个顶点对边中点的距离的 .
1. 如图,AB=2AD,AC=2AE,要使△ABC∽△ADE,下列添加的条件错误的是 ( )
A. ∠DAC=∠CAE B. ∠BAD=∠CAE
C. ∠BAC=∠DAE D. BC∶DE=2∶1
2. 如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E.如果CB=8,那么GE的长为 .
3. (2024·南充)如图,直线y=kx+b经过A(0,-2)、B(-1,0)两点,与双曲线y=在第二象限内的一支交于点C(a,2),过点C作CD⊥x轴于点D.若点P在x轴上,以O、A、P为顶点的三角形与△BCD相似,则点P的坐标为 .
4. 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于点G.求证:==.
第4题
6.4 探索三角形相似的条件
第1课时 平行线分线段成比例
及平行线截三角形相似
1. 成比例 2. 相似
1. A 2. B 3. 1 4. 1
5. ∵ EC∥AB,即ED∥AB,∴ △FAB∽△FEC,△OAB∽△OED,∠C=∠ABF.∵ ∠EDA=∠ABF,∴ ∠C=∠EDA.∴ AD∥CF,即AD∥BF.∴ △AED∽△FEC,△OFB∽△OAD.∴ △FAB∽△AED
第2课时 用两角的关系判定三角形相似
1. 分别相等 2. 两 ACD CBD
1. C 2. C 3. 答案不唯一,如∠A=∠C 4.
5. (1) ∵ AD是斜边BC上的高,∴ ∠BDA=90°.∵ ∠BAC=90°,∴ ∠BDA=∠BAC.又∵ ∠B=∠B,∴ △ABD∽△CBA (2) 由(1),知△ABD∽△CBA,∴ =.∵ AB=6,BC=10,∴ =.∴ BD=3.6
第3课时 用两边及夹角的关系判定三角形相似
1. 成比例 夹角相等 2.
1. B 2. D 3. 70° 4.
5. ∵ BE=3,EC=6,∴ BC=3+6=9.∵ 四边形ABCD是正方形,∴ AB=BC=9,∠B=∠C=90°.∵ ==,=,∴ =.∴ △ABE∽△ECF
第4课时 用三边的关系判定三角形相似
1. 成比例 2.
1. B 2. C 3. ③④⑤ 4. 5、6或、或、
5. (1) ∵ BC∶DE=40∶24=5∶3,AB∶AD=25∶15=5∶3,AC∶AE=20∶12=5∶3,∴ BC∶DE=AB∶AD=AC∶AE.∴ △ABC∽△ADE (2) ∵ △ABC∽△ADE,∴ ∠BAC=∠DAE=125°.又∵ ∠EAC=70°,∴ ∠CAD=∠DAE-∠EAC=55°
第5课时 与判定三角形相似
有关的应用及三角形的重心
1. (1) 等 成比例 (2) 夹角 第三边 2. 中线 2倍
1. A 2. 3. (-4,0)或(-1,0)或(1,0)或(4,0)
4. 连接ED.∵ D、E分别是边BC、AB的中点,∴ DE∥AC,=.∴ 易得△DEG∽△ACG.∴ ===.∴ 易得==
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
