7.1 正切 同步练习(2课时,含答案)2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 7.1 正切 同步练习(2课时,含答案)2024-2025学年数学苏科版九年级下册 | 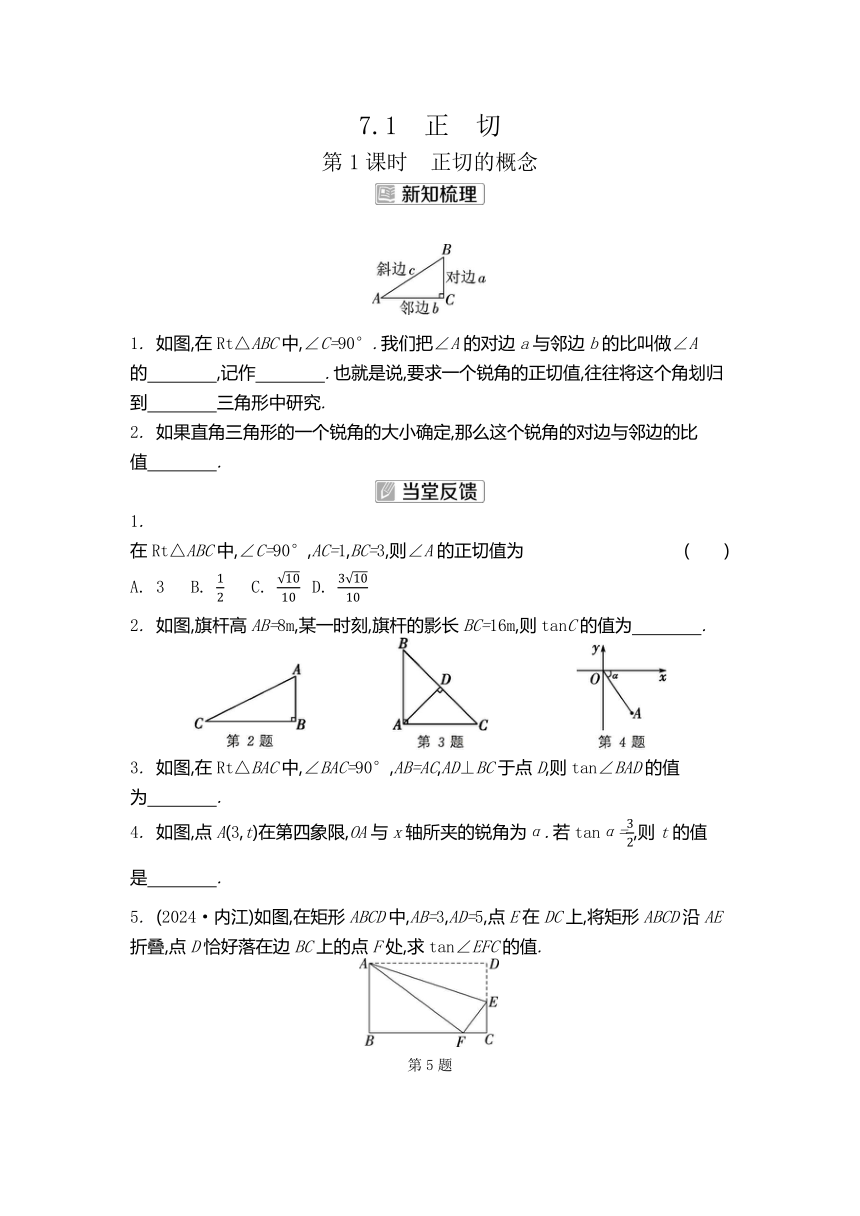 | |
| 格式 | docx | ||
| 文件大小 | 90.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 14:39:51 | ||
图片预览

文档简介
7.1 正 切
第1课时 正切的概念
1. 如图,在Rt△ABC中,∠C=90°.我们把∠A的对边a与邻边b的比叫做∠A的 ,记作 .也就是说,要求一个锐角的正切值,往往将这个角划归到 三角形中研究.
2. 如果直角三角形的一个锐角的大小确定,那么这个锐角的对边与邻边的比值 .
1.
在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为 ( )
A. 3 B. C. D.
2. 如图,旗杆高AB=8m,某一时刻,旗杆的影长BC=16m,则tanC的值为 .
3. 如图,在Rt△BAC中,∠BAC=90°,AB=AC,AD⊥BC于点D,则tan∠BAD的值为 .
4. 如图,点A(3,t)在第四象限,OA与x轴所夹的锐角为α.若tanα=,则t的值是 .
5. (2024·内江)如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在边BC上的点F处,求tan∠EFC的值.
第5题
第2课时 正切的增减性及计算
1. 当锐角α越来越大时,α的正切值越来 .
2. 直角三角形中锐角的正切值,揭示了直角三角形的两直角边之间的数量关系,因此,知道直角三角形的一个锐角大小和一条直角边长,可以求得 .
1.
如图,在Rt△ABC中,∠C=90°,∠A=α,下列说法正确的是 ( )
A. α越大,BC的长不变 B. α越大,BC的长越小
C. α越大,BC与AC的比值越大 D. α越大,AC与BC的比值越大
2. 用计算器计算:tan80°≈ ,tan44°≈ (精确到0.01).
3. 比较tan46°、tan35°与tan79°的大小: (用“<”连接).
4. 如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,将△ABC绕点A按逆时针方向旋转得到△ADE,使得点D落在边AC上,则tan∠ECD的值为 .
5. 如图,在平面直角坐标系中,O为坐标原点,点E的坐标为(0,4),点C在☉A上,BE是☉A的一条弦.若tan∠OBE=,则☉A的直径为 .
6. (2023·巴中)如图,在正方形ABCD和正方形BEFG中,点G在AD上,GF与CD交于点H,连接BH,tan∠ABG=,正方形ABCD的边长为8,求BH的长.
第6题
7.1 正 切
第1课时 正切的概念
1. 正切 tanA 直角 2. 也确定
1. A 2. 3. 1 4. -
5. ∵ 四边形ABCD为矩形,∴ ∠B=∠D=90°.∴ 在Rt△ABF中,∠BAF+∠AFB=90°.由折叠的性质,得AF=AD=5,∠AFE=∠D=90°,∴ ∠EFC+∠AFB=90°.∴ ∠EFC=∠BAF.∵ AB=3,∴ 在Rt△ABF中,由勾股定理,得BF===4.∴ tan∠BAF==.∴ tan∠EFC=tan∠BAF=
第2课时 正切的增减性及计算
1. 越大 2. 另一条直角边长
1. C 2. 5.67 0.97 3. tan35°6. ∵ 四边形ABCD、BEFG均为正方形,∴ ∠A=∠BGF=∠D=90°.∴ ∠AGB+∠DGH=90°,∠AGB+∠ABG=90°.∴ ∠ABG=∠DGH.∴ △BAG∽△GDH.∴ =.∵ 正方形ABCD的边长为8,∴ AB=AD=8.∴ 在Rt△ABG中,AG=AB·tan∠ABG=4.∴ BG==4,DG=AD-AG=4.∴ =,解得GH=2.∴ 在Rt△BGH中,BH==10
第1课时 正切的概念
1. 如图,在Rt△ABC中,∠C=90°.我们把∠A的对边a与邻边b的比叫做∠A的 ,记作 .也就是说,要求一个锐角的正切值,往往将这个角划归到 三角形中研究.
2. 如果直角三角形的一个锐角的大小确定,那么这个锐角的对边与邻边的比值 .
1.
在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为 ( )
A. 3 B. C. D.
2. 如图,旗杆高AB=8m,某一时刻,旗杆的影长BC=16m,则tanC的值为 .
3. 如图,在Rt△BAC中,∠BAC=90°,AB=AC,AD⊥BC于点D,则tan∠BAD的值为 .
4. 如图,点A(3,t)在第四象限,OA与x轴所夹的锐角为α.若tanα=,则t的值是 .
5. (2024·内江)如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在边BC上的点F处,求tan∠EFC的值.
第5题
第2课时 正切的增减性及计算
1. 当锐角α越来越大时,α的正切值越来 .
2. 直角三角形中锐角的正切值,揭示了直角三角形的两直角边之间的数量关系,因此,知道直角三角形的一个锐角大小和一条直角边长,可以求得 .
1.
如图,在Rt△ABC中,∠C=90°,∠A=α,下列说法正确的是 ( )
A. α越大,BC的长不变 B. α越大,BC的长越小
C. α越大,BC与AC的比值越大 D. α越大,AC与BC的比值越大
2. 用计算器计算:tan80°≈ ,tan44°≈ (精确到0.01).
3. 比较tan46°、tan35°与tan79°的大小: (用“<”连接).
4. 如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,将△ABC绕点A按逆时针方向旋转得到△ADE,使得点D落在边AC上,则tan∠ECD的值为 .
5. 如图,在平面直角坐标系中,O为坐标原点,点E的坐标为(0,4),点C在☉A上,BE是☉A的一条弦.若tan∠OBE=,则☉A的直径为 .
6. (2023·巴中)如图,在正方形ABCD和正方形BEFG中,点G在AD上,GF与CD交于点H,连接BH,tan∠ABG=,正方形ABCD的边长为8,求BH的长.
第6题
7.1 正 切
第1课时 正切的概念
1. 正切 tanA 直角 2. 也确定
1. A 2. 3. 1 4. -
5. ∵ 四边形ABCD为矩形,∴ ∠B=∠D=90°.∴ 在Rt△ABF中,∠BAF+∠AFB=90°.由折叠的性质,得AF=AD=5,∠AFE=∠D=90°,∴ ∠EFC+∠AFB=90°.∴ ∠EFC=∠BAF.∵ AB=3,∴ 在Rt△ABF中,由勾股定理,得BF===4.∴ tan∠BAF==.∴ tan∠EFC=tan∠BAF=
第2课时 正切的增减性及计算
1. 越大 2. 另一条直角边长
1. C 2. 5.67 0.97 3. tan35°
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
