7.6 用锐角三角函数解决问题 同步练习(3课时,含答案)2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 7.6 用锐角三角函数解决问题 同步练习(3课时,含答案)2024-2025学年数学苏科版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 155.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览


文档简介
7.6 用锐角三角函数解决问题
第1课时 与坡度和坡角有关的问题
1. 坡面与 的夹角叫做坡角.坡面的铅垂 与水平 的比叫做坡度(或坡比),记作i,即i= (坡角用α表示),坡度通常用1∶m的形式表示.
2. 在水利工程实际问题中,实际上就是将水坝的横截面看成一个梯形,分别过梯形上底的两个顶点作出下底的高,将梯形分成两个 三角形和一个 ,从而将问题转化为直角三角形问题进行解答.
1. (2023·深圳)如图,坡面与水平面的夹角为α,则爬坡时每爬1m耗能(1.025-cosα)J.若某人爬了1000m,该坡角为30°,则他大约耗能(参考数据:≈1.732,≈1.414) ( )
A. 58J B. 159J C. 1025J D. 1732J
2. (2024·济南改编)如图,某地修建的一座建筑物的截面图的高BC=5m,坡面AB的坡度为1∶,则AB的长为 ( )
A. 10m B. 10m C. 5m D. 5m
3. 若斜坡的坡度i=1∶,则坡角为 (精确到0.1°).
4. 如图,某山坡的坡面AB=200m,坡角∠BAC=45°,则该山坡的高BC为 m.
5. 如图,信号塔PQ坐落在坡度i=1∶2的斜坡上,其正前方直立着一块警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN的长为2m,落在警示牌上的影子MN的长为3m.求信号塔PQ的高.
第5题
第2课时 与旋转等有关的问题
1. 对于生活中的实际问题,我们要能够将实际问题抽象成几何问题,画出几何图形,通过图形反映问题中的已知与 及已知量与 之间的关系.
2. 如图,OB、OC分别为☉O的半径,且半径为r,CD⊥OA,垂足为D,∠AOC=α,点O到直线l的距离OA为m,则点C到直线l的距离为 .
1. (2024·包头改编)如图,某旗杆AB的高为10m,拉线AC的长与旗杆AB的高相等,现将拉线末端向外拉30°,此时拉线末端C与地面的距离是 ( )
A. 5m B. 5m C. (10-5)m D. (10-)m
2. (2023·枣庄)如图,桔槔是一种原始的汲水工具,它是在一根竖立的架子上加上一根细长的杠杆,末端悬挂一重物,前端悬挂水桶.当人把水桶放入水中打满水以后,由于杠杆末端的重力作用,便能轻易把水提升至所需处.已知杠杆AB=6m,AO∶OB=2∶1,支架OM⊥EF,OM=3m,AB可以绕着点O自由旋转.当点A旋转到如图所示的位置时,∠AOM=45°,此时点B到水平地面EF的距离为 m(结果保留根号).
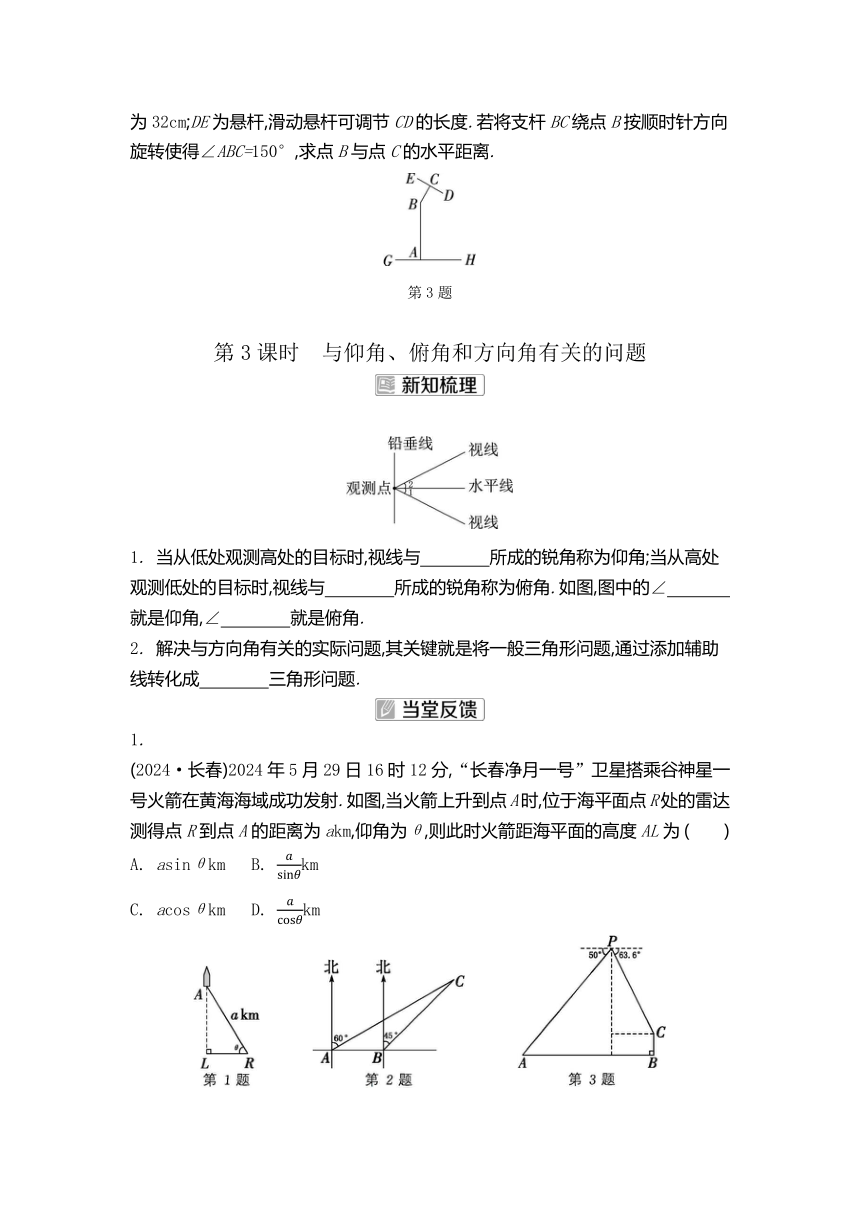
3. 如图所示为某种落地灯的侧面示意图,GH为落地灯底座,其高度忽略不计,点D为灯罩和灯泡,AB为立杆,其高为95cm;BC为支杆,它可以绕点B旋转,其中BC的长为32cm;DE为悬杆,滑动悬杆可调节CD的长度.若将支杆BC绕点B按顺时针方向旋转使得∠ABC=150°,求点B与点C的水平距离.
第3题
第3课时 与仰角、俯角和方向角有关的问题
1. 当从低处观测高处的目标时,视线与 所成的锐角称为仰角;当从高处观测低处的目标时,视线与 所成的锐角称为俯角.如图,图中的∠ 就是仰角,∠ 就是俯角.
2. 解决与方向角有关的实际问题,其关键就是将一般三角形问题,通过添加辅助线转化成 三角形问题.
1.
(2024·长春)2024年5月29日16时12分,“长春净月一号”卫星搭乘谷神星一号火箭在黄海海域成功发射.如图,当火箭上升到点A时,位于海平面点R处的雷达测得点R到点A的距离为akm,仰角为θ,则此时火箭距海平面的高度AL为 ( )
A. asinθkm B. km
C. acosθkm D. km
2. (2023·眉山)如图,一渔船在海上点A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向.若渔船继续向正东方向航行,则渔船与灯塔C之间的最短距离是 海里.
3. (2024·泰安)在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一架无人机.如图,无人机在河上方距水面高60m的点P处测得瞭望台正对岸点A处的俯角为50°,测得瞭望台顶端C处的俯角为63.6°,已知瞭望台BC高12m(图中点A、B、C、P在同一平面内),那么大汶河此河段的宽AB约为 m.
4. (2024·吉林改编)如图,O、R是同一水平线上的两点,无人机从点O竖直上升到点A时,测得点A到点R的距离为40m,点R的俯角为24.2°,无人机继续竖直上升到点B,测得点R的俯角为36.9°.求无人机从点A到点B的上升高度AB(精确到0.1m,参考数据:sin24.2°≈0.41,cos24.2°≈0.91,tan24.2°≈0.45,sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75).
第4题
5. (2024·天津)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔AB的高度(如图①).某学习小组设计了一个方案:如图②,点C、D、E依次在同一条水平直线上,DE=36m,EC⊥AB,垂足为C.在点D处测得桥塔顶部B的仰角(∠CDB)为45°,测得桥塔底部A的俯角(∠CDA)为6°,又在点E处测得桥塔顶部B的仰角(∠CEB)为31°(结果保留整数,参考数据:tan31°≈0.6,tan6°≈0.1).求:
(1) 线段CD的长;
(2) 桥塔AB的高度.
7.6 用锐角三角函数解决问题
第1课时 与坡度和坡角有关的问题
1. 水平面 高度 宽度 tanα 2. 直角 矩形
1. B 2. A 3. 24.1° 4. 100
5. 过点M作MF⊥PQ于点F,过点Q作QE⊥MN于点E.∴ 易得MN∥PQ,四边形QEMF是矩形.∴ FQ=EM,EQ=MF.在Rt△QEN中,设EN=xm(x>0).由题意,易得斜坡QN的坡度i=tan∠EQN=1∶2,∴ EQ=2EN=2xm.在Rt△QEN中,由勾股定理,得EN2+EQ2=QN2,即x2+(2x)2=(2)2,解得x=2(负值舍去).∴ EN=2m,EQ=MF=4m.∵ MN=3m,∴ FQ=EM=1m.根据题意,得∠PMF=60°.∵ 在Rt△PFM中,tan∠PMF=,∴ PF=MF·tan60°=4m.∴ PQ=PF+FQ=(4+1)m.∴ 信号塔PQ的高为(4+1)m
第2课时 与旋转等有关的问题
1. 未知 未知量 2. m-r·cosα
1. C 2. (3+)
3. 过点B作BF∥GH,过点C作CQ⊥BF于点Q.由题意,得∠HAB=90°,∴ ∠ABF=90°.∵ ∠ABC=150°,∴ ∠CBF=∠ABC-∠ABF=60°.∵ BC=32cm,∴ BQ=BC·cos∠CBF=16cm.∴ 点B与点C的水平距离为16cm
第3课时 与仰角、俯角和方向角有关的问题
1. 水平线 水平线 2 1 2. 直角
1. A 2. (6+6) 3. 74
4. 由题意,得∠ORB=36.9°,∠ORA=24.2°,∠BOR=90°.∵ 在Rt△AOR中,AR=40m,∠ORA=24.2°,∴ OA=AR·sin∠ORA≈16.4m,OR=AR·cos∠ORA≈36.4m.∴ 在Rt△BOR中,OB=OR·tan∠ORB≈27.3m.∴ AB=OB-OA=10.9m.∴ 无人机从点A到点B的上升高度AB约为10.9m
5. (1) 设CD=xm.∵ DE=36m,∴ CE=CD+DE=(x+36)m.∵ EC⊥AB,∴ ∠BCE=∠ACD=90°.∵ 在Rt△BCD中,tan∠CDB=,∠CDB=45°,∴ BC=CD·tan∠CDB=x·tan45°=x(m).∵ 在Rt△BCE中,tan∠CEB=,∠CEB=31°,∴ BC=CE·tan∠CEB≈(0.6x+21.6)m.∴ x=0.6x+21.6,解得x=54.∴ 线段CD的长约为54m (2) ∵ 在Rt△ACD中,tan∠CDA=,∠CDA=6°,∴ AC=CD·tan∠CDA≈54×0.1=5.4(m).∴ AB=AC+BC=5.4+54≈59(m).∴ 桥塔AB的高度约为59m
第1课时 与坡度和坡角有关的问题
1. 坡面与 的夹角叫做坡角.坡面的铅垂 与水平 的比叫做坡度(或坡比),记作i,即i= (坡角用α表示),坡度通常用1∶m的形式表示.
2. 在水利工程实际问题中,实际上就是将水坝的横截面看成一个梯形,分别过梯形上底的两个顶点作出下底的高,将梯形分成两个 三角形和一个 ,从而将问题转化为直角三角形问题进行解答.
1. (2023·深圳)如图,坡面与水平面的夹角为α,则爬坡时每爬1m耗能(1.025-cosα)J.若某人爬了1000m,该坡角为30°,则他大约耗能(参考数据:≈1.732,≈1.414) ( )
A. 58J B. 159J C. 1025J D. 1732J
2. (2024·济南改编)如图,某地修建的一座建筑物的截面图的高BC=5m,坡面AB的坡度为1∶,则AB的长为 ( )
A. 10m B. 10m C. 5m D. 5m
3. 若斜坡的坡度i=1∶,则坡角为 (精确到0.1°).
4. 如图,某山坡的坡面AB=200m,坡角∠BAC=45°,则该山坡的高BC为 m.
5. 如图,信号塔PQ坐落在坡度i=1∶2的斜坡上,其正前方直立着一块警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN的长为2m,落在警示牌上的影子MN的长为3m.求信号塔PQ的高.
第5题
第2课时 与旋转等有关的问题
1. 对于生活中的实际问题,我们要能够将实际问题抽象成几何问题,画出几何图形,通过图形反映问题中的已知与 及已知量与 之间的关系.
2. 如图,OB、OC分别为☉O的半径,且半径为r,CD⊥OA,垂足为D,∠AOC=α,点O到直线l的距离OA为m,则点C到直线l的距离为 .
1. (2024·包头改编)如图,某旗杆AB的高为10m,拉线AC的长与旗杆AB的高相等,现将拉线末端向外拉30°,此时拉线末端C与地面的距离是 ( )
A. 5m B. 5m C. (10-5)m D. (10-)m
2. (2023·枣庄)如图,桔槔是一种原始的汲水工具,它是在一根竖立的架子上加上一根细长的杠杆,末端悬挂一重物,前端悬挂水桶.当人把水桶放入水中打满水以后,由于杠杆末端的重力作用,便能轻易把水提升至所需处.已知杠杆AB=6m,AO∶OB=2∶1,支架OM⊥EF,OM=3m,AB可以绕着点O自由旋转.当点A旋转到如图所示的位置时,∠AOM=45°,此时点B到水平地面EF的距离为 m(结果保留根号).
3. 如图所示为某种落地灯的侧面示意图,GH为落地灯底座,其高度忽略不计,点D为灯罩和灯泡,AB为立杆,其高为95cm;BC为支杆,它可以绕点B旋转,其中BC的长为32cm;DE为悬杆,滑动悬杆可调节CD的长度.若将支杆BC绕点B按顺时针方向旋转使得∠ABC=150°,求点B与点C的水平距离.
第3题
第3课时 与仰角、俯角和方向角有关的问题
1. 当从低处观测高处的目标时,视线与 所成的锐角称为仰角;当从高处观测低处的目标时,视线与 所成的锐角称为俯角.如图,图中的∠ 就是仰角,∠ 就是俯角.
2. 解决与方向角有关的实际问题,其关键就是将一般三角形问题,通过添加辅助线转化成 三角形问题.
1.
(2024·长春)2024年5月29日16时12分,“长春净月一号”卫星搭乘谷神星一号火箭在黄海海域成功发射.如图,当火箭上升到点A时,位于海平面点R处的雷达测得点R到点A的距离为akm,仰角为θ,则此时火箭距海平面的高度AL为 ( )
A. asinθkm B. km
C. acosθkm D. km
2. (2023·眉山)如图,一渔船在海上点A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向.若渔船继续向正东方向航行,则渔船与灯塔C之间的最短距离是 海里.
3. (2024·泰安)在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一架无人机.如图,无人机在河上方距水面高60m的点P处测得瞭望台正对岸点A处的俯角为50°,测得瞭望台顶端C处的俯角为63.6°,已知瞭望台BC高12m(图中点A、B、C、P在同一平面内),那么大汶河此河段的宽AB约为 m.
4. (2024·吉林改编)如图,O、R是同一水平线上的两点,无人机从点O竖直上升到点A时,测得点A到点R的距离为40m,点R的俯角为24.2°,无人机继续竖直上升到点B,测得点R的俯角为36.9°.求无人机从点A到点B的上升高度AB(精确到0.1m,参考数据:sin24.2°≈0.41,cos24.2°≈0.91,tan24.2°≈0.45,sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75).
第4题
5. (2024·天津)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔AB的高度(如图①).某学习小组设计了一个方案:如图②,点C、D、E依次在同一条水平直线上,DE=36m,EC⊥AB,垂足为C.在点D处测得桥塔顶部B的仰角(∠CDB)为45°,测得桥塔底部A的俯角(∠CDA)为6°,又在点E处测得桥塔顶部B的仰角(∠CEB)为31°(结果保留整数,参考数据:tan31°≈0.6,tan6°≈0.1).求:
(1) 线段CD的长;
(2) 桥塔AB的高度.
7.6 用锐角三角函数解决问题
第1课时 与坡度和坡角有关的问题
1. 水平面 高度 宽度 tanα 2. 直角 矩形
1. B 2. A 3. 24.1° 4. 100
5. 过点M作MF⊥PQ于点F,过点Q作QE⊥MN于点E.∴ 易得MN∥PQ,四边形QEMF是矩形.∴ FQ=EM,EQ=MF.在Rt△QEN中,设EN=xm(x>0).由题意,易得斜坡QN的坡度i=tan∠EQN=1∶2,∴ EQ=2EN=2xm.在Rt△QEN中,由勾股定理,得EN2+EQ2=QN2,即x2+(2x)2=(2)2,解得x=2(负值舍去).∴ EN=2m,EQ=MF=4m.∵ MN=3m,∴ FQ=EM=1m.根据题意,得∠PMF=60°.∵ 在Rt△PFM中,tan∠PMF=,∴ PF=MF·tan60°=4m.∴ PQ=PF+FQ=(4+1)m.∴ 信号塔PQ的高为(4+1)m
第2课时 与旋转等有关的问题
1. 未知 未知量 2. m-r·cosα
1. C 2. (3+)
3. 过点B作BF∥GH,过点C作CQ⊥BF于点Q.由题意,得∠HAB=90°,∴ ∠ABF=90°.∵ ∠ABC=150°,∴ ∠CBF=∠ABC-∠ABF=60°.∵ BC=32cm,∴ BQ=BC·cos∠CBF=16cm.∴ 点B与点C的水平距离为16cm
第3课时 与仰角、俯角和方向角有关的问题
1. 水平线 水平线 2 1 2. 直角
1. A 2. (6+6) 3. 74
4. 由题意,得∠ORB=36.9°,∠ORA=24.2°,∠BOR=90°.∵ 在Rt△AOR中,AR=40m,∠ORA=24.2°,∴ OA=AR·sin∠ORA≈16.4m,OR=AR·cos∠ORA≈36.4m.∴ 在Rt△BOR中,OB=OR·tan∠ORB≈27.3m.∴ AB=OB-OA=10.9m.∴ 无人机从点A到点B的上升高度AB约为10.9m
5. (1) 设CD=xm.∵ DE=36m,∴ CE=CD+DE=(x+36)m.∵ EC⊥AB,∴ ∠BCE=∠ACD=90°.∵ 在Rt△BCD中,tan∠CDB=,∠CDB=45°,∴ BC=CD·tan∠CDB=x·tan45°=x(m).∵ 在Rt△BCE中,tan∠CEB=,∠CEB=31°,∴ BC=CE·tan∠CEB≈(0.6x+21.6)m.∴ x=0.6x+21.6,解得x=54.∴ 线段CD的长约为54m (2) ∵ 在Rt△ACD中,tan∠CDA=,∠CDA=6°,∴ AC=CD·tan∠CDA≈54×0.1=5.4(m).∴ AB=AC+BC=5.4+54≈59(m).∴ 桥塔AB的高度约为59m
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
