8.1 中学生的视力情况调查 练习(2课时、含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 8.1 中学生的视力情况调查 练习(2课时、含答案) 2024-2025学年数学苏科版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 208.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览

文档简介
8.1 中学生的视力情况调查
第1课时 简单随机抽样
1. 抽样调查是从总体中抽取样本进行调查,根据样本来估计 的一种调查方式.为了获得较为准确的调查结果,抽样时要注意样本的 性和广泛性.
2. 一般地,从个体总数为N的总体中抽取容量为n的样本(n1.
(2024·赤峰改编)下列调查中,适宜采用抽样调查的是 ( )
A. 调查某班学生的身高情况
B. 调查亚运会100m游泳决赛运动员的身体状况
C. 调查某品牌新能源汽车的最大续航里程
D. 检测“神舟十六号”飞船的零部件
2. 想要调查某大型企业员工对企业的满意度,有下列选取的调查对象:① 企业的男员工;② 企业年满40岁的员工;③ 借助企业人员名册,随机抽取四分之一的员工;④ 企业新进员工.其中,具有代表性的是 (填序号).
第3题
3. 某校拟开设四门校本课程供学生选择:A.文学鉴赏;B. 趣味数学;C. 川行历史;D. 航模科技.为了解该校八年级1000名学生对四门校本课程的选择意向,张老师做了以下工作:① 抽取40名学生作为调查对象;② 整理数据并绘制统计图;③ 收集40名学生对四门课程的选择意向的相关数据;④ 结合统计图分析数据并得出结论.
(1) 请对张老师的工作步骤正确排序: (填序号).
(2) 以上步骤中,抽取40名学生最合适的方式为 ( )
A. 随机抽取八年级(3)班的40名学生 B. 随机抽取八年级40名男生
C. 随机抽取八年级40名女生 D. 随机抽取八年级40名学生
(3) 如图所示为张老师绘制的40名学生所选课程类型的条形统计图.假设全年级每名学生都做出了选择,且只选择了一门课程.若学校规定每个班级不超过40人,请你根据上述信息,估计该校八年级至少应该开设 个趣味数学班.
4. (2024·通辽)为迎接2024年5月26日的科尔沁马拉松赛事,某中学九年级提前开展了一次“马拉松”历史知识测试.九年级600名学生全部参加本次测试,调查研究小组随机抽取50名学生的测试成绩x(单位:分,百分制)作为一个样本.
【收集数据】
调查研究小组收集到50名学生的测试成绩数据如下:60、61、62、94、73、73、85、85、87、72、63、64、70、66、74、65、67、75、76、71、94、93、84、91、76、82、83、83、92、84、80、80、82、92、91、86、77、86、88、72、70、71、93、90、81、90、74、78、81、75.
【整理数据】
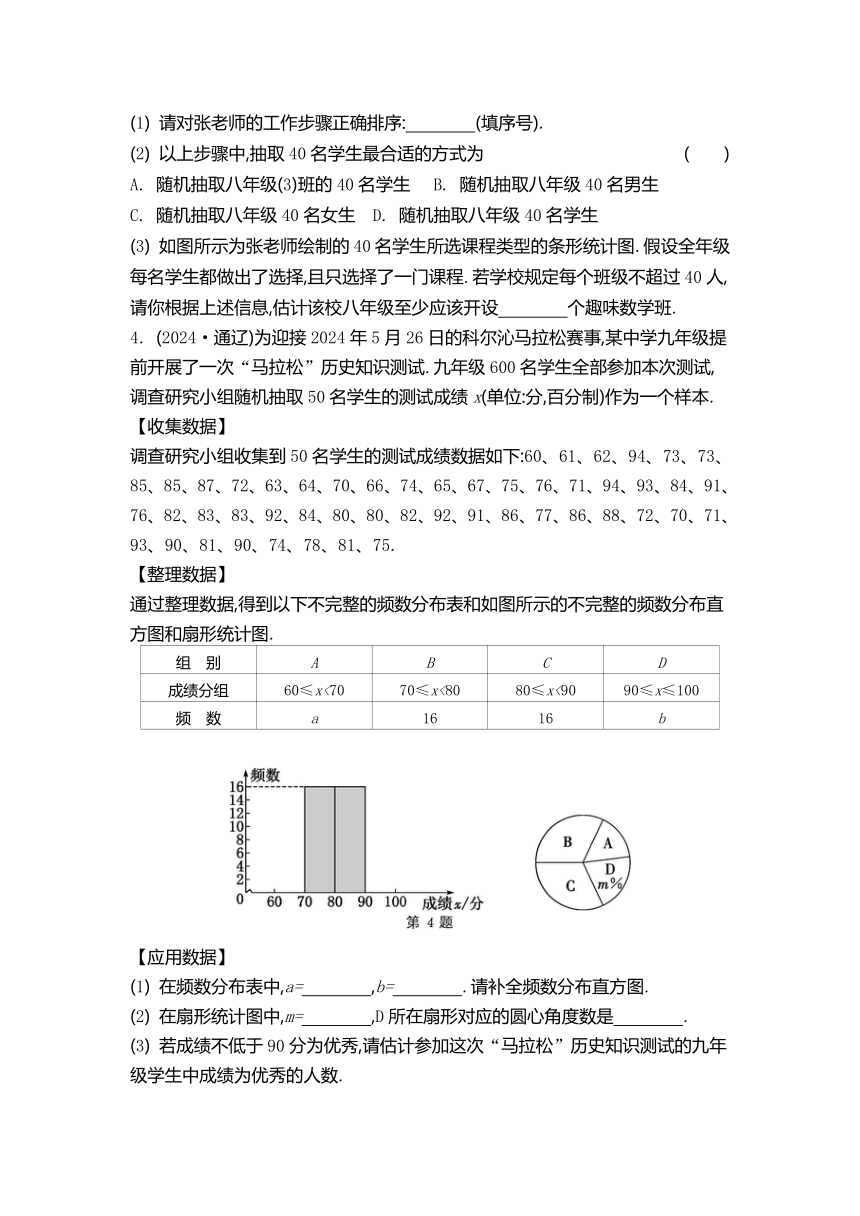
通过整理数据,得到以下不完整的频数分布表和如图所示的不完整的频数分布直方图和扇形统计图.
组 别 A B C D
成绩分组 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
频 数 a 16 16 b
【应用数据】
(1) 在频数分布表中,a= ,b= .请补全频数分布直方图.
(2) 在扇形统计图中,m= ,D所在扇形对应的圆心角度数是 .
(3) 若成绩不低于90分为优秀,请估计参加这次“马拉松”历史知识测试的九年级学生中成绩为优秀的人数.
第2课时 用样本估计总体
1. 在统计里,我们通常是从总体中抽取样本,并根据样本的某种特性 总体的相应特性.
2. 根据样本估计总体的数学思想,我们可以用样本的平均数、方差来估计总体的 ,用样本的频数分布来估计总体的 .
1.
(2023·乐山)乐山是一座著名的旅游城市,有着丰富的文旅资源.某校准备组织七年级500名学生进行研学旅行活动,政教处周老师随机抽取了其中50名学生进行研学目的地意向调查,并将调查结果制成如图所示的统计图.估计七年级愿意去“沫若故居”的学生人数为 ( )
A. 100 B. 150 C. 200 D. 400
2. (2023·河南)某林木良种繁育试验基地为全面掌握“无絮杨”品种苗的生长规律,定期对培育的1000棵该品种苗进行抽测.如图所示为某次随机抽测该品种苗的高度x(cm)的统计图,则此时该基地高度不低于300cm的“无絮杨”品种苗约有 棵.
3. (2023·自贡)某校为了解“世界读书日”主题活动开展情况,对本学期开学以来学生课外读书情况进行了随机抽样调查,所抽取的12名学生课外读书数量(单位:本)如下:2、4、5、4、3、5、3、4、1、3、2、4.
(1) 补全如图所示的学生课外读书数量条形统计图;
(2) 请直接写出本次所抽取学生课外读书数量的众数、中位数和平均数;
(3) 该校有600名学生,请根据抽样调查的结果,估计本学期开学以来课外读书数量不少于3本的学生人数.
第3题
4. (2024·浙江)某校开展科学活动.为了解学生对活动项目的喜爱情况,随机抽取部分学生进行问卷调查.调查问卷和统计结果如图所示.
关于科学活动喜爱项目的调查问卷
以下问题均为单选题,请根据实际情况填写.
问题1:在下列科学“嘉年华”项目中,你最喜爱的是 ( )
A. 科普讲座B. 科幻电影C. AI应用D. 科学魔术
如果问题1选择C,请继续回答问题2.
问题2:你更关注的AI应用是 ( )
E. 辅助学习 F. 虚拟体验 G. 智能生活 H. 其他
(1) 在本次调查中,最喜爱“AI应用”的学生中更关注“辅助学习”的有多少名
(2) 若该学校共有1200名学生,请估计该校最喜爱“科普讲座”的学生人数.
8.1 中学生的视力情况调查
第1课时 简单随机抽样
1. 总体 代表 2. 相同
1. C 2. ③ 3. (1) ①③②④ (2) D (3) 5
4. (1) 8 10 补全频数分布直方图如图所示 (2) 20 72° (3) 估计参加这次“马拉松”历史知识测试的九年级学生中成绩为优秀的人数为600×20%=120
第2课时 用样本估计总体
1. 估计 2. 平均数、方差 频数分布
1. C 2. 280
3. (1) 略 (2) 众数为4本,中位数为3.5本,平均数为本 (3) 600×=450(名).答:估计本学期开学以来课外读书数量不少于3本的学生人数为450
4. (1) 最喜爱“AI应用”的学生中更关注“辅助学习”的有80×40%=32(名) (2) 估计该校最喜爱“科普讲座”的学生人数为1200×=324
第1课时 简单随机抽样
1. 抽样调查是从总体中抽取样本进行调查,根据样本来估计 的一种调查方式.为了获得较为准确的调查结果,抽样时要注意样本的 性和广泛性.
2. 一般地,从个体总数为N的总体中抽取容量为n的样本(n
(2024·赤峰改编)下列调查中,适宜采用抽样调查的是 ( )
A. 调查某班学生的身高情况
B. 调查亚运会100m游泳决赛运动员的身体状况
C. 调查某品牌新能源汽车的最大续航里程
D. 检测“神舟十六号”飞船的零部件
2. 想要调查某大型企业员工对企业的满意度,有下列选取的调查对象:① 企业的男员工;② 企业年满40岁的员工;③ 借助企业人员名册,随机抽取四分之一的员工;④ 企业新进员工.其中,具有代表性的是 (填序号).
第3题
3. 某校拟开设四门校本课程供学生选择:A.文学鉴赏;B. 趣味数学;C. 川行历史;D. 航模科技.为了解该校八年级1000名学生对四门校本课程的选择意向,张老师做了以下工作:① 抽取40名学生作为调查对象;② 整理数据并绘制统计图;③ 收集40名学生对四门课程的选择意向的相关数据;④ 结合统计图分析数据并得出结论.
(1) 请对张老师的工作步骤正确排序: (填序号).
(2) 以上步骤中,抽取40名学生最合适的方式为 ( )
A. 随机抽取八年级(3)班的40名学生 B. 随机抽取八年级40名男生
C. 随机抽取八年级40名女生 D. 随机抽取八年级40名学生
(3) 如图所示为张老师绘制的40名学生所选课程类型的条形统计图.假设全年级每名学生都做出了选择,且只选择了一门课程.若学校规定每个班级不超过40人,请你根据上述信息,估计该校八年级至少应该开设 个趣味数学班.
4. (2024·通辽)为迎接2024年5月26日的科尔沁马拉松赛事,某中学九年级提前开展了一次“马拉松”历史知识测试.九年级600名学生全部参加本次测试,调查研究小组随机抽取50名学生的测试成绩x(单位:分,百分制)作为一个样本.
【收集数据】
调查研究小组收集到50名学生的测试成绩数据如下:60、61、62、94、73、73、85、85、87、72、63、64、70、66、74、65、67、75、76、71、94、93、84、91、76、82、83、83、92、84、80、80、82、92、91、86、77、86、88、72、70、71、93、90、81、90、74、78、81、75.
【整理数据】
通过整理数据,得到以下不完整的频数分布表和如图所示的不完整的频数分布直方图和扇形统计图.
组 别 A B C D
成绩分组 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
频 数 a 16 16 b
【应用数据】
(1) 在频数分布表中,a= ,b= .请补全频数分布直方图.
(2) 在扇形统计图中,m= ,D所在扇形对应的圆心角度数是 .
(3) 若成绩不低于90分为优秀,请估计参加这次“马拉松”历史知识测试的九年级学生中成绩为优秀的人数.
第2课时 用样本估计总体
1. 在统计里,我们通常是从总体中抽取样本,并根据样本的某种特性 总体的相应特性.
2. 根据样本估计总体的数学思想,我们可以用样本的平均数、方差来估计总体的 ,用样本的频数分布来估计总体的 .
1.
(2023·乐山)乐山是一座著名的旅游城市,有着丰富的文旅资源.某校准备组织七年级500名学生进行研学旅行活动,政教处周老师随机抽取了其中50名学生进行研学目的地意向调查,并将调查结果制成如图所示的统计图.估计七年级愿意去“沫若故居”的学生人数为 ( )
A. 100 B. 150 C. 200 D. 400
2. (2023·河南)某林木良种繁育试验基地为全面掌握“无絮杨”品种苗的生长规律,定期对培育的1000棵该品种苗进行抽测.如图所示为某次随机抽测该品种苗的高度x(cm)的统计图,则此时该基地高度不低于300cm的“无絮杨”品种苗约有 棵.
3. (2023·自贡)某校为了解“世界读书日”主题活动开展情况,对本学期开学以来学生课外读书情况进行了随机抽样调查,所抽取的12名学生课外读书数量(单位:本)如下:2、4、5、4、3、5、3、4、1、3、2、4.
(1) 补全如图所示的学生课外读书数量条形统计图;
(2) 请直接写出本次所抽取学生课外读书数量的众数、中位数和平均数;
(3) 该校有600名学生,请根据抽样调查的结果,估计本学期开学以来课外读书数量不少于3本的学生人数.
第3题
4. (2024·浙江)某校开展科学活动.为了解学生对活动项目的喜爱情况,随机抽取部分学生进行问卷调查.调查问卷和统计结果如图所示.
关于科学活动喜爱项目的调查问卷
以下问题均为单选题,请根据实际情况填写.
问题1:在下列科学“嘉年华”项目中,你最喜爱的是 ( )
A. 科普讲座B. 科幻电影C. AI应用D. 科学魔术
如果问题1选择C,请继续回答问题2.
问题2:你更关注的AI应用是 ( )
E. 辅助学习 F. 虚拟体验 G. 智能生活 H. 其他
(1) 在本次调查中,最喜爱“AI应用”的学生中更关注“辅助学习”的有多少名
(2) 若该学校共有1200名学生,请估计该校最喜爱“科普讲座”的学生人数.
8.1 中学生的视力情况调查
第1课时 简单随机抽样
1. 总体 代表 2. 相同
1. C 2. ③ 3. (1) ①③②④ (2) D (3) 5
4. (1) 8 10 补全频数分布直方图如图所示 (2) 20 72° (3) 估计参加这次“马拉松”历史知识测试的九年级学生中成绩为优秀的人数为600×20%=120
第2课时 用样本估计总体
1. 估计 2. 平均数、方差 频数分布
1. C 2. 280
3. (1) 略 (2) 众数为4本,中位数为3.5本,平均数为本 (3) 600×=450(名).答:估计本学期开学以来课外读书数量不少于3本的学生人数为450
4. (1) 最喜爱“AI应用”的学生中更关注“辅助学习”的有80×40%=32(名) (2) 估计该校最喜爱“科普讲座”的学生人数为1200×=324
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
