6.4 探索三角形相似的条件(5课时,含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 6.4 探索三角形相似的条件(5课时,含答案) 2024-2025学年数学苏科版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 489.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览



文档简介
6.4 探索三角形相似的条件
第1课时 平行线分线段成比例及平行线截三角形相似
1.
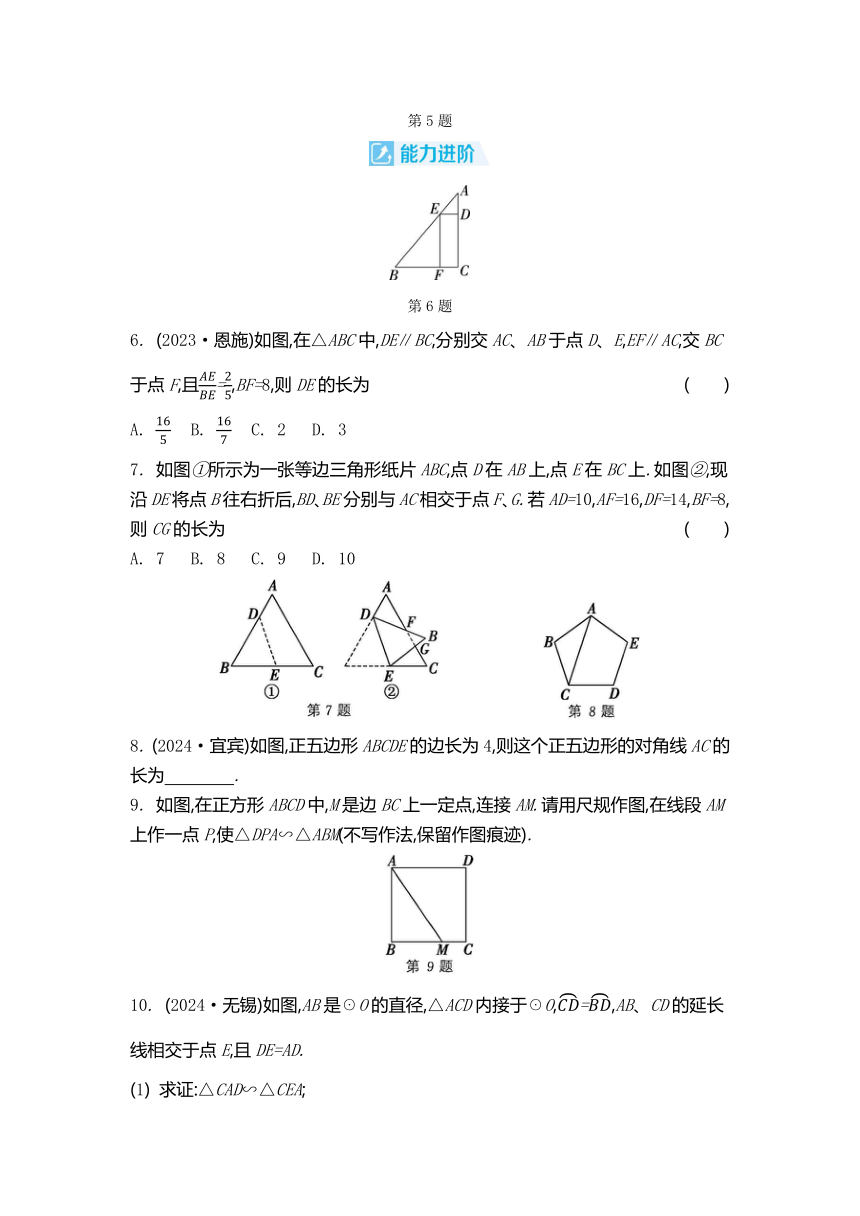
如图,AD∥BE∥CF,直线l1、l2分别截AD、BE、CF于点A、B、C和点D、E、F.下列结论正确的是 ( )
A. = B. = C. = D. =
2. 如图,DE∥FG∥BC.若DB=4FB,则EG与GC的关系是 ( )
A. =4 B. =3 C. = D. =2
3. (2023·北京)如图,直线AD、BC交于点O,AB∥EF∥CD.若AO=2,OF=1,FD=2,则的值为 .
4. 如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为 .
5. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D,过点D作☉O的切线,交BC于点E,连接OE.求证:
(1) △DBE是等腰三角形;
(2) △COE∽△CAB.
第5题
第6题6. 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,M为边BC上一点(不与点B、C重合),连接AM交DE于点N,则下列结论正确的是 ( )
A. = B. =
C. = D. =
7. (2024·陕西)如图,正方形CEFG的顶点G在正方形ABCD的边CD上,AF与DC交于点H.若AB=6,CE=2,则DH的长为 ( )
A. 2 B. 3 C. D.
8. 如图,AD是△ABC的中线,AE=EF=FC,BE交AD于点G,连接DF,则的值为 .
9. (2023·岳阳)如图,在☉O中,AB为直径,BD为弦,C为的中点,连接AC,交BD于点F,以C为切点的切线与AB的延长线交于点E,连接CD.若=,则的值为 .
10. 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6.
(1) 直接指出图中所有的相似三角形;
(2) 求DE的长.
第10题
11. 如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,交BC于点E.若BF∶FD=3∶1,AB+BE=3,求△ABC的周长.
第11题
第2课时 用两角的关系判定三角形相似
1.
如图,D、E、F、G四点分别在△ABC的三边上,其中DG与EF相交于点H.若∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列三角形相似的是 ( )
A. △BDG和△CEF B. △ABC和△EFC C. △ABC和△BDG D. △FGH和△ABC
2. 有下列图形:① 两个等边三角形;② 两个顶角为40°的等腰三角形;③ 两个底角为40°的等腰三角形.其中,一定相似的有 ( )
A. 0组 B. 1组 C. 2组 D. 3组
3. (2023·大庆)如图,点N在矩形纸片ABCD的边AD上,现将矩形折叠,折痕为BN,点A的对应点为M.若点M恰好落在边DC上,则图中与△NDM一定相似的三角形是 .
4. 如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为 .
5. (2024·德阳)如图,在菱形ABCD中,∠ABC=60°,对角线AC与BD相交于点O,F为BC的中点,连接AF与BD相交于点E,连接CE并延长,交AB于点G.求证:△BEF∽△BCO.
第5题
第6题
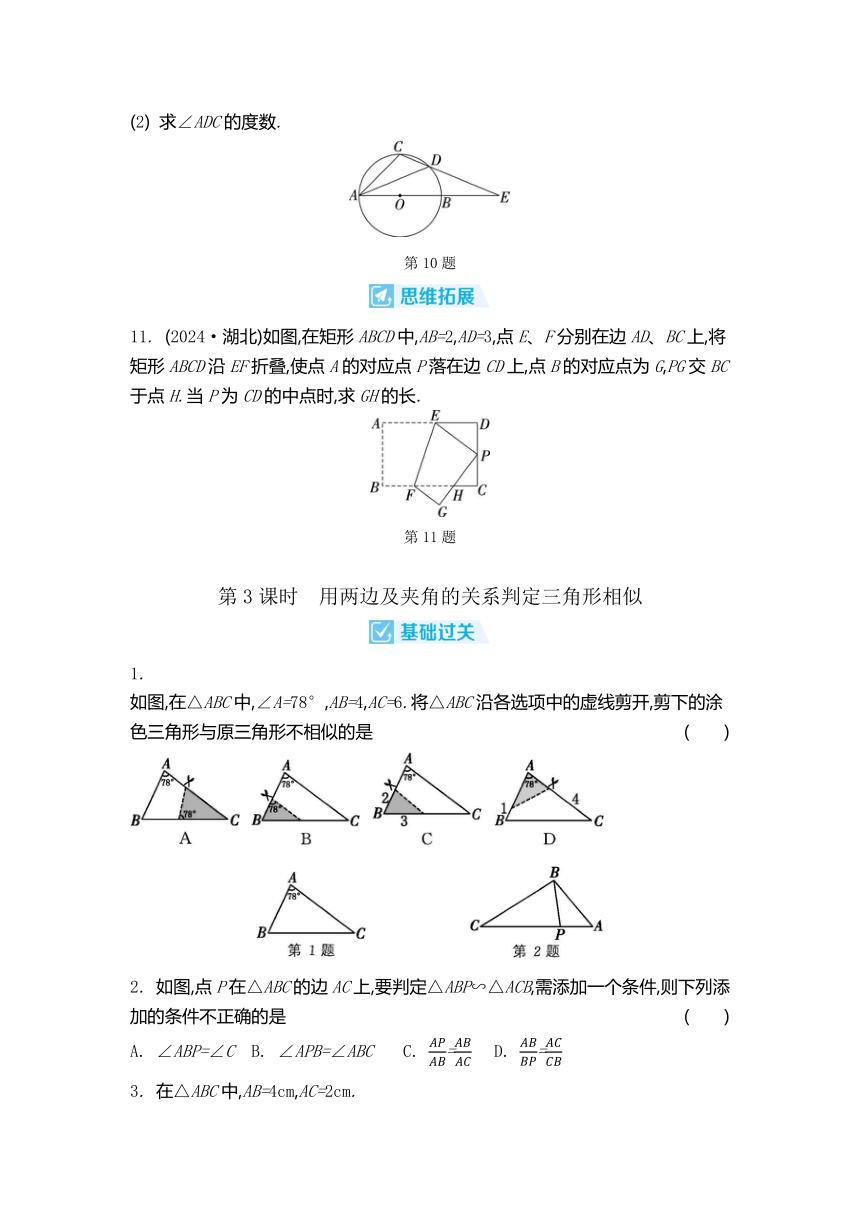
6. (2023·恩施)如图,在△ABC中,DE∥BC,分别交AC、AB于点D、E,EF∥AC,交BC于点F,且=,BF=8,则DE的长为 ( )
A. B. C. 2 D. 3
7. 如图①所示为一张等边三角形纸片ABC,点D在AB上,点E在BC上.如图②,现沿DE将点B往右折后,BD、BE分别与AC相交于点F、G.若AD=10,AF=16,DF=14,BF=8,则CG的长为 ( )
A. 7 B. 8 C. 9 D. 10
8. (2024·宜宾)如图,正五边形ABCDE的边长为4,则这个正五边形的对角线AC的长为 .
9. 如图,在正方形ABCD中,M是边BC上一定点,连接AM.请用尺规作图,在线段AM上作一点P,使△DPA∽△ABM(不写作法,保留作图痕迹).
10. (2024·无锡)如图,AB是☉O的直径,△ACD内接于☉O,=,AB、CD的延长线相交于点E,且DE=AD.
(1) 求证:△CAD∽△CEA;
(2) 求∠ADC的度数.
第10题
11. (2024·湖北)如图,在矩形ABCD中,AB=2,AD=3,点E、F分别在边AD、BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为G,PG交BC于点H.当P为CD的中点时,求GH的长.
第11题
第3课时 用两边及夹角的关系判定三角形相似
1.
如图,在△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿各选项中的虚线剪开,剪下的涂色三角形与原三角形不相似的是 ( )
2. 如图,点P在△ABC的边AC上,要判定△ABP∽△ACB,需添加一个条件,则下列添加的条件不正确的是 ( )
A. ∠ABP=∠C B. ∠APB=∠ABC C. = D. =
3. 在△ABC中,AB=4cm,AC=2cm.
(1) 在AB上取一点D,连接CD.当AD= cm时,△ACD∽△ABC.
(2) 在AC的延长线上取一点E,连接BE.当CE= cm时,△AEB∽△ABC.
4. 如图,线段AB是☉O的直径,延长AB至点C,使BC=OB,E是线段OB的中点,DE⊥AB,交☉O于点D,P是☉O上一动点(不与点A、B重合),连接CD、PE、PC.
(1) 求证:CD是☉O的切线;
(2) 求的值.
第4题
第5题
5. 如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内径AB.若OA∶OC=OB∶OD=3,且量得CD=3cm,则零件的厚度为 ( )
A. 0.3cm B. 0.5cm
C. 0.7cm D. 1cm
6. (2024·威海)如图,在 ABCD中,对角线AC、BD交于点O,点E在BC上,点F在CD上,连接AE、AF、EF,EF交AC于点G.下列结论错误的是 ( )
A. 若=,则EF∥BD
B. 若AE⊥BC,AF⊥CD,AE=AF,则EF∥BD
C. 若EF∥BD,CE=CF,则∠EAC=∠FAC
D. 若AB=AD,AE=AF,则EF∥BD
7. 如图,在△ABC中,D为BC上一点,BC=AB=3BD,则AD∶AC的值为 .
8. (2023·徐州)如图,在△ABC中,∠B=90°,∠A=30°,BC=2,D为AB的中点.若点E在边AC上,且=,则AE的长为 .
9. 如图,点C、D在线段AB上,△PCD是等边三角形.
(1) 当AC、CD、DB满足怎样的关系时,△ACP∽△PDB 请说明理由.
(2) 当△ACP∽△PDB时,求∠APB的度数.
第9题
10. (2024·武汉改编)如图,在矩形ABCD中,AB=3cm,BC=6cm.某一时刻,动点M从点A出发,沿AB方向以1cm/s的速度向点B运动;同时动点N从点D出发,沿DA方向以2cm/s的速度向点A运动.当运动时间为多少秒时,以A、M、N为顶点的三角形与△ACD相似
第10题
第4课时 用三边的关系判定三角形相似
1.
若△ABC的每条边长增加各自的10%得到△A'B'C',则∠B'的度数与其对应角∠B的度数相比,下列说法正确的是 ( )
A. 增加了10% B. 减少了10% C. 增加了(1+10%) D. 没有改变
2. 如图,每个小正方形的边长均为1,则下列图形中,三角形(涂色部分)与△A1B1C1相似的是 ( )
3. 有下列各组三角形:① 在△ABC中,AB=8,AC=4,∠A=105°,在△A'B'C'中,A'B'=16,B'C'=8,∠A'=100°;② 在△ABC中,AB=18,BC=20,CA=35,在△A'B'C'中,A'B'=36,B'C'=40,C'A'=70;③ 在△ABC和△A'B'C'中,=,∠C=∠C'.其中,两个三角形相似的是 (填序号).
4. 在△ABC中,AB=4,BC=5,CA=6.
(1) 如果DE=10,那么当EF= ,FD= 时,△DEF∽△ABC;
(2) 如果DE=10,那么当EF= ,FD= 时,△FDE∽△ABC.
5. 如图,O为△ABC内任意一点,A'、B'、C'分别是线段OA、OB、OC的中点,△A'B'C'与△ABC相似吗 请说明理由.
第5题
6. 一个三角形木架的三边长分别为75cm、100cm、120cm,现要做一个与其相似的三角形木架,而只有长为60cm和120cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另外两边(这根允许有余料),则不同的截法有 ( )
A. 一种 B. 两种 C. 三种 D. 四种
7. 如图,在正方形网格中,若使△ABC与△PBD相似,则点P应在 ( )
A. 点P1处 B. 点P2处 C. 点P3处 D. 点P4处
8. 如图,方格纸中每个小正方形的边长均为1,△ABC和△DEF的顶点都在方格纸的格点上.P1、P2、P3、P4、P5、D、E、F是△DEF边上的格点,在这些格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似,则满足条件的三角形共有 个.
9. 如图,在由边长为1的25个小正方形组成的正方形网格中有一个△ABC,若在网格中画一个与△ABC相似的、面积最大的△A'B'C',且其顶点在小正方形的顶点上,则它的最大面积S为 .
10. 如图,△ABC各顶点的坐标分别为A(3,0)、B(0,4)、C(4,2),过点C作CD⊥x轴,垂足为D.
(1) △AOB与△ADC是否相似 请说明理由.
(2) △ACB与△ADC是否相似 请说明理由.
第10题
11. 如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,=,且==.求证:△ABC∽△A'B'C'.
第11题
第5课时 与判定三角形相似有关的应用及三角形的重心
1.
如图,☉O是△ABC的外接圆,AD平分∠BAC,交☉O于点D,交BC于点E.若AD=5,BD=2,则DE的长为 ( )
A. B. C. D.
2. 若三角形的重心在它的一条高上,则这个三角形一定是 ( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 等腰直角三角形
3. 如图,在Rt△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD的长为 .
4. 如图,半圆O与四边形ABCD的边AD、AB、BC都相切,切点分别为D、E、C,半径OC=1,则AE·BE的值为 .
5. 在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上.当AE的长为 时,以A、D、E为顶点的三角形与△ABC相似.
6. 如图,AB、AC是☉O的两条弦,且AB=AC,D是AO的延长线上一点,连接BD并延长,交☉O于点E,连接CD并延长,交☉O于点F.
(1) 求证:BD=CD;
(2) 如果AB2=AO·AD,求证:四边形ABDC是菱形.
第6题
第7题7. 如图,图中的相似三角形共有 ( )
A. 5对
B. 4对
C. 3对
D. 2对
8. 如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交DC于点G,交AD的延长线于点E.若AB=12,BM=5,则DE的长为 ( )
A. 18 B. C. D.
9. (2024·眉山)如图,△ABC内接于☉O,圆点O在AB上,AD平分∠BAC交☉O于点D,连接BD.若AB=10,BD=2,则BC的长为 .
10. 如图,在平面直角坐标系中,有两点A(4,0)、B(0,2).如果点C在x轴上(不与点A重合),那么当点C的坐标为 时,以B、O、C为顶点的三角形与△AOB相似.
11. 如图,在△ABC中,D是BC的中点,E为△ABC内一点.∠ABE=∠C,∠BAE=∠CAD,连接DE.求证:DE∥AC.
第11题
12. 如图,点P是△ABC的重心,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.求证:a2+b2=5c2.
第12题
6.4 探索三角形相似的条件
第1课时 平行线分线段成比例
及平行线截三角形相似
1. C 2. B 3. 4. 4
5. (1) 连接OD.∵ DE是☉O的切线,∴ OD⊥DE,即∠ODE=90°.∴ ∠ADO+∠BDE=90°.∵ 在△ABC中,∠ACB=90°,∴ ∠A+∠B=90°.∵ OA=OD,∴ ∠A=∠ADO.∴ ∠BDE=∠B.∴ ED=EB.∴ △DBE是等腰三角形 (2) ∵ ∠ACB=90°,AC是☉O的直径,∴ CB是☉O的切线.∵ DE是☉O的切线,∴ ED=EC.∵ ED=EB,∴ EC=EB.∵ OA=OC,∴ OE∥AB.∴ △COE∽△CAB
6. D 7. B 8.
9. 解析:连接OC.根据垂径定理,易得OC⊥BD.由切线的性质,得OC⊥EC.∴ EC∥BD.利用平行线分线段成比例,得==.设EB=x,则AB=3x.∴ OB=OC=AB=x.∴ EO=EB+OB=x.在Rt△OCE中,根据勾股定理,可得EC==2x.∴ ==.
10. (1) △ADE∽△ABC;△EFC∽△ABC;△ADE∽△EFC (2) ∵ DE∥BC,∴ ∠ADE=∠B.∵ ∠ADE=∠EFC,∴ ∠B=∠EFC.∴ AB∥EF,即BD∥EF.∴ 四边形BDEF为平行四边形.∴ DE=BF.∵ DE∥BC,AD∶BD=5∶3,∴ ==.∵ AB∥EF,∴ ==.∵ CF=6,∴ BF=10.∴ DE=10
11. 如图,过点F作FM⊥AB于点M,FN⊥AC于点N,过点D作DT∥AE,交BC于点T.∵ AE平分∠BAC,FM⊥AB,FN⊥AC,∴ FM=FN.∵ BF∶FD=3∶1,∴ S△ABF∶S△ADF=3∶1.∴ AB=3AD.∵ D是AC的中点,∴ AD=CD.∴ AB=AC.∵ DT∥AE,∴ =.∴ ET=CT.∵ DT∥AE,即FE∥DT,∴ BF∶FD=BE∶ET=3∶1.∴ BE=CE.∴ AB+BE=(AC+CE).∵ AB+BE=3,∴ AC+CE=2.∴ △ABC的周长为AB+AC+BC=(AB+BE)+(AC+CE)=3+2=5
第2课时 用两角的关系判定三角形相似
1. B 2. D 3. △MCB 4.
5. ∵ 四边形ABCD是菱形,∴ AB=BC,AC⊥BD.∴ ∠BOC=90°.∵ ∠ABC=60°,∴ △ABC是等边三角形.∴ AB=AC.∵ F为BC的中点,∴ AF⊥BC.∴ ∠BFE=90°.∴ ∠BFE=∠BOC.∵ ∠EBF=∠CBO,∴ △BEF∽△BCO
6. A 7. C
8. 2+2 解析:连接BE交AC于点O,证△ABO∽△ACB,得=,解得AC=2+2或AC=-2+2(不合题意,舍去).
9. 如图所示
10. (1) ∵ =,∴ ∠CAD=∠DAB.∵ DE=AD,∴ ∠DAB=∠E.∴ ∠CAD=∠E.又∵ ∠C=∠C,∴ △CAD∽△CEA (2) 连接BD.∵ AB是☉O的直径,∴ ∠ADB=90°.设∠CAD=∠DAB=α,则∠EAC=2α.由(1),知△CAD∽△CEA,∴ ∠ADC=∠EAC=2α.∵ 四边形ABDC是圆内接四边形,∴ ∠CAB+∠CDB=180°,即2α+2α+90°=180°,解得α=22.5°.∴ ∠ADC=2α=2×22.5°=45°
11. ∵ 四边形ABCD是矩形,∴ CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°.∴ ∠DEP+∠DPE=90°.∵ P为CD的中点,∴ DP=PC=×2=1.由折叠,知EP=AE,∠EPH=∠A=90°,PG=AB=2.∴ ∠DPE+∠CPH=90°.∴ ∠DEP=∠CPH.∴ △EDP∽△PCH.∴ =.设EP=AE=x,则ED=3-x.∵ 在Rt△EDP中,EP2=ED2+DP2,∴ x2=(3-x)2+12,解得x=.∴ EP=AE=,ED=.∴ =.∴ PH=.∴ GH=PG-PH=
第3课时 用两边及夹角的关系判定三角形相似
1. C 2. D 3. (1) 1 (2) 6
4. (1) 连接OD、DB.∵ E是线段OB的中点,DE⊥AB,∴ DE垂直平分OB.∴ DB=OD.∵ 在☉O中,OD=OB,∴ DB=OD=OB.∴ △ODB是等边三角形.∴ ∠BDO=∠DBO=60°.∵ BC=OB=DB,∴ ∠BCD=∠BDC=∠DBO=30°.∴ ∠ODC=∠BDO+∠BDC=90°,即OD⊥CD.∵ OD是☉O的半径,∴ CD是☉O的切线 (2) 连接OP.由题意,得OP=OB=BC=2OE,OC=OB+BC.∴ ==.又∵ ∠POE=∠COP,∴ △OEP∽△OPC.∴ ==
5. B 6. D 7. 8. 1或2
9. (1) 当AC、CD、DB满足CD2=AC·DB时,△ACP∽△PDB 理由:∵ △PCD是等边三角形,∴ ∠PCD=∠PDC=60°,PD=CD=CP.∴ ∠ACP=∠PDB=120°.∴ 当=,即=时,△ACP∽△PDB.∴ 当CD2=AC·DB时,△ACP∽△PDB. (2) ∵ △ACP∽△PDB,∴ ∠A=∠BPD.∵ △PCD是等边三角形,∴ ∠CPD=∠DCP=60°.∴ ∠APB=∠APC+∠CPD+∠BPD=∠APC+∠CPD+∠A=∠DCP+∠CPD=120°
10. 根据题意,得AD=BC=6cm,CD=AB=3cm,∠D=∠MAN=90°.设运动时间为ts,则MA=tcm,NA=(6-2t)cm.分两种情况讨论:① 当△ACD∽△MNA时,=,∴ =,解得t=2.4.② 当△ACD∽△NMA时,=,∴ =,解得t=1.5.综上所述,当运动时间为2.4s或1.5s时,以A、M、N为顶点的三角形与△ACD相似
第4课时 用三边的关系判定三角形相似
1. D 2. B 3. ② 4. (1) 15 (2) 12 8
5. 相似 理由:∵ A'、B'分别是线段OA、OB的中点,∴ A'B'是△AOB的中位线.∴ =.同理,可得=,=.∴ ==.∴ △A'B'C'∽△ABC.
6. B 解析:∵ 长为120cm的木条与三角形木架的最长边相等,∴ 长为120cm的木条不能作为一边.设从长为120 cm的木条上截下的两段分别长为x cm、y cm(x7. C 8. 8 9. 5
10. (1) 不相似 理由:∵ CD⊥x轴,∴ ∠ADC=90°.∵ ∠AOB=90°,∴ ∠AOB=∠ADC.∵ A(3,0)、B(0,4)、C(4,2),∴ OA=3,OB=4,OD=4,DC=2.∴ DA=OD-OA=1.∴ ==2,==3.∴ ≠.∴ △AOB与△ADC不相似. (2) 相似 理由:在Rt△AOB中,AB==5,在Rt△ADC中,AC==.过点C作CH⊥OB于点H,则易得四边形ODCH为矩形.∴ CH=OD=4,OH=CD=2.∴ BH=4-2=2.在Rt△BHC中,BC==2.∴ ==,==,==.∴ ==.∴ △ACB∽△ADC.
11. ∵ =,∴ =.∵ ==,∴ ==.∴ △ADC∽△A'D'C'.∴ ∠A=∠A'.∵ =,∴ △ABC∽△A'B'C'
第5课时 与判定三角形相似有关的应用
及三角形的重心
1. D 2. A 3. 4. 1 5. 或
6. (1) 连接BC、OB、OC.∵ AB=AC,∴ 点A在BC的垂直平分线上.∵ OB=OC,∴ 点O在BC的垂直平分线上.∴ AO垂直平分BC.∴ BD=CD (2) ∵ AB2=AO·AD,∴ =.∵ ∠BAO=∠DAB,∴ △ABO∽△ADB.∴ ∠OBA=∠BDA.∵ OB=OA,∴ ∠OBA=∠OAB.∴ ∠OAB=∠BDA.∴ AB=BD.∵ AB=AC,BD=CD,∴ AB=AC=BD=CD.∴ 四边形ABDC是菱形
7. B 8. B
9. 8 解析:延长AC、BD交于点E.在Rt△ADB中,根据勾股定理求出AD=4.先证△BAD≌△EAD,得BD=DE=2.再证△BEC∽△ABD,得=,解得BC=8.
10. (-4,0)或(1,0)或(-1,0)
11. 如图,延长BE,交AC于点F.∵ ∠ABE=∠C,∠BAE=∠CAD,∴ △ABE∽△ACD.∴ =.∵ ∠BAE=∠CAD,∴ ∠BAE+∠DAE=∠CAD+∠DAE,即∠BAD=∠FAE.∵ ∠AEF=∠ABE+∠BAE,∠ADB=∠CAD+∠C,∴ ∠AEF=∠ADB.∴ △EAF∽△DAB.∴ =.∴ =.∵ D是BC的中点,∴ CD=BD.∴ BE=EF.∴ DE是△BCF的中位线.∴ DE∥AC
12. 连接EF,设PF=m,PE=n.∵ 点P是△ABC的重心,∴ E、F分别为AC、BC的中点.∴ EF为△ABC的中位线.∴ EF∥AB,EF=AB,AE=AC,BF=BC.∵ BC=a,AC=b,AB=c,∴ AE=b,BF=a,EF=c.∵ EF∥AB,∴ ∠EFP=∠BAP,∠FEP=∠ABP.∴ △EFP∽△BAP.∴ ===,即==.∴ PB=2n,PA=2m.∵ AF⊥BE,∴ 在Rt△AEP中,由勾股定理,得PE2+PA2=AE2,得n2+4m2=b2①;在Rt△BFP中,由勾股定理,得PF2+PB2=BF2,得m2+4n2=a2②.①+②,得5(n2+m2)=(a2+b2).在Rt△EFP中,由勾股定理,得PE2+PF2=EF2,得n2+m2=c2.∴ 5×c2=(a2+b2),即a2+b2=5c2
第1课时 平行线分线段成比例及平行线截三角形相似
1.
如图,AD∥BE∥CF,直线l1、l2分别截AD、BE、CF于点A、B、C和点D、E、F.下列结论正确的是 ( )
A. = B. = C. = D. =
2. 如图,DE∥FG∥BC.若DB=4FB,则EG与GC的关系是 ( )
A. =4 B. =3 C. = D. =2
3. (2023·北京)如图,直线AD、BC交于点O,AB∥EF∥CD.若AO=2,OF=1,FD=2,则的值为 .
4. 如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为 .
5. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D,过点D作☉O的切线,交BC于点E,连接OE.求证:
(1) △DBE是等腰三角形;
(2) △COE∽△CAB.
第5题
第6题6. 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,M为边BC上一点(不与点B、C重合),连接AM交DE于点N,则下列结论正确的是 ( )
A. = B. =
C. = D. =
7. (2024·陕西)如图,正方形CEFG的顶点G在正方形ABCD的边CD上,AF与DC交于点H.若AB=6,CE=2,则DH的长为 ( )
A. 2 B. 3 C. D.
8. 如图,AD是△ABC的中线,AE=EF=FC,BE交AD于点G,连接DF,则的值为 .
9. (2023·岳阳)如图,在☉O中,AB为直径,BD为弦,C为的中点,连接AC,交BD于点F,以C为切点的切线与AB的延长线交于点E,连接CD.若=,则的值为 .
10. 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6.
(1) 直接指出图中所有的相似三角形;
(2) 求DE的长.
第10题
11. 如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,交BC于点E.若BF∶FD=3∶1,AB+BE=3,求△ABC的周长.
第11题
第2课时 用两角的关系判定三角形相似
1.
如图,D、E、F、G四点分别在△ABC的三边上,其中DG与EF相交于点H.若∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列三角形相似的是 ( )
A. △BDG和△CEF B. △ABC和△EFC C. △ABC和△BDG D. △FGH和△ABC
2. 有下列图形:① 两个等边三角形;② 两个顶角为40°的等腰三角形;③ 两个底角为40°的等腰三角形.其中,一定相似的有 ( )
A. 0组 B. 1组 C. 2组 D. 3组
3. (2023·大庆)如图,点N在矩形纸片ABCD的边AD上,现将矩形折叠,折痕为BN,点A的对应点为M.若点M恰好落在边DC上,则图中与△NDM一定相似的三角形是 .
4. 如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为 .
5. (2024·德阳)如图,在菱形ABCD中,∠ABC=60°,对角线AC与BD相交于点O,F为BC的中点,连接AF与BD相交于点E,连接CE并延长,交AB于点G.求证:△BEF∽△BCO.
第5题
第6题
6. (2023·恩施)如图,在△ABC中,DE∥BC,分别交AC、AB于点D、E,EF∥AC,交BC于点F,且=,BF=8,则DE的长为 ( )
A. B. C. 2 D. 3
7. 如图①所示为一张等边三角形纸片ABC,点D在AB上,点E在BC上.如图②,现沿DE将点B往右折后,BD、BE分别与AC相交于点F、G.若AD=10,AF=16,DF=14,BF=8,则CG的长为 ( )
A. 7 B. 8 C. 9 D. 10
8. (2024·宜宾)如图,正五边形ABCDE的边长为4,则这个正五边形的对角线AC的长为 .
9. 如图,在正方形ABCD中,M是边BC上一定点,连接AM.请用尺规作图,在线段AM上作一点P,使△DPA∽△ABM(不写作法,保留作图痕迹).
10. (2024·无锡)如图,AB是☉O的直径,△ACD内接于☉O,=,AB、CD的延长线相交于点E,且DE=AD.
(1) 求证:△CAD∽△CEA;
(2) 求∠ADC的度数.
第10题
11. (2024·湖北)如图,在矩形ABCD中,AB=2,AD=3,点E、F分别在边AD、BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为G,PG交BC于点H.当P为CD的中点时,求GH的长.
第11题
第3课时 用两边及夹角的关系判定三角形相似
1.
如图,在△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿各选项中的虚线剪开,剪下的涂色三角形与原三角形不相似的是 ( )
2. 如图,点P在△ABC的边AC上,要判定△ABP∽△ACB,需添加一个条件,则下列添加的条件不正确的是 ( )
A. ∠ABP=∠C B. ∠APB=∠ABC C. = D. =
3. 在△ABC中,AB=4cm,AC=2cm.
(1) 在AB上取一点D,连接CD.当AD= cm时,△ACD∽△ABC.
(2) 在AC的延长线上取一点E,连接BE.当CE= cm时,△AEB∽△ABC.
4. 如图,线段AB是☉O的直径,延长AB至点C,使BC=OB,E是线段OB的中点,DE⊥AB,交☉O于点D,P是☉O上一动点(不与点A、B重合),连接CD、PE、PC.
(1) 求证:CD是☉O的切线;
(2) 求的值.
第4题
第5题
5. 如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内径AB.若OA∶OC=OB∶OD=3,且量得CD=3cm,则零件的厚度为 ( )
A. 0.3cm B. 0.5cm
C. 0.7cm D. 1cm
6. (2024·威海)如图,在 ABCD中,对角线AC、BD交于点O,点E在BC上,点F在CD上,连接AE、AF、EF,EF交AC于点G.下列结论错误的是 ( )
A. 若=,则EF∥BD
B. 若AE⊥BC,AF⊥CD,AE=AF,则EF∥BD
C. 若EF∥BD,CE=CF,则∠EAC=∠FAC
D. 若AB=AD,AE=AF,则EF∥BD
7. 如图,在△ABC中,D为BC上一点,BC=AB=3BD,则AD∶AC的值为 .
8. (2023·徐州)如图,在△ABC中,∠B=90°,∠A=30°,BC=2,D为AB的中点.若点E在边AC上,且=,则AE的长为 .
9. 如图,点C、D在线段AB上,△PCD是等边三角形.
(1) 当AC、CD、DB满足怎样的关系时,△ACP∽△PDB 请说明理由.
(2) 当△ACP∽△PDB时,求∠APB的度数.
第9题
10. (2024·武汉改编)如图,在矩形ABCD中,AB=3cm,BC=6cm.某一时刻,动点M从点A出发,沿AB方向以1cm/s的速度向点B运动;同时动点N从点D出发,沿DA方向以2cm/s的速度向点A运动.当运动时间为多少秒时,以A、M、N为顶点的三角形与△ACD相似
第10题
第4课时 用三边的关系判定三角形相似
1.
若△ABC的每条边长增加各自的10%得到△A'B'C',则∠B'的度数与其对应角∠B的度数相比,下列说法正确的是 ( )
A. 增加了10% B. 减少了10% C. 增加了(1+10%) D. 没有改变
2. 如图,每个小正方形的边长均为1,则下列图形中,三角形(涂色部分)与△A1B1C1相似的是 ( )
3. 有下列各组三角形:① 在△ABC中,AB=8,AC=4,∠A=105°,在△A'B'C'中,A'B'=16,B'C'=8,∠A'=100°;② 在△ABC中,AB=18,BC=20,CA=35,在△A'B'C'中,A'B'=36,B'C'=40,C'A'=70;③ 在△ABC和△A'B'C'中,=,∠C=∠C'.其中,两个三角形相似的是 (填序号).
4. 在△ABC中,AB=4,BC=5,CA=6.
(1) 如果DE=10,那么当EF= ,FD= 时,△DEF∽△ABC;
(2) 如果DE=10,那么当EF= ,FD= 时,△FDE∽△ABC.
5. 如图,O为△ABC内任意一点,A'、B'、C'分别是线段OA、OB、OC的中点,△A'B'C'与△ABC相似吗 请说明理由.
第5题
6. 一个三角形木架的三边长分别为75cm、100cm、120cm,现要做一个与其相似的三角形木架,而只有长为60cm和120cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另外两边(这根允许有余料),则不同的截法有 ( )
A. 一种 B. 两种 C. 三种 D. 四种
7. 如图,在正方形网格中,若使△ABC与△PBD相似,则点P应在 ( )
A. 点P1处 B. 点P2处 C. 点P3处 D. 点P4处
8. 如图,方格纸中每个小正方形的边长均为1,△ABC和△DEF的顶点都在方格纸的格点上.P1、P2、P3、P4、P5、D、E、F是△DEF边上的格点,在这些格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似,则满足条件的三角形共有 个.
9. 如图,在由边长为1的25个小正方形组成的正方形网格中有一个△ABC,若在网格中画一个与△ABC相似的、面积最大的△A'B'C',且其顶点在小正方形的顶点上,则它的最大面积S为 .
10. 如图,△ABC各顶点的坐标分别为A(3,0)、B(0,4)、C(4,2),过点C作CD⊥x轴,垂足为D.
(1) △AOB与△ADC是否相似 请说明理由.
(2) △ACB与△ADC是否相似 请说明理由.
第10题
11. 如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,=,且==.求证:△ABC∽△A'B'C'.
第11题
第5课时 与判定三角形相似有关的应用及三角形的重心
1.
如图,☉O是△ABC的外接圆,AD平分∠BAC,交☉O于点D,交BC于点E.若AD=5,BD=2,则DE的长为 ( )
A. B. C. D.
2. 若三角形的重心在它的一条高上,则这个三角形一定是 ( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 等腰直角三角形
3. 如图,在Rt△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD的长为 .
4. 如图,半圆O与四边形ABCD的边AD、AB、BC都相切,切点分别为D、E、C,半径OC=1,则AE·BE的值为 .
5. 在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上.当AE的长为 时,以A、D、E为顶点的三角形与△ABC相似.
6. 如图,AB、AC是☉O的两条弦,且AB=AC,D是AO的延长线上一点,连接BD并延长,交☉O于点E,连接CD并延长,交☉O于点F.
(1) 求证:BD=CD;
(2) 如果AB2=AO·AD,求证:四边形ABDC是菱形.
第6题
第7题7. 如图,图中的相似三角形共有 ( )
A. 5对
B. 4对
C. 3对
D. 2对
8. 如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交DC于点G,交AD的延长线于点E.若AB=12,BM=5,则DE的长为 ( )
A. 18 B. C. D.
9. (2024·眉山)如图,△ABC内接于☉O,圆点O在AB上,AD平分∠BAC交☉O于点D,连接BD.若AB=10,BD=2,则BC的长为 .
10. 如图,在平面直角坐标系中,有两点A(4,0)、B(0,2).如果点C在x轴上(不与点A重合),那么当点C的坐标为 时,以B、O、C为顶点的三角形与△AOB相似.
11. 如图,在△ABC中,D是BC的中点,E为△ABC内一点.∠ABE=∠C,∠BAE=∠CAD,连接DE.求证:DE∥AC.
第11题
12. 如图,点P是△ABC的重心,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.求证:a2+b2=5c2.
第12题
6.4 探索三角形相似的条件
第1课时 平行线分线段成比例
及平行线截三角形相似
1. C 2. B 3. 4. 4
5. (1) 连接OD.∵ DE是☉O的切线,∴ OD⊥DE,即∠ODE=90°.∴ ∠ADO+∠BDE=90°.∵ 在△ABC中,∠ACB=90°,∴ ∠A+∠B=90°.∵ OA=OD,∴ ∠A=∠ADO.∴ ∠BDE=∠B.∴ ED=EB.∴ △DBE是等腰三角形 (2) ∵ ∠ACB=90°,AC是☉O的直径,∴ CB是☉O的切线.∵ DE是☉O的切线,∴ ED=EC.∵ ED=EB,∴ EC=EB.∵ OA=OC,∴ OE∥AB.∴ △COE∽△CAB
6. D 7. B 8.
9. 解析:连接OC.根据垂径定理,易得OC⊥BD.由切线的性质,得OC⊥EC.∴ EC∥BD.利用平行线分线段成比例,得==.设EB=x,则AB=3x.∴ OB=OC=AB=x.∴ EO=EB+OB=x.在Rt△OCE中,根据勾股定理,可得EC==2x.∴ ==.
10. (1) △ADE∽△ABC;△EFC∽△ABC;△ADE∽△EFC (2) ∵ DE∥BC,∴ ∠ADE=∠B.∵ ∠ADE=∠EFC,∴ ∠B=∠EFC.∴ AB∥EF,即BD∥EF.∴ 四边形BDEF为平行四边形.∴ DE=BF.∵ DE∥BC,AD∶BD=5∶3,∴ ==.∵ AB∥EF,∴ ==.∵ CF=6,∴ BF=10.∴ DE=10
11. 如图,过点F作FM⊥AB于点M,FN⊥AC于点N,过点D作DT∥AE,交BC于点T.∵ AE平分∠BAC,FM⊥AB,FN⊥AC,∴ FM=FN.∵ BF∶FD=3∶1,∴ S△ABF∶S△ADF=3∶1.∴ AB=3AD.∵ D是AC的中点,∴ AD=CD.∴ AB=AC.∵ DT∥AE,∴ =.∴ ET=CT.∵ DT∥AE,即FE∥DT,∴ BF∶FD=BE∶ET=3∶1.∴ BE=CE.∴ AB+BE=(AC+CE).∵ AB+BE=3,∴ AC+CE=2.∴ △ABC的周长为AB+AC+BC=(AB+BE)+(AC+CE)=3+2=5
第2课时 用两角的关系判定三角形相似
1. B 2. D 3. △MCB 4.
5. ∵ 四边形ABCD是菱形,∴ AB=BC,AC⊥BD.∴ ∠BOC=90°.∵ ∠ABC=60°,∴ △ABC是等边三角形.∴ AB=AC.∵ F为BC的中点,∴ AF⊥BC.∴ ∠BFE=90°.∴ ∠BFE=∠BOC.∵ ∠EBF=∠CBO,∴ △BEF∽△BCO
6. A 7. C
8. 2+2 解析:连接BE交AC于点O,证△ABO∽△ACB,得=,解得AC=2+2或AC=-2+2(不合题意,舍去).
9. 如图所示
10. (1) ∵ =,∴ ∠CAD=∠DAB.∵ DE=AD,∴ ∠DAB=∠E.∴ ∠CAD=∠E.又∵ ∠C=∠C,∴ △CAD∽△CEA (2) 连接BD.∵ AB是☉O的直径,∴ ∠ADB=90°.设∠CAD=∠DAB=α,则∠EAC=2α.由(1),知△CAD∽△CEA,∴ ∠ADC=∠EAC=2α.∵ 四边形ABDC是圆内接四边形,∴ ∠CAB+∠CDB=180°,即2α+2α+90°=180°,解得α=22.5°.∴ ∠ADC=2α=2×22.5°=45°
11. ∵ 四边形ABCD是矩形,∴ CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°.∴ ∠DEP+∠DPE=90°.∵ P为CD的中点,∴ DP=PC=×2=1.由折叠,知EP=AE,∠EPH=∠A=90°,PG=AB=2.∴ ∠DPE+∠CPH=90°.∴ ∠DEP=∠CPH.∴ △EDP∽△PCH.∴ =.设EP=AE=x,则ED=3-x.∵ 在Rt△EDP中,EP2=ED2+DP2,∴ x2=(3-x)2+12,解得x=.∴ EP=AE=,ED=.∴ =.∴ PH=.∴ GH=PG-PH=
第3课时 用两边及夹角的关系判定三角形相似
1. C 2. D 3. (1) 1 (2) 6
4. (1) 连接OD、DB.∵ E是线段OB的中点,DE⊥AB,∴ DE垂直平分OB.∴ DB=OD.∵ 在☉O中,OD=OB,∴ DB=OD=OB.∴ △ODB是等边三角形.∴ ∠BDO=∠DBO=60°.∵ BC=OB=DB,∴ ∠BCD=∠BDC=∠DBO=30°.∴ ∠ODC=∠BDO+∠BDC=90°,即OD⊥CD.∵ OD是☉O的半径,∴ CD是☉O的切线 (2) 连接OP.由题意,得OP=OB=BC=2OE,OC=OB+BC.∴ ==.又∵ ∠POE=∠COP,∴ △OEP∽△OPC.∴ ==
5. B 6. D 7. 8. 1或2
9. (1) 当AC、CD、DB满足CD2=AC·DB时,△ACP∽△PDB 理由:∵ △PCD是等边三角形,∴ ∠PCD=∠PDC=60°,PD=CD=CP.∴ ∠ACP=∠PDB=120°.∴ 当=,即=时,△ACP∽△PDB.∴ 当CD2=AC·DB时,△ACP∽△PDB. (2) ∵ △ACP∽△PDB,∴ ∠A=∠BPD.∵ △PCD是等边三角形,∴ ∠CPD=∠DCP=60°.∴ ∠APB=∠APC+∠CPD+∠BPD=∠APC+∠CPD+∠A=∠DCP+∠CPD=120°
10. 根据题意,得AD=BC=6cm,CD=AB=3cm,∠D=∠MAN=90°.设运动时间为ts,则MA=tcm,NA=(6-2t)cm.分两种情况讨论:① 当△ACD∽△MNA时,=,∴ =,解得t=2.4.② 当△ACD∽△NMA时,=,∴ =,解得t=1.5.综上所述,当运动时间为2.4s或1.5s时,以A、M、N为顶点的三角形与△ACD相似
第4课时 用三边的关系判定三角形相似
1. D 2. B 3. ② 4. (1) 15 (2) 12 8
5. 相似 理由:∵ A'、B'分别是线段OA、OB的中点,∴ A'B'是△AOB的中位线.∴ =.同理,可得=,=.∴ ==.∴ △A'B'C'∽△ABC.
6. B 解析:∵ 长为120cm的木条与三角形木架的最长边相等,∴ 长为120cm的木条不能作为一边.设从长为120 cm的木条上截下的两段分别长为x cm、y cm(x
10. (1) 不相似 理由:∵ CD⊥x轴,∴ ∠ADC=90°.∵ ∠AOB=90°,∴ ∠AOB=∠ADC.∵ A(3,0)、B(0,4)、C(4,2),∴ OA=3,OB=4,OD=4,DC=2.∴ DA=OD-OA=1.∴ ==2,==3.∴ ≠.∴ △AOB与△ADC不相似. (2) 相似 理由:在Rt△AOB中,AB==5,在Rt△ADC中,AC==.过点C作CH⊥OB于点H,则易得四边形ODCH为矩形.∴ CH=OD=4,OH=CD=2.∴ BH=4-2=2.在Rt△BHC中,BC==2.∴ ==,==,==.∴ ==.∴ △ACB∽△ADC.
11. ∵ =,∴ =.∵ ==,∴ ==.∴ △ADC∽△A'D'C'.∴ ∠A=∠A'.∵ =,∴ △ABC∽△A'B'C'
第5课时 与判定三角形相似有关的应用
及三角形的重心
1. D 2. A 3. 4. 1 5. 或
6. (1) 连接BC、OB、OC.∵ AB=AC,∴ 点A在BC的垂直平分线上.∵ OB=OC,∴ 点O在BC的垂直平分线上.∴ AO垂直平分BC.∴ BD=CD (2) ∵ AB2=AO·AD,∴ =.∵ ∠BAO=∠DAB,∴ △ABO∽△ADB.∴ ∠OBA=∠BDA.∵ OB=OA,∴ ∠OBA=∠OAB.∴ ∠OAB=∠BDA.∴ AB=BD.∵ AB=AC,BD=CD,∴ AB=AC=BD=CD.∴ 四边形ABDC是菱形
7. B 8. B
9. 8 解析:延长AC、BD交于点E.在Rt△ADB中,根据勾股定理求出AD=4.先证△BAD≌△EAD,得BD=DE=2.再证△BEC∽△ABD,得=,解得BC=8.
10. (-4,0)或(1,0)或(-1,0)
11. 如图,延长BE,交AC于点F.∵ ∠ABE=∠C,∠BAE=∠CAD,∴ △ABE∽△ACD.∴ =.∵ ∠BAE=∠CAD,∴ ∠BAE+∠DAE=∠CAD+∠DAE,即∠BAD=∠FAE.∵ ∠AEF=∠ABE+∠BAE,∠ADB=∠CAD+∠C,∴ ∠AEF=∠ADB.∴ △EAF∽△DAB.∴ =.∴ =.∵ D是BC的中点,∴ CD=BD.∴ BE=EF.∴ DE是△BCF的中位线.∴ DE∥AC
12. 连接EF,设PF=m,PE=n.∵ 点P是△ABC的重心,∴ E、F分别为AC、BC的中点.∴ EF为△ABC的中位线.∴ EF∥AB,EF=AB,AE=AC,BF=BC.∵ BC=a,AC=b,AB=c,∴ AE=b,BF=a,EF=c.∵ EF∥AB,∴ ∠EFP=∠BAP,∠FEP=∠ABP.∴ △EFP∽△BAP.∴ ===,即==.∴ PB=2n,PA=2m.∵ AF⊥BE,∴ 在Rt△AEP中,由勾股定理,得PE2+PA2=AE2,得n2+4m2=b2①;在Rt△BFP中,由勾股定理,得PF2+PB2=BF2,得m2+4n2=a2②.①+②,得5(n2+m2)=(a2+b2).在Rt△EFP中,由勾股定理,得PE2+PF2=EF2,得n2+m2=c2.∴ 5×c2=(a2+b2),即a2+b2=5c2
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
