6.5 相似三角形的性质(2课时,含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 6.5 相似三角形的性质(2课时,含答案) 2024-2025学年数学苏科版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 176.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 15:21:05 | ||
图片预览


文档简介
6.5 相似三角形的性质
第1课时 相似三角形的周长、面积的性质
1. (2024·内江)已知△ABC与△DEF相似,且相似比为,则△ABC与△DEF的周长之比是 ( )
A. 1∶1 B. 1∶3 C. 1∶6 D. 1∶9
2. 如图,在矩形ABCD中,E是边AD上一点,且AE=2DE,BD与CE相交于点F.若△DEF的面积是3,则△BCF的面积是 ( )
A. 9 B. 12 C. 27 D. 48
3. (2023·泰州)两个相似图形的周长比为3∶2,则它们的面积比为 .
4. 一块3m×2m的矩形广告牌的制作成本是120元,在每平方米制作成本相同的情况下,若将广告牌的四边都扩大为原来的3倍,则扩大后一块矩形广告牌的制作成本是 元.
5. 如图,在△ABC和△DEC中,∠A=∠D,∠BCE=∠ACD.
(1) 求证:△ABC∽△DEC;
(2) 若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.
第5题
6. 两个相似三角形的最短边的长分别为5cm和3cm,他们的周长之差为12cm,那么大三角形的周长为( )
A. 14cm B. 16cm C. 18cm D. 30cm
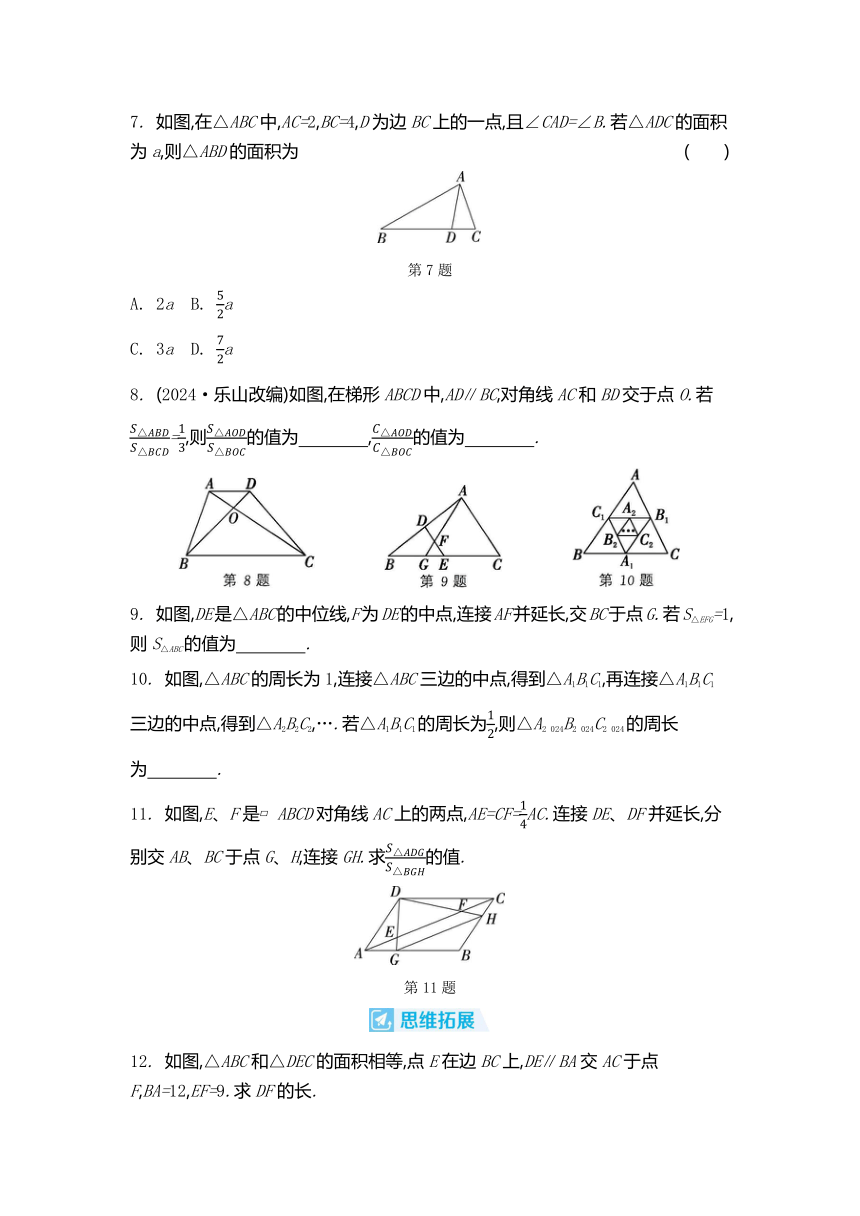
7. 如图,在△ABC中,AC=2,BC=4,D为边BC上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为 ( )
第7题
A. 2a B. a
C. 3a D. a
8. (2024·乐山改编)如图,在梯形ABCD中,AD∥BC,对角线AC和BD交于点O.若=,则的值为 ,的值为 .
9. 如图,DE是△ABC的中位线,F为DE的中点,连接AF并延长,交BC于点G.若S△EFG=1,则S△ABC的值为 .
10. 如图,△ABC的周长为1,连接△ABC三边的中点,得到△A1B1C1,再连接△A1B1C1三边的中点,得到△A2B2C2,….若△A1B1C1的周长为,则△A2 024B2 024C2 024的周长为 .
11. 如图,E、F是 ABCD对角线AC上的两点,AE=CF=AC.连接DE、DF并延长,分别交AB、BC于点G、H,连接GH.求的值.
第11题
12. 如图,△ABC和△DEC的面积相等,点E在边BC上,DE∥BA交AC于点F,BA=12,EF=9.求DF的长.
第12题
第2课时 相似三角形的高、中线、角平分线的性质
1.
用放大镜看一个直角三角形,该三角形的边长放大到原来的10倍后,下列结论错误的是 ( )
A. 斜边上的中线是原来的10倍 B. 斜边上的高是原来的10倍
C. 周长是原来的10倍 D. 最小的内角是原来的10倍
2. 已知△FHB∽△EAD,△FHB和△EAD的周长分别为30和15.若FM和EN分别是上述两个三角形的对应中线,且FM=6,则EN的长为 ( )
A. 3 B. 2 C. 4 D. 5
3. 如图,在△ABC中,EF∥BC,=,作△ABC的角平分线AM,分别交EF、BC于点N、M,则的值为 .
4. 如图,在锐角三角形ABC中,点D、E分别在边AC、AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.若AD=3,AB=5,则的值为 .
5. 如图,正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,试求正方形DEFG的边长.
第5题
第6题
6. 如图,将△ABC沿边BC上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为16,涂色部分三角形的面积为9.若AA'=1,则A'D的长为 ( )
A. 2 B. 3
C. 4 D. 1.5
7. 如图,在矩形ABCD中,AB=6,BC=10,点E、F在边AD上,BF和CE交于点G.若EF=AD,则图中涂色部分的面积为 ( )
A. 25 B. 30 C. 35 D. 40
8. 如图,点G是△ABC的重心,过点G作GD∥BC,交AC于点D,连接AG并延长,交BC于点F,则△AGD与△AFC对应角平分线的比为 .
9. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,D是边AC上的一点,过点D作DF∥AB,交BC于点F,作∠BAC的平分线交DF于点E,连接BE.若△ABE的面积是2,则的值是 .
10. 如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E、F、G、N、M都在△ABC的边上,求△AEM与四边形BCME的面积比.
第10题
11. 求证:相似三角形对应边上的中线之比等于相似比.要求:
(1) 根据如图所示的△ABC及线段A'B'、∠A'(∠A'=∠A),以线段A'B'为一边,在图形上用尺规作出△A'B'C',使得△A'B'C'∽△ABC(不写作法,保留作图痕迹);
(2) 在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
6.5 相似三角形的性质
第1课时 相似三角形的周长、面积的性质
1. B 2. C 3. 9∶4 4. 1080
5. (1) ∵ ∠BCE=∠ACD,∴ ∠BCE+∠ACE=∠ACD+∠ACE.∴ ∠ACB=∠DCE.又∵ ∠A=∠D,∴ △ABC∽△DEC (2) ∵ △ABC∽△DEC,∴ =.∵ S△ABC∶S△DEC=4∶9,∴ =.∵ BC=6,∴ EC=9
6. D 7. C 8.
9. 24 解析:∵ DE是△ABC的中位线,∴ DE∥AC.取AG的中点M,连接DM,证△DFM≌△EFG,得MF=GF=GM=AM,S△DFM=S△EFG=1.∴ S△ADM=2S△DFM=2.证△ADM∽△ABG,得S△ABG=4S△ADM=8.证△EFG∽△CAG,得S△CAG=16S△EFG=16.∴ S△ABC=S△ABG+S△CAG=24.
10.
11. 连接BD.∵ AE=AC,∴ =.∵ 四边形ABCD是平行四边形,∴ BA∥CD,BA=CD,S△ABD=S△BAC =S ABCD.∴ 易得△AEG∽△CED.∴ ==.∴ =.∴ =,S△ADG=S△ABD.同理,可得=.∴ =.∵ ∠GBH=∠ABC,∴ △BGH∽△BAC.∴ =2=.∴ S△BGH=S△BAC=S△ABD.∴ ==×=
12. ∵ DE∥BA,∴ △FEC∽△ABC.∴ ===.∵ △ABC和△DEC的面积相等,∴ =.又∵ △FEC的边EF上的高与△DEC的边DE上的高相同,∴ 结合三角形的面积公式,得=.∵ EF=9,∴ DE=16.∴ DF=DE-EF=16-9=7
第2课时 相似三角形的高、中线、角平分线的性质
1. D 2. A 3. 4.
5. 过点A作AH⊥BC于点H,交GF于点M.∵ △ABC的面积是6,BC=4,∴ ×4AH=6.∴ AH=3.∵ 四边形DEFG是正方形,∴ GF=DG,GF∥DE,即GF∥BC.∴ AH⊥GF.∴ 易得GF=DG=MH.设正方形DEFG的边长为x,则GF=MH=x,AM=3-x.∵ GF∥BC,∴ △AGF∽△ABC.∴ =,即=,解得x=.∴ 正方形DEFG的边长为
6. B 7. C 8. 2∶3 9.
10. 设AD交EM于点P.∵ 四边形EFGH和四边形HGNM均为正方形,∴ EF=EH=HM,EH∥FG,即EM∥BC.∵ AD⊥BC,∴ AP⊥EM.由题意,易得PD=EF.∵ EM∥BC,∴ △AEM∽△ABC.∴ =.∴ =.∴ EF=.∴ EM=5.∵ △AEM∽△ABC,∴ ===.∴ S四边形BCME=S△ABC-S△AEM=3S△AEM.∴ △AEM与四边形BCME的面积比为1∶3
11. (1) 如图,△A'B'C'即为所求 (2) 已知:如图,△A'B'C'∽△ABC,且相似比为k,D是AB的中点,D'是A'B'的中点.求证:=k.证明:∵ D是AB的中点,D'是A'B'的中点,∴ AD=AB,A'D'=A'B'.∴ ==.∵ △A'B'C'∽△ABC,且相似比为k,∴ ==k,∠A'=∠A.∴ =.∴ △A'C'D'∽△ACD.∴ ==k.∴ 相似三角形对应边上的中线之比等于相似比
第1课时 相似三角形的周长、面积的性质
1. (2024·内江)已知△ABC与△DEF相似,且相似比为,则△ABC与△DEF的周长之比是 ( )
A. 1∶1 B. 1∶3 C. 1∶6 D. 1∶9
2. 如图,在矩形ABCD中,E是边AD上一点,且AE=2DE,BD与CE相交于点F.若△DEF的面积是3,则△BCF的面积是 ( )
A. 9 B. 12 C. 27 D. 48
3. (2023·泰州)两个相似图形的周长比为3∶2,则它们的面积比为 .
4. 一块3m×2m的矩形广告牌的制作成本是120元,在每平方米制作成本相同的情况下,若将广告牌的四边都扩大为原来的3倍,则扩大后一块矩形广告牌的制作成本是 元.
5. 如图,在△ABC和△DEC中,∠A=∠D,∠BCE=∠ACD.
(1) 求证:△ABC∽△DEC;
(2) 若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.
第5题
6. 两个相似三角形的最短边的长分别为5cm和3cm,他们的周长之差为12cm,那么大三角形的周长为( )
A. 14cm B. 16cm C. 18cm D. 30cm
7. 如图,在△ABC中,AC=2,BC=4,D为边BC上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为 ( )
第7题
A. 2a B. a
C. 3a D. a
8. (2024·乐山改编)如图,在梯形ABCD中,AD∥BC,对角线AC和BD交于点O.若=,则的值为 ,的值为 .
9. 如图,DE是△ABC的中位线,F为DE的中点,连接AF并延长,交BC于点G.若S△EFG=1,则S△ABC的值为 .
10. 如图,△ABC的周长为1,连接△ABC三边的中点,得到△A1B1C1,再连接△A1B1C1三边的中点,得到△A2B2C2,….若△A1B1C1的周长为,则△A2 024B2 024C2 024的周长为 .
11. 如图,E、F是 ABCD对角线AC上的两点,AE=CF=AC.连接DE、DF并延长,分别交AB、BC于点G、H,连接GH.求的值.
第11题
12. 如图,△ABC和△DEC的面积相等,点E在边BC上,DE∥BA交AC于点F,BA=12,EF=9.求DF的长.
第12题
第2课时 相似三角形的高、中线、角平分线的性质
1.
用放大镜看一个直角三角形,该三角形的边长放大到原来的10倍后,下列结论错误的是 ( )
A. 斜边上的中线是原来的10倍 B. 斜边上的高是原来的10倍
C. 周长是原来的10倍 D. 最小的内角是原来的10倍
2. 已知△FHB∽△EAD,△FHB和△EAD的周长分别为30和15.若FM和EN分别是上述两个三角形的对应中线,且FM=6,则EN的长为 ( )
A. 3 B. 2 C. 4 D. 5
3. 如图,在△ABC中,EF∥BC,=,作△ABC的角平分线AM,分别交EF、BC于点N、M,则的值为 .
4. 如图,在锐角三角形ABC中,点D、E分别在边AC、AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.若AD=3,AB=5,则的值为 .
5. 如图,正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,试求正方形DEFG的边长.
第5题
第6题
6. 如图,将△ABC沿边BC上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为16,涂色部分三角形的面积为9.若AA'=1,则A'D的长为 ( )
A. 2 B. 3
C. 4 D. 1.5
7. 如图,在矩形ABCD中,AB=6,BC=10,点E、F在边AD上,BF和CE交于点G.若EF=AD,则图中涂色部分的面积为 ( )
A. 25 B. 30 C. 35 D. 40
8. 如图,点G是△ABC的重心,过点G作GD∥BC,交AC于点D,连接AG并延长,交BC于点F,则△AGD与△AFC对应角平分线的比为 .
9. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,D是边AC上的一点,过点D作DF∥AB,交BC于点F,作∠BAC的平分线交DF于点E,连接BE.若△ABE的面积是2,则的值是 .
10. 如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E、F、G、N、M都在△ABC的边上,求△AEM与四边形BCME的面积比.
第10题
11. 求证:相似三角形对应边上的中线之比等于相似比.要求:
(1) 根据如图所示的△ABC及线段A'B'、∠A'(∠A'=∠A),以线段A'B'为一边,在图形上用尺规作出△A'B'C',使得△A'B'C'∽△ABC(不写作法,保留作图痕迹);
(2) 在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
6.5 相似三角形的性质
第1课时 相似三角形的周长、面积的性质
1. B 2. C 3. 9∶4 4. 1080
5. (1) ∵ ∠BCE=∠ACD,∴ ∠BCE+∠ACE=∠ACD+∠ACE.∴ ∠ACB=∠DCE.又∵ ∠A=∠D,∴ △ABC∽△DEC (2) ∵ △ABC∽△DEC,∴ =.∵ S△ABC∶S△DEC=4∶9,∴ =.∵ BC=6,∴ EC=9
6. D 7. C 8.
9. 24 解析:∵ DE是△ABC的中位线,∴ DE∥AC.取AG的中点M,连接DM,证△DFM≌△EFG,得MF=GF=GM=AM,S△DFM=S△EFG=1.∴ S△ADM=2S△DFM=2.证△ADM∽△ABG,得S△ABG=4S△ADM=8.证△EFG∽△CAG,得S△CAG=16S△EFG=16.∴ S△ABC=S△ABG+S△CAG=24.
10.
11. 连接BD.∵ AE=AC,∴ =.∵ 四边形ABCD是平行四边形,∴ BA∥CD,BA=CD,S△ABD=S△BAC =S ABCD.∴ 易得△AEG∽△CED.∴ ==.∴ =.∴ =,S△ADG=S△ABD.同理,可得=.∴ =.∵ ∠GBH=∠ABC,∴ △BGH∽△BAC.∴ =2=.∴ S△BGH=S△BAC=S△ABD.∴ ==×=
12. ∵ DE∥BA,∴ △FEC∽△ABC.∴ ===.∵ △ABC和△DEC的面积相等,∴ =.又∵ △FEC的边EF上的高与△DEC的边DE上的高相同,∴ 结合三角形的面积公式,得=.∵ EF=9,∴ DE=16.∴ DF=DE-EF=16-9=7
第2课时 相似三角形的高、中线、角平分线的性质
1. D 2. A 3. 4.
5. 过点A作AH⊥BC于点H,交GF于点M.∵ △ABC的面积是6,BC=4,∴ ×4AH=6.∴ AH=3.∵ 四边形DEFG是正方形,∴ GF=DG,GF∥DE,即GF∥BC.∴ AH⊥GF.∴ 易得GF=DG=MH.设正方形DEFG的边长为x,则GF=MH=x,AM=3-x.∵ GF∥BC,∴ △AGF∽△ABC.∴ =,即=,解得x=.∴ 正方形DEFG的边长为
6. B 7. C 8. 2∶3 9.
10. 设AD交EM于点P.∵ 四边形EFGH和四边形HGNM均为正方形,∴ EF=EH=HM,EH∥FG,即EM∥BC.∵ AD⊥BC,∴ AP⊥EM.由题意,易得PD=EF.∵ EM∥BC,∴ △AEM∽△ABC.∴ =.∴ =.∴ EF=.∴ EM=5.∵ △AEM∽△ABC,∴ ===.∴ S四边形BCME=S△ABC-S△AEM=3S△AEM.∴ △AEM与四边形BCME的面积比为1∶3
11. (1) 如图,△A'B'C'即为所求 (2) 已知:如图,△A'B'C'∽△ABC,且相似比为k,D是AB的中点,D'是A'B'的中点.求证:=k.证明:∵ D是AB的中点,D'是A'B'的中点,∴ AD=AB,A'D'=A'B'.∴ ==.∵ △A'B'C'∽△ABC,且相似比为k,∴ ==k,∠A'=∠A.∴ =.∴ △A'C'D'∽△ACD.∴ ==k.∴ 相似三角形对应边上的中线之比等于相似比
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
