6.6 图形的位似 练习(含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 6.6 图形的位似 练习(含答案) 2024-2025学年数学苏科版九年级下册 | 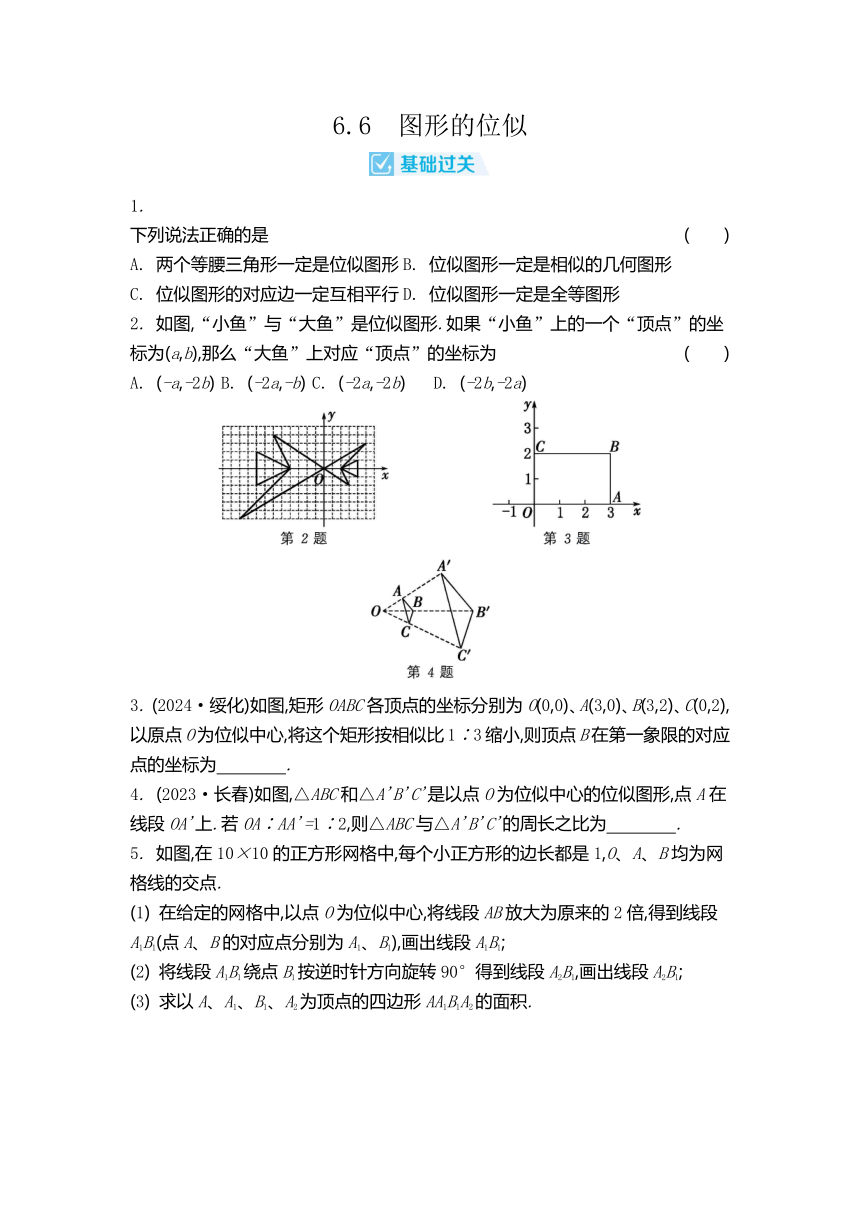 | |
| 格式 | docx | ||
| 文件大小 | 291.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 15:49:13 | ||
图片预览


文档简介
6.6 图形的位似
1.
下列说法正确的是 ( )
A. 两个等腰三角形一定是位似图形 B. 位似图形一定是相似的几何图形
C. 位似图形的对应边一定互相平行 D. 位似图形一定是全等图形
2. 如图,“小鱼”与“大鱼”是位似图形.如果“小鱼”上的一个“顶点”的坐标为(a,b),那么“大鱼”上对应“顶点”的坐标为 ( )
A. (-a,-2b) B. (-2a,-b) C. (-2a,-2b) D. (-2b,-2a)
3. (2024·绥化)如图,矩形OABC各顶点的坐标分别为O(0,0)、A(3,0)、B(3,2)、C(0,2),以原点O为位似中心,将这个矩形按相似比1∶3缩小,则顶点B在第一象限的对应点的坐标为 .
4. (2023·长春)如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,点A在线段OA'上.若OA∶AA'=1∶2,则△ABC与△A'B'C'的周长之比为 .
5. 如图,在10×10的正方形网格中,每个小正方形的边长都是1,O、A、B均为网格线的交点.
(1) 在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A、B的对应点分别为A1、B1),画出线段A1B1;
(2) 将线段A1B1绕点B1按逆时针方向旋转90°得到线段A2B1,画出线段A2B1;
(3) 求以A、A1、B1、A2为顶点的四边形AA1B1A2的面积.
6. 如图,在△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设点B的横坐标是a,则点B的对应点B'的横坐标是 ( )
A. -2a+3 B. -2a+1 C. -2a+2 D. -2a-2
7. (2023·遂宁)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点三角形ABC与格点三角形DEF成位似关系,则位似中心的坐标为 .
8. 在平面直角坐标系中,△AOB的顶点坐标分别为A(2,1)、B(2,0)、O(0,0).若以原点O为位似中心,把△AOB按相似比2∶1放大,则点A的对应点的坐标为 .
9. 如图①,E是线段BC的中点,分别以B、C为直角顶点的△EAB和△EDC均是等腰直角三角形,且在线段BC的同侧.
(1) AE和ED的数量关系为 ,AE和ED的位置关系为 .
(2) 以点E为位似中心,作△EGF与△EAB位似,H是BC所在直线上的一点,连接GH、HD,分别得到图②和图③.
① 在图②中,点F在BE上,△EGF与△EAB的相似比为,H是EC的中点.求证:GH=HD,且GH⊥HD.
② 在图③中,点H在BC的延长线上,△EGF与△EAB的相似比为k.若BC=2,请直接写出当CH的长为多少时,恰好使得GH=HD,且GH⊥HD(用含k的代数式表示).
6.6 图形的位似
1. B 2. C 3. 4. 1∶3
5. (1) 如图,线段A1B1即为所求 (2) 如图,线段A2B1即为所求 (3) 如图,四边形AA1B1A2的面积为6×6-×2×4×4=20
6. A 解析:根据题意,得=.分别过点B、B'作BD⊥x轴、B'E⊥x轴,垂足分别为D、E.∵ 点C的坐标是(1,0),点B的横坐标是a,∴ CD=a-1.证△BDC∽△B'EC,得==.∴ CE=2(a-1).∴ OE=2(a-1)-1=2a-3.∴ 易得点B的对应点B'的横坐标是-2a+3.
7. (-1,0) 8. (4,2)或(-4,-2)
9. (1) AE=ED AE⊥ED (2) ① 根据题意,得∠B=∠C=90°,AB=BE=EC=DC.∵ △EGF与△EAB位似,且相似比为,∴ ∠GFE=∠B=90°,GF=AB,EF=BE.∴ ∠GFE=∠C.∵ H是EC的中点,∴ EH=HC=EC.∴ GF=HC,FH=EF+EH=BE+EC=EC=CD.∴ △HGF≌△DHC.∴ GH=HD,∠GHF=∠HDC.由题意,得∠HDC+∠DHC=90°,∴ ∠GHF+∠DHC=90°.∴ ∠GHD=180°-(∠GHF+∠DHC)=90°,即GH⊥HD.∴ GH=HD,且GH⊥HD ② 当CH的长为k时,恰好使得GH=HD,且GH⊥HD
1.
下列说法正确的是 ( )
A. 两个等腰三角形一定是位似图形 B. 位似图形一定是相似的几何图形
C. 位似图形的对应边一定互相平行 D. 位似图形一定是全等图形
2. 如图,“小鱼”与“大鱼”是位似图形.如果“小鱼”上的一个“顶点”的坐标为(a,b),那么“大鱼”上对应“顶点”的坐标为 ( )
A. (-a,-2b) B. (-2a,-b) C. (-2a,-2b) D. (-2b,-2a)
3. (2024·绥化)如图,矩形OABC各顶点的坐标分别为O(0,0)、A(3,0)、B(3,2)、C(0,2),以原点O为位似中心,将这个矩形按相似比1∶3缩小,则顶点B在第一象限的对应点的坐标为 .
4. (2023·长春)如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,点A在线段OA'上.若OA∶AA'=1∶2,则△ABC与△A'B'C'的周长之比为 .
5. 如图,在10×10的正方形网格中,每个小正方形的边长都是1,O、A、B均为网格线的交点.
(1) 在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A、B的对应点分别为A1、B1),画出线段A1B1;
(2) 将线段A1B1绕点B1按逆时针方向旋转90°得到线段A2B1,画出线段A2B1;
(3) 求以A、A1、B1、A2为顶点的四边形AA1B1A2的面积.
6. 如图,在△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设点B的横坐标是a,则点B的对应点B'的横坐标是 ( )
A. -2a+3 B. -2a+1 C. -2a+2 D. -2a-2
7. (2023·遂宁)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点三角形ABC与格点三角形DEF成位似关系,则位似中心的坐标为 .
8. 在平面直角坐标系中,△AOB的顶点坐标分别为A(2,1)、B(2,0)、O(0,0).若以原点O为位似中心,把△AOB按相似比2∶1放大,则点A的对应点的坐标为 .
9. 如图①,E是线段BC的中点,分别以B、C为直角顶点的△EAB和△EDC均是等腰直角三角形,且在线段BC的同侧.
(1) AE和ED的数量关系为 ,AE和ED的位置关系为 .
(2) 以点E为位似中心,作△EGF与△EAB位似,H是BC所在直线上的一点,连接GH、HD,分别得到图②和图③.
① 在图②中,点F在BE上,△EGF与△EAB的相似比为,H是EC的中点.求证:GH=HD,且GH⊥HD.
② 在图③中,点H在BC的延长线上,△EGF与△EAB的相似比为k.若BC=2,请直接写出当CH的长为多少时,恰好使得GH=HD,且GH⊥HD(用含k的代数式表示).
6.6 图形的位似
1. B 2. C 3. 4. 1∶3
5. (1) 如图,线段A1B1即为所求 (2) 如图,线段A2B1即为所求 (3) 如图,四边形AA1B1A2的面积为6×6-×2×4×4=20
6. A 解析:根据题意,得=.分别过点B、B'作BD⊥x轴、B'E⊥x轴,垂足分别为D、E.∵ 点C的坐标是(1,0),点B的横坐标是a,∴ CD=a-1.证△BDC∽△B'EC,得==.∴ CE=2(a-1).∴ OE=2(a-1)-1=2a-3.∴ 易得点B的对应点B'的横坐标是-2a+3.
7. (-1,0) 8. (4,2)或(-4,-2)
9. (1) AE=ED AE⊥ED (2) ① 根据题意,得∠B=∠C=90°,AB=BE=EC=DC.∵ △EGF与△EAB位似,且相似比为,∴ ∠GFE=∠B=90°,GF=AB,EF=BE.∴ ∠GFE=∠C.∵ H是EC的中点,∴ EH=HC=EC.∴ GF=HC,FH=EF+EH=BE+EC=EC=CD.∴ △HGF≌△DHC.∴ GH=HD,∠GHF=∠HDC.由题意,得∠HDC+∠DHC=90°,∴ ∠GHF+∠DHC=90°.∴ ∠GHD=180°-(∠GHF+∠DHC)=90°,即GH⊥HD.∴ GH=HD,且GH⊥HD ② 当CH的长为k时,恰好使得GH=HD,且GH⊥HD
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
