6.7 用相似三角形解决问题 练习(2课时、含答案)2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 6.7 用相似三角形解决问题 练习(2课时、含答案)2024-2025学年数学苏科版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 213.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览


文档简介
6.7 用相似三角形解决问题
第1课时 用平行投影解决问题
1.
下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的是 ( )
2. 小刚身高1.7m,测得他站立在阳光下的影长为0.85m,紧接着他把手臂竖直举起,测得影长为1.1m,那么小刚举起的手臂超出头顶 ( )
A. 0.5m B. 0.55m C. 0.6m D. 2.2m
3. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2m,它的影长FD是4m,同一时刻测得OA是268m,则金字塔的高度BO是 m.
4. 如图,将旗帜降到离地面2m(即AH=2m)时,发现旗帜在太阳光下的影子顶端C到旗杆底部H的距离为3m,同时测得旗杆顶端落在地面的影子D到旗杆底部H的距离为21m,则旗杆的高为 m.
5. (2024·自贡)如图,在江姐故里广场上的点E处,同学们先找到与雕塑底部B处于同一水平线的D、G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到点D'处.采用同样方法,测得C'G'=1.2m,D'G'=2m.求雕塑的高度AB(精确到1m).
第5题
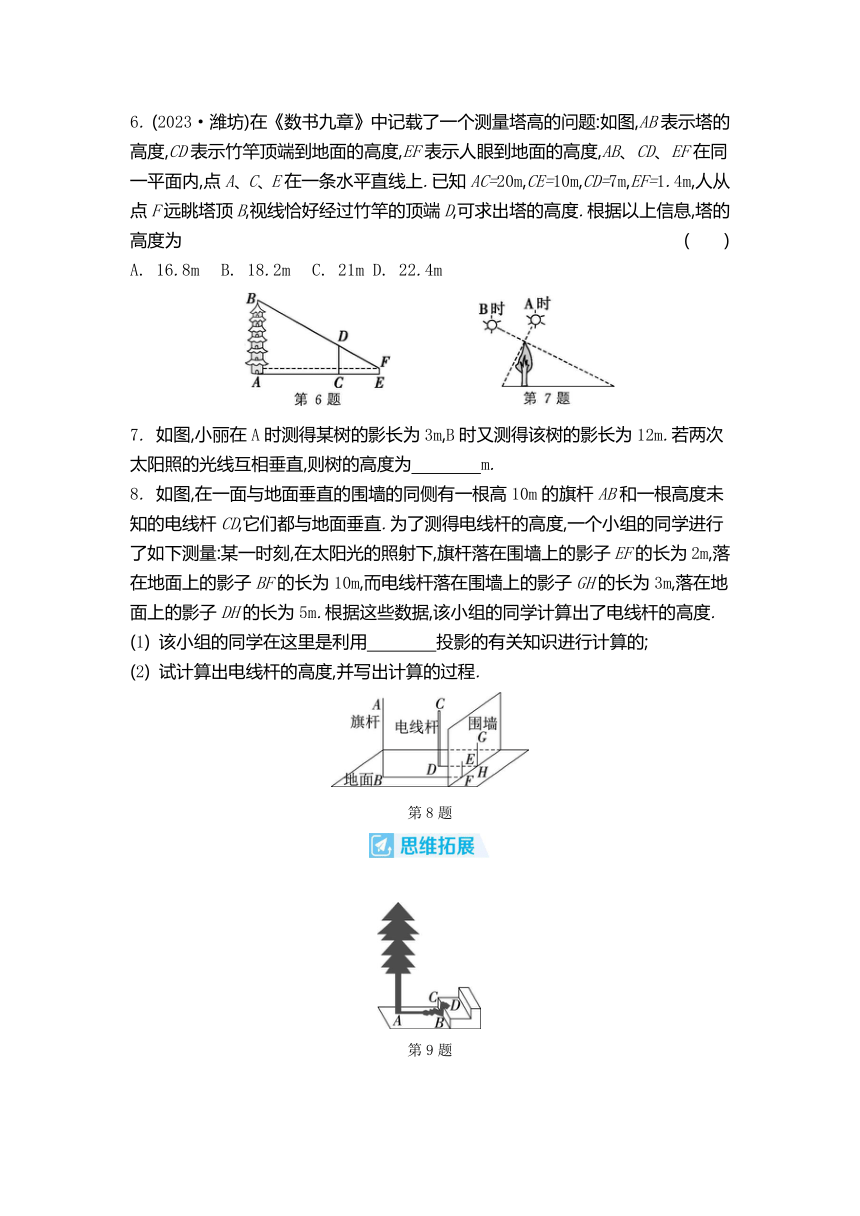
6. (2023·潍坊)在《数书九章》中记载了一个测量塔高的问题:如图,AB表示塔的高度,CD表示竹竿顶端到地面的高度,EF表示人眼到地面的高度,AB、CD、EF在同一平面内,点A、C、E在一条水平直线上.已知AC=20m,CE=10m,CD=7m,EF=1.4m,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,可求出塔的高度.根据以上信息,塔的高度为 ( )
A. 16.8m B. 18.2m C. 21m D. 22.4m
7. 如图,小丽在A时测得某树的影长为3m,B时又测得该树的影长为12m.若两次太阳照的光线互相垂直,则树的高度为 m.
8. 如图,在一面与地面垂直的围墙的同侧有一根高10m的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直.为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光的照射下,旗杆落在围墙上的影子EF的长为2m,落在地面上的影子BF的长为10m,而电线杆落在围墙上的影子GH的长为3m,落在地面上的影子DH的长为5m.根据这些数据,该小组的同学计算出了电线杆的高度.
(1) 该小组的同学在这里是利用 投影的有关知识进行计算的;
(2) 试计算出电线杆的高度,并写出计算的过程.
第8题
第9题
9. 某兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长1m的竹竿的影长为0.4m,同时另一名同学在测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影长CD为0.2m,一级台阶的高为0.3m(如图).若此时落在地面上的影长AB为4.4m,则这棵树的高度为
( )
A. 11.5m B. 11.75m
C. 11.8m D. 12.25m
第2课时 用中心投影解决问题
1. 如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是 ( )
2. (2024·镇江)如图,小杰从灯杆AB的底部点B处沿水平直线前进到达点C处,他在灯光下的影长CD=3m,然后他转身按原路返回到点B处,返回过程中小杰在灯光下的影长可以是( )
A. 4.5m B. 4m C. 3.5m D. 2.5m
3. (2024·凉山)如图,一块面积为60cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1.若OB∶BB1=2∶3,则△A1B1C1的面积是 cm2.
4. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m、1.5m,且小军、小珠的身高分别为1.8m、1.5m.求路灯的高.
第4题
5. 圆桌面(圆桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的圆桌面后,在地面上形成如图所示的圆环(涂色部分).已知圆桌面的直径为1.2m,圆桌面离地面1m,灯泡离地面3m,则在地面上形成的圆环(涂色部分)的面积是 ( )
第5题
A. 0.324πm2
B. 0.288πm2
C. 1.08πm2
D. 0.72πm2
6. 如图,小丁同学在晚上从路灯AC走向路灯BD,当他走到点P处时,发现身后他影子的顶部刚好接触到路灯AC的底部A;当他向前再步行20m到达点Q处时,发现身前他影子的顶部刚好接触到路灯BD的底部B.若小丁同学的身高是1.5m,两盏路灯的高度都是9m,则两盏路灯之间的距离是 ( )
A. 24m B. 25m C. 28m D. 30m
7. 如图,路灯距地面8m(即OP=8m),身高1.6m的小明从距路灯底部(点O)20m远的点A出发,沿OA所在的直线行走14m到达点B时,小明影子的长度变 (填“长”或“短”)了 m.
8. 小明利用灯光下自己的影长来测量路灯的高度.如图,CD和EF是两盏等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(点D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1) 小明距离路灯CD多远
(2) 求路灯的高度.
第8题
9. 晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高 ”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿着直线NQ移动,如图,当小聪站在广场的点A处(距点N 5块地砖长)时,其影长AD恰好为1块地砖长;当小军站在点B处(距点N 9块地砖长)时,其影长BF恰好为2块地砖长.广场地面由边长为0.8m的正方形地砖铺成,小聪的身高AC为1.6m,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军的身高BE(精确到0.01m).
第9题
6.7 用相似三角形解决问题
第1课时 用平行投影解决问题
1. C 2. A 3. 134 4. 14
5. 根据题意,得∠CDG=∠ADB,∠CGD=∠ABD=90°,∴ △DCG∽△DAB.∴ =.设AB=xm,BD=ym,则=,∴ y=x.同理,可得=.∴ =.∴ =,解得x=28.8.经检验,x=28.8是上述方程的解,且符合题意.∴ AB≈29m.∴ 雕塑的高度AB约为29m
6. B 7. 6
8. (1) 平行 (2) 过点E作EM⊥AB于点M,过点G作GN⊥CD于点N,则易得MB=EF=2m,ND=GH=3m,ME=BF=10m,NG=DH=5m.∴ AM=AB-MB=8m.由平行投影的性质,得=.设CD=xm,即=,解得x=7,即电线杆的高度为7m
9. C 解析:设产生水平影长之和的树的高度为xm.根据平行投影的性质,得=,解得x=11.5.∴ 这棵树的高度为11.5+0.3=11.8(m).
第2课时 用中心投影解决问题
1. D 2. D 3. 375
4. 如图(根据题意画示意图,并标注字母),根据题意,知CD∥AB∥MN.∴ △CDE∽△ABE,△MNF∽△ABF.∴ =,=.设AB=xm,BD=ym.∵ CD=1.8m,DE=1.8m,MN=1.5m,FN=1.5m,DN=2.7m,∴ ∴ 经检验,是原分式方程组的解,且符合题意.∴ 路灯的高为3m
5. D 6. D 7. 短 3.5
8. (1) 设DB=xm.根据题意,得AB∥CD.∴ △QAB∽△QCD.∴ =.同理,可得=.∵ CD=EF,∴ =,即=,解得x=12.经检验,x=12是原分式方程的解,且符合题意.∴ 小明距离路灯CD12m远 (2) 由(1),得=.设CD=ym,∴ =.∴ y=6.经检验,y=6是原分式方程的解,且符合题意.∴ 路灯的高度为6m
9. 根据题意,易得AN=4m,AD=0.8m,BN=7.2m,BF=1.6m.∵ MN⊥NQ,AC⊥NQ,∴ MN∥AC.∴ △CAD∽△MND.∴ =.∴ MN===9.6(m).同理,可得△EBF∽△MNF.∴ =.∴ EB==≈1.75(m).∴ 小军的身高BE约为1.75m
第1课时 用平行投影解决问题
1.
下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的是 ( )
2. 小刚身高1.7m,测得他站立在阳光下的影长为0.85m,紧接着他把手臂竖直举起,测得影长为1.1m,那么小刚举起的手臂超出头顶 ( )
A. 0.5m B. 0.55m C. 0.6m D. 2.2m
3. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2m,它的影长FD是4m,同一时刻测得OA是268m,则金字塔的高度BO是 m.
4. 如图,将旗帜降到离地面2m(即AH=2m)时,发现旗帜在太阳光下的影子顶端C到旗杆底部H的距离为3m,同时测得旗杆顶端落在地面的影子D到旗杆底部H的距离为21m,则旗杆的高为 m.
5. (2024·自贡)如图,在江姐故里广场上的点E处,同学们先找到与雕塑底部B处于同一水平线的D、G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到点D'处.采用同样方法,测得C'G'=1.2m,D'G'=2m.求雕塑的高度AB(精确到1m).
第5题
6. (2023·潍坊)在《数书九章》中记载了一个测量塔高的问题:如图,AB表示塔的高度,CD表示竹竿顶端到地面的高度,EF表示人眼到地面的高度,AB、CD、EF在同一平面内,点A、C、E在一条水平直线上.已知AC=20m,CE=10m,CD=7m,EF=1.4m,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,可求出塔的高度.根据以上信息,塔的高度为 ( )
A. 16.8m B. 18.2m C. 21m D. 22.4m
7. 如图,小丽在A时测得某树的影长为3m,B时又测得该树的影长为12m.若两次太阳照的光线互相垂直,则树的高度为 m.
8. 如图,在一面与地面垂直的围墙的同侧有一根高10m的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直.为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光的照射下,旗杆落在围墙上的影子EF的长为2m,落在地面上的影子BF的长为10m,而电线杆落在围墙上的影子GH的长为3m,落在地面上的影子DH的长为5m.根据这些数据,该小组的同学计算出了电线杆的高度.
(1) 该小组的同学在这里是利用 投影的有关知识进行计算的;
(2) 试计算出电线杆的高度,并写出计算的过程.
第8题
第9题
9. 某兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长1m的竹竿的影长为0.4m,同时另一名同学在测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影长CD为0.2m,一级台阶的高为0.3m(如图).若此时落在地面上的影长AB为4.4m,则这棵树的高度为
( )
A. 11.5m B. 11.75m
C. 11.8m D. 12.25m
第2课时 用中心投影解决问题
1. 如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是 ( )
2. (2024·镇江)如图,小杰从灯杆AB的底部点B处沿水平直线前进到达点C处,他在灯光下的影长CD=3m,然后他转身按原路返回到点B处,返回过程中小杰在灯光下的影长可以是( )
A. 4.5m B. 4m C. 3.5m D. 2.5m
3. (2024·凉山)如图,一块面积为60cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1.若OB∶BB1=2∶3,则△A1B1C1的面积是 cm2.
4. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m、1.5m,且小军、小珠的身高分别为1.8m、1.5m.求路灯的高.
第4题
5. 圆桌面(圆桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的圆桌面后,在地面上形成如图所示的圆环(涂色部分).已知圆桌面的直径为1.2m,圆桌面离地面1m,灯泡离地面3m,则在地面上形成的圆环(涂色部分)的面积是 ( )
第5题
A. 0.324πm2
B. 0.288πm2
C. 1.08πm2
D. 0.72πm2
6. 如图,小丁同学在晚上从路灯AC走向路灯BD,当他走到点P处时,发现身后他影子的顶部刚好接触到路灯AC的底部A;当他向前再步行20m到达点Q处时,发现身前他影子的顶部刚好接触到路灯BD的底部B.若小丁同学的身高是1.5m,两盏路灯的高度都是9m,则两盏路灯之间的距离是 ( )
A. 24m B. 25m C. 28m D. 30m
7. 如图,路灯距地面8m(即OP=8m),身高1.6m的小明从距路灯底部(点O)20m远的点A出发,沿OA所在的直线行走14m到达点B时,小明影子的长度变 (填“长”或“短”)了 m.
8. 小明利用灯光下自己的影长来测量路灯的高度.如图,CD和EF是两盏等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(点D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1) 小明距离路灯CD多远
(2) 求路灯的高度.
第8题
9. 晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高 ”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿着直线NQ移动,如图,当小聪站在广场的点A处(距点N 5块地砖长)时,其影长AD恰好为1块地砖长;当小军站在点B处(距点N 9块地砖长)时,其影长BF恰好为2块地砖长.广场地面由边长为0.8m的正方形地砖铺成,小聪的身高AC为1.6m,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军的身高BE(精确到0.01m).
第9题
6.7 用相似三角形解决问题
第1课时 用平行投影解决问题
1. C 2. A 3. 134 4. 14
5. 根据题意,得∠CDG=∠ADB,∠CGD=∠ABD=90°,∴ △DCG∽△DAB.∴ =.设AB=xm,BD=ym,则=,∴ y=x.同理,可得=.∴ =.∴ =,解得x=28.8.经检验,x=28.8是上述方程的解,且符合题意.∴ AB≈29m.∴ 雕塑的高度AB约为29m
6. B 7. 6
8. (1) 平行 (2) 过点E作EM⊥AB于点M,过点G作GN⊥CD于点N,则易得MB=EF=2m,ND=GH=3m,ME=BF=10m,NG=DH=5m.∴ AM=AB-MB=8m.由平行投影的性质,得=.设CD=xm,即=,解得x=7,即电线杆的高度为7m
9. C 解析:设产生水平影长之和的树的高度为xm.根据平行投影的性质,得=,解得x=11.5.∴ 这棵树的高度为11.5+0.3=11.8(m).
第2课时 用中心投影解决问题
1. D 2. D 3. 375
4. 如图(根据题意画示意图,并标注字母),根据题意,知CD∥AB∥MN.∴ △CDE∽△ABE,△MNF∽△ABF.∴ =,=.设AB=xm,BD=ym.∵ CD=1.8m,DE=1.8m,MN=1.5m,FN=1.5m,DN=2.7m,∴ ∴ 经检验,是原分式方程组的解,且符合题意.∴ 路灯的高为3m
5. D 6. D 7. 短 3.5
8. (1) 设DB=xm.根据题意,得AB∥CD.∴ △QAB∽△QCD.∴ =.同理,可得=.∵ CD=EF,∴ =,即=,解得x=12.经检验,x=12是原分式方程的解,且符合题意.∴ 小明距离路灯CD12m远 (2) 由(1),得=.设CD=ym,∴ =.∴ y=6.经检验,y=6是原分式方程的解,且符合题意.∴ 路灯的高度为6m
9. 根据题意,易得AN=4m,AD=0.8m,BN=7.2m,BF=1.6m.∵ MN⊥NQ,AC⊥NQ,∴ MN∥AC.∴ △CAD∽△MND.∴ =.∴ MN===9.6(m).同理,可得△EBF∽△MNF.∴ =.∴ EB==≈1.75(m).∴ 小军的身高BE约为1.75m
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
