7.2 正弦、余弦 练习(2课时、含答案)2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 7.2 正弦、余弦 练习(2课时、含答案)2024-2025学年数学苏科版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 173.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览



文档简介
7.2 正弦、余弦
第1课时 正弦、余弦的概念
1.
如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是 ( )
A. B. C. D.
2. 如图,一辆小车沿倾斜角为α的斜坡向上行驶13m.若cosα=,则小车上升的高度是 ( )
A. 5m B. 6m C. 6.5m D. 12m
3. 在Rt△ABC中,∠C=90°,AC=1,BC=,则cosA的值为 .
4. 用计算器计算:sin35°≈ ,cos35°44'27″≈ (精确到0.01).
5. 如图,关于α与β的同一种三角函数值,有下列三个结论:① tanα>tanβ;② sinα>sinβ;③ cosα>cosβ.其中,正确的是 (填序号).
6. 如图,在正方形ABCD中,M是AD的中点,BE=3AE.求∠ECM的正切值、正弦值及余弦值.
第6题
7. 如图,在由边长为1的小正方形构成的网格中,点A、B、C都在格点上,以AB为直径的圆经过点C、D,则cos∠ADC的值为 ( )
第7题
A. B.
C. D.
8. 在Rt△ABC中,∠C=90°,sinA=,则tanB的值为 ( )
A. B. C. D.
9. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若CD=12,BD=5,则tanA的值为 ,cos∠ACD的值为 .
10. 已知等腰三角形的底边和底边上的高分别是方程x2-10x+24=0的两个根,则该等腰三角形底角的正弦值是 .
11. (2024·浙江)如图,在△ABC中,AD⊥BC,AE是边BC上的中线,AB=10,AD=6,tan∠ACB=1.求:
(1) BC的长;
(2) sin∠DAE的值.
第11题
12. (2023·扬州改编)如图,在△ABC中,∠ACB=90°,D是AB上一点,且∠BCD=∠A,点O在BC上,以点O为圆心的圆经过C、D两点.
(1) 试判断直线AB与☉O的位置关系,并说明理由;
(2) 若cosB=,☉O的半径为3,求AC的长.
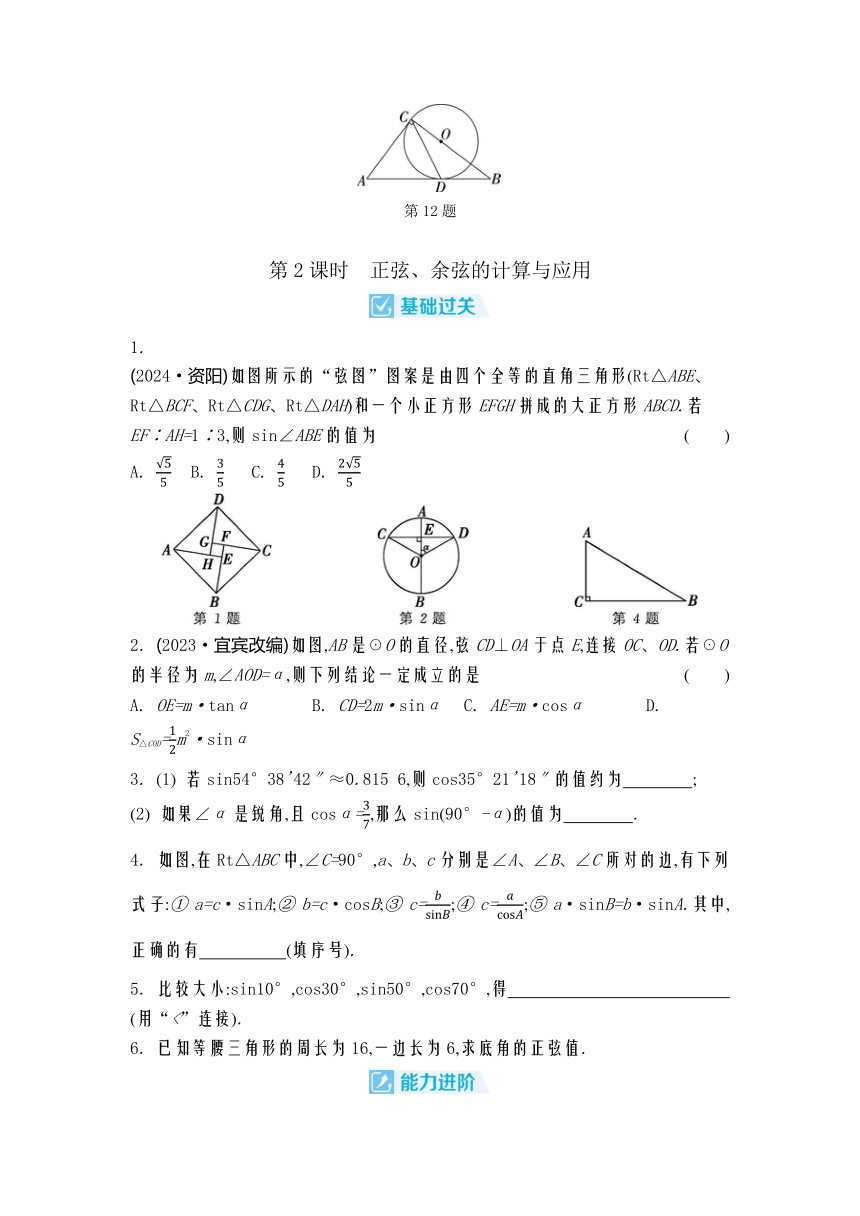
第12题
第2课时 正弦、余弦的计算与应用
1.
(2024·资阳)如图所示的“弦图”图案是由四个全等的直角三角形(Rt△ABE、Rt△BCF、Rt△CDG、Rt△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF∶AH=1∶3,则sin∠ABE的值为 ( )
A. B. C. D.
2. (2023·宜宾改编)如图,AB是☉O的直径,弦CD⊥OA于点E,连接OC、OD.若☉O的半径为m,∠AOD=α,则下列结论一定成立的是 ( )
A. OE=m·tanα B. CD=2m·sinα C. AE=m·cosα D. S△COD=m2·sinα
3. (1) 若sin54°38'42″≈0.815 6,则cos35°21'18″的值约为 ;
(2) 如果∠α是锐角,且cosα=,那么sin(90°-α)的值为 .
4. 如图,在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C所对的边,有下列式子:① a=c·sinA;② b=c·cosB;③ c=;④ c=;⑤ a·sinB=b·sinA.其中,正确的有 (填序号).
5. 比较大小:sin10°,cos30°,sin50°,cos70°,得 (用“<”连接).
6. 已知等腰三角形的周长为16,一边长为6,求底角的正弦值.
7. (2024·包头)如图,在矩形ABCD中,E、F是边BC上两点,且BE=EF=FC,连接DE、AF,DE与AF相交于点G,连接BG.若AB=4,BC=6,则sin∠GBF的值为 ( )
第7题
A. B.
C. D.
8. 如图,在6×6的正方形网格中,△ABC的顶点A、B、C都在网格线上,且都是小正方形边的中点,则sinA的值为 .
9. 如图,在△ABC中,∠ACB=90°,D为边AB的中点,连接CD.若BC=4,CD=3,则cos ∠DCB的值为 .
10. 如图,在Rt△ABC中,∠BAC=90°,斜边BC上的高AD=8,sin B=,则AC的长为 .
11. (2024·上海)在 ABCD中,∠ABC是锐角,将CD沿直线l翻折至AB所在直线,点C、D的对应点分别为C'、D'.若AC'∶AB∶BC=1∶3∶7,则cos∠ABC的值为 .
12. (2023·深圳)如图,在菱形ABCD中,cosA=,过点C作CE⊥AB,交AB的延长线于点E,过点E作EF⊥AD,交AD于点F.若S菱形ABCD=24,求EF·BC的值.
第12题
13. (2024·遂宁)小明的书桌上有一个L型台灯,灯柱AB高40cm,他发现当灯带BC与水平线BM的夹角为9°时(如图①),灯带的直射宽度DE(BD⊥BC,CE⊥BC)为35cm,但此时灯的直射宽度不够,当他把灯带调整到与水平线夹角为30°时(如图②),直射宽度刚好合适,求此时台灯最高点C到桌面的距离(精确到0.1cm,参考数据:sin9°≈0.16,cos9°≈0.99,sin30°=0.5,cos30°≈0.87).
7.2 正弦、余弦
第1课时 正弦、余弦的概念
1. D 2. A 3. 4. 0.57 0.81 5. ①②
6. 设正方形ABCD的边长为4a.∵ BE=3AE,∴ AE=a,BE=3a.∵ 四边形ABCD是正方形,∴ ∠A=∠B=∠D=90°.在Rt△BCE中,BE=3a,BC=4a,∴ 由勾股定理,得EC==5a.∵ M是AD的中点,∴ AM=MD=AD=2a.∴ 在Rt△AEM中,由勾股定理,得EM==a,在Rt△CDM中,由勾股定理,得MC==2a.∴ EM2+MC2=EC2.∴ ∠EMC=90°.∴ 在Rt△CEM中,tan∠ECM==,sin∠ECM==,cos∠ECM==
7. B 8. C 9. 10. 或
11. (1) ∵ AD⊥BC,AB=10,AD=6,∴ 由勾股定理,得BD===8.∵ 在Rt△ADC中,tan∠ACB=,tan∠ACB=1,∴ CD=AD=6.∴ BC=BD+CD=8+6=14 (2) ∵ AE是边BC上的中线,∴ CE=BC=7.∴ DE=CE-CD=7-6=1.∵ AD⊥BC,∴ 由勾股定理,得AE===.∴ 在Rt△ADE中,sin∠DAE===
12. (1) 直线AB与☉O相切 理由:连接OD.∵ OC=OD,∴ ∠OCD=∠ODC.∴ ∠BOD=∠OCD+∠ODC=2∠BCD.∴ ∠BCD=∠BOD.∵ ∠BCD=∠A,∴ ∠BOD=∠A.∵ 在△ABC中,∠ACB=90°,∴ ∠A+∠B=90°.∴ ∠BOD+∠B=90°.∴ 在△ODB中,∠BDO=90°.∴ OD⊥AB.∵ OD是☉O的半径,∴ 直线AB与☉O相切. (2) ∵ 在Rt△ODB中,cosB==,∴ 设BD=4x(x>0),则OB=5x.∴ 由勾股定理,得OD==3x.∵ OD=OC=3,∴ 3x=3,解得x=1.∴ OB=5x=5.∴ BC=OB+OC=8. ∵ 在Rt△ACB中,cosB==,∴ AB=10.∴ 由勾股定理,得AC==6
第2课时 正弦、余弦的计算与应用
1. C 2. B 3. (1) 0.8156 (2) 4. ①③⑤ 5. sin10°6. 设这个等腰三角形为△ABC,且AB=AC.分两种情况讨论:① 当AB=AC=6时,BC=16-6×2=4.过点A作AD⊥BC于点D.∴ BD=BC=2,∠ADB=90°.∴ 在Rt△ABD中,由勾股定理,得AD==4.∴ sinB===.② 当BC=6时,AB=AC=×(16-6)=5.过点A作AD⊥BC于点D.∴ BD=BC=3,∠ADB=90°.∴ 在Rt△ABD中,由勾股定理,得AD==4.∴ sinB==.综上所述,底角的正弦值为或
7. A 8. 9.
10. 10 解析:先利用同角的余角相等说明∠B=∠DAC,即sin B=sin ∠DAC,即=,由此可设DC=3k(k>0),则AC=5k,在Rt△ADC中,根据勾股定理,得AD=4k.∵ AD=8,∴ 4k=8,解得k=2.∴ AC=5×2=10.
11. 或 解析:分点C'在线段AB上和点C'在BA的延长线上两种情况讨论.
12. ∵ 四边形ABCD是菱形,∴ AD∥BC,AB=BC.∴ ∠CBE=∠A.∵ cosA=,∴ cos∠CBE=.∵ CE⊥AB,∴ ∠CEB=90°.∴ 在Rt△CEB中,cos∠CBE==.∴ BE=BC.∴ AE=AB+BE=AB+BC=AB+AB=AB.∵ EF⊥AD,CE⊥AB,∴ ∠AFE=∠BEC=90°.∴ △AFE∽△BEC.∴ =.∴ EF·BC=AE·CE=AB·CE=S菱形ABCD=×24=32
13. 在题图①中,∵ DB⊥BC,EC⊥BC,∴ BD∥EC.∵ BM∥DE,∴ 四边形BDEM是平行四边形.∴ BM=DE=35cm.∵ CE⊥BC,∴ 在Rt△BCM中,BC=BM·cos9°≈35×0.99=34.65(cm).如图,过点C作CK⊥AE'于点K,交BM于点J,则四边形BAKJ为矩形.∴ BA=JK=40cm,∠BJK=∠BJC=90°.∴ 在Rt△BJC中,CJ=BC·sin30°=17.325cm.∴ CK=CJ+JK=17.325+40≈57.3(cm).∴ 台灯最高点C到桌面的距离约为57.3cm
第1课时 正弦、余弦的概念
1.
如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是 ( )
A. B. C. D.
2. 如图,一辆小车沿倾斜角为α的斜坡向上行驶13m.若cosα=,则小车上升的高度是 ( )
A. 5m B. 6m C. 6.5m D. 12m
3. 在Rt△ABC中,∠C=90°,AC=1,BC=,则cosA的值为 .
4. 用计算器计算:sin35°≈ ,cos35°44'27″≈ (精确到0.01).
5. 如图,关于α与β的同一种三角函数值,有下列三个结论:① tanα>tanβ;② sinα>sinβ;③ cosα>cosβ.其中,正确的是 (填序号).
6. 如图,在正方形ABCD中,M是AD的中点,BE=3AE.求∠ECM的正切值、正弦值及余弦值.
第6题
7. 如图,在由边长为1的小正方形构成的网格中,点A、B、C都在格点上,以AB为直径的圆经过点C、D,则cos∠ADC的值为 ( )
第7题
A. B.
C. D.
8. 在Rt△ABC中,∠C=90°,sinA=,则tanB的值为 ( )
A. B. C. D.
9. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若CD=12,BD=5,则tanA的值为 ,cos∠ACD的值为 .
10. 已知等腰三角形的底边和底边上的高分别是方程x2-10x+24=0的两个根,则该等腰三角形底角的正弦值是 .
11. (2024·浙江)如图,在△ABC中,AD⊥BC,AE是边BC上的中线,AB=10,AD=6,tan∠ACB=1.求:
(1) BC的长;
(2) sin∠DAE的值.
第11题
12. (2023·扬州改编)如图,在△ABC中,∠ACB=90°,D是AB上一点,且∠BCD=∠A,点O在BC上,以点O为圆心的圆经过C、D两点.
(1) 试判断直线AB与☉O的位置关系,并说明理由;
(2) 若cosB=,☉O的半径为3,求AC的长.
第12题
第2课时 正弦、余弦的计算与应用
1.
(2024·资阳)如图所示的“弦图”图案是由四个全等的直角三角形(Rt△ABE、Rt△BCF、Rt△CDG、Rt△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF∶AH=1∶3,则sin∠ABE的值为 ( )
A. B. C. D.
2. (2023·宜宾改编)如图,AB是☉O的直径,弦CD⊥OA于点E,连接OC、OD.若☉O的半径为m,∠AOD=α,则下列结论一定成立的是 ( )
A. OE=m·tanα B. CD=2m·sinα C. AE=m·cosα D. S△COD=m2·sinα
3. (1) 若sin54°38'42″≈0.815 6,则cos35°21'18″的值约为 ;
(2) 如果∠α是锐角,且cosα=,那么sin(90°-α)的值为 .
4. 如图,在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C所对的边,有下列式子:① a=c·sinA;② b=c·cosB;③ c=;④ c=;⑤ a·sinB=b·sinA.其中,正确的有 (填序号).
5. 比较大小:sin10°,cos30°,sin50°,cos70°,得 (用“<”连接).
6. 已知等腰三角形的周长为16,一边长为6,求底角的正弦值.
7. (2024·包头)如图,在矩形ABCD中,E、F是边BC上两点,且BE=EF=FC,连接DE、AF,DE与AF相交于点G,连接BG.若AB=4,BC=6,则sin∠GBF的值为 ( )
第7题
A. B.
C. D.
8. 如图,在6×6的正方形网格中,△ABC的顶点A、B、C都在网格线上,且都是小正方形边的中点,则sinA的值为 .
9. 如图,在△ABC中,∠ACB=90°,D为边AB的中点,连接CD.若BC=4,CD=3,则cos ∠DCB的值为 .
10. 如图,在Rt△ABC中,∠BAC=90°,斜边BC上的高AD=8,sin B=,则AC的长为 .
11. (2024·上海)在 ABCD中,∠ABC是锐角,将CD沿直线l翻折至AB所在直线,点C、D的对应点分别为C'、D'.若AC'∶AB∶BC=1∶3∶7,则cos∠ABC的值为 .
12. (2023·深圳)如图,在菱形ABCD中,cosA=,过点C作CE⊥AB,交AB的延长线于点E,过点E作EF⊥AD,交AD于点F.若S菱形ABCD=24,求EF·BC的值.
第12题
13. (2024·遂宁)小明的书桌上有一个L型台灯,灯柱AB高40cm,他发现当灯带BC与水平线BM的夹角为9°时(如图①),灯带的直射宽度DE(BD⊥BC,CE⊥BC)为35cm,但此时灯的直射宽度不够,当他把灯带调整到与水平线夹角为30°时(如图②),直射宽度刚好合适,求此时台灯最高点C到桌面的距离(精确到0.1cm,参考数据:sin9°≈0.16,cos9°≈0.99,sin30°=0.5,cos30°≈0.87).
7.2 正弦、余弦
第1课时 正弦、余弦的概念
1. D 2. A 3. 4. 0.57 0.81 5. ①②
6. 设正方形ABCD的边长为4a.∵ BE=3AE,∴ AE=a,BE=3a.∵ 四边形ABCD是正方形,∴ ∠A=∠B=∠D=90°.在Rt△BCE中,BE=3a,BC=4a,∴ 由勾股定理,得EC==5a.∵ M是AD的中点,∴ AM=MD=AD=2a.∴ 在Rt△AEM中,由勾股定理,得EM==a,在Rt△CDM中,由勾股定理,得MC==2a.∴ EM2+MC2=EC2.∴ ∠EMC=90°.∴ 在Rt△CEM中,tan∠ECM==,sin∠ECM==,cos∠ECM==
7. B 8. C 9. 10. 或
11. (1) ∵ AD⊥BC,AB=10,AD=6,∴ 由勾股定理,得BD===8.∵ 在Rt△ADC中,tan∠ACB=,tan∠ACB=1,∴ CD=AD=6.∴ BC=BD+CD=8+6=14 (2) ∵ AE是边BC上的中线,∴ CE=BC=7.∴ DE=CE-CD=7-6=1.∵ AD⊥BC,∴ 由勾股定理,得AE===.∴ 在Rt△ADE中,sin∠DAE===
12. (1) 直线AB与☉O相切 理由:连接OD.∵ OC=OD,∴ ∠OCD=∠ODC.∴ ∠BOD=∠OCD+∠ODC=2∠BCD.∴ ∠BCD=∠BOD.∵ ∠BCD=∠A,∴ ∠BOD=∠A.∵ 在△ABC中,∠ACB=90°,∴ ∠A+∠B=90°.∴ ∠BOD+∠B=90°.∴ 在△ODB中,∠BDO=90°.∴ OD⊥AB.∵ OD是☉O的半径,∴ 直线AB与☉O相切. (2) ∵ 在Rt△ODB中,cosB==,∴ 设BD=4x(x>0),则OB=5x.∴ 由勾股定理,得OD==3x.∵ OD=OC=3,∴ 3x=3,解得x=1.∴ OB=5x=5.∴ BC=OB+OC=8. ∵ 在Rt△ACB中,cosB==,∴ AB=10.∴ 由勾股定理,得AC==6
第2课时 正弦、余弦的计算与应用
1. C 2. B 3. (1) 0.8156 (2) 4. ①③⑤ 5. sin10°
7. A 8. 9.
10. 10 解析:先利用同角的余角相等说明∠B=∠DAC,即sin B=sin ∠DAC,即=,由此可设DC=3k(k>0),则AC=5k,在Rt△ADC中,根据勾股定理,得AD=4k.∵ AD=8,∴ 4k=8,解得k=2.∴ AC=5×2=10.
11. 或 解析:分点C'在线段AB上和点C'在BA的延长线上两种情况讨论.
12. ∵ 四边形ABCD是菱形,∴ AD∥BC,AB=BC.∴ ∠CBE=∠A.∵ cosA=,∴ cos∠CBE=.∵ CE⊥AB,∴ ∠CEB=90°.∴ 在Rt△CEB中,cos∠CBE==.∴ BE=BC.∴ AE=AB+BE=AB+BC=AB+AB=AB.∵ EF⊥AD,CE⊥AB,∴ ∠AFE=∠BEC=90°.∴ △AFE∽△BEC.∴ =.∴ EF·BC=AE·CE=AB·CE=S菱形ABCD=×24=32
13. 在题图①中,∵ DB⊥BC,EC⊥BC,∴ BD∥EC.∵ BM∥DE,∴ 四边形BDEM是平行四边形.∴ BM=DE=35cm.∵ CE⊥BC,∴ 在Rt△BCM中,BC=BM·cos9°≈35×0.99=34.65(cm).如图,过点C作CK⊥AE'于点K,交BM于点J,则四边形BAKJ为矩形.∴ BA=JK=40cm,∠BJK=∠BJC=90°.∴ 在Rt△BJC中,CJ=BC·sin30°=17.325cm.∴ CK=CJ+JK=17.325+40≈57.3(cm).∴ 台灯最高点C到桌面的距离约为57.3cm
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
