7.3 特殊角的三角函数 练习( 含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 7.3 特殊角的三角函数 练习( 含答案) 2024-2025学年数学苏科版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 133.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 15:54:17 | ||
图片预览

文档简介
7.3 特殊角的三角函数
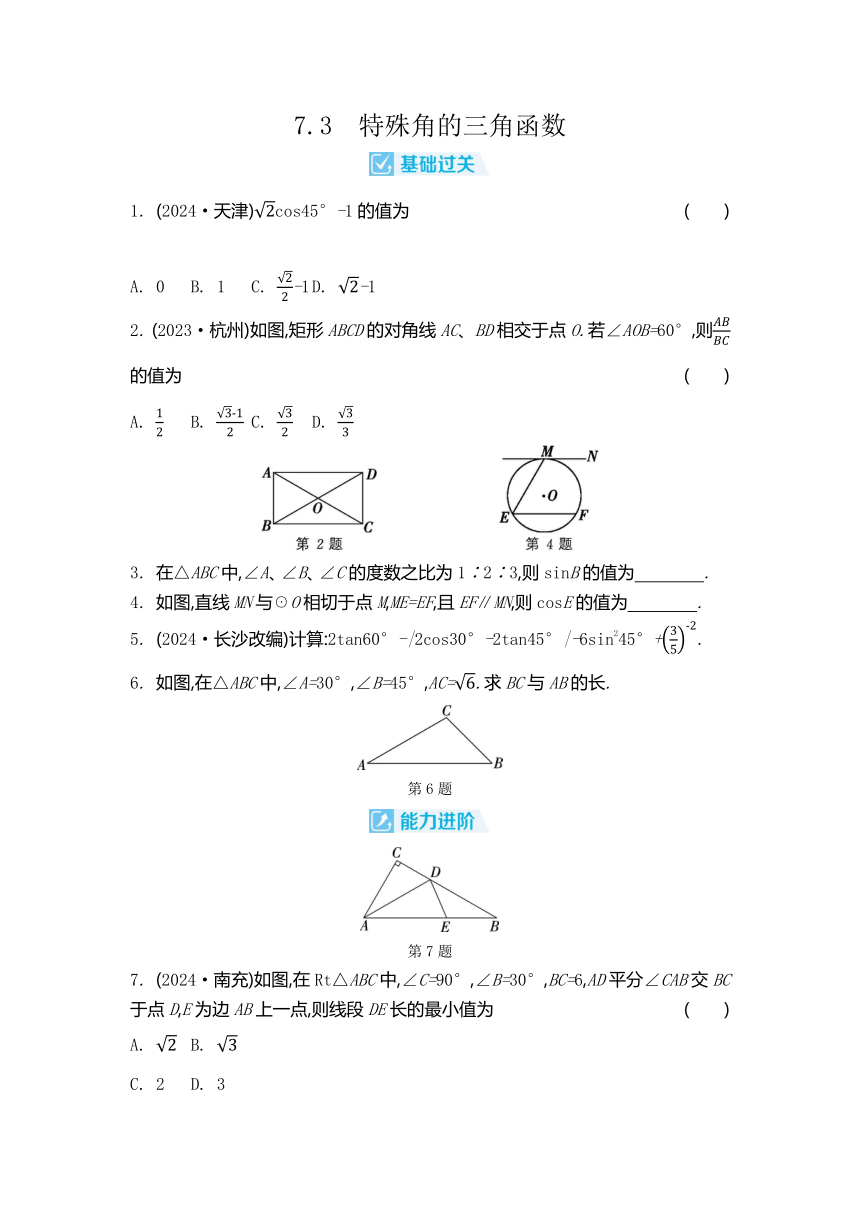
1. (2024·天津)cos45°-1的值为 ( )
A. 0 B. 1 C. -1 D. -1
2. (2023·杭州)如图,矩形ABCD的对角线AC、BD相交于点O.若∠AOB=60°,则的值为 ( )
A. B. C. D.
3. 在△ABC中,∠A、∠B、∠C的度数之比为1∶2∶3,则sinB的值为 .
4. 如图,直线MN与☉O相切于点M,ME=EF,且EF∥MN,则cosE的值为 .
5. (2024·长沙改编)计算:2tan60°-|2cos30°-2tan45°|-6sin245°+.
6. 如图,在△ABC中,∠A=30°,∠B=45°,AC=.求BC与AB的长.
第6题
第7题
7. (2024·南充)如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=6,AD平分∠CAB交BC于点D,E为边AB上一点,则线段DE长的最小值为 ( )
A. B.
C. 2 D. 3
8. 已知关于x的一元二次方程2x2+4sinα·x+1=0有两个相等的实数根,则锐角α的度数为 ( )
A. 30° B. 45° C. 60° D. 75°
9. (1) 已知α是锐角,cos2α=,则α的度数为 ;
(2) 在△ABC中,∠C=90°,tan(A-15°)=,则cosB的值为 .
10. 如图,在Rt△ABC中,∠BCA=90°,CD⊥AB,垂足为D.若AD=2,CD=2,则∠B= °,sinA的值为 .
11. (2023·宁夏)将一副三角尺和一把宽度为2的直尺按如图所示的方式摆放,先把60°和45°角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上,这两把三角尺的斜边分别交直尺上沿于A、B两点,则AB的长为 .
12. 一般地,当α、β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sinα·cosβ+cosα·sinβ;sin(α-β)=sinα·cosβ-cosα·sinβ.例如:sin75°=sin(45°+30°)=sin45°·cos30°+cos45°·sin30°=×+×=.类似地,请求出sin15°的值.
13. (2024·湖北)如图,在Rt△ABC中,∠ACB=90°,点E在AC上,以CE为直径的☉O经过AB上的点D,与OB交于点F,且BD=BC.
(1) 求证:AB是☉O的切线;
(2) 若AD=,AE=1,求的长.
第13题
7.3 特殊角的三角函数
1. A 2. D 3. 4.
5. 原式=2×-2×-2×1-6×2+=2-2+-3+=3-
6. 过点C作CD⊥AB于点D.∵ ∠A=30°,AC=,cosA=cos30°==,∴ AD=.∵ sinA=sin30°==,∴ CD=.∵ tanB=tan45°==1,∴ BD=.∴ AB=AD+BD=.在Rt△BCD中,由勾股定理,得BC==
7. C 8. B 9. (1) 30° (2) 10. 30 11. 2-2
12. sin15°=sin(45°-30°)=sin45°·cos30°-cos45°·sin30°=×-×=
13. (1) 连接OD.在△OBD和△OBC中,∴ △OBD≌△OBC.∴ ∠ODB=∠OCB=90°.∴ OD⊥AB.∵ OD是☉O的半径,∴ AB是☉O的切线 (2) 设☉O的半径为R,则OD=R,AO=AE+OE=1+R.∵ 在Rt△OAD中,AD2+OD2=AO2,AD=,∴ ()2+R2=(1+R)2,解得R=1.∴ OD=1.∴ tan∠AOD==.∴ ∠AOD=60°.∴ ∠COD=180°-∠AOD=120°.由(1),知△OBD≌△OBC,∴ ∠BOD=∠BOC=∠COD=60°.∴ 的长==
1. (2024·天津)cos45°-1的值为 ( )
A. 0 B. 1 C. -1 D. -1
2. (2023·杭州)如图,矩形ABCD的对角线AC、BD相交于点O.若∠AOB=60°,则的值为 ( )
A. B. C. D.
3. 在△ABC中,∠A、∠B、∠C的度数之比为1∶2∶3,则sinB的值为 .
4. 如图,直线MN与☉O相切于点M,ME=EF,且EF∥MN,则cosE的值为 .
5. (2024·长沙改编)计算:2tan60°-|2cos30°-2tan45°|-6sin245°+.
6. 如图,在△ABC中,∠A=30°,∠B=45°,AC=.求BC与AB的长.
第6题
第7题
7. (2024·南充)如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=6,AD平分∠CAB交BC于点D,E为边AB上一点,则线段DE长的最小值为 ( )
A. B.
C. 2 D. 3
8. 已知关于x的一元二次方程2x2+4sinα·x+1=0有两个相等的实数根,则锐角α的度数为 ( )
A. 30° B. 45° C. 60° D. 75°
9. (1) 已知α是锐角,cos2α=,则α的度数为 ;
(2) 在△ABC中,∠C=90°,tan(A-15°)=,则cosB的值为 .
10. 如图,在Rt△ABC中,∠BCA=90°,CD⊥AB,垂足为D.若AD=2,CD=2,则∠B= °,sinA的值为 .
11. (2023·宁夏)将一副三角尺和一把宽度为2的直尺按如图所示的方式摆放,先把60°和45°角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上,这两把三角尺的斜边分别交直尺上沿于A、B两点,则AB的长为 .
12. 一般地,当α、β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sinα·cosβ+cosα·sinβ;sin(α-β)=sinα·cosβ-cosα·sinβ.例如:sin75°=sin(45°+30°)=sin45°·cos30°+cos45°·sin30°=×+×=.类似地,请求出sin15°的值.
13. (2024·湖北)如图,在Rt△ABC中,∠ACB=90°,点E在AC上,以CE为直径的☉O经过AB上的点D,与OB交于点F,且BD=BC.
(1) 求证:AB是☉O的切线;
(2) 若AD=,AE=1,求的长.
第13题
7.3 特殊角的三角函数
1. A 2. D 3. 4.
5. 原式=2×-2×-2×1-6×2+=2-2+-3+=3-
6. 过点C作CD⊥AB于点D.∵ ∠A=30°,AC=,cosA=cos30°==,∴ AD=.∵ sinA=sin30°==,∴ CD=.∵ tanB=tan45°==1,∴ BD=.∴ AB=AD+BD=.在Rt△BCD中,由勾股定理,得BC==
7. C 8. B 9. (1) 30° (2) 10. 30 11. 2-2
12. sin15°=sin(45°-30°)=sin45°·cos30°-cos45°·sin30°=×-×=
13. (1) 连接OD.在△OBD和△OBC中,∴ △OBD≌△OBC.∴ ∠ODB=∠OCB=90°.∴ OD⊥AB.∵ OD是☉O的半径,∴ AB是☉O的切线 (2) 设☉O的半径为R,则OD=R,AO=AE+OE=1+R.∵ 在Rt△OAD中,AD2+OD2=AO2,AD=,∴ ()2+R2=(1+R)2,解得R=1.∴ OD=1.∴ tan∠AOD==.∴ ∠AOD=60°.∴ ∠COD=180°-∠AOD=120°.由(1),知△OBD≌△OBC,∴ ∠BOD=∠BOC=∠COD=60°.∴ 的长==
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
