7.5 解直角三角形 练习(2课时、含答案)2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 7.5 解直角三角形 练习(2课时、含答案)2024-2025学年数学苏科版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 252.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 15:55:01 | ||
图片预览


文档简介
7.5 解直角三角形
第1课时 解直角三角形
1.
在一个直角三角形中,已知下列条件:① 两条边的长度;② 两个锐角的度数;③ 一个锐角的度数和一条边的长度.利用上述条件中的一个,能解这个直角三角形的有 ( )
A. ①② B. ①③ C. ②③ D. ①②③
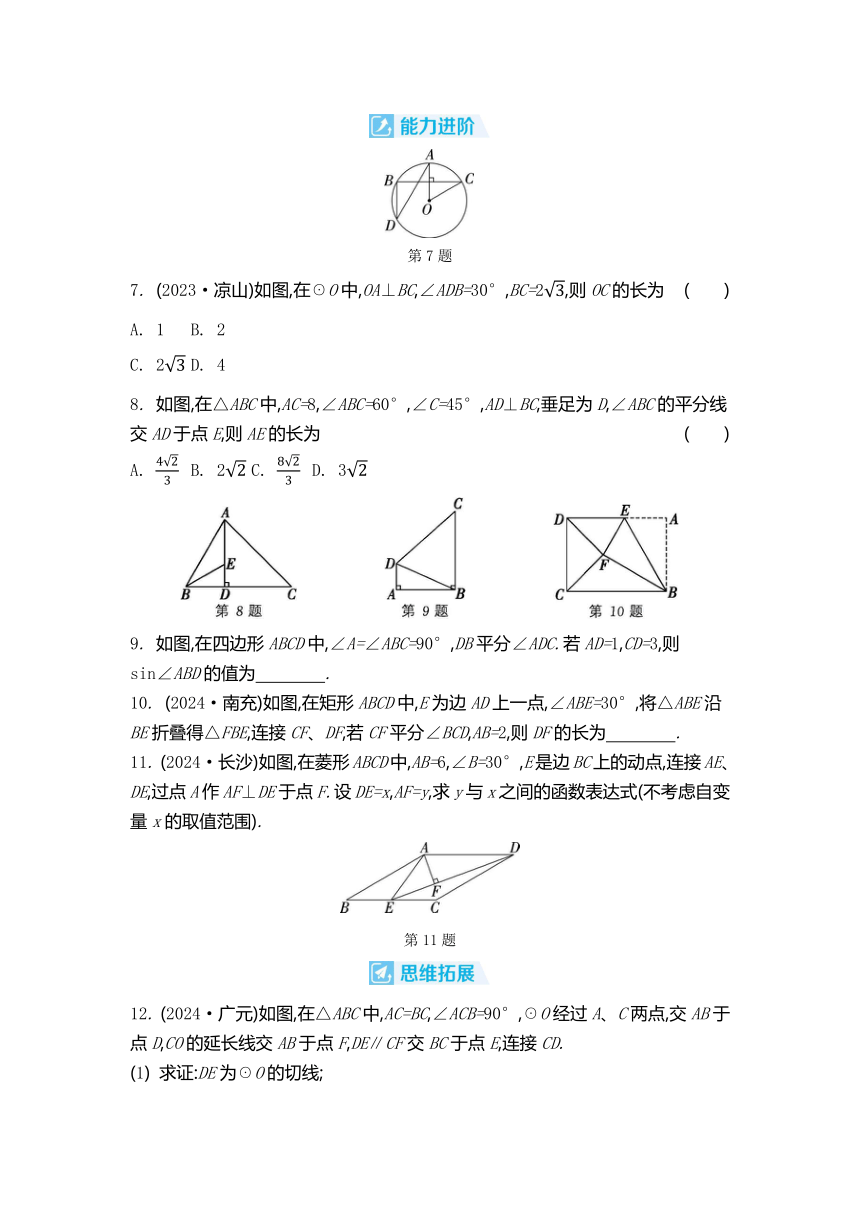
2. 如图,在Rt△ACB中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cos A=,则BD的长为 ( )
A. B. C. D. 4
3. 如图,在Rt△ABC中,∠C=90°,∠B=45°,AB=8,则BC的长为 .
4. 如图,在△ABC中,BC=12,tan A=,∠B=30°,则AC的长为 ,AB的长为 .
5. (2024·临夏)如图,在△ABC中,AB=AC=2,∠BAC=120°,将△ABC沿其底边中线AD向下平移到△A'B'C'的位置,AA'=AD,则平移前后两个三角形重叠部分(涂色部分)的面积是 .
6. 在Rt△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,请根据下面的条件解直角三角形.
(1) a=2,c=7(角度精确到0.01°); (2) ∠B=30°,a-b=3-3.
第7题
7. (2023·凉山)如图,在☉O中,OA⊥BC,∠ADB=30°,BC=2,则OC的长为 ( )
A. 1 B. 2
C. 2 D. 4
8. 如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为 ( )
A. B. 2 C. D. 3
9. 如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分∠ADC.若AD=1,CD=3,则sin∠ABD的值为 .
10. (2024·南充)如图,在矩形ABCD中,E为边AD上一点,∠ABE=30°,将△ABE沿BE折叠得△FBE,连接CF、DF,若CF平分∠BCD,AB=2,则DF的长为 .
11. (2024·长沙)如图,在菱形ABCD中,AB=6,∠B=30°,E是边BC上的动点,连接AE、DE,过点A作AF⊥DE于点F.设DE=x,AF=y,求y与x之间的函数表达式(不考虑自变量x的取值范围).
第11题
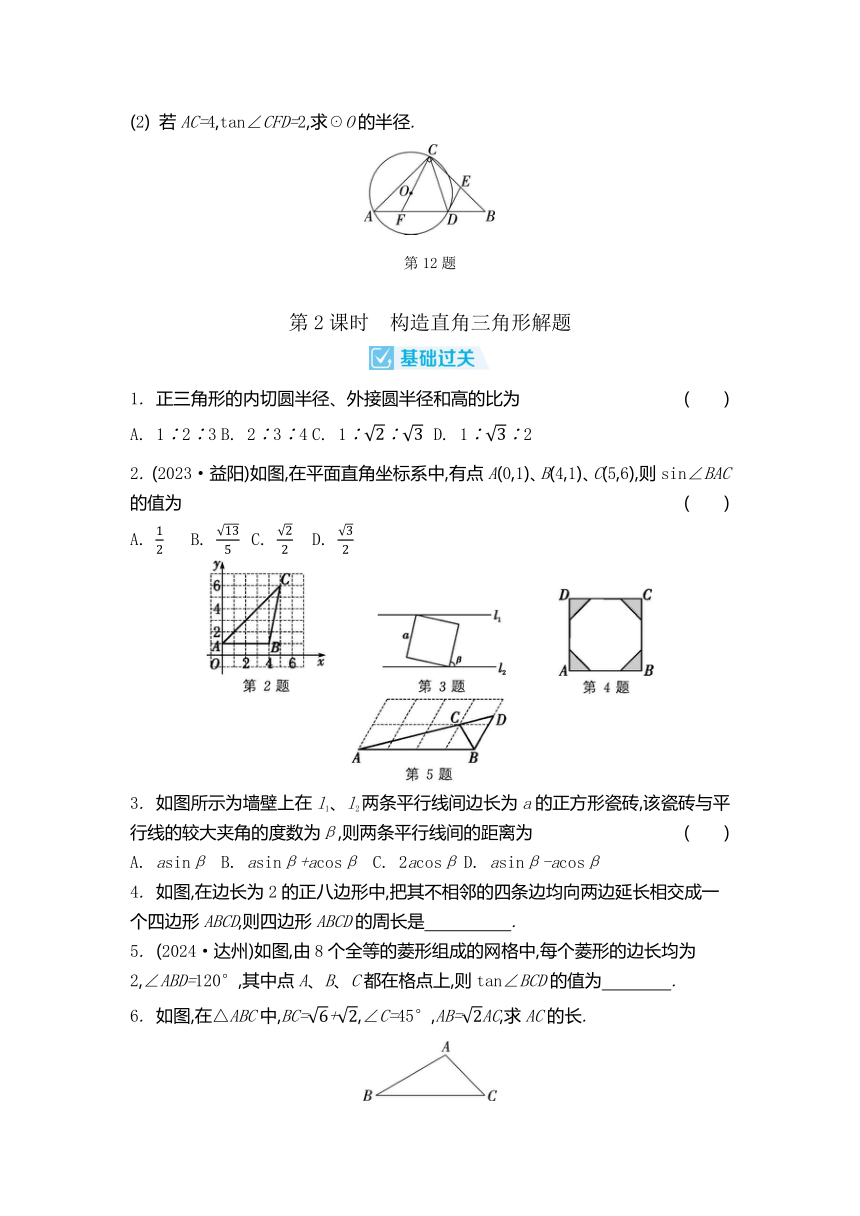
12. (2024·广元)如图,在△ABC中,AC=BC,∠ACB=90°,☉O经过A、C两点,交AB于点D,CO的延长线交AB于点F,DE∥CF交BC于点E,连接CD.
(1) 求证:DE为☉O的切线;
(2) 若AC=4,tan∠CFD=2,求☉O的半径.
第12题
第2课时 构造直角三角形解题
1. 正三角形的内切圆半径、外接圆半径和高的比为 ( )
A. 1∶2∶3 B. 2∶3∶4 C. 1∶∶ D. 1∶∶2
2. (2023·益阳)如图,在平面直角坐标系中,有点A(0,1)、B(4,1)、C(5,6),则sin∠BAC的值为 ( )
A. B. C. D.
3. 如图所示为墙壁上在l1、l2两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角的度数为β,则两条平行线间的距离为 ( )
A. asinβ B. asinβ+acosβ C. 2acosβ D. asinβ-acosβ
4. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 .
5. (2024·达州)如图,由8个全等的菱形组成的网格中,每个菱形的边长均为2,∠ABD=120°,其中点A、B、C都在格点上,则tan∠BCD的值为 .
6. 如图,在△ABC中,BC=+,∠C=45°,AB=AC,求AC的长.
第6题
7. 若正方形的外接圆半径为2,则其内切圆半径为 ( )
A. B. 2 C. D. 1
第8题
8. 如图,△ABC内接于☉O.若BC=2,tanA=,则☉O的直径为 ( )
A. 7 B.
C. D. 5
9. 如图,△ABC内接于☉O,AO=2,BC=2,则∠BAC的度数为 .
10. 把两把同样大的含45°角的三角尺按如图所示的方式放置,其中一把三角尺的锐角顶点与另一把三角尺的直角顶点重合于点A,且另三个锐角顶点B、C、D在同一条直线上.若AB=,则CD的长为 .
11. (2024·贵州)如图,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.如果sin∠EAF=,AE=5,那么AB的长为 .
12. 如图,在正方形方格纸中,每个小正方形的边长都为1,点A、B、C、D都在格点处,BA与CD相交于点P,则cos∠APC的值为 .
13. 如图,△ABC的顶点都在小正方形网格的格点上,求∠BAC的三个三角函数值.
第13题
14. (2024·赤峰)如图,在△ABC中,∠ACB=90°,AC=BC,☉O经过B、C两点,与斜边AB交于点E,连接CO并延长,交AB于点M,交☉O于点D,过点E作EF∥CD,交AC于点F.
(1) 求证:EF是☉O的切线;
(2) 若BM=4,tan∠BCD=,求OM的长.
第14题
7.5 解直角三角形
第1课时 解直角三角形
1. B
2. C 解析:在Rt△ACB中,利用cos A==,可求出AB=5,结合勾股定理,得BC=3.在Rt△DCB中,利用cos ∠DBC=cos A==,可求出BD的长.
3. 4 4. 10 8+6 5.
6. (1) 根据勾股定理,得b==5.∵ sinA==,∴ ∠A≈44.42°.∵ sinB==,∴ ∠B≈45.58°.∴ ∠A≈44.42°,∠B≈45.58°,b=5 (2) ∠A=90°-∠B=60°.∵ tanB==,∴ b=a.∵ a-b=3-3,∴ a=3,b=3.∴ c==6
7. B 8. C 9. 10.
11. 过点D作DH⊥BC,交BC的延长线于点H.∵ 四边形ABCD是菱形,AB=6,∴ AB∥CD,AD∥BC,AB=CD=AD=6.∴ ∠DCH=∠B=30°,∠ADF=∠DEH.∴ 在Rt△DHC中,DH=CD·sin30°=6×=3.∵ AF⊥DE,DH⊥BC,∴ ∠AFD=∠DHE=90°.∴ △ADF∽△DEH.∴ =.∴ =.∴ y=
12. (1) 如图,连接OD.∵ AC=BC,∴ ∠A=∠B.∵ ∠ACB=90°,∴ ∠A=45°.∵ =,∴ ∠COD=2∠A=90°.∵ DE∥CF,∴ ∠COD+∠EDO=180°.∴ ∠EDO=90°,即OD⊥DE.∵ OD是☉O的半径,∴ DE为☉O的切线 (2) 如图,过点C作CH⊥AB于点H.∵ 在Rt△AHC中,sinA=,AC=4,∴ CH=4×sin45°=2.∵ 在Rt△CHF中,tan∠CFD==2,∴ FH=.∴ 在Rt△CHF中,由勾股定理,得CF===.∵ 在Rt△ODF中,tan∠CFD====2,∴ OD=.∴ ☉O的半径为
第2课时 构造直角三角形解题
1. A 2. C 3. B 4. 8+8 5. 2
6. 过点A作AD⊥BC,垂足为D.设AC=x,则AB=x.∵ 在Rt△ACD中,∠C=45°,∴ AD=AC·sin45°=x,CD=AC·cos45°=x.∴ 在Rt△ABD中,由勾股定理,得BD==x.∵ BC=+,∴ BD+CD=+,即x+x=+,解得x=2.∴ AC的长为2
7. A 8. C 9. 60° 10. -1 11.
12. 解析:如图,把BA向上平移一格到DE,连接CE.∴ DE∥BA.∴ ∠APC=∠EDC.在△DCE中,EC==,DC==2,DE==5.∵ EC2+DC2=DE2,∴ △DCE为直角三角形,∠DCE=90°.∴ cos∠APC=cos∠EDC==.
13. 过点C作CF⊥AB于点F.设小正方形的边长为a(a>0),则BC=2a,点A到BC的距离h=2a.由勾股定理,得AB==2a,AC==2a.由三角形的面积公式,得AB·CF=BC·h,即×2a×CF=×2a×2a,解得CF=a.在Rt△AFC中,由勾股定理,得AF==a.∴ tan∠BAC==,sin∠BAC==,cos∠BAC==
14. (1) 如图,连接OE.∵ ∠ACB=90°,AC=BC,∴ ∠A=∠ABC=45°.∴ ∠COE=2∠ABC=90°.∵ EF∥CD,∴ ∠COE+∠FEO=180°.∴ ∠FEO=90°.∵ OE是☉O的半径,∴ EF是☉O的切线 (2) 如图,连接BD,过点M作MH⊥BC于点H,则△BMH是等腰直角三角形.∵ 在Rt△BHM中,BM=4,∴ BH=MH=BM·sin45°=4×=4.∵ 在Rt△CHM中,tan∠BCD==,∴ CH=2MH=8.∴ 由勾股定理,得CM==4,CB=CH+BH=12.∵ CD是☉O的直径,∴ ∠DBC=90°.∴ BD⊥BC.∴ MH∥BD.∴ =,即=.∴ DM=2.∴ OD=CD=(CM+DM)=3.∴ OM=OD-DM=
第1课时 解直角三角形
1.
在一个直角三角形中,已知下列条件:① 两条边的长度;② 两个锐角的度数;③ 一个锐角的度数和一条边的长度.利用上述条件中的一个,能解这个直角三角形的有 ( )
A. ①② B. ①③ C. ②③ D. ①②③
2. 如图,在Rt△ACB中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cos A=,则BD的长为 ( )
A. B. C. D. 4
3. 如图,在Rt△ABC中,∠C=90°,∠B=45°,AB=8,则BC的长为 .
4. 如图,在△ABC中,BC=12,tan A=,∠B=30°,则AC的长为 ,AB的长为 .
5. (2024·临夏)如图,在△ABC中,AB=AC=2,∠BAC=120°,将△ABC沿其底边中线AD向下平移到△A'B'C'的位置,AA'=AD,则平移前后两个三角形重叠部分(涂色部分)的面积是 .
6. 在Rt△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,请根据下面的条件解直角三角形.
(1) a=2,c=7(角度精确到0.01°); (2) ∠B=30°,a-b=3-3.
第7题
7. (2023·凉山)如图,在☉O中,OA⊥BC,∠ADB=30°,BC=2,则OC的长为 ( )
A. 1 B. 2
C. 2 D. 4
8. 如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为 ( )
A. B. 2 C. D. 3
9. 如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分∠ADC.若AD=1,CD=3,则sin∠ABD的值为 .
10. (2024·南充)如图,在矩形ABCD中,E为边AD上一点,∠ABE=30°,将△ABE沿BE折叠得△FBE,连接CF、DF,若CF平分∠BCD,AB=2,则DF的长为 .
11. (2024·长沙)如图,在菱形ABCD中,AB=6,∠B=30°,E是边BC上的动点,连接AE、DE,过点A作AF⊥DE于点F.设DE=x,AF=y,求y与x之间的函数表达式(不考虑自变量x的取值范围).
第11题
12. (2024·广元)如图,在△ABC中,AC=BC,∠ACB=90°,☉O经过A、C两点,交AB于点D,CO的延长线交AB于点F,DE∥CF交BC于点E,连接CD.
(1) 求证:DE为☉O的切线;
(2) 若AC=4,tan∠CFD=2,求☉O的半径.
第12题
第2课时 构造直角三角形解题
1. 正三角形的内切圆半径、外接圆半径和高的比为 ( )
A. 1∶2∶3 B. 2∶3∶4 C. 1∶∶ D. 1∶∶2
2. (2023·益阳)如图,在平面直角坐标系中,有点A(0,1)、B(4,1)、C(5,6),则sin∠BAC的值为 ( )
A. B. C. D.
3. 如图所示为墙壁上在l1、l2两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角的度数为β,则两条平行线间的距离为 ( )
A. asinβ B. asinβ+acosβ C. 2acosβ D. asinβ-acosβ
4. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 .
5. (2024·达州)如图,由8个全等的菱形组成的网格中,每个菱形的边长均为2,∠ABD=120°,其中点A、B、C都在格点上,则tan∠BCD的值为 .
6. 如图,在△ABC中,BC=+,∠C=45°,AB=AC,求AC的长.
第6题
7. 若正方形的外接圆半径为2,则其内切圆半径为 ( )
A. B. 2 C. D. 1
第8题
8. 如图,△ABC内接于☉O.若BC=2,tanA=,则☉O的直径为 ( )
A. 7 B.
C. D. 5
9. 如图,△ABC内接于☉O,AO=2,BC=2,则∠BAC的度数为 .
10. 把两把同样大的含45°角的三角尺按如图所示的方式放置,其中一把三角尺的锐角顶点与另一把三角尺的直角顶点重合于点A,且另三个锐角顶点B、C、D在同一条直线上.若AB=,则CD的长为 .
11. (2024·贵州)如图,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.如果sin∠EAF=,AE=5,那么AB的长为 .
12. 如图,在正方形方格纸中,每个小正方形的边长都为1,点A、B、C、D都在格点处,BA与CD相交于点P,则cos∠APC的值为 .
13. 如图,△ABC的顶点都在小正方形网格的格点上,求∠BAC的三个三角函数值.
第13题
14. (2024·赤峰)如图,在△ABC中,∠ACB=90°,AC=BC,☉O经过B、C两点,与斜边AB交于点E,连接CO并延长,交AB于点M,交☉O于点D,过点E作EF∥CD,交AC于点F.
(1) 求证:EF是☉O的切线;
(2) 若BM=4,tan∠BCD=,求OM的长.
第14题
7.5 解直角三角形
第1课时 解直角三角形
1. B
2. C 解析:在Rt△ACB中,利用cos A==,可求出AB=5,结合勾股定理,得BC=3.在Rt△DCB中,利用cos ∠DBC=cos A==,可求出BD的长.
3. 4 4. 10 8+6 5.
6. (1) 根据勾股定理,得b==5.∵ sinA==,∴ ∠A≈44.42°.∵ sinB==,∴ ∠B≈45.58°.∴ ∠A≈44.42°,∠B≈45.58°,b=5 (2) ∠A=90°-∠B=60°.∵ tanB==,∴ b=a.∵ a-b=3-3,∴ a=3,b=3.∴ c==6
7. B 8. C 9. 10.
11. 过点D作DH⊥BC,交BC的延长线于点H.∵ 四边形ABCD是菱形,AB=6,∴ AB∥CD,AD∥BC,AB=CD=AD=6.∴ ∠DCH=∠B=30°,∠ADF=∠DEH.∴ 在Rt△DHC中,DH=CD·sin30°=6×=3.∵ AF⊥DE,DH⊥BC,∴ ∠AFD=∠DHE=90°.∴ △ADF∽△DEH.∴ =.∴ =.∴ y=
12. (1) 如图,连接OD.∵ AC=BC,∴ ∠A=∠B.∵ ∠ACB=90°,∴ ∠A=45°.∵ =,∴ ∠COD=2∠A=90°.∵ DE∥CF,∴ ∠COD+∠EDO=180°.∴ ∠EDO=90°,即OD⊥DE.∵ OD是☉O的半径,∴ DE为☉O的切线 (2) 如图,过点C作CH⊥AB于点H.∵ 在Rt△AHC中,sinA=,AC=4,∴ CH=4×sin45°=2.∵ 在Rt△CHF中,tan∠CFD==2,∴ FH=.∴ 在Rt△CHF中,由勾股定理,得CF===.∵ 在Rt△ODF中,tan∠CFD====2,∴ OD=.∴ ☉O的半径为
第2课时 构造直角三角形解题
1. A 2. C 3. B 4. 8+8 5. 2
6. 过点A作AD⊥BC,垂足为D.设AC=x,则AB=x.∵ 在Rt△ACD中,∠C=45°,∴ AD=AC·sin45°=x,CD=AC·cos45°=x.∴ 在Rt△ABD中,由勾股定理,得BD==x.∵ BC=+,∴ BD+CD=+,即x+x=+,解得x=2.∴ AC的长为2
7. A 8. C 9. 60° 10. -1 11.
12. 解析:如图,把BA向上平移一格到DE,连接CE.∴ DE∥BA.∴ ∠APC=∠EDC.在△DCE中,EC==,DC==2,DE==5.∵ EC2+DC2=DE2,∴ △DCE为直角三角形,∠DCE=90°.∴ cos∠APC=cos∠EDC==.
13. 过点C作CF⊥AB于点F.设小正方形的边长为a(a>0),则BC=2a,点A到BC的距离h=2a.由勾股定理,得AB==2a,AC==2a.由三角形的面积公式,得AB·CF=BC·h,即×2a×CF=×2a×2a,解得CF=a.在Rt△AFC中,由勾股定理,得AF==a.∴ tan∠BAC==,sin∠BAC==,cos∠BAC==
14. (1) 如图,连接OE.∵ ∠ACB=90°,AC=BC,∴ ∠A=∠ABC=45°.∴ ∠COE=2∠ABC=90°.∵ EF∥CD,∴ ∠COE+∠FEO=180°.∴ ∠FEO=90°.∵ OE是☉O的半径,∴ EF是☉O的切线 (2) 如图,连接BD,过点M作MH⊥BC于点H,则△BMH是等腰直角三角形.∵ 在Rt△BHM中,BM=4,∴ BH=MH=BM·sin45°=4×=4.∵ 在Rt△CHM中,tan∠BCD==,∴ CH=2MH=8.∴ 由勾股定理,得CM==4,CB=CH+BH=12.∵ CD是☉O的直径,∴ ∠DBC=90°.∴ BD⊥BC.∴ MH∥BD.∴ =,即=.∴ DM=2.∴ OD=CD=(CM+DM)=3.∴ OM=OD-DM=
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
