7.6 用锐角三角函数解决问题 练习(3课时、含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 7.6 用锐角三角函数解决问题 练习(3课时、含答案) 2024-2025学年数学苏科版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 440.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 15:58:14 | ||
图片预览




文档简介
7.6 用锐角三角函数解决问题
第1课时 与坡度和坡角有关的问题
1.
(2024·威海改编)如图,某商场有一自动扶梯,其坡角为28°,高为7米.用计算器求AB的长,下列按键顺序正确的是 ( )
A. 7 × sin 2 8 = B. 7 ÷ sin 2 8 =
C. 7 × tan 2 8 = D. 7 ÷ tan 2 8 =
2. 已知某河堤的横截面为梯形ABCD,上底长为4m,堤高为6m,斜坡AD的坡度为1∶3,斜坡CB的坡角为45°,则河堤横截面的下底长为 ( )
A. 28m B. 12m C. 60m D. 24m
3. 一条上山直道的坡度为1∶7,沿这条直道上山,每前进100m所上升的高度为 m.
4. 如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB的长为26m,斜坡AB的坡比为12∶5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.若改造时保持坡脚A不动,则坡顶B沿BC至少向右移 m,才能确保山体不滑坡(参考数据:tan 50°≈1.2).
5. (2023·仙桃)为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形ABCD,斜面坡度i=3∶4是指坡面的铅直高度AF与水平宽度BF的比.已知斜坡CD的长为20m,∠C=18°,求斜坡AB的长(精确到0.1m,参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32).
第5题
第6题
6. 如图,小明去爬山,在山脚看山顶的角度为30°,小明在坡比为5∶12的山坡上走1300m,此时小明看山顶的角度为60°,山高为 ( )
A. (600-250)m B. (600-250)m
C. (350+350)m D. 500m
第7题
7. (2024·眉山改编)如图,坡面CD的坡度为1∶,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线的夹角成60°时,测得小树在坡顶平地上的树影BC=3m,在斜坡上的树影CD=m,则小树AB的高是 m.
8. 日照间距系数反映了房屋日照情况.如图①,当前、后房屋都朝向正南时,日照间距系数=L∶(H-H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面的高度.如图②,山坡EF朝北,EF的长为15m,坡度i=1∶0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到点E的距离为4m.
(1) 求山坡EF的水平宽度FG;
(2) 欲在楼房AB正北侧山脚的平地FN上建一楼房CD,该楼房底层窗台P处至地面C处的高度为0.9m,要使该楼房的日照间距系数不低于1.25,底部C距F处至少多远
第8题
9. 如图,某仓储中心有一斜坡AB,其坡度为i=1∶2,顶部A处的高AC为4m,点B、C在同一水平地面上.
(1) 求斜坡AB的水平宽度BC.
(2) 矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m.将该货柜沿斜坡向上运送,当BF=3.5m时,求点D到地面的高(精确到0.1m,参考数据:≈2.236).
第9题
第2课时 与旋转等有关的问题
1. 某停车场入口栏杆如图所示,栏杆从水平位置AB绕点O旋转到CD的位置,AO=a.若栏杆的旋转角为∠AOD=41°,则栏杆端点A上升的垂直距离为 ( )
A. asin41° B. acos41° C. D. atan41°
2. 如图所示为一个小孩荡秋千的示意图,秋千链子OA的长度为2m,当秋千向两边摆动时,两边摆动的角度均为30°,则秋千摆动至最高位置与最低位置时的高度差为 ( )
A. m B. m C. (2-)m D. (2-)m
3. (2024·兰州)单摆是一种能够产生往复摆动的装置.如图,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,BD⊥OA,∠BOA=64°,BD=20.5cm;当摆球摆动至点C时,∠COA=37°,CE⊥OA.由此可得ED的长约为 cm(精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05).
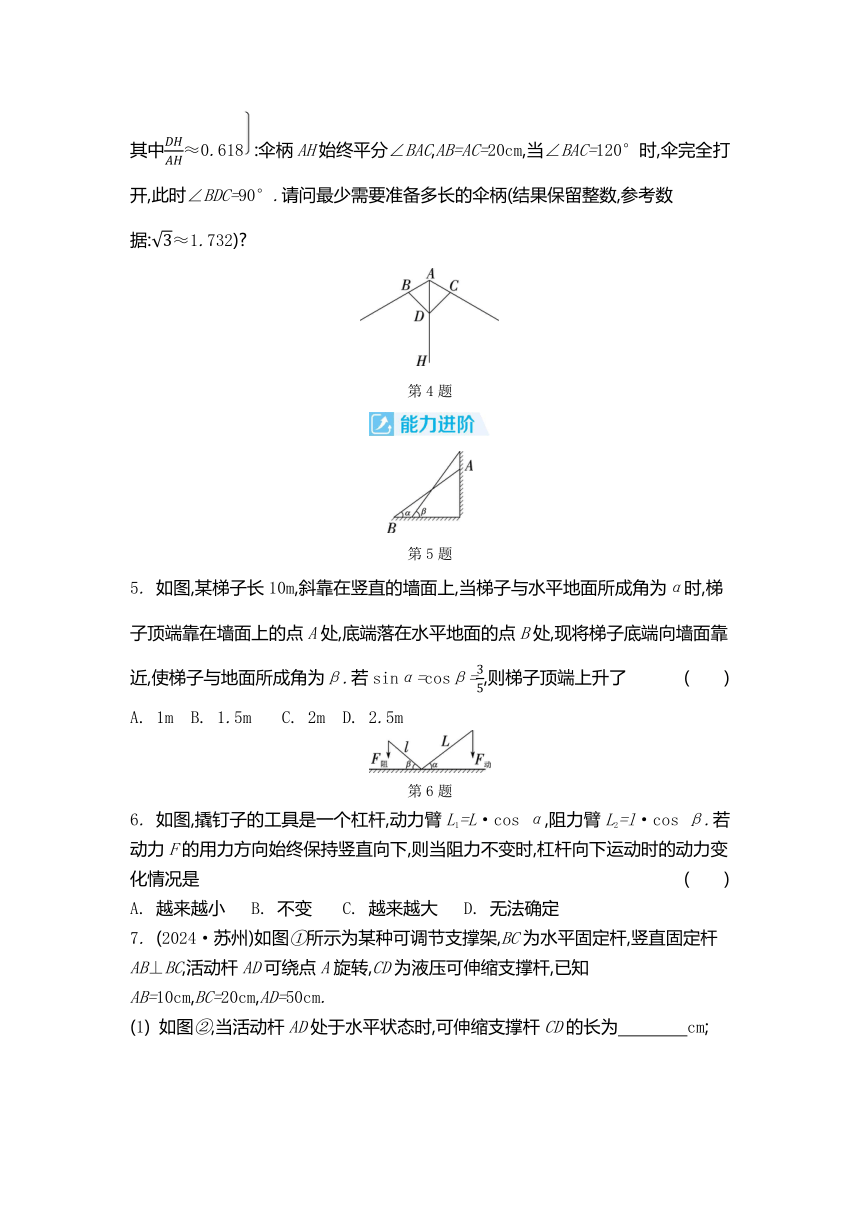
4. 湘潭县石鼓油纸伞因古老工艺和文化底蕴,已成为石鼓乡村旅游的一张靓丽名片.小文同学依据黄金分割的美学设计理念,设计了截面如图所示的伞骨结构其中≈0.618:伞柄AH始终平分∠BAC,AB=AC=20cm,当∠BAC=120°时,伞完全打开,此时∠BDC=90°.请问最少需要准备多长的伞柄(结果保留整数,参考数据:≈1.732)
第4题
第5题
5. 如图,某梯子长10m,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β.若sinα=cosβ=,则梯子顶端上升了 ( )
A. 1m B. 1.5m C. 2m D. 2.5m
第6题
6. 如图,撬钉子的工具是一个杠杆,动力臂L1=L·cos α,阻力臂L2=l·cos β.若动力F的用力方向始终保持竖直向下,则当阻力不变时,杠杆向下运动时的动力变化情况是 ( )
A. 越来越小 B. 不变 C. 越来越大 D. 无法确定
7. (2024·苏州)如图①所示为某种可调节支撑架,BC为水平固定杆,竖直固定杆AB⊥BC,活动杆AD可绕点A旋转,CD为液压可伸缩支撑杆,已知AB=10cm,BC=20cm,AD=50cm.
(1) 如图②,当活动杆AD处于水平状态时,可伸缩支撑杆CD的长为 cm;
(2) 如图③,当活动杆AD绕点A由水平状态按逆时针方向旋转角度α,且tanα=(α为锐角),则此时可伸缩支撑杆CD的长为 cm.
8. (2023·湘潭改编)如图所示为我国古代利用水力驱动的灌溉工具“筒车”的平面示意图.半径为3m的筒车☉O按逆时针方向每分钟转圈,筒车与水面分别交于点A、B,筒车的轴心O距离水面的高度OC为2.2m,筒车上均匀分布着若干个盛水筒,以某个盛水筒P刚浮出水面时开始计算时间.
(1) 经过 s,盛水筒P首次到达最高点.
(2) 浮出水面3.4s时,盛水筒P距离水面多高
(3) 若接水槽MN所在直线是☉O的切线,且与直线AB交于点M,MO=8m,则盛水筒P从最高点开始,至少经过多长时间恰好在直线MN上
第8题
第3课时 与仰角、俯角和方向角有关的问题
1. 如图,一渔船在海岛A南偏东20°方向的点B处遇险,测得海岛A与点B之间的距离为20海里,渔船将险情报告给位于海岛A的救援船后,沿北偏西80°方向向海岛C靠近,同时,从海岛A出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为 ( )
A. 10海里/时 B. 30海里/时 C. 20海里/时 D. 30海里/时
2. (2024·湖北)如图,某数学兴趣小组在校园内开展综合与实践活动,记录如下:① 选取与树底B位于同一水平地面的点D处,测量D、B两点间的距离为10m;② 站在点D处,用测角仪测量从眼睛C处看树顶A的仰角∠ACF=32.5°;③ 测量眼睛C处到地面的高度CD为1.6m.假设AB、CD均与地面垂直,则树AB的高度约为 m(参考数据:tan32.5°≈0.64).
3. (2024·绥化)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50m,则这栋楼的高度为 m.
4. (2024·兴安盟)综合实践活动中,数学兴趣小组利用无人机测量大楼的高度.如图,无人机在离地面40m的点D处,测得操控者A的俯角为30°,测得大楼BC楼顶C的俯角为45°,又经过人工测量得到操控者A和大楼BC之间的水平距离是80m,则大楼BC的高度是多少米(点A、B、C、D都在同一平面内,参考数据:≈1.7)
第4题
5. 一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏西42°方向上,在海岛B的北偏西84°方向上,则海岛B到灯塔C的距离为 ( )
A. 15海里 B. 20海里 C. 30海里 D. 60海里
6. (2024·雅安)在数学课外实践活动中,某小组测量一栋楼房CD的高度(如图),他们在点A处仰望楼顶,测得仰角为30°,再往楼房的方向前进50m至点B处,测得仰角为60°,那么这栋楼房的高度为(人的身高忽略不计) ( )
A. 25m B. 25m C. 25m D. 50m
7. (2024·赤峰)综合实践课上,航模小组用无人机测量古树AB的高度.如图,点C处与古树底部A处在同一水平面上,且AC=10m,无人机从点C处竖直上升到达点D处,测得古树顶部B的俯角为45°,古树底部A的俯角为65°,则古树AB的高度约为 m(精确到0.1m,参考数据:sin65°≈0.906,cos65°≈0.423,tan65°≈2.145).
8. (2023·营口)为了丰富学生的文化生活,学校利用假期组织学生到A地和B地参观学习.如图,学生从学校出发,走到C地时,发现A地位于C地的北偏西25°方向上,B地位于C地的北偏西55°方向上,老师将学生分成甲、乙两组,甲组前往A地,乙组前往B地,已知B地在A地的南偏西20°方向上,且相距1000米,请求出甲组学生比乙组学生大约多走多远的路程(参考数据:≈1.41,≈2.45).
第8题
9. (2024·巴中)某兴趣小组开展了测量电线塔高度的实践活动.如图,斜坡BE的坡度i=1∶,BE=6m,在点B处测得电线塔CD顶部D的仰角为45°,在点E处测得电线塔CD顶部D的仰角为60°.求:
(1) 点B离水平地面的高度AB;
(2) 电线塔CD的高度(结果保留根号).
第9题
7.6 用锐角三角函数解决问题
第1课时 与坡度和坡角有关的问题
1. B 2. A 3. 10 4. 10
5. 过点D作DE⊥BC,垂足为E.根据题意,得AF⊥BC,DE=AF.∵ 斜面AB的坡度i=3∶4,∴ =.∴ 设AF=3xm,则BF=4xm.∴ 在Rt△ABF中,AB==5xm.∵ 在Rt△DEC中,∠C=18°,CD=20m,∴ DE=CD·sin18°≈20×0.31=6.2(m).由AF=DE,得3x=6.2,解得x=.∴ AB=5×≈10.3(m).∴ 斜坡AB的长约为10.3m
6. B 7. 4
8. (1) 由题意,得在Rt△EFG中,∠G=90°,∴ tan∠EFG=i=1∶0.75==.设EG=4xm(x>0),则FG=3xm.∴ EF==5xm.∵ EF=15m,∴ 5x=15,解得x=3.∴ FG=3×3=9(m).∴ 山坡EF的水平宽度FG为9m (2) 设CF=ym.∴ L=CF+FG+EA=y+9+4=(y+13)m.又∵ H=AB+EG=22.5+4×3=34.5(m),H1=0.9m,∴ 日照间距系数=L∶(H-H1)==.∵ 该楼房的日照间距系数不低于1.25,∴ ≥1.25,即y≥29.∴ 要使该楼房的日照间距系数不低于1.25,底部C距F处至少29m远
9. (1) ∵ i=1∶2=AC∶BC,AC=4m,∴ BC=8m.∴ 水平宽度BC为8m (2) 延长DG交BC于点M,过点D作DN⊥BC,交BC于点N,交AB于点H.由题意,得DM⊥AB,∠ACB=90°,∴ ∠MGB=∠ACB=90°.∵ 在Rt△ABC中,tan∠ABC==,∴ 在Rt△GMB中,tan∠ABC==.∵ BG=3.5+2.5=6(m),∴ GM=3m.由题意,得DG=EF=2m,∴ DM=DG+GM=5m.∵ DN⊥BC,∴ ∠DNB=90°.∴ ∠ABC+∠NHB=90°.∵ ∠MGB=90°,∴ ∠GDH+∠GHD=90°.又∵ ∠GHD=∠NHB,∴ ∠GDH=∠ABC.∴ tan∠GDH=tan∠ABC==.设MN=xm,则DN=2xm.在Rt△DMN中,x2+(2x)2=52,解得x=(负值舍去).∴ DN≈4.5m.∴ 点D到地面的高约为4.5m
第2课时 与旋转等有关的问题
1. A 2. D 3. 8.2
4. 过点B作BE⊥AH于点E.∵ ∠BAC=120°,AH平分∠BAC,∴ ∠BAE=∠CAD=60°.∴ 在Rt△AEB中,AE=AB·cos60°=20×=10(cm),BE=AB·sin60°=20×=10(cm).∵ AB=AC,∠BAD=∠CAD,AD=AD,∴ △ABD≌△ACD.∴ ∠ADB=∠ADC=∠BDC=45°.∴ 在Rt△BED中,DE==10cm.∴ AD=AE+DE=10+10≈27.32(cm).∵ ≈0.618,设AH=xcm,∴ ≈0.618.∴ x≈72.∴ 最少需要准备72cm长的伞柄
5. C 6. A
7. (1) 10 解析:过点C作CE⊥AD,垂足为E.由题意,得AB=CE=10cm,BC=AE=20cm,∵ AD=50cm,∴ ED=AD-AE=50-20=30(cm).∴ 在Rt△CED中,由勾股定理,得CD===10(cm).∴ 可伸缩支撑杆CD的长为10cm.
(2) 20 解析:如图,过点D作DF⊥BC,交BC的延长线于点F,交AD'于点G.由题意,得AB=FG=10cm,AG=BF,∠AGD=90°.∵ 在Rt△ADG中,tanα==,∴ 设DG=3xcm,则AG=4xcm.∴ 在Rt△AGD中,由勾股定理,得AD==5xcm.∵ AD=50cm,∴ 5x=50,解得x=10.∴ AG=40cm,DG=30cm.∴ DF=DG+FG=30+10=40(cm),BF=AG=40cm.∵ BC=20cm,∴ CF=BF-BC=40-20=20(cm).∴ 在Rt△CFD中,由勾股定理,得CD===20(cm).∴ 此时可伸缩支撑杆CD的长为20cm.
8. (1) 27.4 解析:如图①,连接OA.由题意,得筒车每秒旋转360°×÷60=5°.∵ 在Rt△ACO中,cos ∠AOC===.∴ ∠AOC≈43°.∴ 盛水筒P首次到达最高点所需时间为=27.4(s).
(2) 如图①,连接OP,过点P作PD⊥OC于点D,盛水筒P浮出水面3.4 s时,∠AOP=3.4×5°=17°,∴ ∠POC=∠AOC+∠AOP=43°+17°=60°.在Rt△POD中,OD=OP·cos 60°=3×=1.5(m),∴ 浮出水面3.4 s时,盛水筒P距离水面2.2-1.5=0.7(m) (3) 如图②,延长CO交☉O于点H.∵ 点P在☉O上,且MN与☉O相切,∴ 当点P在直线MN上时,P是切点.延长MN与☉O交于点P,连接OP,则OP⊥MN.∵ 在Rt△OPM中,cos ∠POM==,∴ ∠POM≈68°.∵ 在Rt△COM中,cos ∠COM===,∴ ∠COM≈74°.∴ ∠POH=180°-∠POM-∠COM=180°-68°-74°=38°.∴ 需要的时间为=7.6(s).∴ 盛水筒P从最高点开始,至少经过7.6 s恰好在直线MN上
第3课时 与仰角、俯角和方向角有关的问题
1. D 2. 8 3. (50+50)
4. 如图,过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,则四边形BCFE是矩形.由题意,得AB=80m,DE=40m,∠ADE=90°-30°=60°,∠CDF=90°-45°=45°.∵ 在Rt△ADE中,tan∠ADE==tan60°=,∴ AE=DE=40m.∴ BE=AB-AE=(80-40)m.∵ 四边形BCFE是矩形,∴ BC=EF,CF=BE=(80-40)m.∵ 在Rt△DCF中,∠DFC=90°,∠CDF=∠DCF=45°,∴ DF=CF=(80-40)m.∴ BC=EF=DE-DF=40-80+40≈28(m).∴ 大楼BC的高度约是28m
5. C 6. A 7. 11.5
8. 如图,过点B作BE⊥AC,垂足为E.由题意,得∠ACD=25°,∠BCD=55°,∠FAB=20°,AB=1000米,CD∥FA,∴ ∠CAF=∠ACD=25°.∴ ∠BAC=∠FAB+∠CAF=45°,∠ACB=∠BCD-∠ACD=30°.∴ 在Rt△ABE中,AE=AB·cos45°=1000×=500(米),BE=AB·sin45°=1000×=500(米).∴ 在Rt△BCE中,BC==1000米,CE==500÷=500(米).∴ AC=AE+CE=(500+500)米.∴ AC-BC=500+500-1000=500-500≈520(米).∴ 甲组学生比乙组学生大约多走520米的路程
9. (1) 由题意,得BA⊥AE.∵ 斜坡BE的坡度i=1∶,∴ 在Rt△ABE中,tan∠BEA===.∴ ∠BEA=30°.∵ BE=6m,∴ 易得AB=BE=3m.∴ 点B离水平地面的高度AB为3m (2) 如图,过点B作BF⊥CD,垂足为F,则四边形BACF为矩形.∴ AB=CF=3m,BF=AC.设EC=xm.∵ 在Rt△ABE中,AE=BE·cos30°=3m,∴ BF=AC=AE+CE=(x+3)m.∵ 在Rt△CDE中,∠DEC=60°,∴ CD=CE·tan60°=xm.∵ 在Rt△BDF中,∠DBF=45°,∴ DF=BF·tan45°=(x+3)m.∵ DF+CF=CD,∴ x+3+3=x,解得x=6+3.∴ CD=(6+9)m.∴ 电线塔CD的高度为(6+9)m
第1课时 与坡度和坡角有关的问题
1.
(2024·威海改编)如图,某商场有一自动扶梯,其坡角为28°,高为7米.用计算器求AB的长,下列按键顺序正确的是 ( )
A. 7 × sin 2 8 = B. 7 ÷ sin 2 8 =
C. 7 × tan 2 8 = D. 7 ÷ tan 2 8 =
2. 已知某河堤的横截面为梯形ABCD,上底长为4m,堤高为6m,斜坡AD的坡度为1∶3,斜坡CB的坡角为45°,则河堤横截面的下底长为 ( )
A. 28m B. 12m C. 60m D. 24m
3. 一条上山直道的坡度为1∶7,沿这条直道上山,每前进100m所上升的高度为 m.
4. 如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB的长为26m,斜坡AB的坡比为12∶5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.若改造时保持坡脚A不动,则坡顶B沿BC至少向右移 m,才能确保山体不滑坡(参考数据:tan 50°≈1.2).
5. (2023·仙桃)为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形ABCD,斜面坡度i=3∶4是指坡面的铅直高度AF与水平宽度BF的比.已知斜坡CD的长为20m,∠C=18°,求斜坡AB的长(精确到0.1m,参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32).
第5题
第6题
6. 如图,小明去爬山,在山脚看山顶的角度为30°,小明在坡比为5∶12的山坡上走1300m,此时小明看山顶的角度为60°,山高为 ( )
A. (600-250)m B. (600-250)m
C. (350+350)m D. 500m
第7题
7. (2024·眉山改编)如图,坡面CD的坡度为1∶,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线的夹角成60°时,测得小树在坡顶平地上的树影BC=3m,在斜坡上的树影CD=m,则小树AB的高是 m.
8. 日照间距系数反映了房屋日照情况.如图①,当前、后房屋都朝向正南时,日照间距系数=L∶(H-H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面的高度.如图②,山坡EF朝北,EF的长为15m,坡度i=1∶0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到点E的距离为4m.
(1) 求山坡EF的水平宽度FG;
(2) 欲在楼房AB正北侧山脚的平地FN上建一楼房CD,该楼房底层窗台P处至地面C处的高度为0.9m,要使该楼房的日照间距系数不低于1.25,底部C距F处至少多远
第8题
9. 如图,某仓储中心有一斜坡AB,其坡度为i=1∶2,顶部A处的高AC为4m,点B、C在同一水平地面上.
(1) 求斜坡AB的水平宽度BC.
(2) 矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m.将该货柜沿斜坡向上运送,当BF=3.5m时,求点D到地面的高(精确到0.1m,参考数据:≈2.236).
第9题
第2课时 与旋转等有关的问题
1. 某停车场入口栏杆如图所示,栏杆从水平位置AB绕点O旋转到CD的位置,AO=a.若栏杆的旋转角为∠AOD=41°,则栏杆端点A上升的垂直距离为 ( )
A. asin41° B. acos41° C. D. atan41°
2. 如图所示为一个小孩荡秋千的示意图,秋千链子OA的长度为2m,当秋千向两边摆动时,两边摆动的角度均为30°,则秋千摆动至最高位置与最低位置时的高度差为 ( )
A. m B. m C. (2-)m D. (2-)m
3. (2024·兰州)单摆是一种能够产生往复摆动的装置.如图,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,BD⊥OA,∠BOA=64°,BD=20.5cm;当摆球摆动至点C时,∠COA=37°,CE⊥OA.由此可得ED的长约为 cm(精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05).
4. 湘潭县石鼓油纸伞因古老工艺和文化底蕴,已成为石鼓乡村旅游的一张靓丽名片.小文同学依据黄金分割的美学设计理念,设计了截面如图所示的伞骨结构其中≈0.618:伞柄AH始终平分∠BAC,AB=AC=20cm,当∠BAC=120°时,伞完全打开,此时∠BDC=90°.请问最少需要准备多长的伞柄(结果保留整数,参考数据:≈1.732)
第4题
第5题
5. 如图,某梯子长10m,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β.若sinα=cosβ=,则梯子顶端上升了 ( )
A. 1m B. 1.5m C. 2m D. 2.5m
第6题
6. 如图,撬钉子的工具是一个杠杆,动力臂L1=L·cos α,阻力臂L2=l·cos β.若动力F的用力方向始终保持竖直向下,则当阻力不变时,杠杆向下运动时的动力变化情况是 ( )
A. 越来越小 B. 不变 C. 越来越大 D. 无法确定
7. (2024·苏州)如图①所示为某种可调节支撑架,BC为水平固定杆,竖直固定杆AB⊥BC,活动杆AD可绕点A旋转,CD为液压可伸缩支撑杆,已知AB=10cm,BC=20cm,AD=50cm.
(1) 如图②,当活动杆AD处于水平状态时,可伸缩支撑杆CD的长为 cm;
(2) 如图③,当活动杆AD绕点A由水平状态按逆时针方向旋转角度α,且tanα=(α为锐角),则此时可伸缩支撑杆CD的长为 cm.
8. (2023·湘潭改编)如图所示为我国古代利用水力驱动的灌溉工具“筒车”的平面示意图.半径为3m的筒车☉O按逆时针方向每分钟转圈,筒车与水面分别交于点A、B,筒车的轴心O距离水面的高度OC为2.2m,筒车上均匀分布着若干个盛水筒,以某个盛水筒P刚浮出水面时开始计算时间.
(1) 经过 s,盛水筒P首次到达最高点.
(2) 浮出水面3.4s时,盛水筒P距离水面多高
(3) 若接水槽MN所在直线是☉O的切线,且与直线AB交于点M,MO=8m,则盛水筒P从最高点开始,至少经过多长时间恰好在直线MN上
第8题
第3课时 与仰角、俯角和方向角有关的问题
1. 如图,一渔船在海岛A南偏东20°方向的点B处遇险,测得海岛A与点B之间的距离为20海里,渔船将险情报告给位于海岛A的救援船后,沿北偏西80°方向向海岛C靠近,同时,从海岛A出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为 ( )
A. 10海里/时 B. 30海里/时 C. 20海里/时 D. 30海里/时
2. (2024·湖北)如图,某数学兴趣小组在校园内开展综合与实践活动,记录如下:① 选取与树底B位于同一水平地面的点D处,测量D、B两点间的距离为10m;② 站在点D处,用测角仪测量从眼睛C处看树顶A的仰角∠ACF=32.5°;③ 测量眼睛C处到地面的高度CD为1.6m.假设AB、CD均与地面垂直,则树AB的高度约为 m(参考数据:tan32.5°≈0.64).
3. (2024·绥化)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50m,则这栋楼的高度为 m.
4. (2024·兴安盟)综合实践活动中,数学兴趣小组利用无人机测量大楼的高度.如图,无人机在离地面40m的点D处,测得操控者A的俯角为30°,测得大楼BC楼顶C的俯角为45°,又经过人工测量得到操控者A和大楼BC之间的水平距离是80m,则大楼BC的高度是多少米(点A、B、C、D都在同一平面内,参考数据:≈1.7)
第4题
5. 一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏西42°方向上,在海岛B的北偏西84°方向上,则海岛B到灯塔C的距离为 ( )
A. 15海里 B. 20海里 C. 30海里 D. 60海里
6. (2024·雅安)在数学课外实践活动中,某小组测量一栋楼房CD的高度(如图),他们在点A处仰望楼顶,测得仰角为30°,再往楼房的方向前进50m至点B处,测得仰角为60°,那么这栋楼房的高度为(人的身高忽略不计) ( )
A. 25m B. 25m C. 25m D. 50m
7. (2024·赤峰)综合实践课上,航模小组用无人机测量古树AB的高度.如图,点C处与古树底部A处在同一水平面上,且AC=10m,无人机从点C处竖直上升到达点D处,测得古树顶部B的俯角为45°,古树底部A的俯角为65°,则古树AB的高度约为 m(精确到0.1m,参考数据:sin65°≈0.906,cos65°≈0.423,tan65°≈2.145).
8. (2023·营口)为了丰富学生的文化生活,学校利用假期组织学生到A地和B地参观学习.如图,学生从学校出发,走到C地时,发现A地位于C地的北偏西25°方向上,B地位于C地的北偏西55°方向上,老师将学生分成甲、乙两组,甲组前往A地,乙组前往B地,已知B地在A地的南偏西20°方向上,且相距1000米,请求出甲组学生比乙组学生大约多走多远的路程(参考数据:≈1.41,≈2.45).
第8题
9. (2024·巴中)某兴趣小组开展了测量电线塔高度的实践活动.如图,斜坡BE的坡度i=1∶,BE=6m,在点B处测得电线塔CD顶部D的仰角为45°,在点E处测得电线塔CD顶部D的仰角为60°.求:
(1) 点B离水平地面的高度AB;
(2) 电线塔CD的高度(结果保留根号).
第9题
7.6 用锐角三角函数解决问题
第1课时 与坡度和坡角有关的问题
1. B 2. A 3. 10 4. 10
5. 过点D作DE⊥BC,垂足为E.根据题意,得AF⊥BC,DE=AF.∵ 斜面AB的坡度i=3∶4,∴ =.∴ 设AF=3xm,则BF=4xm.∴ 在Rt△ABF中,AB==5xm.∵ 在Rt△DEC中,∠C=18°,CD=20m,∴ DE=CD·sin18°≈20×0.31=6.2(m).由AF=DE,得3x=6.2,解得x=.∴ AB=5×≈10.3(m).∴ 斜坡AB的长约为10.3m
6. B 7. 4
8. (1) 由题意,得在Rt△EFG中,∠G=90°,∴ tan∠EFG=i=1∶0.75==.设EG=4xm(x>0),则FG=3xm.∴ EF==5xm.∵ EF=15m,∴ 5x=15,解得x=3.∴ FG=3×3=9(m).∴ 山坡EF的水平宽度FG为9m (2) 设CF=ym.∴ L=CF+FG+EA=y+9+4=(y+13)m.又∵ H=AB+EG=22.5+4×3=34.5(m),H1=0.9m,∴ 日照间距系数=L∶(H-H1)==.∵ 该楼房的日照间距系数不低于1.25,∴ ≥1.25,即y≥29.∴ 要使该楼房的日照间距系数不低于1.25,底部C距F处至少29m远
9. (1) ∵ i=1∶2=AC∶BC,AC=4m,∴ BC=8m.∴ 水平宽度BC为8m (2) 延长DG交BC于点M,过点D作DN⊥BC,交BC于点N,交AB于点H.由题意,得DM⊥AB,∠ACB=90°,∴ ∠MGB=∠ACB=90°.∵ 在Rt△ABC中,tan∠ABC==,∴ 在Rt△GMB中,tan∠ABC==.∵ BG=3.5+2.5=6(m),∴ GM=3m.由题意,得DG=EF=2m,∴ DM=DG+GM=5m.∵ DN⊥BC,∴ ∠DNB=90°.∴ ∠ABC+∠NHB=90°.∵ ∠MGB=90°,∴ ∠GDH+∠GHD=90°.又∵ ∠GHD=∠NHB,∴ ∠GDH=∠ABC.∴ tan∠GDH=tan∠ABC==.设MN=xm,则DN=2xm.在Rt△DMN中,x2+(2x)2=52,解得x=(负值舍去).∴ DN≈4.5m.∴ 点D到地面的高约为4.5m
第2课时 与旋转等有关的问题
1. A 2. D 3. 8.2
4. 过点B作BE⊥AH于点E.∵ ∠BAC=120°,AH平分∠BAC,∴ ∠BAE=∠CAD=60°.∴ 在Rt△AEB中,AE=AB·cos60°=20×=10(cm),BE=AB·sin60°=20×=10(cm).∵ AB=AC,∠BAD=∠CAD,AD=AD,∴ △ABD≌△ACD.∴ ∠ADB=∠ADC=∠BDC=45°.∴ 在Rt△BED中,DE==10cm.∴ AD=AE+DE=10+10≈27.32(cm).∵ ≈0.618,设AH=xcm,∴ ≈0.618.∴ x≈72.∴ 最少需要准备72cm长的伞柄
5. C 6. A
7. (1) 10 解析:过点C作CE⊥AD,垂足为E.由题意,得AB=CE=10cm,BC=AE=20cm,∵ AD=50cm,∴ ED=AD-AE=50-20=30(cm).∴ 在Rt△CED中,由勾股定理,得CD===10(cm).∴ 可伸缩支撑杆CD的长为10cm.
(2) 20 解析:如图,过点D作DF⊥BC,交BC的延长线于点F,交AD'于点G.由题意,得AB=FG=10cm,AG=BF,∠AGD=90°.∵ 在Rt△ADG中,tanα==,∴ 设DG=3xcm,则AG=4xcm.∴ 在Rt△AGD中,由勾股定理,得AD==5xcm.∵ AD=50cm,∴ 5x=50,解得x=10.∴ AG=40cm,DG=30cm.∴ DF=DG+FG=30+10=40(cm),BF=AG=40cm.∵ BC=20cm,∴ CF=BF-BC=40-20=20(cm).∴ 在Rt△CFD中,由勾股定理,得CD===20(cm).∴ 此时可伸缩支撑杆CD的长为20cm.
8. (1) 27.4 解析:如图①,连接OA.由题意,得筒车每秒旋转360°×÷60=5°.∵ 在Rt△ACO中,cos ∠AOC===.∴ ∠AOC≈43°.∴ 盛水筒P首次到达最高点所需时间为=27.4(s).
(2) 如图①,连接OP,过点P作PD⊥OC于点D,盛水筒P浮出水面3.4 s时,∠AOP=3.4×5°=17°,∴ ∠POC=∠AOC+∠AOP=43°+17°=60°.在Rt△POD中,OD=OP·cos 60°=3×=1.5(m),∴ 浮出水面3.4 s时,盛水筒P距离水面2.2-1.5=0.7(m) (3) 如图②,延长CO交☉O于点H.∵ 点P在☉O上,且MN与☉O相切,∴ 当点P在直线MN上时,P是切点.延长MN与☉O交于点P,连接OP,则OP⊥MN.∵ 在Rt△OPM中,cos ∠POM==,∴ ∠POM≈68°.∵ 在Rt△COM中,cos ∠COM===,∴ ∠COM≈74°.∴ ∠POH=180°-∠POM-∠COM=180°-68°-74°=38°.∴ 需要的时间为=7.6(s).∴ 盛水筒P从最高点开始,至少经过7.6 s恰好在直线MN上
第3课时 与仰角、俯角和方向角有关的问题
1. D 2. 8 3. (50+50)
4. 如图,过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,则四边形BCFE是矩形.由题意,得AB=80m,DE=40m,∠ADE=90°-30°=60°,∠CDF=90°-45°=45°.∵ 在Rt△ADE中,tan∠ADE==tan60°=,∴ AE=DE=40m.∴ BE=AB-AE=(80-40)m.∵ 四边形BCFE是矩形,∴ BC=EF,CF=BE=(80-40)m.∵ 在Rt△DCF中,∠DFC=90°,∠CDF=∠DCF=45°,∴ DF=CF=(80-40)m.∴ BC=EF=DE-DF=40-80+40≈28(m).∴ 大楼BC的高度约是28m
5. C 6. A 7. 11.5
8. 如图,过点B作BE⊥AC,垂足为E.由题意,得∠ACD=25°,∠BCD=55°,∠FAB=20°,AB=1000米,CD∥FA,∴ ∠CAF=∠ACD=25°.∴ ∠BAC=∠FAB+∠CAF=45°,∠ACB=∠BCD-∠ACD=30°.∴ 在Rt△ABE中,AE=AB·cos45°=1000×=500(米),BE=AB·sin45°=1000×=500(米).∴ 在Rt△BCE中,BC==1000米,CE==500÷=500(米).∴ AC=AE+CE=(500+500)米.∴ AC-BC=500+500-1000=500-500≈520(米).∴ 甲组学生比乙组学生大约多走520米的路程
9. (1) 由题意,得BA⊥AE.∵ 斜坡BE的坡度i=1∶,∴ 在Rt△ABE中,tan∠BEA===.∴ ∠BEA=30°.∵ BE=6m,∴ 易得AB=BE=3m.∴ 点B离水平地面的高度AB为3m (2) 如图,过点B作BF⊥CD,垂足为F,则四边形BACF为矩形.∴ AB=CF=3m,BF=AC.设EC=xm.∵ 在Rt△ABE中,AE=BE·cos30°=3m,∴ BF=AC=AE+CE=(x+3)m.∵ 在Rt△CDE中,∠DEC=60°,∴ CD=CE·tan60°=xm.∵ 在Rt△BDF中,∠DBF=45°,∴ DF=BF·tan45°=(x+3)m.∵ DF+CF=CD,∴ x+3+3=x,解得x=6+3.∴ CD=(6+9)m.∴ 电线塔CD的高度为(6+9)m
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
