第6章图形的相似 整合提升(含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 第6章图形的相似 整合提升(含答案) 2024-2025学年数学苏科版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 158.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览


文档简介
第6章图形的相似 整合提升
考点一 成比例线段与黄金分割
1. 已知四条线段的长度分别为m、n、p、q(m、n、p、q均不为0),其长度满足等式mn=pq,将它改写成比例式的形式,错误的是 ( )
A. = B. = C. = D. =
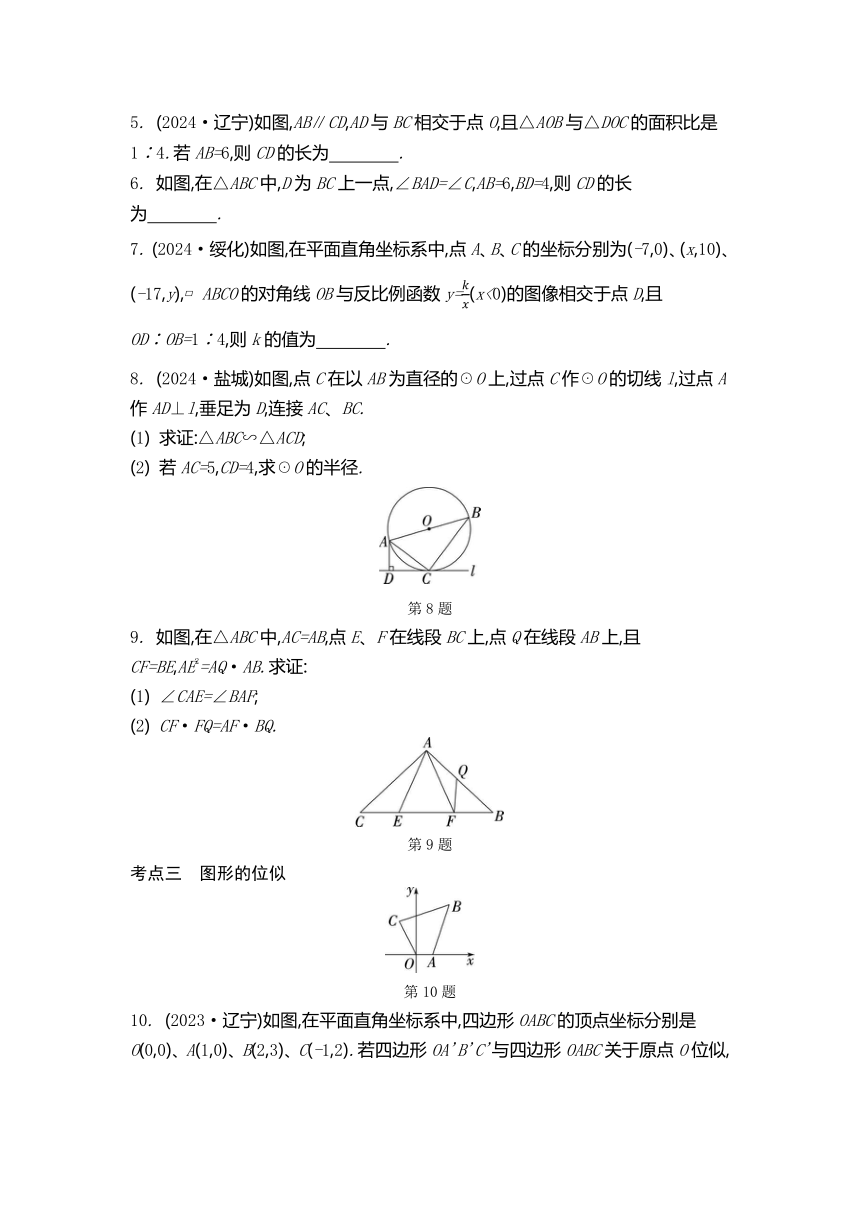
2. 融融陪同父母选购家装木地板,她感觉某品牌木地板拼接图(实物如图①)比较美观,通过手绘(如图②)、测量、计算发现,E是AD的黄金分割点,即DE≈0.618AD.延长HF与AD相交于点G,则EG≈ DE(精确到0.001).
考点二 相似三角形的判定与性质
3. △ABC的三边长分别为2、3、4,另有一个与它相似的三角形DEF,其最长边的长为12,则△DEF的周长是 ( )
A. 54 B. 36 C. 27 D. 21
4. 如图,F是线段CD上除端点外的一点,将△ADF绕正方形ABCD的顶点A按顺时针方向旋转90°,得到△ABE,连接EF,交AB于点H.下列结论正确的是 ( )
A. ∠EAF=120° B. AE∶EF=1∶
C. AF2=EH·EF D. EB∶AD=EH∶HF
5. (2024·辽宁)如图,AB∥CD,AD与BC相交于点O,且△AOB与△DOC的面积比是1∶4.若AB=6,则CD的长为 .
6. 如图,在△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为 .
7. (2024·绥化)如图,在平面直角坐标系中,点A、B、C的坐标分别为(-7,0)、(x,10)、(-17,y), ABCO的对角线OB与反比例函数y=(x<0)的图像相交于点D,且OD∶OB=1∶4,则k的值为 .
8. (2024·盐城)如图,点C在以AB为直径的☉O上,过点C作☉O的切线l,过点A作AD⊥l,垂足为D,连接AC、BC.
(1) 求证:△ABC∽△ACD;
(2) 若AC=5,CD=4,求☉O的半径.
第8题
9. 如图,在△ABC中,AC=AB,点E、F在线段BC上,点Q在线段AB上,且CF=BE,AE2=AQ·AB.求证:
(1) ∠CAE=∠BAF;
(2) CF·FQ=AF·BQ.
第9题
考点三 图形的位似
第10题
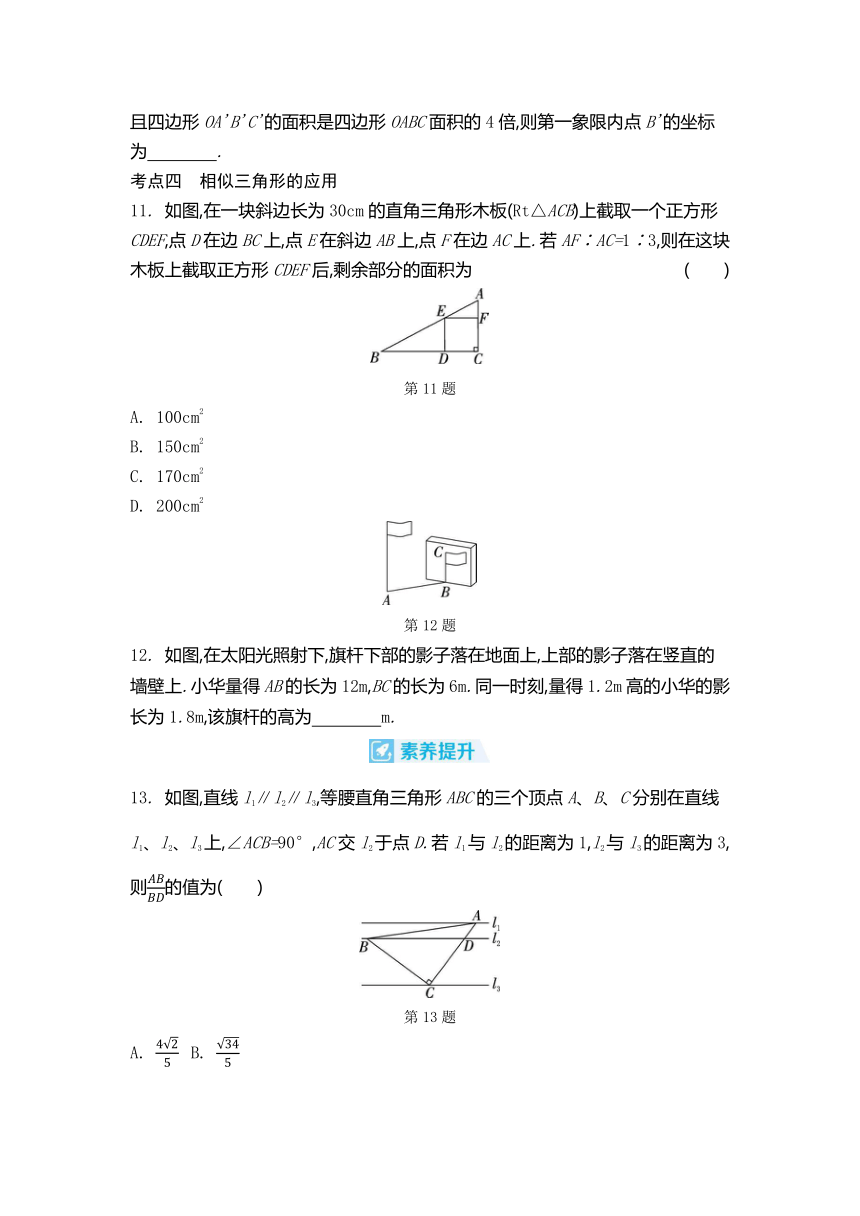
10. (2023·辽宁)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0)、A(1,0)、B(2,3)、C(-1,2).若四边形OA'B'C'与四边形OABC关于原点O位似,且四边形OA'B'C'的面积是四边形OABC面积的4倍,则第一象限内点B'的坐标为 .
考点四 相似三角形的应用
11. 如图,在一块斜边长为30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上.若AF∶AC=1∶3,则在这块木板上截取正方形CDEF后,剩余部分的面积为 ( )
第11题
A. 100cm2
B. 150cm2
C. 170cm2
D. 200cm2
第12题
12. 如图,在太阳光照射下,旗杆下部的影子落在地面上,上部的影子落在竖直的墙壁上.小华量得AB的长为12m,BC的长为6m.同一时刻,量得1.2m高的小华的影长为1.8m,该旗杆的高为 m.
13. 如图,直线l1∥l2∥l3,等腰直角三角形ABC的三个顶点A、B、C分别在直线l1、l2、l3上,∠ACB=90°,AC交l2于点D.若l1与l2的距离为1,l2与l3的距离为3,则的值为( )
第13题
A. B.
C. D.
14. (2024·南通)在△ABC中,∠B=∠C=α(0°<α<45°),AH⊥BC,垂足为H,D是线段HC上的动点(不与点H、C重合),将线段DH绕点D按顺时针方向旋转2α得到线段DE.两名同学经过深入研究,小明发现:当点E落在边AC上时,D为HC的中点;小丽发现:连接AE,当AE的长最小时,AH2=AB·AE.下列说法中,正确的是 ( )
A. 小明正确,小丽错误 B. 小明错误,小丽正确
C. 小明、小丽都正确 D. 小明、小丽都错误
15. (2024·无锡)如图,在△ABC中,AC=2,AB=3,直线CM∥AB,E是BC上的动点(端点除外),射线AE交CM于点D.在射线AE上取一点P,使得AP=2ED,过点P作PQ∥AB,交射线AC于点Q.设AQ=x,PQ=y.当x=y时,CD的长为 ;在点E的运动过程中,y关于x的函数表达式为 .
16. 如图,在平面直角坐标系中,点C、D的坐标分别为(2,3)、(1,0).现以原点O为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上,且OB=2,则点C的对应点A的坐标为 .
17. 已知两个直角三角形的三边长分别为3、4、m和6、8、n,且这两个直角三角形不相似,则m+n的值为 .
18. (2023·日照)如图,在矩形ABCD中,AB=6,AD=8,点P在对角线BD上,过点P作MN⊥BD,交边AD、BC于点M、N,过点M作ME⊥AD,交BD于点E,连接EN、BM、DN.有下列结论:① EM=EN;② 四边形MBND的面积不变;③ 当AM∶MD=1∶2时,S△MPE=;④ BM+MN+ND的最小值是20.其中,正确的是 (填序号).
19. (2023·云南)如图,BC是☉O的直径,A是☉O上异于点B、C的点.☉O外的点E在射线CB上,直线EA与CD垂直,垂足为D,连接AB、AC,且DA·AC=DC·AB.
(1) 求证:直线EA是☉O的切线;
(2) 若BC=BE,S△ACD=mS△BAE,求常数m的值.
第19题
20. 若一个三角形一条边的长的平方等于另外两条边的长的乘积,则我们把这个三角形叫做比例三角形.
(1) 已知△ABC是比例三角形,AB=2,BC=3,求出所有满足条件的AC的长.
(2) 如图①,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠CDA.求证:△ABC是比例三角形.
(3) 如图②,在(2)的条件下,当∠CDA=90°时,求的值.
第20题
第6章整合提升
1. D
2. 0.618 解析:∵ E是AD的黄金分割点,且DE≈0.618AD,∴ =≈0.618.根据题意,得EG=AE,∴ ≈0.618.∴ EG≈0.618DE.
3. C 4. D 5. 12 6. 5 7. -15
8. (1) 连接OC.∵ l是☉O的切线,∴ OC⊥l.∴ ∠OCD=90°.∵ AD⊥l,∴ ∠ADC=90°.∴ ∠OCD+∠ADC=180°.∴ OC∥AD.∴ ∠CAD=∠ACO.∵ OA=OC,∴ ∠BAC=∠ACO.∴ ∠CAD=∠BAC.∵ AB为☉O的直径,∴ ∠ACB=90°.∴ ∠ACB=∠ADC.∴ △ABC∽△ACD (2) ∵ 在Rt△ADC中,AC=5,CD=4,∴ AD==3.∵ △ABC∽△ACD,∴ =.∴ =.∴ AB=.∴ ☉O的半径为AB=
9. (1) ∵ AC=AB,∴ ∠C=∠B.∵ CF=BE,∴ CF-EF=BE-EF,即CE=BF.在△ACE和△ABF中,∴ △ACE≌△ABF.∴ ∠CAE=∠BAF (2) ∵ △ACE≌△ABF,∴ AE=AF,∠CAE=∠BAF. ∵ AE2=AQ·AB,AC=AB,∴ =.又∵ ∠CAE=∠FAQ,∴ △ACE∽△AFQ.∴ ∠AEC=∠AQF.∴ ∠AEF=∠BQF.∵ AE=AF,∴ ∠AEF=∠AFE.∴ ∠AFE=∠BQF.又∵ ∠C=∠B,∴ △CAF∽△BFQ.∴ =,即CF·FQ=AF·BQ
10. (4,6) 11. A 12. 14
13. A 解析:过点A作AE⊥l3于点E,交l2于点G.由l1∥l2∥l3,得==,即CD=3AD.设AD=a,则CD=3a,AC=CD+AD=4a.由题意,得BC=AC,∴ BC=4a.在Rt△BCD中,由勾股定理,得BD==5a.在Rt△ABC中,AB==4a.∴ =.
14. C
15. 2 y= 解析:证△APQ∽△ADC,得=,代入AC=2,x=y,可求CD=2.设DE=t,则AP=2t,证△APQ∽△ADC,得==.∴ CD=,AD=.证△CDE∽△BAE,得=,即=,整理,得y=.
16. (4,6)或(-4,-6)
17. 5+2或10+ 解析:当3、4为直角边长,6、8也为直角边长时,两个直角三角形相似,不合题意;当3、4为直角边长,易得m=5时,8为另一个直角三角形的斜边长,由勾股定理,得其另一直角边长为=2,此时m+n=5+2;当6、8为直角边长,易得n=10时,4为另一个直角三角形的斜边长,由勾股定理,得其另一直角边长为=,此时m+n=10+.综上所述,m+n的值为5+2或10+.
18. ②③④
19. (1) 连接OA.∵ DA·AC=DC·AB,∴ =.∵ BC是☉O的直径,∴ ∠BAC=90°.∵ EA⊥CD,∴ ∠ADC=90°.∴ ∠BAC=∠ADC.∴ △ABC∽△DAC.∴ ∠ACB=∠DCA.∵ OA=OC,∴ ∠OAC=∠ACB.∴ ∠OAC=∠DCA.∴ OA∥CD.∴ ∠OAE=∠ADC=90°.∴ OA⊥DE.又∵ OA为☉O的半径,∴ 直线EA是☉O的切线 (2) ∵ BC=BE,∴ S△BAE=S△ABC=S△ACE.∵ OB=OA,∴ ∠OBA=∠OAB.∵ ∠BAC=90°,∠OAE=90°,∴ ∠OBA +∠ACE=90°,∠OAB +∠BAE=90°.∴ ∠ACE=∠BAE.又∵ ∠E=∠E,∴ △ACE∽△BAE.∴ ==2.设BA2=x,则AC2=2x.∴ 在Rt△ABC中,BC2=AC2+BA2=3x.∴ ==.由(1),得△ABC∽△DAC,∴ ==,即=.∴ S△ACD=S△BAE.∴ m=
20. (1) 由题意,分三种情况讨论:① AC2=AB·BC,∴ AC=(负值舍去);② AB2=AC·BC,∴ AC=;③ BC2=AB·AC,∴ AC=.综上所述,AC的长为或或 (2) ∵ AD∥BC,∴ ∠ACB=∠DAC.又∵ ∠BAC=∠CDA,∴ △ABC∽△DCA.∴ =,即CA2=BC·AD.∵ AD∥BC,∴ ∠ADB=∠CBD.∵ BD平分∠ABC,∴ ∠ABD=∠CBD.∴ ∠ADB=∠ABD.∴ AD=AB.∴ CA2=BC·AB.∴ △ABC是比例三角形 (3) 过点A作AH⊥BD于点H.∵ AD=AB,AH⊥BD,∴ ∠BHA=90°,BH=BD.∵ AD∥BC,∠CDA=90°,∴ ∠BCD=180°-∠CDA=90°.∴ ∠BHA=∠BCD=90°.又∵ ∠ABH=∠DBC,∴ △ABH∽△DBC.∴ =,即AB·BC=BH·DB.∴ AB·BC=BD2.又∵ AB·BC=AC2,∴ BD2=AC2.∴ =
考点一 成比例线段与黄金分割
1. 已知四条线段的长度分别为m、n、p、q(m、n、p、q均不为0),其长度满足等式mn=pq,将它改写成比例式的形式,错误的是 ( )
A. = B. = C. = D. =
2. 融融陪同父母选购家装木地板,她感觉某品牌木地板拼接图(实物如图①)比较美观,通过手绘(如图②)、测量、计算发现,E是AD的黄金分割点,即DE≈0.618AD.延长HF与AD相交于点G,则EG≈ DE(精确到0.001).
考点二 相似三角形的判定与性质
3. △ABC的三边长分别为2、3、4,另有一个与它相似的三角形DEF,其最长边的长为12,则△DEF的周长是 ( )
A. 54 B. 36 C. 27 D. 21
4. 如图,F是线段CD上除端点外的一点,将△ADF绕正方形ABCD的顶点A按顺时针方向旋转90°,得到△ABE,连接EF,交AB于点H.下列结论正确的是 ( )
A. ∠EAF=120° B. AE∶EF=1∶
C. AF2=EH·EF D. EB∶AD=EH∶HF
5. (2024·辽宁)如图,AB∥CD,AD与BC相交于点O,且△AOB与△DOC的面积比是1∶4.若AB=6,则CD的长为 .
6. 如图,在△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为 .
7. (2024·绥化)如图,在平面直角坐标系中,点A、B、C的坐标分别为(-7,0)、(x,10)、(-17,y), ABCO的对角线OB与反比例函数y=(x<0)的图像相交于点D,且OD∶OB=1∶4,则k的值为 .
8. (2024·盐城)如图,点C在以AB为直径的☉O上,过点C作☉O的切线l,过点A作AD⊥l,垂足为D,连接AC、BC.
(1) 求证:△ABC∽△ACD;
(2) 若AC=5,CD=4,求☉O的半径.
第8题
9. 如图,在△ABC中,AC=AB,点E、F在线段BC上,点Q在线段AB上,且CF=BE,AE2=AQ·AB.求证:
(1) ∠CAE=∠BAF;
(2) CF·FQ=AF·BQ.
第9题
考点三 图形的位似
第10题
10. (2023·辽宁)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0)、A(1,0)、B(2,3)、C(-1,2).若四边形OA'B'C'与四边形OABC关于原点O位似,且四边形OA'B'C'的面积是四边形OABC面积的4倍,则第一象限内点B'的坐标为 .
考点四 相似三角形的应用
11. 如图,在一块斜边长为30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上.若AF∶AC=1∶3,则在这块木板上截取正方形CDEF后,剩余部分的面积为 ( )
第11题
A. 100cm2
B. 150cm2
C. 170cm2
D. 200cm2
第12题
12. 如图,在太阳光照射下,旗杆下部的影子落在地面上,上部的影子落在竖直的墙壁上.小华量得AB的长为12m,BC的长为6m.同一时刻,量得1.2m高的小华的影长为1.8m,该旗杆的高为 m.
13. 如图,直线l1∥l2∥l3,等腰直角三角形ABC的三个顶点A、B、C分别在直线l1、l2、l3上,∠ACB=90°,AC交l2于点D.若l1与l2的距离为1,l2与l3的距离为3,则的值为( )
第13题
A. B.
C. D.
14. (2024·南通)在△ABC中,∠B=∠C=α(0°<α<45°),AH⊥BC,垂足为H,D是线段HC上的动点(不与点H、C重合),将线段DH绕点D按顺时针方向旋转2α得到线段DE.两名同学经过深入研究,小明发现:当点E落在边AC上时,D为HC的中点;小丽发现:连接AE,当AE的长最小时,AH2=AB·AE.下列说法中,正确的是 ( )
A. 小明正确,小丽错误 B. 小明错误,小丽正确
C. 小明、小丽都正确 D. 小明、小丽都错误
15. (2024·无锡)如图,在△ABC中,AC=2,AB=3,直线CM∥AB,E是BC上的动点(端点除外),射线AE交CM于点D.在射线AE上取一点P,使得AP=2ED,过点P作PQ∥AB,交射线AC于点Q.设AQ=x,PQ=y.当x=y时,CD的长为 ;在点E的运动过程中,y关于x的函数表达式为 .
16. 如图,在平面直角坐标系中,点C、D的坐标分别为(2,3)、(1,0).现以原点O为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上,且OB=2,则点C的对应点A的坐标为 .
17. 已知两个直角三角形的三边长分别为3、4、m和6、8、n,且这两个直角三角形不相似,则m+n的值为 .
18. (2023·日照)如图,在矩形ABCD中,AB=6,AD=8,点P在对角线BD上,过点P作MN⊥BD,交边AD、BC于点M、N,过点M作ME⊥AD,交BD于点E,连接EN、BM、DN.有下列结论:① EM=EN;② 四边形MBND的面积不变;③ 当AM∶MD=1∶2时,S△MPE=;④ BM+MN+ND的最小值是20.其中,正确的是 (填序号).
19. (2023·云南)如图,BC是☉O的直径,A是☉O上异于点B、C的点.☉O外的点E在射线CB上,直线EA与CD垂直,垂足为D,连接AB、AC,且DA·AC=DC·AB.
(1) 求证:直线EA是☉O的切线;
(2) 若BC=BE,S△ACD=mS△BAE,求常数m的值.
第19题
20. 若一个三角形一条边的长的平方等于另外两条边的长的乘积,则我们把这个三角形叫做比例三角形.
(1) 已知△ABC是比例三角形,AB=2,BC=3,求出所有满足条件的AC的长.
(2) 如图①,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠CDA.求证:△ABC是比例三角形.
(3) 如图②,在(2)的条件下,当∠CDA=90°时,求的值.
第20题
第6章整合提升
1. D
2. 0.618 解析:∵ E是AD的黄金分割点,且DE≈0.618AD,∴ =≈0.618.根据题意,得EG=AE,∴ ≈0.618.∴ EG≈0.618DE.
3. C 4. D 5. 12 6. 5 7. -15
8. (1) 连接OC.∵ l是☉O的切线,∴ OC⊥l.∴ ∠OCD=90°.∵ AD⊥l,∴ ∠ADC=90°.∴ ∠OCD+∠ADC=180°.∴ OC∥AD.∴ ∠CAD=∠ACO.∵ OA=OC,∴ ∠BAC=∠ACO.∴ ∠CAD=∠BAC.∵ AB为☉O的直径,∴ ∠ACB=90°.∴ ∠ACB=∠ADC.∴ △ABC∽△ACD (2) ∵ 在Rt△ADC中,AC=5,CD=4,∴ AD==3.∵ △ABC∽△ACD,∴ =.∴ =.∴ AB=.∴ ☉O的半径为AB=
9. (1) ∵ AC=AB,∴ ∠C=∠B.∵ CF=BE,∴ CF-EF=BE-EF,即CE=BF.在△ACE和△ABF中,∴ △ACE≌△ABF.∴ ∠CAE=∠BAF (2) ∵ △ACE≌△ABF,∴ AE=AF,∠CAE=∠BAF. ∵ AE2=AQ·AB,AC=AB,∴ =.又∵ ∠CAE=∠FAQ,∴ △ACE∽△AFQ.∴ ∠AEC=∠AQF.∴ ∠AEF=∠BQF.∵ AE=AF,∴ ∠AEF=∠AFE.∴ ∠AFE=∠BQF.又∵ ∠C=∠B,∴ △CAF∽△BFQ.∴ =,即CF·FQ=AF·BQ
10. (4,6) 11. A 12. 14
13. A 解析:过点A作AE⊥l3于点E,交l2于点G.由l1∥l2∥l3,得==,即CD=3AD.设AD=a,则CD=3a,AC=CD+AD=4a.由题意,得BC=AC,∴ BC=4a.在Rt△BCD中,由勾股定理,得BD==5a.在Rt△ABC中,AB==4a.∴ =.
14. C
15. 2 y= 解析:证△APQ∽△ADC,得=,代入AC=2,x=y,可求CD=2.设DE=t,则AP=2t,证△APQ∽△ADC,得==.∴ CD=,AD=.证△CDE∽△BAE,得=,即=,整理,得y=.
16. (4,6)或(-4,-6)
17. 5+2或10+ 解析:当3、4为直角边长,6、8也为直角边长时,两个直角三角形相似,不合题意;当3、4为直角边长,易得m=5时,8为另一个直角三角形的斜边长,由勾股定理,得其另一直角边长为=2,此时m+n=5+2;当6、8为直角边长,易得n=10时,4为另一个直角三角形的斜边长,由勾股定理,得其另一直角边长为=,此时m+n=10+.综上所述,m+n的值为5+2或10+.
18. ②③④
19. (1) 连接OA.∵ DA·AC=DC·AB,∴ =.∵ BC是☉O的直径,∴ ∠BAC=90°.∵ EA⊥CD,∴ ∠ADC=90°.∴ ∠BAC=∠ADC.∴ △ABC∽△DAC.∴ ∠ACB=∠DCA.∵ OA=OC,∴ ∠OAC=∠ACB.∴ ∠OAC=∠DCA.∴ OA∥CD.∴ ∠OAE=∠ADC=90°.∴ OA⊥DE.又∵ OA为☉O的半径,∴ 直线EA是☉O的切线 (2) ∵ BC=BE,∴ S△BAE=S△ABC=S△ACE.∵ OB=OA,∴ ∠OBA=∠OAB.∵ ∠BAC=90°,∠OAE=90°,∴ ∠OBA +∠ACE=90°,∠OAB +∠BAE=90°.∴ ∠ACE=∠BAE.又∵ ∠E=∠E,∴ △ACE∽△BAE.∴ ==2.设BA2=x,则AC2=2x.∴ 在Rt△ABC中,BC2=AC2+BA2=3x.∴ ==.由(1),得△ABC∽△DAC,∴ ==,即=.∴ S△ACD=S△BAE.∴ m=
20. (1) 由题意,分三种情况讨论:① AC2=AB·BC,∴ AC=(负值舍去);② AB2=AC·BC,∴ AC=;③ BC2=AB·AC,∴ AC=.综上所述,AC的长为或或 (2) ∵ AD∥BC,∴ ∠ACB=∠DAC.又∵ ∠BAC=∠CDA,∴ △ABC∽△DCA.∴ =,即CA2=BC·AD.∵ AD∥BC,∴ ∠ADB=∠CBD.∵ BD平分∠ABC,∴ ∠ABD=∠CBD.∴ ∠ADB=∠ABD.∴ AD=AB.∴ CA2=BC·AB.∴ △ABC是比例三角形 (3) 过点A作AH⊥BD于点H.∵ AD=AB,AH⊥BD,∴ ∠BHA=90°,BH=BD.∵ AD∥BC,∠CDA=90°,∴ ∠BCD=180°-∠CDA=90°.∴ ∠BHA=∠BCD=90°.又∵ ∠ABH=∠DBC,∴ △ABH∽△DBC.∴ =,即AB·BC=BH·DB.∴ AB·BC=BD2.又∵ AB·BC=AC2,∴ BD2=AC2.∴ =
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
