第7章 锐角三角函数 专题练习 (含答案)2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 第7章 锐角三角函数 专题练习 (含答案)2024-2025学年数学苏科版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 310.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 16:45:41 | ||
图片预览

文档简介
第7章 锐角三角函数
小专题(六) 添设辅助线构造直角三角形解题
类型一 无直角的三角形作高构造直角三角形
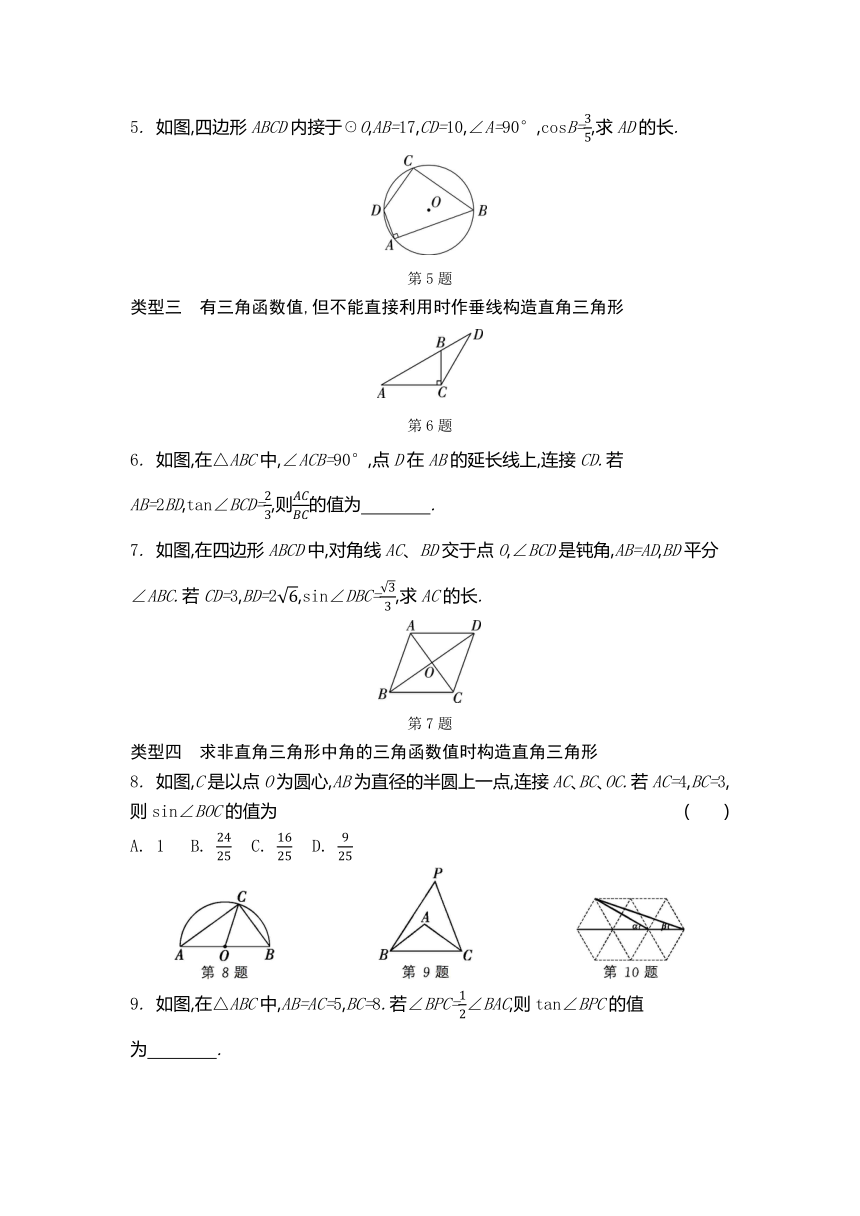
1. 如图,△ABC的底边BC上的高为h1,△PQR的底边QR上的高为h2,则有 ( )
A. h1=h2 B. h1h2 D. 以上都有可能
小专题(六) 添设辅助线构造直角三角形解题
类型一 无直角的三角形作高构造直角三角形
1. 如图,△ABC的底边BC上的高为h1,△PQR的底边QR上的高为h2,则有 ( )
A. h1=h2 B. h1
h2 D. 以上都有可能
2. (2024·海南)如图,菱形ABCD的边长为2,∠ABC=120°,边AB在数轴上,将AC绕点A按顺时针方向旋转,点C落在数轴上的点E处.若点E表示的数是3,则点A表示的数是 ( )
A. 1 B. 1- C. 0 D. 3-2
3. (2023·济宁)如图,△ABC是边长为6的等边三角形,点D、E在边BC上.若∠DAE=30°,tan∠EAC=,则BD的长为 .
第4题
类型二 有直角、无三角形的图形延长某些边构造直角三角形
4. 如图,在四边形ABCD中,AB=2,CD=1,∠B=∠D=90°,∠A=60°,则四边形ABCD的面积为 .
5. 如图,四边形ABCD内接于☉O,AB=17,CD=10,∠A=90°,cosB=,求AD的长.
第5题
类型三 有三角函数值,但不能直接利用时作垂线构造直角三角形
第6题
6. 如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD.若AB=2BD,tan∠BCD=,则的值为 .
7. 如图,在四边形ABCD中,对角线AC、BD交于点O,∠BCD是钝角,AB=AD,BD平分∠ABC.若CD=3,BD=2,sin∠DBC=,求AC的长.
第7题
类型四 求非直角三角形中角的三角函数值时构造直角三角形
8. 如图,C是以点O为圆心,AB为直径的半圆上一点,连接AC、BC、OC.若AC=4,BC=3,则sin∠BOC的值为 ( )
A. 1 B. C. D.
9. 如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,则tan∠BPC的值为 .
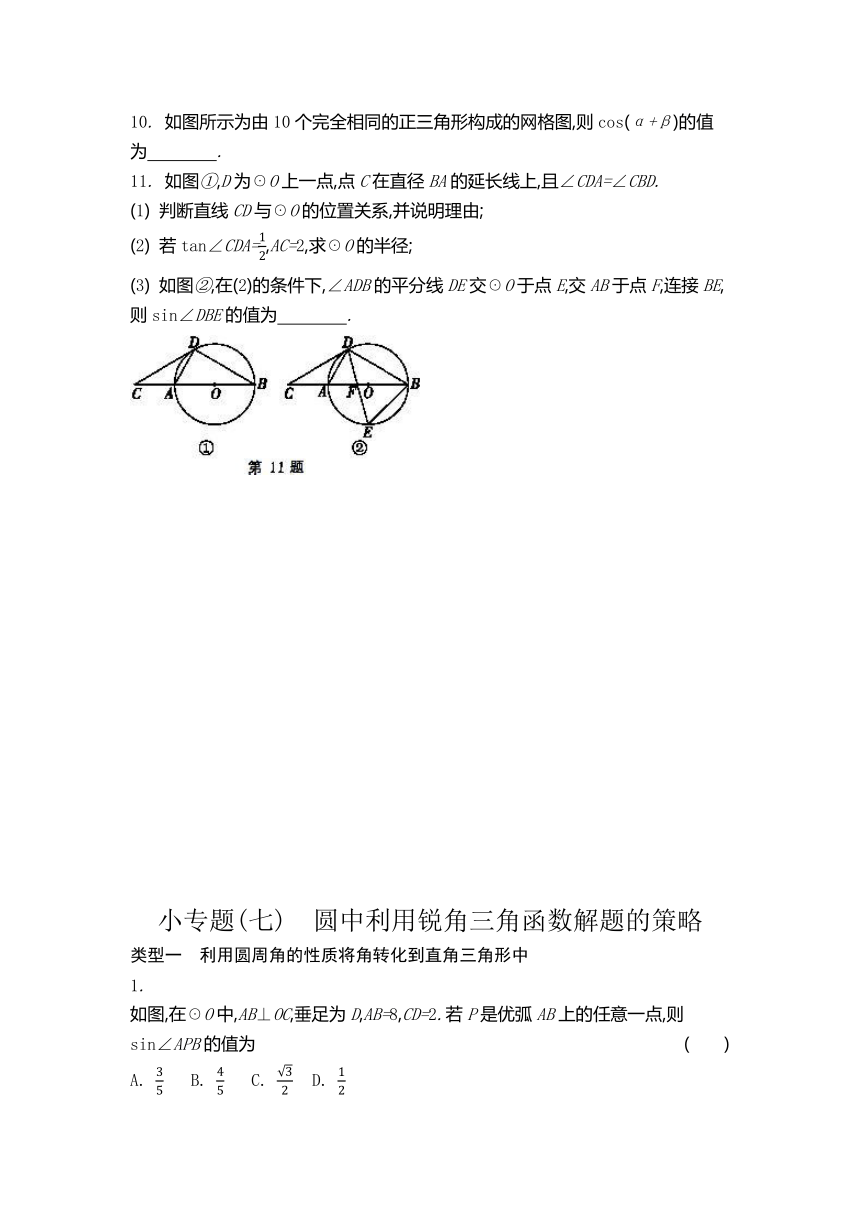
10. 如图所示为由10个完全相同的正三角形构成的网格图,则cos(α+β)的值为 .
11. 如图①,D为☉O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1) 判断直线CD与☉O的位置关系,并说明理由;
(2) 若tan∠CDA=,AC=2,求☉O的半径;
(3) 如图②,在(2)的条件下,∠ADB的平分线DE交☉O于点E,交AB于点F,连接BE,则sin∠DBE的值为 .
小专题(七) 圆中利用锐角三角函数解题的策略
类型一 利用圆周角的性质将角转化到直角三角形中
1.
如图,在☉O中,AB⊥OC,垂足为D,AB=8,CD=2.若P是优弧AB上的任意一点,则sin∠APB的值为 ( )
A. B. C. D.
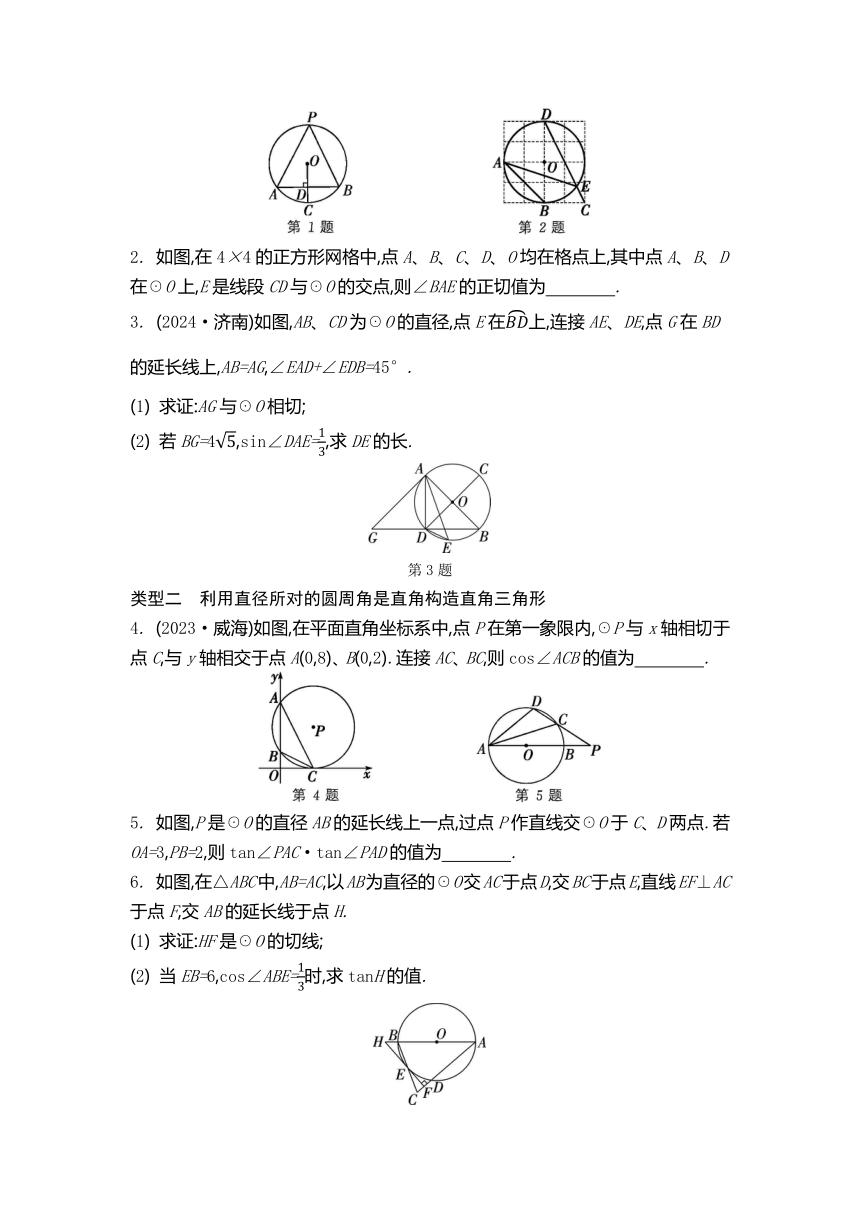
2. 如图,在4×4的正方形网格中,点A、B、C、D、O均在格点上,其中点A、B、D在☉O上,E是线段CD与☉O的交点,则∠BAE的正切值为 .
3. (2024·济南)如图,AB、CD为☉O的直径,点E在上,连接AE、DE,点G在BD的延长线上,AB=AG,∠EAD+∠EDB=45°.
(1) 求证:AG与☉O相切;
(2) 若BG=4,sin∠DAE=,求DE的长.
第3题
类型二 利用直径所对的圆周角是直角构造直角三角形
4. (2023·威海)如图,在平面直角坐标系中,点P在第一象限内,☉P与x轴相切于点C,与y轴相交于点A(0,8)、B(0,2).连接AC、BC,则cos∠ACB的值为 .
5. 如图,P是☉O的直径AB的延长线上一点,过点P作直线交☉O于C、D两点.若OA=3,PB=2,则tan∠PAC·tan∠PAD的值为 .
6. 如图,在△ABC中,AB=AC,以AB为直径的☉O交AC于点D,交BC于点E,直线EF⊥AC于点F,交AB的延长线于点H.
(1) 求证:HF是☉O的切线;
(2) 当EB=6,cos∠ABE=时,求tanH的值.
第6题
7. 如图,AD是☉O的直径,BD、BC都是弦,且BD=BC,经过点B作☉O的切线,交AD的延长线于点E.
(1) 求证:∠EBD=∠CAB;
(2) 若BC=,AC=5,求sin∠CBA的值.
第7题
类型三 利用切线与相关半径的关系构造直角三角形
8. (2023·武汉)如图,在四边形ABCD中,AB∥CD,AD⊥AB,以点D为圆心、AD长为半径的弧恰好与BC相切,切点为E.若=,则sinC的值为 .
9. 如图,半径为的☉O与边长为8的等边三角形ABC的两边AB、BC都相切,连接OC,则tan∠OCB的值为 .
小专题(六) 添设辅助线构造
直角三角形解题
1. A 2. D 3. 3-
4. 解析:延长AD、BC交于点E.∵ ∠B=90°,∠A=60°,AB=2,∴ 在Rt△ABE中,∠E=90°-∠A=30°,AE==4.∵ ∠CDE=90°,∠E=30°,CD=1,∴ 在Rt△CDE中,CE==2.在Rt△ABE中,由勾股定理,得BE===2.在Rt△CDE中,由勾股定理,得DE===.∴ S四边形ABCD=S△ABE-S△CDE=×2×2-××1=.
5. 延长AD、BC交于点E.∵ 四边形ABCD内接于☉O,∴ ∠B+∠ADC=180°,∠A+∠BCD=180°.∵ ∠A=90°,∠ADC+∠EDC=180°,∠ECD+∠BCD=180°,∴ ∠ECD=∠A=90°,∠B=∠EDC.∵ cosB=,∴ cos∠EDC=.∵ 在Rt△ECD中,cos∠EDC=,CD=10,∴ ED=.∵ 在Rt△EAB中,cosB==,AB=17,∴ BE=.∴ 由勾股定理,得AE==.∴ AD=AE-ED=-=6
6. 2 解析:过点D作DM⊥BC,交CB的延长线于点M.由tan∠BCD==,设DM=2k(k>0),则CM=3k.证△DBM∽△ABC,得===,∴ 易得BC=2k,AC=4k,则==2.
7. 过点D作DE⊥BC,交BC的延长线于点E,则∠E=90°.∵ 在Rt△BED中,sin∠DBC==,BD=2,∴ DE=2.∴ BE==4.在Rt△DCE中,∵ CD=3,∴ CE==1.∴ BC=BE-CE=3.∴ BC=CD.∴ ∠CBD=∠CDB.∵ BD平分∠ABC,∴ ∠ABD=∠CBD.∴ ∠ABD=∠CDB.∴ AB∥CD.∵ AB=AD,∴ ∠ABD=∠ADB.∴ ∠ADB=∠DBC.∴ AD∥BC.∴ 四边形ABCD是平行四边形.又∵ AB=AD,∴ 四边形ABCD是菱形.∴ AC⊥BD,AO=CO,BO=DO=BD=.∴ 在Rt△BOC中,OC==.∴ AC=2OC=2
8. B 9. 10.
11. (1) CD与☉O相切 理由:连接OD.∵ OD=OB,∴ ∠ODB=∠CBD.∵ ∠CDA=∠CBD,∴ ∠CDA=∠ODB.∵ AB为☉O的直径,∴ ∠ADB=∠ADO+∠ODB=90°.∴ ∠ADO+∠CDA=90°.∴ ∠CDO=90°,即OD⊥CD.∵ OD是☉O的半径,∴ CD与☉O相切. (2) ∵ ∠CDA=∠CBD,tan∠CDA=,∴ tan∠CBD=.∴ 在Rt△ADB中,tan∠CBD==.∵ ∠C=∠C,∠CDA=∠CBD,∴ △CAD∽△CDB.∴ ===.∴ CD=2CA=4.∴ CB=2CD=8.∴ AB=CB-CA=8-2=6.∴ OA=OB=AB=3,即☉O的半径为3
(3) 解析:连接OE,过点E作EG⊥BD于点G.∵ DE平分∠ADB,∴ ∠ADE=∠BDE=45°.∵ =,∴ ∠BOE=2∠BDE=90°.∴ 在Rt△BOE中,由勾股定理,得BE==3.∵ 在Rt△ABD中,由勾股定理,得AD2+BD2=AB2=62,=,∴ AD=,BD=.∵ EG⊥BD,∠BDE=45°,∴ ∠DEG=45°=∠BDE.∴ DG=EG.设DG=x,则EG=x,BG=BD-DG=-x.在Rt△BEG中,由勾股定理,得EG2+BG2=BE2,∴ x2+=(3)2,即5x2-12x+27=0,解得x1=,x2=(不合题意,舍去).∴ EG=.∴ 在Rt△BGE中,sin∠DBE==.
小专题(七) 圆中利用锐角三角函数
解题的策略
1. B 2.
3. (1) ∵ =,∴ ∠EDB=∠EAB.∵ ∠EAD+∠EDB=45°,∴ ∠EAD+∠EAB=45°,即∠BAD=45°.∵ AB为☉O的直径,∴ ∠ADB=90°.∴ ∠B=45°.∵ AB=AG,∴ ∠B=∠G=45°.∴ ∠GAB=90°.∵ AB为☉O的直径,∴ AG与☉O相切 (2) 连接CE.∵ 在Rt△BAG中,∠B=45°,BG=4,∴ AB=BG·cos45°=4×=2.∴ DC=2.∵ =,∴ ∠DAE=∠DCE.∵ DC为☉O的直径,∴ ∠DEC=90°.∴ 在Rt△DEC中,sin∠DCE=sin∠DAE==.∴ DE=DC·sin∠DAE=2×=
4. 5.
6. (1) 连接OE、AE.∵ AB为☉O的直径,∴ ∠AEB=90°,即AE⊥BC.∵ AB=AC,∴ 易得BE=CE.∵ OB=OA,∴ OE∥AC.又∵ HF⊥AC,∴ OE⊥HF.∵ OE是☉O的半径,∴ HF是☉O的切线 (2) 过点E作EG⊥AH于点G.∵ 在Rt△BGE中,cos∠ABE=,EB=6,∴ BG=EB·cos∠ABE=2.∴ EG==4.∵ 在Rt△BEA中,cos∠ABE=,EB=6,∴ AB==18.∴ OB=OE=AB=9.∴ GO=OB-BG=7.∵ EG⊥AH,OE⊥HF,∴ ∠H+∠HEG=90°,∠GEO+∠HEG=90°.∴ ∠H=∠GEO.∴ 在Rt△EGO中,tanH=tan∠GEO===
7. (1) 连接OB.∵ BE是☉O的切线,∴ OB⊥BE.∴ ∠OBD+∠EBD=90°.∵ AD是☉O的直径,∴ ∠ABD=90°.∴ ∠ABO+∠OBD=90°.∴ ∠EBD=∠ABO.∵ OA=OB,∴ ∠OAB=∠ABO.∴ ∠OAB=∠EBD.∵ BD=BC,∴ =.∴ ∠BAD=∠CAB.∴ ∠EBD=∠CAB (2) 连接CD,交OB于点M.∵ =,∴ CM=MD,OB⊥CD.又∵ OA=OD,∴ OM为△ACD的中位线.∴ OM=AC=.设☉O的半径为r,则BM=r-.∴ 在Rt△OMD和Rt△BMD中,由勾股定理,得DM2=OD2-OM2=BD2-BM2.∵ BD=BC=,∴ r2-=()2-,解得r=3(负值舍去).∴ AD=2r=6.∵ AD是☉O的直径,∴ ∠ACD=90°.∴ 在Rt△ACD中,sin∠ADC==.∵ =,∴ ∠CBA=∠ADC.∴ sin∠CBA=
8.
9. 解析:设☉O与边BC相切于点D,连接OB、OD.∵ ☉O与等边三角形ABC的两边AB、BC都相切,∴ 易得∠OBC=∠OBA=∠ABC=30°,∠ODB=90°.∵ 在Rt△OBD中,tan∠OBD=,∴ BD===3.∴ CD=BC-BD=8-3=5.∴ 在Rt△OCD中,tan∠OCB==.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
