期中素能测评(含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 期中素能测评(含答案) 2024-2025学年数学苏科版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 312.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 16:21:42 | ||
图片预览




文档简介
期中素能测评
一、 选择题(每小题3分,共24分)
1.
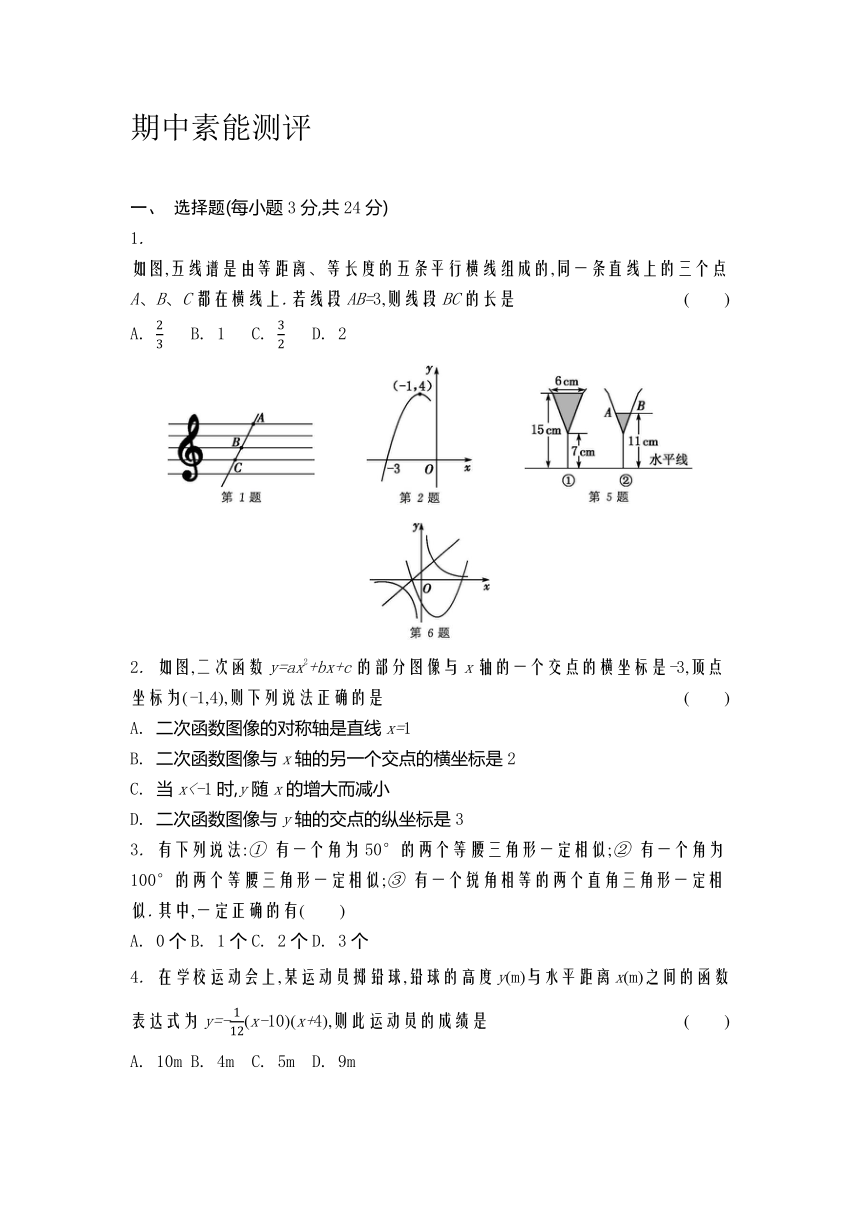
如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A、B、C都在横线上.若线段AB=3,则线段BC的长是 ( )
A. B. 1 C. D. 2
2. 如图,二次函数y=ax2+bx+c的部分图像与x轴的一个交点的横坐标是-3,顶点坐标为(-1,4),则下列说法正确的是 ( )
A. 二次函数图像的对称轴是直线x=1
B. 二次函数图像与x轴的另一个交点的横坐标是2
C. 当x<-1时,y随x的增大而减小
D. 二次函数图像与y轴的交点的纵坐标是3
3. 有下列说法:① 有一个角为50°的两个等腰三角形一定相似;② 有一个角为100°的两个等腰三角形一定相似;③ 有一个锐角相等的两个直角三角形一定相似.其中,一定正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
4. 在学校运动会上,某运动员掷铅球,铅球的高度y(m)与水平距离x(m)之间的函数表达式为y=-(x-10)(x+4),则此运动员的成绩是 ( )
A. 10m B. 4m C. 5m D. 9m
5. 如图①所示为装了液体的高脚杯示意图,用去一部分液体后如图②所示,此时液面宽AB为 ( )
A. 1cm B. 2cm C. 3cm D. 4cm
6. 一次函数y=x-2n+4、二次函数y=x2+(n-1)x-3、反比例函数y=在同一平面直角坐标系中的图像如图所示,则n的取值范围是 ( )
A. n>-1 B. n>2
C. -17. 如图,在△ABC中,D是边BC上的点(不与点B、C重合).过点D作DE∥AB,交AC于点E;过点D作DF∥AC,交AB于点F.设N是线段BF上的点,BN=2NF;M是线段DE上的点,DM=2ME,连接EF、MN、MC、NC.若已知△CMN的面积,则一定能求出 ( )
A. △AFE的面积 B. △BDF的面积 C. △BCN的面积 D. △DCE的面积
8. 如图,二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图像与x轴交于点A,对称轴是直线x=-.有下列结论:① abc<0;② 若点(-1,y1)和点(2,y2)都在抛物线上,则y1A. 1个 B. 2个 C. 3个 D. 4个
二、 填空题(每小题3分,共24分)
9. 若==(a≠c≠0),则的值为 .
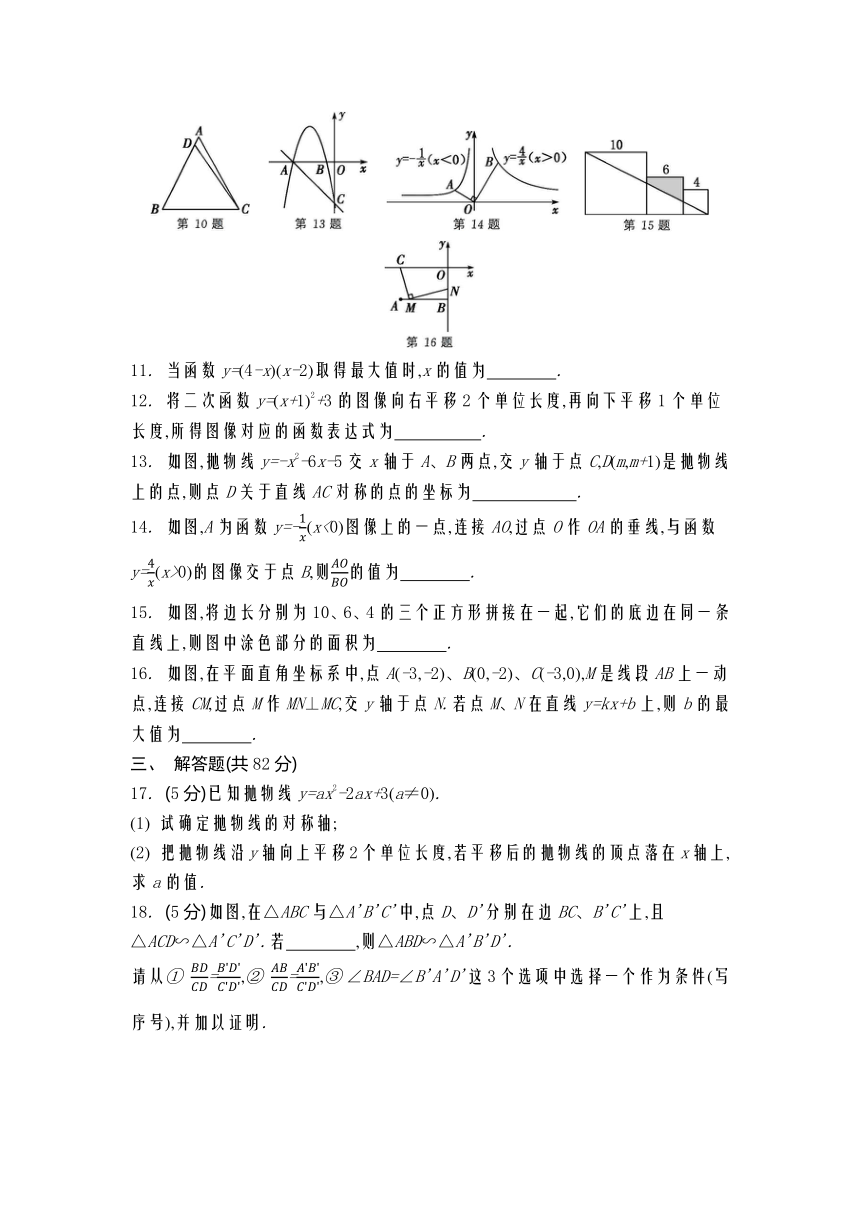
10. 如图,在△ABC中,D为边AB上一点,且∠BCD=∠A.如果BC=2,AB=3,那么BD= .
11. 当函数y=(4-x)(x-2)取得最大值时,x的值为 .
12. 将二次函数y=(x+1)2+3的图像向右平移2个单位长度,再向下平移1个单位长度,所得图像对应的函数表达式为 .
13. 如图,抛物线y=-x2-6x-5交x轴于A、B两点,交y轴于点C,D(m,m+1)是抛物线上的点,则点D关于直线AC对称的点的坐标为 .
14. 如图,A为函数y=-(x<0)图像上的一点,连接AO,过点O作OA的垂线,与函数y=(x>0)的图像交于点B,则的值为 .
15. 如图,将边长分别为10、6、4的三个正方形拼接在一起,它们的底边在同一条直线上,则图中涂色部分的面积为 .
16. 如图,在平面直角坐标系中,点A(-3,-2)、B(0,-2)、C(-3,0),M是线段AB上一动点,连接CM,过点M作MN⊥MC,交y轴于点N.若点M、N在直线y=kx+b上,则b的最大值为 .
三、 解答题(共82分)
17. (5分)已知抛物线y=ax2-2ax+3(a≠0).
(1) 试确定抛物线的对称轴;
(2) 把抛物线沿y轴向上平移2个单位长度,若平移后的抛物线的顶点落在x轴上,求a的值.
18. (5分)如图,在△ABC与△A'B'C'中,点D、D'分别在边BC、B'C'上,且△ACD∽△A'C'D'.若 ,则△ABD∽△A'B'D'.
请从① =,② =,③ ∠BAD=∠B'A'D'这3个选项中选择一个作为条件(写序号),并加以证明.
19. (6分)如图,△ABC的三个顶点坐标分别为A(-2,-2)、B(-5,-4)、C(-1,-5).
(1) 画出△ABC关于x轴对称的△A1B1C1(点A、B、C的对应点分别为A1、B1、C1).
(2) 以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2(点A、B、C的对应点分别为A2、B2、C2).
(3) ① 点B2的坐标为 ;
② △A2B2C2的面积为 .
20. (6分)已知点(-m,0)、(3m,0)在二次函数y=ax2+bx+3(a、b是常数,a≠0)的图像上.
(1) 当m=-1时,求a和b的值;
(2) 若二次函数的图像经过点A(n,3)且点A不在坐标轴上,当-221. (6分)已知二次函数y=2(x-1)(x-m-3)(m为常数).
(1) 求证:不论m为何值,该函数的图像与x轴总有公共点;
(2) 当m取什么值时,该函数的图像与y轴的交点在x轴的上方
22. (8分)如图,二次函数y=x2+bx+c的图像与x轴交于A、B两点,与y轴交于点C,其中A(-2,0)、C(0,-2).
(1) 求二次函数的表达式;
(2) 若P是二次函数图像上的一点,且点P在第二象限,线段PC交x轴于点D,△PDB的面积是△CDB的面积的2倍,求点P的坐标.
第22题
23. (8分)如图,AB是☉O的直径,E为☉O上一点,D是上一点,连接AD、DE,连接AE并延长至点C,连接BC,使∠CBE=∠BDE,BD与AE交于点F.
(1) 求证:BC是☉O的切线;
(2) 若BD平分∠ABE,求证:AD2=DF·BD.
第23题
24. (8分)在如图所示的平面直角坐标系中,有一斜坡OA,从点O处抛出一个小球,落到点A处.小球在空中所经过的路线是抛物线y=-x2+bx的一部分.
(1) 求抛物线对应的函数表达式;
(2) 求抛物线最高点的坐标;
(3) 斜坡上点B处有一棵树,B是OA的三等分点,小球恰好越过树的顶端C,求这棵树的高度.
第24题
25. (10分)如图,在△ABC中,∠BAC=90°,AB=AC,D是边AB上不与点A、B重合的一个定点.AO⊥BC于点O,交CD于点E,DF是由线段DC绕点D按顺时针方向旋转90°得到的,FD、CA的延长线相交于点M,连接BF、CF.
(1) 求证:△ADE∽△FMC;
(2) 求∠ABF的度数.
第25题
26. (10分)如图,点A、B、M、E、F依次在直线l上,点A、B固定不动,且AB=2,分别以AB、EF为边在直线l同侧作正方形ABCD、正方形EFGH,∠PMN=90°,直角边MP恒过点C,直角边MN恒过点H.
(1) 若BE=10,EF=12,求点M与点B之间的距离;
(2) 若BE=10,当点M在点B、E之间运动时,求HE长的最大值.
第26题
27. (10分)如图,抛物线y=ax2-2x+c(a≠0)与x轴交于A、B(3,0)两点,与y轴交于点C(0,-3),抛物线的顶点为D.
(1) 求抛物线对应的函数表达式.
(2) 点P在抛物线的对称轴上,点Q在x轴上.若以P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标.
(3) 若M是x轴上的动点,过点M作x轴的垂线,交抛物线于点G,是否存在这样的点M,使得以A、M、G为顶点的三角形与△BCD相似 若存在,请求出点M的坐标;若不存在,请说明理由.
第27题
期中素能测评
一、 1. C 2. D 3. C 4. A 5. C 6. C 7. D 8. B
二、 9. 10. 11. 3 12. y=(x-1)2+2 13. (0,1)或(-5,-4) 14. 15. 15
16. - 解析:设BN=y,AM=x,则MB=3-x,ON=2-y.连接AC,则易得四边形ABOC是矩形.证△AMC∽△BNM,得=,即=,∴ y=-x2+x=-x-2+.∵ -<0,∴ 当x=时,y最大值=.∵ 直线y=kx+b与y轴交于点N(0,b),∴ 当BN长的值最大,即ON长的值最小时,b的值最大,此时ON=OB-BN=2-=.∴ N0,-.∴ b的最大值为-.
三、 17. (1) ∵ -=1,∴ 抛物线的对称轴为直线x=1 (2) 把抛物线y=ax2-2ax+3沿y轴向上平移2个单位长度,可得平移后的抛物线对应的函数表达式为y'=ax2-2ax+5.此时抛物线顶点的纵坐标为=5-a.∵ 平移后的抛物线的顶点落在x轴上,∴ 5-a=0,解得a=5,即a的值为5
18. 答案不唯一,如选③ ∵ △ACD∽△A'C'D',∴ ∠ADC=∠A'D'C'.∵ ∠ADC+∠ADB=180°,∠A'D'C'+∠A'D'B'=180°,∴ ∠ADB=∠A'D'B'.又∵ ∠BAD=∠B'A'D',∴ △ABD∽△A'B'D'
19. (1) 如图,△A1B1C1即为所求 (2) 如图,△A2B2C2即为所求 (3) ① (10,8)
② 22 解析:△A2B2C2的面积为8×6-×2×6-×8×2-×6×4=22.
20. (1) 当m=-1时,二次函数y=ax2+bx+3的图像过点(1,0)和(-3,0),∴ 解得∴ a的值是-1,b的值是-2 (2) ∵ 二次函数y=ax2+bx+3的图像过点(-m,0)和(3m,0),∴ 抛物线的对称轴为直线x=m.∵ 图像过点A(n,3)、(0,3),且点A不在坐标轴上,∴ 由图像的对称性,得m=n.∵ -221. (1) 当y=0时,2(x-1)(x-m-3)=0,解得x1=1,x2=m+3.∴ 该函数的图像过定点(1,0).∴ 不论m为何值,该函数的图像与x轴总有公共点 (2) 当x=0时,y=2m+6,即该函数的图像与y轴交点的纵坐标为2m+6.∴ 当2m+6>0,即m>-3时,该函数的图像与y轴的交点在x轴的上方
22. (1) 将A(-2,0)、C(0,-2)代入y=x2+bx+c,得解得∴ 二次函数的表达式为y=x2+x-2 (2) 由题意,设P(m,n).∵ 点P在第二象限,∴ m<0,n>0.∵ △PDB的面积是△CDB的面积的2倍,即=2,∴ =2.∴ =2.由C(0,-2),得CO=2,∴ n=2CO=4.∵ P(m,4)是二次函数y=x2+x-2的图像上的点,∴ m2+m-2=4,解得m1=-3,m2=2(不合题意,舍去).∴ 点P的坐标为(-3,4)
23. (1) ∵ AB是☉O的直径,∴ ∠AEB=90°.∴ ∠EAB+∠EBA=90°.∵ ∠CBE=∠BDE,∠BDE=∠EAB,∴ ∠EAB=∠CBE.∴ ∠EBA+∠CBE=90°,即∠ABC=90°.∴ CB⊥AB.∵ AB是☉O的直径,∴ BC是☉O的切线 (2) ∵ BD平分∠ABE,∴ ∠DBA=∠DBE.∵ ∠DAF=∠DBE,∴ ∠DAF=∠DBA.又∵ ∠FDA=∠ADB,∴ △ADF∽△BDA.∴ =.∴ AD2=DF·BD
24. (1) ∵ A是抛物线y=-x2+bx上的一点,∴ =-32+3b,解得b=.∴ 抛物线对应的函数表达式为y=-x2+x (2) ∵ y=-x2+x=-+,∴ 抛物线最高点的坐标为 (3) 如图,过点A、B分别作x轴的垂线,垂足分别是E、D,则易知C、B、D三点共线,∠BDO=∠AEO=90°.又∵ ∠BOD=∠AOE,∴ △OBD∽△OAE.∴ ==.又∵ B是OA的三等分点,∴ =.∴ ==.∵ A,∴ AE=,OE=3.∴ BD=,OD=1.∴ 点C的横坐标为1.将x=1代入y=-x2+x,得y=.∴ 点C的坐标为.∴ CD=.∴ CB=CD-BD=-=2.∴ 这棵树的高度是2
25. (1) ∵ DF是由线段DC绕点D按顺时针方向旋转90°得到的,∴ ∠FDC=90°,FD=CD.∴ ∠DFC=45°.∵ AB=AC,AO⊥BC,∴ ∠BAO=∠BAC.∵ ∠BAC=90°,∴ ∠BAO=∠ABC=45°.∴ ∠BAO=∠DFC.∵ ∠EDA+∠ADM=90°,∠M+∠ADM=90°,∴ ∠EDA=∠M.∴ △ADE∽△FMC (2) 设BC与DF的交点为I.∵ ∠DBI=∠CFI=45°,∠BID=∠FIC,∴ △BID∽△FIC.∴ =,即=.∵ ∠BIF=∠DIC,∴ △BIF∽△DIC.∴ ∠IBF=∠IDC.∵ ∠IDC=90°,∴ ∠IBF=90°.∵ ∠ABC=45°,∴ ∠ABF=∠ABC+∠IBF=135°
26. (1) 设BM=x,则ME=10-x.∵ 四边形ABCD是正方形,∴ ∠ABC=90°,BC=AB=2.∴ ∠CBM=90°.∵ 四边形EFGH是正方形,∴ ∠HEF=90°,HE=EF=12.∴ ∠MEH=90°.∴ ∠EMH+∠EHM=90°.∵ ∠PMN=90°,∴ ∠BMC+∠EMH=90°.∴ ∠BMC=∠EHM.∵ ∠CBM=∠MEH=90°,∴ △BCM∽△EMH.∴ =,即=.整理,得x2-10x+24=0,解得x=4或6.经检验,x=4或6均是原分式方程的解,且符合题意.∴ BM=4或6.∴ 点M与点B之间的距离是4或6 (2) 由(1),得=.设EH=y,BM=x.∵ BE=10,∴ EM=10-x.∴ =.∴ y=-x2+5x=-(x-5)2+12.5.∵ -<0,∴ 当x=5时,y取得最大值,为12.5.∴ HE长的最大值为12.5
27. (1) 将B(3,0)、C(0,-3)分别代入y=ax2-2x+c(a≠0),得解得∴ 抛物线对应的函数表达式为y=x2-2x-3 (2) P(1,-3)、Q(4,0)或P(1,3)、Q(-2,0) (3) 存在 在y=x2-2x-3中,令y=0,得x1=-1,x2=3.∴ A(-1,0).又∵ y=x2-2x-3=(x-1)2-4,∴ 抛物线的顶点D的坐标为(1,-4),对称轴为直线x=1.∵ B(3,0),∴ BD2=22+42=20,CD2=12+12=2,BC2=32+32=18.∴ CD=,BC=3,BD2=CD2+BC2.∴ △BDC是直角三角形,且∠BCD=90°.假设存在满足条件的点M.设点M的坐标为(m,0),则点G的坐标为(m,m2-2m-3).根据题意,得∠AMG=∠BCD=90°.∴ 要使以A、M、G为顶点的三角形与△BCD相似,需要满足条件=或=.① 当m<-1时,有=或=,解得m1=,m2=-1或m3=0,m4=-1,都不合题意.∴ 当m<-1时,无解.② 当m=-1时,点A、M、G重合,无法构成三角形,∴ 不符合题意.③ 当-13时,有=或=,解得m9=,m10=-1(不合题意,舍去)或m11=6,m12=-1(不合题意,舍去).此时存在M或M(6,0).综上所述,存在点M,使得以A、M、G为顶点的三角形与△BCD相似,点M的坐标为或(0,0)或或(6,0)
一、 选择题(每小题3分,共24分)
1.
如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A、B、C都在横线上.若线段AB=3,则线段BC的长是 ( )
A. B. 1 C. D. 2
2. 如图,二次函数y=ax2+bx+c的部分图像与x轴的一个交点的横坐标是-3,顶点坐标为(-1,4),则下列说法正确的是 ( )
A. 二次函数图像的对称轴是直线x=1
B. 二次函数图像与x轴的另一个交点的横坐标是2
C. 当x<-1时,y随x的增大而减小
D. 二次函数图像与y轴的交点的纵坐标是3
3. 有下列说法:① 有一个角为50°的两个等腰三角形一定相似;② 有一个角为100°的两个等腰三角形一定相似;③ 有一个锐角相等的两个直角三角形一定相似.其中,一定正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
4. 在学校运动会上,某运动员掷铅球,铅球的高度y(m)与水平距离x(m)之间的函数表达式为y=-(x-10)(x+4),则此运动员的成绩是 ( )
A. 10m B. 4m C. 5m D. 9m
5. 如图①所示为装了液体的高脚杯示意图,用去一部分液体后如图②所示,此时液面宽AB为 ( )
A. 1cm B. 2cm C. 3cm D. 4cm
6. 一次函数y=x-2n+4、二次函数y=x2+(n-1)x-3、反比例函数y=在同一平面直角坐标系中的图像如图所示,则n的取值范围是 ( )
A. n>-1 B. n>2
C. -1
A. △AFE的面积 B. △BDF的面积 C. △BCN的面积 D. △DCE的面积
8. 如图,二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图像与x轴交于点A,对称轴是直线x=-.有下列结论:① abc<0;② 若点(-1,y1)和点(2,y2)都在抛物线上,则y1
二、 填空题(每小题3分,共24分)
9. 若==(a≠c≠0),则的值为 .
10. 如图,在△ABC中,D为边AB上一点,且∠BCD=∠A.如果BC=2,AB=3,那么BD= .
11. 当函数y=(4-x)(x-2)取得最大值时,x的值为 .
12. 将二次函数y=(x+1)2+3的图像向右平移2个单位长度,再向下平移1个单位长度,所得图像对应的函数表达式为 .
13. 如图,抛物线y=-x2-6x-5交x轴于A、B两点,交y轴于点C,D(m,m+1)是抛物线上的点,则点D关于直线AC对称的点的坐标为 .
14. 如图,A为函数y=-(x<0)图像上的一点,连接AO,过点O作OA的垂线,与函数y=(x>0)的图像交于点B,则的值为 .
15. 如图,将边长分别为10、6、4的三个正方形拼接在一起,它们的底边在同一条直线上,则图中涂色部分的面积为 .
16. 如图,在平面直角坐标系中,点A(-3,-2)、B(0,-2)、C(-3,0),M是线段AB上一动点,连接CM,过点M作MN⊥MC,交y轴于点N.若点M、N在直线y=kx+b上,则b的最大值为 .
三、 解答题(共82分)
17. (5分)已知抛物线y=ax2-2ax+3(a≠0).
(1) 试确定抛物线的对称轴;
(2) 把抛物线沿y轴向上平移2个单位长度,若平移后的抛物线的顶点落在x轴上,求a的值.
18. (5分)如图,在△ABC与△A'B'C'中,点D、D'分别在边BC、B'C'上,且△ACD∽△A'C'D'.若 ,则△ABD∽△A'B'D'.
请从① =,② =,③ ∠BAD=∠B'A'D'这3个选项中选择一个作为条件(写序号),并加以证明.
19. (6分)如图,△ABC的三个顶点坐标分别为A(-2,-2)、B(-5,-4)、C(-1,-5).
(1) 画出△ABC关于x轴对称的△A1B1C1(点A、B、C的对应点分别为A1、B1、C1).
(2) 以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2(点A、B、C的对应点分别为A2、B2、C2).
(3) ① 点B2的坐标为 ;
② △A2B2C2的面积为 .
20. (6分)已知点(-m,0)、(3m,0)在二次函数y=ax2+bx+3(a、b是常数,a≠0)的图像上.
(1) 当m=-1时,求a和b的值;
(2) 若二次函数的图像经过点A(n,3)且点A不在坐标轴上,当-2
(1) 求证:不论m为何值,该函数的图像与x轴总有公共点;
(2) 当m取什么值时,该函数的图像与y轴的交点在x轴的上方
22. (8分)如图,二次函数y=x2+bx+c的图像与x轴交于A、B两点,与y轴交于点C,其中A(-2,0)、C(0,-2).
(1) 求二次函数的表达式;
(2) 若P是二次函数图像上的一点,且点P在第二象限,线段PC交x轴于点D,△PDB的面积是△CDB的面积的2倍,求点P的坐标.
第22题
23. (8分)如图,AB是☉O的直径,E为☉O上一点,D是上一点,连接AD、DE,连接AE并延长至点C,连接BC,使∠CBE=∠BDE,BD与AE交于点F.
(1) 求证:BC是☉O的切线;
(2) 若BD平分∠ABE,求证:AD2=DF·BD.
第23题
24. (8分)在如图所示的平面直角坐标系中,有一斜坡OA,从点O处抛出一个小球,落到点A处.小球在空中所经过的路线是抛物线y=-x2+bx的一部分.
(1) 求抛物线对应的函数表达式;
(2) 求抛物线最高点的坐标;
(3) 斜坡上点B处有一棵树,B是OA的三等分点,小球恰好越过树的顶端C,求这棵树的高度.
第24题
25. (10分)如图,在△ABC中,∠BAC=90°,AB=AC,D是边AB上不与点A、B重合的一个定点.AO⊥BC于点O,交CD于点E,DF是由线段DC绕点D按顺时针方向旋转90°得到的,FD、CA的延长线相交于点M,连接BF、CF.
(1) 求证:△ADE∽△FMC;
(2) 求∠ABF的度数.
第25题
26. (10分)如图,点A、B、M、E、F依次在直线l上,点A、B固定不动,且AB=2,分别以AB、EF为边在直线l同侧作正方形ABCD、正方形EFGH,∠PMN=90°,直角边MP恒过点C,直角边MN恒过点H.
(1) 若BE=10,EF=12,求点M与点B之间的距离;
(2) 若BE=10,当点M在点B、E之间运动时,求HE长的最大值.
第26题
27. (10分)如图,抛物线y=ax2-2x+c(a≠0)与x轴交于A、B(3,0)两点,与y轴交于点C(0,-3),抛物线的顶点为D.
(1) 求抛物线对应的函数表达式.
(2) 点P在抛物线的对称轴上,点Q在x轴上.若以P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标.
(3) 若M是x轴上的动点,过点M作x轴的垂线,交抛物线于点G,是否存在这样的点M,使得以A、M、G为顶点的三角形与△BCD相似 若存在,请求出点M的坐标;若不存在,请说明理由.
第27题
期中素能测评
一、 1. C 2. D 3. C 4. A 5. C 6. C 7. D 8. B
二、 9. 10. 11. 3 12. y=(x-1)2+2 13. (0,1)或(-5,-4) 14. 15. 15
16. - 解析:设BN=y,AM=x,则MB=3-x,ON=2-y.连接AC,则易得四边形ABOC是矩形.证△AMC∽△BNM,得=,即=,∴ y=-x2+x=-x-2+.∵ -<0,∴ 当x=时,y最大值=.∵ 直线y=kx+b与y轴交于点N(0,b),∴ 当BN长的值最大,即ON长的值最小时,b的值最大,此时ON=OB-BN=2-=.∴ N0,-.∴ b的最大值为-.
三、 17. (1) ∵ -=1,∴ 抛物线的对称轴为直线x=1 (2) 把抛物线y=ax2-2ax+3沿y轴向上平移2个单位长度,可得平移后的抛物线对应的函数表达式为y'=ax2-2ax+5.此时抛物线顶点的纵坐标为=5-a.∵ 平移后的抛物线的顶点落在x轴上,∴ 5-a=0,解得a=5,即a的值为5
18. 答案不唯一,如选③ ∵ △ACD∽△A'C'D',∴ ∠ADC=∠A'D'C'.∵ ∠ADC+∠ADB=180°,∠A'D'C'+∠A'D'B'=180°,∴ ∠ADB=∠A'D'B'.又∵ ∠BAD=∠B'A'D',∴ △ABD∽△A'B'D'
19. (1) 如图,△A1B1C1即为所求 (2) 如图,△A2B2C2即为所求 (3) ① (10,8)
② 22 解析:△A2B2C2的面积为8×6-×2×6-×8×2-×6×4=22.
20. (1) 当m=-1时,二次函数y=ax2+bx+3的图像过点(1,0)和(-3,0),∴ 解得∴ a的值是-1,b的值是-2 (2) ∵ 二次函数y=ax2+bx+3的图像过点(-m,0)和(3m,0),∴ 抛物线的对称轴为直线x=m.∵ 图像过点A(n,3)、(0,3),且点A不在坐标轴上,∴ 由图像的对称性,得m=n.∵ -2
22. (1) 将A(-2,0)、C(0,-2)代入y=x2+bx+c,得解得∴ 二次函数的表达式为y=x2+x-2 (2) 由题意,设P(m,n).∵ 点P在第二象限,∴ m<0,n>0.∵ △PDB的面积是△CDB的面积的2倍,即=2,∴ =2.∴ =2.由C(0,-2),得CO=2,∴ n=2CO=4.∵ P(m,4)是二次函数y=x2+x-2的图像上的点,∴ m2+m-2=4,解得m1=-3,m2=2(不合题意,舍去).∴ 点P的坐标为(-3,4)
23. (1) ∵ AB是☉O的直径,∴ ∠AEB=90°.∴ ∠EAB+∠EBA=90°.∵ ∠CBE=∠BDE,∠BDE=∠EAB,∴ ∠EAB=∠CBE.∴ ∠EBA+∠CBE=90°,即∠ABC=90°.∴ CB⊥AB.∵ AB是☉O的直径,∴ BC是☉O的切线 (2) ∵ BD平分∠ABE,∴ ∠DBA=∠DBE.∵ ∠DAF=∠DBE,∴ ∠DAF=∠DBA.又∵ ∠FDA=∠ADB,∴ △ADF∽△BDA.∴ =.∴ AD2=DF·BD
24. (1) ∵ A是抛物线y=-x2+bx上的一点,∴ =-32+3b,解得b=.∴ 抛物线对应的函数表达式为y=-x2+x (2) ∵ y=-x2+x=-+,∴ 抛物线最高点的坐标为 (3) 如图,过点A、B分别作x轴的垂线,垂足分别是E、D,则易知C、B、D三点共线,∠BDO=∠AEO=90°.又∵ ∠BOD=∠AOE,∴ △OBD∽△OAE.∴ ==.又∵ B是OA的三等分点,∴ =.∴ ==.∵ A,∴ AE=,OE=3.∴ BD=,OD=1.∴ 点C的横坐标为1.将x=1代入y=-x2+x,得y=.∴ 点C的坐标为.∴ CD=.∴ CB=CD-BD=-=2.∴ 这棵树的高度是2
25. (1) ∵ DF是由线段DC绕点D按顺时针方向旋转90°得到的,∴ ∠FDC=90°,FD=CD.∴ ∠DFC=45°.∵ AB=AC,AO⊥BC,∴ ∠BAO=∠BAC.∵ ∠BAC=90°,∴ ∠BAO=∠ABC=45°.∴ ∠BAO=∠DFC.∵ ∠EDA+∠ADM=90°,∠M+∠ADM=90°,∴ ∠EDA=∠M.∴ △ADE∽△FMC (2) 设BC与DF的交点为I.∵ ∠DBI=∠CFI=45°,∠BID=∠FIC,∴ △BID∽△FIC.∴ =,即=.∵ ∠BIF=∠DIC,∴ △BIF∽△DIC.∴ ∠IBF=∠IDC.∵ ∠IDC=90°,∴ ∠IBF=90°.∵ ∠ABC=45°,∴ ∠ABF=∠ABC+∠IBF=135°
26. (1) 设BM=x,则ME=10-x.∵ 四边形ABCD是正方形,∴ ∠ABC=90°,BC=AB=2.∴ ∠CBM=90°.∵ 四边形EFGH是正方形,∴ ∠HEF=90°,HE=EF=12.∴ ∠MEH=90°.∴ ∠EMH+∠EHM=90°.∵ ∠PMN=90°,∴ ∠BMC+∠EMH=90°.∴ ∠BMC=∠EHM.∵ ∠CBM=∠MEH=90°,∴ △BCM∽△EMH.∴ =,即=.整理,得x2-10x+24=0,解得x=4或6.经检验,x=4或6均是原分式方程的解,且符合题意.∴ BM=4或6.∴ 点M与点B之间的距离是4或6 (2) 由(1),得=.设EH=y,BM=x.∵ BE=10,∴ EM=10-x.∴ =.∴ y=-x2+5x=-(x-5)2+12.5.∵ -<0,∴ 当x=5时,y取得最大值,为12.5.∴ HE长的最大值为12.5
27. (1) 将B(3,0)、C(0,-3)分别代入y=ax2-2x+c(a≠0),得解得∴ 抛物线对应的函数表达式为y=x2-2x-3 (2) P(1,-3)、Q(4,0)或P(1,3)、Q(-2,0) (3) 存在 在y=x2-2x-3中,令y=0,得x1=-1,x2=3.∴ A(-1,0).又∵ y=x2-2x-3=(x-1)2-4,∴ 抛物线的顶点D的坐标为(1,-4),对称轴为直线x=1.∵ B(3,0),∴ BD2=22+42=20,CD2=12+12=2,BC2=32+32=18.∴ CD=,BC=3,BD2=CD2+BC2.∴ △BDC是直角三角形,且∠BCD=90°.假设存在满足条件的点M.设点M的坐标为(m,0),则点G的坐标为(m,m2-2m-3).根据题意,得∠AMG=∠BCD=90°.∴ 要使以A、M、G为顶点的三角形与△BCD相似,需要满足条件=或=.① 当m<-1时,有=或=,解得m1=,m2=-1或m3=0,m4=-1,都不合题意.∴ 当m<-1时,无解.② 当m=-1时,点A、M、G重合,无法构成三角形,∴ 不符合题意.③ 当-1
同课章节目录
