专题(二) 图形的相似 (含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 专题(二) 图形的相似 (含答案) 2024-2025学年数学苏科版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览

文档简介
专题(二) 图形的相似
1. 已知===k,则k的值是 ( )
A. -1 B. 2
C. -1或2 D. 无法确定
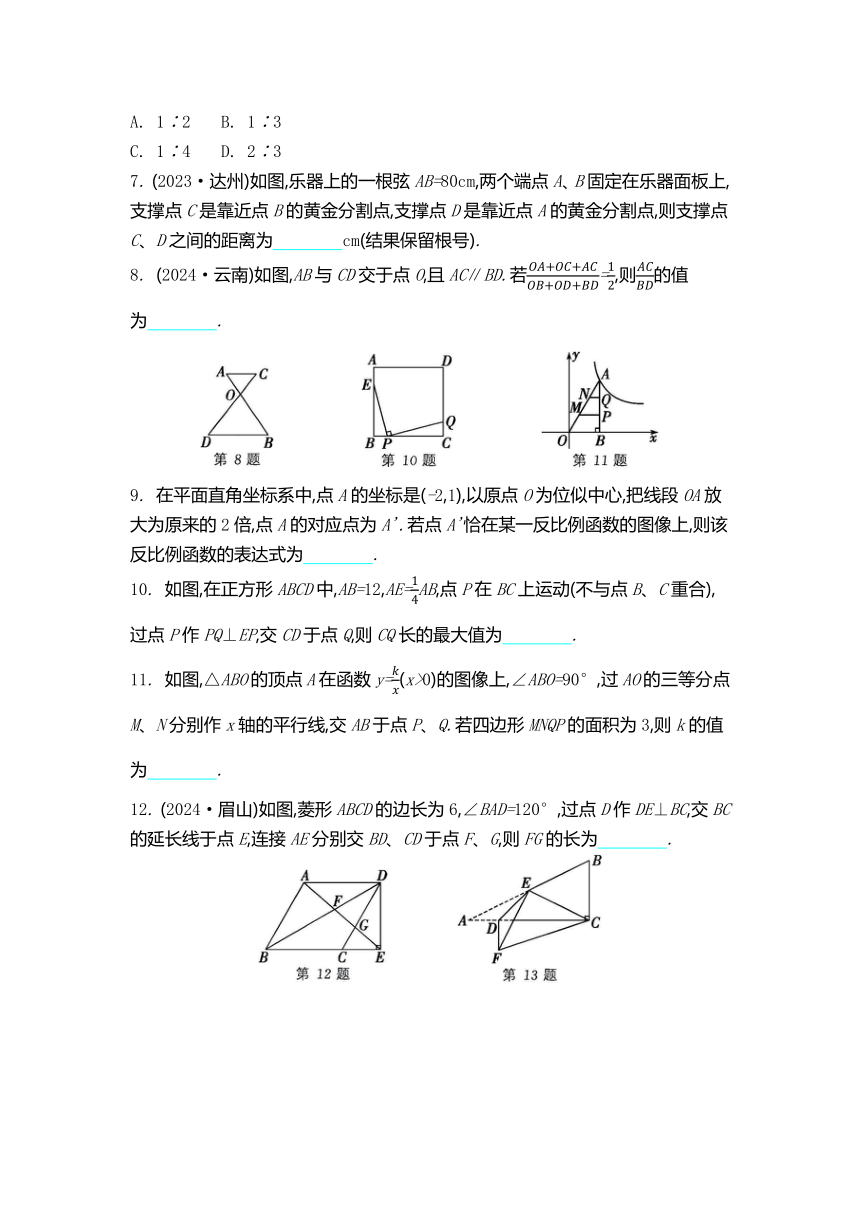
2. 如图,△ABC与△DEF位似,点O为位似中心,相似比为.若△ABC的周长为4,则△DEF的周长为 ( )
A. 4 B. 6 C. 9 D. 16
3. 如图,P为线段AB上一点,AD与BC相交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中的相似三角形有 ( )
A. 1对 B. 2对 C. 3对 D. 4对
4. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心、CA长为半径的☉C与AB交于点D,则AD的长为 ( )
A. B. C. D.
5. (2024·自贡)如图,在矩形ABCD中,AF平分∠BAC,将矩形ABCD沿直线EF折叠,使点A、B分别落在边AD、BC上的点A'、B'处,连接A'B',然后展开,EF、A'F分别交AC于点G、H.若GH=2,HC=8,则BF的长为 ( )
A. B. C. D. 5
6. 如图,在△ABC中,点D在边AC上,AD∶DC=1∶2,O是BD的中点,连接AO并延长,交BC于点E,则BE∶EC等于 ( )
A. 1∶2 B. 1∶3
C. 1∶4 D. 2∶3
7. (2023·达州)如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器面板上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则支撑点C、D之间的距离为 cm(结果保留根号).
8. (2024·云南)如图,AB与CD交于点O,且AC∥BD.若=,则的值为 .
9. 在平面直角坐标系中,点A的坐标是(-2,1),以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为A'.若点A'恰在某一反比例函数的图像上,则该反比例函数的表达式为 .
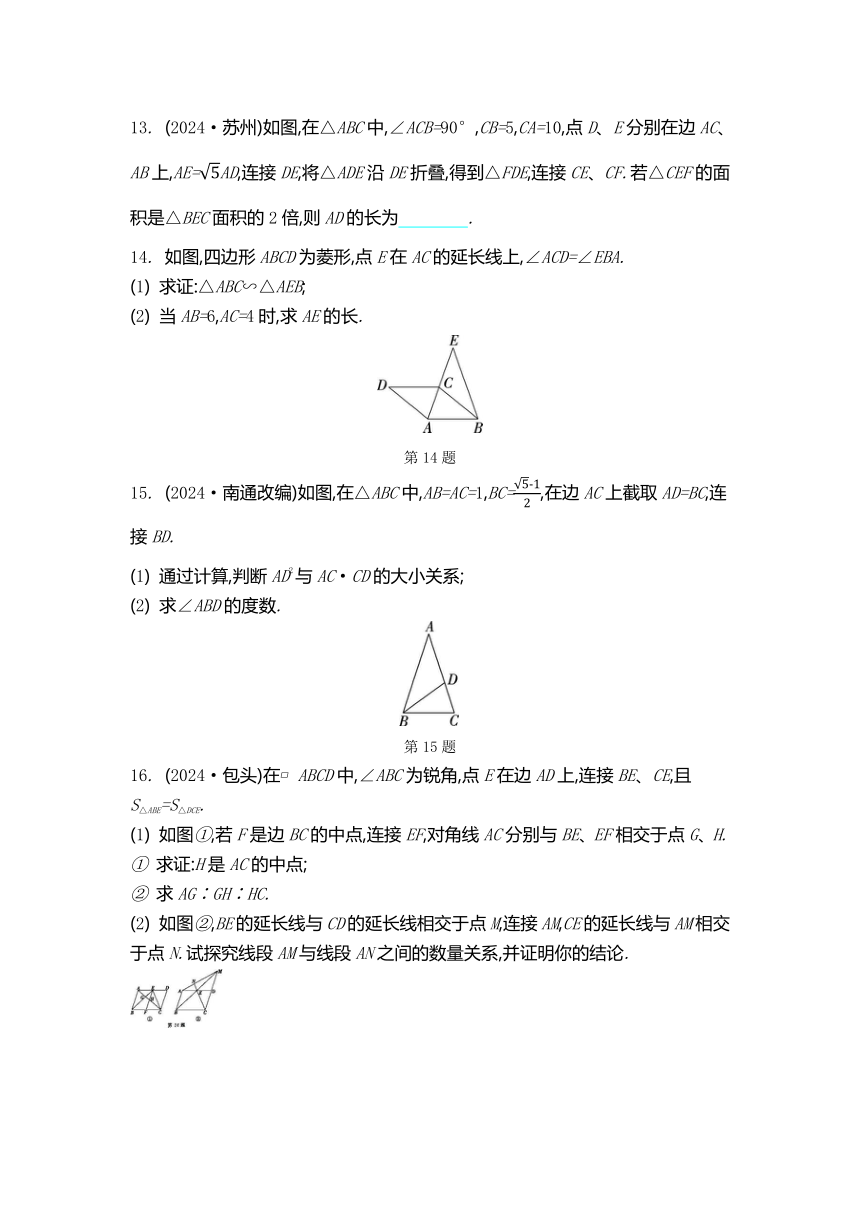
10. 如图,在正方形ABCD中,AB=12,AE=AB,点P在BC上运动(不与点B、C重合),过点P作PQ⊥EP,交CD于点Q,则CQ长的最大值为 .
11. 如图,△ABO的顶点A在函数y=(x>0)的图像上,∠ABO=90°,过AO的三等分点M、N分别作x轴的平行线,交AB于点P、Q.若四边形MNQP的面积为3,则k的值为 .
12. (2024·眉山)如图,菱形ABCD的边长为6,∠BAD=120°,过点D作DE⊥BC,交BC的延长线于点E,连接AE分别交BD、CD于点F、G,则FG的长为 .
13. (2024·苏州)如图,在△ABC中,∠ACB=90°,CB=5,CA=10,点D、E分别在边AC、AB上,AE=AD,连接DE,将△ADE沿DE折叠,得到△FDE,连接CE、CF.若△CEF的面积是△BEC面积的2倍,则AD的长为 .
14. 如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠EBA.
(1) 求证:△ABC∽△AEB;
(2) 当AB=6,AC=4时,求AE的长.
第14题
15. (2024·南通改编)如图,在△ABC中,AB=AC=1,BC=,在边AC上截取AD=BC,连接BD.
(1) 通过计算,判断AD2与AC·CD的大小关系;
(2) 求∠ABD的度数.
第15题
16. (2024·包头)在 ABCD中,∠ABC为锐角,点E在边AD上,连接BE、CE,且S△ABE=S△DCE.
(1) 如图①,若F是边BC的中点,连接EF,对角线AC分别与BE、EF相交于点G、H.
① 求证:H是AC的中点;
② 求AG∶GH∶HC.
(2) 如图②,BE的延长线与CD的延长线相交于点M,连接AM,CE的延长线与AM相交于点N.试探究线段AM与线段AN之间的数量关系,并证明你的结论.
17. (2024·威海)如图,AB是☉O的直径,点C、D在☉O上,且BC=CD.E是线段AB的延长线上一点,连接EC并延长,交射线AD于点F.∠FEG的平分线EH交射线AC于点H,∠H=45°.
(1) 求证:EF是☉O的切线;
(2) 若BE=2,CE=4,求AF的长.
第17题
18. 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标是(5,2),P是边CB上一动点(不与点C、B重合),连接OP、AP,过点O作射线OE,交AP的延长线于点E,交边CB于点M,且∠AOP=∠COM,令CP=x,MP=y.
(1) 当x为何值时,OP⊥AP
(2) 求y与x之间的函数表达式,并写出x的取值范围.
(3) 在点P运动的过程中,是否存在x,使△OCM与△ABP的面积之和等于△EMP的面积 若存在,请求出x的值;若不存在,请说明理由.
第18题
专题(二) 图形的相似
1. C 2. B 3. C 4. C 5. A 6. B
7. (80-160) 解析:∵ C是靠近点B的黄金分割点,AB=80cm,∴ AC=AB=×80=(40-40)cm.同理,可得DB=(40-40)cm.∴ CD=AC+BD-AB=2×(40-40)-80=(80-160)cm.
8. 9. y=- 10. 4 11. 18 12.
13. 解析:∵ AE=AD,∴ 可设AD=x,则AE=x.由折叠,得DF=AD=x,∠ADE=∠FDE.如图,过点E作EH⊥AC于点H,设EF与AC相交于点M,则易得△AHE∽△ACB.∴ ==.∵ CB=5,CA=10,∴ 在Rt△ABC中,AB===5.∴ ==.∴ EH=x,AH=2x.∴ DH=AH-AD=x=EH.∴ △EHD是等腰直角三角形.∴ ∠HDE=∠HED=45°.∴ ∠FDE=∠ADE=135°.∴ ∠FDM=135°-45°=90°.易得△FDM≌△EHM.∴ DM=MH=x.∴ CM=AC-AD-DM=10-x.∴ S△CEF=S△CME+ S△CMF=CM·(EH+DF)=10-x·2x=10x-x2.又∵ S△CEF=2S△BEC,S△BEC=S△ABC-S△AEC=×10×5-×10x=25-5x,∴ 10x-x2=2(25-5x).整理,得3x2-40x+100=0,解得x1=,x2=10(不合题意,舍去).∴ AD=.
14. (1)∵ 四边形ABCD为菱形,∴ ∠ACD=∠BCA.∵ ∠ACD=∠EBA,∴ ∠BCA=∠EBA.∵ ∠BAC=∠EAB,∴ △ABC∽△AEB (2) ∵ △ABC∽△AEB,∴ =.∵ AB=6,AC=4,∴ =.∴ AE=9
15. (1) ∵ BC=,AD=BC,∴ AD=.∵ AB=AC=1,∴ CD=1-=.∴ AD2==,AC·CD=1×=.∴ AD2=AC·CD (2) ∵ AD=BC,AD2=AC·CD,∴ BC2=AC·CD,即=.又∵ ∠C=∠C,∴ △BCD∽△ACB.∴ =,∠BDC=∠ABC,∠DBC=∠A.又∵ AB=AC,∴ ∠ABC=∠C.∴ ∠C=∠BDC.∴ BC=BD=AD.∴ ∠ABD=∠A=∠DBC.设∠ABD=x,则∠A=∠DBC=x.∴ ∠ABC=∠ABD+∠DBC=2x.∴ ∠C=2x.∵ 在△ABC中,∠A+∠ABC+∠C=180°,∴ x+2x+2x=180°,解得x=36°.∴ ∠ABD=36°
16. (1) ① ∵ 四边形ABCD是平行四边形,∴ AD∥BC,AD=BC.∴ ∠EAH=∠FCH.∵ S△ABE=S△DCE,∴ 易得AE=DE=AD.∵ F是BC的中点,∴ CF=BC.∴ CF=AE.∵ ∠AHE=∠CHF,∴ △AEH≌△CFH.∴ AH=CH.∴ H是AC的中点 ② ∵ ∠EAH=∠FCH,∠AGE=∠CGB,∴ △AGE∽△CGB.∴ =.∴ ==.设AG=2a,则CG=4a,∴ AC=AG+CG=6a.∴ AH=CH=3a.∴ GH=AH-AG=a.∴ AG∶GH∶HC=2a∶a∶3a=2∶1∶3 (2) AM=3AN 如图,过点M作MQ∥BC,交CN的延长线于点Q.∵ 在 ABCD中,AD∥CB,即ED∥BC,∴ △MED∽△MBC.∴ =.∴ ==.∴ EM=BM=BE.∵ MQ∥BC,∴ ∠MQE=∠BCE.∵ ∠MEQ=∠BEC,EM=EB,∴ △MQE≌△BCE.∴ MQ=BC.∴ MQ=AD.∵ MQ∥BC,AD∥CB,∴ MQ∥AD.∴ ∠MQE=∠AEN.∵ ∠MNQ=∠ANE,∴ △MQN∽△AEN.∴ =.∴ ==2.∴ MN=2AN.∴ AM=MN+AN=3AN
17. (1) 连接OC.∵ OA=OC,∴ ∠OAC=∠OCA.∵ BC=CD,∴ ∠DAC=∠BAC=∠BAF.∴ ∠OCA=∠DAC.∴ OC∥AF.∴ ∠OCE=∠F.∵ EH平分∠FEG,∴ ∠FEG=2∠GEH.∵ ∠GEH=∠H+∠BAC,∠FEG=∠F+∠BAF,∴ 2∠H+2∠BAC=∠F+∠BAF.∵ ∠BAF=2∠BAC,∴ ∠F=2∠H=90°.∴ ∠OCE=90°,即OC⊥EF.∵ OC是☉O的半径,∴ EF是☉O的切线 (2) ∵ AB是☉O的直径,∴ ∠ACB=90°.∴ ∠OBC+∠BAC=90°.∵ ∠OCE=90°,∴ ∠OCB+∠BCE=90°.∵ OB=OC,∴ ∠OBC=∠OCB.∴ ∠BCE=∠CAE.∵ ∠CEB=∠AEC,∴ △BCE∽△CAE.∴ ====.∴ CE2=BE·AE,即16=2AE,解得AE=8.∴ AB=8-2=6.∵ 在Rt△ABC中,AB=6,=,∴ AC=.∵ ∠F=∠ACB=90°,∠FAC=∠CAB,∴ △FAC∽△CAB.∴ =.∴ AF==
18. (1) 根据题意,知OA=CB=5,AB=OC=2,∠B=∠OCM=90°,BC∥OA.若OP⊥AP,则∠OPC+∠APB=∠APB+∠PAB=90°.∴ ∠OPC=∠PAB.∴ △OPC∽△PAB.∴ =,即=,解得x1=4,x2=1.∵ BC∥OA,∴ ∠CPO=∠AOP.∵ ∠AOP=∠COM,∴ ∠COM=∠CPO.∵ ∠OCM=∠PCO,∴ △OCM∽△PCO.∴ =,即=.∴ y=x-.当x=1时,y=-3<0,∴ x=1不合题意,舍去.∴ 当x=4时,OP⊥AP (2) 由(1),知y=x-.∵ y>0,∴ x->0,易得x>2.又∵ x<5,∴ x的取值范围是2
1. 已知===k,则k的值是 ( )
A. -1 B. 2
C. -1或2 D. 无法确定
2. 如图,△ABC与△DEF位似,点O为位似中心,相似比为.若△ABC的周长为4,则△DEF的周长为 ( )
A. 4 B. 6 C. 9 D. 16
3. 如图,P为线段AB上一点,AD与BC相交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中的相似三角形有 ( )
A. 1对 B. 2对 C. 3对 D. 4对
4. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心、CA长为半径的☉C与AB交于点D,则AD的长为 ( )
A. B. C. D.
5. (2024·自贡)如图,在矩形ABCD中,AF平分∠BAC,将矩形ABCD沿直线EF折叠,使点A、B分别落在边AD、BC上的点A'、B'处,连接A'B',然后展开,EF、A'F分别交AC于点G、H.若GH=2,HC=8,则BF的长为 ( )
A. B. C. D. 5
6. 如图,在△ABC中,点D在边AC上,AD∶DC=1∶2,O是BD的中点,连接AO并延长,交BC于点E,则BE∶EC等于 ( )
A. 1∶2 B. 1∶3
C. 1∶4 D. 2∶3
7. (2023·达州)如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器面板上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则支撑点C、D之间的距离为 cm(结果保留根号).
8. (2024·云南)如图,AB与CD交于点O,且AC∥BD.若=,则的值为 .
9. 在平面直角坐标系中,点A的坐标是(-2,1),以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为A'.若点A'恰在某一反比例函数的图像上,则该反比例函数的表达式为 .
10. 如图,在正方形ABCD中,AB=12,AE=AB,点P在BC上运动(不与点B、C重合),过点P作PQ⊥EP,交CD于点Q,则CQ长的最大值为 .
11. 如图,△ABO的顶点A在函数y=(x>0)的图像上,∠ABO=90°,过AO的三等分点M、N分别作x轴的平行线,交AB于点P、Q.若四边形MNQP的面积为3,则k的值为 .
12. (2024·眉山)如图,菱形ABCD的边长为6,∠BAD=120°,过点D作DE⊥BC,交BC的延长线于点E,连接AE分别交BD、CD于点F、G,则FG的长为 .
13. (2024·苏州)如图,在△ABC中,∠ACB=90°,CB=5,CA=10,点D、E分别在边AC、AB上,AE=AD,连接DE,将△ADE沿DE折叠,得到△FDE,连接CE、CF.若△CEF的面积是△BEC面积的2倍,则AD的长为 .
14. 如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠EBA.
(1) 求证:△ABC∽△AEB;
(2) 当AB=6,AC=4时,求AE的长.
第14题
15. (2024·南通改编)如图,在△ABC中,AB=AC=1,BC=,在边AC上截取AD=BC,连接BD.
(1) 通过计算,判断AD2与AC·CD的大小关系;
(2) 求∠ABD的度数.
第15题
16. (2024·包头)在 ABCD中,∠ABC为锐角,点E在边AD上,连接BE、CE,且S△ABE=S△DCE.
(1) 如图①,若F是边BC的中点,连接EF,对角线AC分别与BE、EF相交于点G、H.
① 求证:H是AC的中点;
② 求AG∶GH∶HC.
(2) 如图②,BE的延长线与CD的延长线相交于点M,连接AM,CE的延长线与AM相交于点N.试探究线段AM与线段AN之间的数量关系,并证明你的结论.
17. (2024·威海)如图,AB是☉O的直径,点C、D在☉O上,且BC=CD.E是线段AB的延长线上一点,连接EC并延长,交射线AD于点F.∠FEG的平分线EH交射线AC于点H,∠H=45°.
(1) 求证:EF是☉O的切线;
(2) 若BE=2,CE=4,求AF的长.
第17题
18. 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标是(5,2),P是边CB上一动点(不与点C、B重合),连接OP、AP,过点O作射线OE,交AP的延长线于点E,交边CB于点M,且∠AOP=∠COM,令CP=x,MP=y.
(1) 当x为何值时,OP⊥AP
(2) 求y与x之间的函数表达式,并写出x的取值范围.
(3) 在点P运动的过程中,是否存在x,使△OCM与△ABP的面积之和等于△EMP的面积 若存在,请求出x的值;若不存在,请说明理由.
第18题
专题(二) 图形的相似
1. C 2. B 3. C 4. C 5. A 6. B
7. (80-160) 解析:∵ C是靠近点B的黄金分割点,AB=80cm,∴ AC=AB=×80=(40-40)cm.同理,可得DB=(40-40)cm.∴ CD=AC+BD-AB=2×(40-40)-80=(80-160)cm.
8. 9. y=- 10. 4 11. 18 12.
13. 解析:∵ AE=AD,∴ 可设AD=x,则AE=x.由折叠,得DF=AD=x,∠ADE=∠FDE.如图,过点E作EH⊥AC于点H,设EF与AC相交于点M,则易得△AHE∽△ACB.∴ ==.∵ CB=5,CA=10,∴ 在Rt△ABC中,AB===5.∴ ==.∴ EH=x,AH=2x.∴ DH=AH-AD=x=EH.∴ △EHD是等腰直角三角形.∴ ∠HDE=∠HED=45°.∴ ∠FDE=∠ADE=135°.∴ ∠FDM=135°-45°=90°.易得△FDM≌△EHM.∴ DM=MH=x.∴ CM=AC-AD-DM=10-x.∴ S△CEF=S△CME+ S△CMF=CM·(EH+DF)=10-x·2x=10x-x2.又∵ S△CEF=2S△BEC,S△BEC=S△ABC-S△AEC=×10×5-×10x=25-5x,∴ 10x-x2=2(25-5x).整理,得3x2-40x+100=0,解得x1=,x2=10(不合题意,舍去).∴ AD=.
14. (1)∵ 四边形ABCD为菱形,∴ ∠ACD=∠BCA.∵ ∠ACD=∠EBA,∴ ∠BCA=∠EBA.∵ ∠BAC=∠EAB,∴ △ABC∽△AEB (2) ∵ △ABC∽△AEB,∴ =.∵ AB=6,AC=4,∴ =.∴ AE=9
15. (1) ∵ BC=,AD=BC,∴ AD=.∵ AB=AC=1,∴ CD=1-=.∴ AD2==,AC·CD=1×=.∴ AD2=AC·CD (2) ∵ AD=BC,AD2=AC·CD,∴ BC2=AC·CD,即=.又∵ ∠C=∠C,∴ △BCD∽△ACB.∴ =,∠BDC=∠ABC,∠DBC=∠A.又∵ AB=AC,∴ ∠ABC=∠C.∴ ∠C=∠BDC.∴ BC=BD=AD.∴ ∠ABD=∠A=∠DBC.设∠ABD=x,则∠A=∠DBC=x.∴ ∠ABC=∠ABD+∠DBC=2x.∴ ∠C=2x.∵ 在△ABC中,∠A+∠ABC+∠C=180°,∴ x+2x+2x=180°,解得x=36°.∴ ∠ABD=36°
16. (1) ① ∵ 四边形ABCD是平行四边形,∴ AD∥BC,AD=BC.∴ ∠EAH=∠FCH.∵ S△ABE=S△DCE,∴ 易得AE=DE=AD.∵ F是BC的中点,∴ CF=BC.∴ CF=AE.∵ ∠AHE=∠CHF,∴ △AEH≌△CFH.∴ AH=CH.∴ H是AC的中点 ② ∵ ∠EAH=∠FCH,∠AGE=∠CGB,∴ △AGE∽△CGB.∴ =.∴ ==.设AG=2a,则CG=4a,∴ AC=AG+CG=6a.∴ AH=CH=3a.∴ GH=AH-AG=a.∴ AG∶GH∶HC=2a∶a∶3a=2∶1∶3 (2) AM=3AN 如图,过点M作MQ∥BC,交CN的延长线于点Q.∵ 在 ABCD中,AD∥CB,即ED∥BC,∴ △MED∽△MBC.∴ =.∴ ==.∴ EM=BM=BE.∵ MQ∥BC,∴ ∠MQE=∠BCE.∵ ∠MEQ=∠BEC,EM=EB,∴ △MQE≌△BCE.∴ MQ=BC.∴ MQ=AD.∵ MQ∥BC,AD∥CB,∴ MQ∥AD.∴ ∠MQE=∠AEN.∵ ∠MNQ=∠ANE,∴ △MQN∽△AEN.∴ =.∴ ==2.∴ MN=2AN.∴ AM=MN+AN=3AN
17. (1) 连接OC.∵ OA=OC,∴ ∠OAC=∠OCA.∵ BC=CD,∴ ∠DAC=∠BAC=∠BAF.∴ ∠OCA=∠DAC.∴ OC∥AF.∴ ∠OCE=∠F.∵ EH平分∠FEG,∴ ∠FEG=2∠GEH.∵ ∠GEH=∠H+∠BAC,∠FEG=∠F+∠BAF,∴ 2∠H+2∠BAC=∠F+∠BAF.∵ ∠BAF=2∠BAC,∴ ∠F=2∠H=90°.∴ ∠OCE=90°,即OC⊥EF.∵ OC是☉O的半径,∴ EF是☉O的切线 (2) ∵ AB是☉O的直径,∴ ∠ACB=90°.∴ ∠OBC+∠BAC=90°.∵ ∠OCE=90°,∴ ∠OCB+∠BCE=90°.∵ OB=OC,∴ ∠OBC=∠OCB.∴ ∠BCE=∠CAE.∵ ∠CEB=∠AEC,∴ △BCE∽△CAE.∴ ====.∴ CE2=BE·AE,即16=2AE,解得AE=8.∴ AB=8-2=6.∵ 在Rt△ABC中,AB=6,=,∴ AC=.∵ ∠F=∠ACB=90°,∠FAC=∠CAB,∴ △FAC∽△CAB.∴ =.∴ AF==
18. (1) 根据题意,知OA=CB=5,AB=OC=2,∠B=∠OCM=90°,BC∥OA.若OP⊥AP,则∠OPC+∠APB=∠APB+∠PAB=90°.∴ ∠OPC=∠PAB.∴ △OPC∽△PAB.∴ =,即=,解得x1=4,x2=1.∵ BC∥OA,∴ ∠CPO=∠AOP.∵ ∠AOP=∠COM,∴ ∠COM=∠CPO.∵ ∠OCM=∠PCO,∴ △OCM∽△PCO.∴ =,即=.∴ y=x-.当x=1时,y=-3<0,∴ x=1不合题意,舍去.∴ 当x=4时,OP⊥AP (2) 由(1),知y=x-.∵ y>0,∴ x->0,易得x>2.又∵ x<5,∴ x的取值范围是2
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
